Unit - 1
Fluid Properties
The substance that has a tendency to flow is called as fluid. Generally, fluid is defined as a substance which is capable of spreading and changing its shape, according to is surroundings, without offering internal resistance.
In fluid mechanics, fluid is defined on the basis of its behaviour under the application of external forces. A solid, when subjected to a shearing force, deforms until the internal shear resistance equals the externally applied stress.
Within elastic limits or removal of the external force, the formation disappears and solid comes to its original shape. When a small shearing force is applied externally to the fluid it starts deforming and continues to do as long as applied force exists.
On removal of the external force, the fluid does not come to its original position. On the basis of this property, fluid can be defined as a substance which deforms continuously when subjected to external shearing force. This continuous deformation of fluid is known as flow.
Types of Fluids
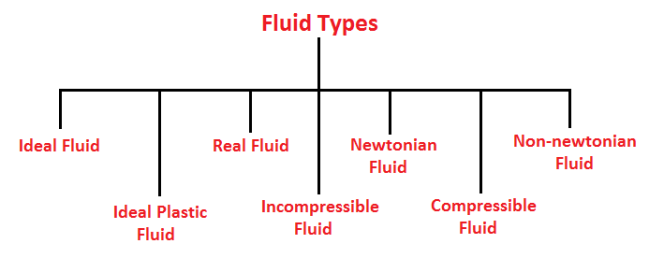
Based on how the property of viscosity of fluid changes in various fluids, they are divided into 5 types.
- Ideal fluid
- Real fluid
- Newtonian fluid
- Non-Newtonian fluid
- Ideal plastic fluid
- Incompressible fluid
- Compressible fluid
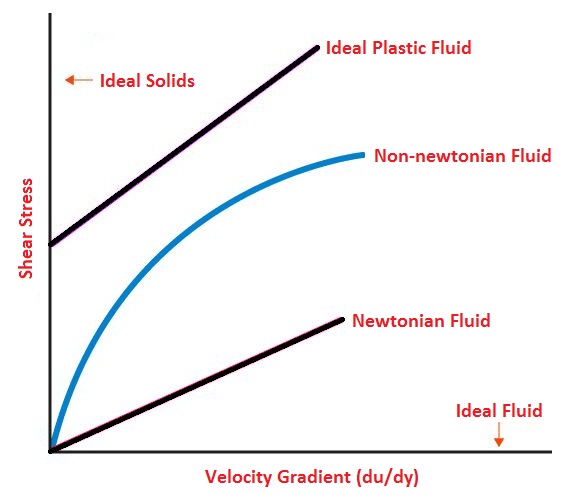
1) Ideal Fluid
The fluid, which is incompressible and has no viscosity or no friction, is known as an ideal fluid. Ideal fluid is only an imaginary fluid.
2) Real Fluid
A fluid, which possesses viscosity or friction, is known as real fluid.
3) Newtonian Fluid
A real fluid, in which the shear stress is directly proportional to the rate of the shear strain, is known as a Newtonian fluid. Fluids obeying Newton’s law where the value of viscosity (μ) is constant are known as Newtonian fluids.
4) Non-Newtonian Fluid
A real fluid, in which the shear stress is not proportional to the rate of the shear strain, is known as a Non-Newtonian fluid. Fluids in which the value of viscosity (μ) is not constant are known as non-Newtonian fluids.
5) Ideal Plastic Fluid
A fluid, in which the shear stress is more than the yield value and shear stress is proportional to the rate of shear strain, is known as ideal plastic fluid.
6) Incompressible Fluid
A fluid, in which the density of the fluid does not change which changes to an external force or pressure, is known as an incompressible fluid.
7) Compressible Fluid
A fluid, in which the density of fluid changes while the change in external pressure or force, is known as compressible fluid.
Graphical Representation of Fluids
Classifications of Fluid Flows
Some of the general categories of fluid flow problems are as follows;
1. Viscous and in viscid flow:
The fluid flow in which frictional effects become signification, are treated as viscous flow. When two fluid layers move relatively to each other, frictional force develops between them which is quantified by the fluid property ‘viscosity’. Boundary layer flows are the example viscous flow.
Neglecting the viscous terms in the governing equation, the flow can be treated as in viscid flow.
2. Internal and External flow:
The flow of an unbounded fluid over a surface is treated as ‘external flow’ and if the fluid is completely bounded by the surface, then it is called as ‘internal flow’.
For example, flow over a flat plate is considered as external flow and flow through a pipe/duct is internal flow. However, in special cases, if the duct is partially filled and there is free surface, then it is called as open channel flow. Internal flows are dominated by viscosity whereas the viscous effects are limited to boundary layers in the solid surface for external flows.
3. Compressible and Incompressible flow:
The flow is said to be ‘incompressible’ if the density remains nearly constant throughout. When the density variation during a flow is more than 5% then it is treated as ‘compressible’. This corresponds to a flow Mach number of 0.3 at room temperature.
Compressible fluid flow is defined as the flow in which the density is not constant which means the density of the fluid changes from point to point.
The density notation is ρ
ρ ≠ constant
Incompressible fluid flow is defined as the flow in which the density is constant which means the density of the fluid does not change from point to point.
ρ = constant
Gases are compressible fluid flow but whereas the liquid is incompressible fluid flow.
4. Laminar and Turbulent flow:
The highly ordered fluid motion characterized by smooth layers of fluid is called ‘Laminar Flow’, e.g. Flow of highly viscous fluids at low velocities.
The fluid motion that typically occurs at high velocities is characterized by velocity fluctuations are called as ‘turbulent.’ The flow that alternates between being laminar & turbulent is called ‘transitional’.
The dimensionless number i.e. Reynolds number is the key parameter that determines whether the flow is laminar or turbulent.
- If the Reynolds Number is less than 2000, the flow is called Laminar flow.
- Reynolds Number is more than 4000, the flow is called Turbulent flow.
- If the Reynolds Number is lies between 2000-4000, the flow may be laminar or turbulent.
5. Steady and Unsteady flow:
When there is no change in fluid property at point with time, then it implies as steady flow. However, the fluid property at a point can also vary with time which means the flow is unsteady/transient. The term ‘periodic’ refers to the kind of unsteady flows in which the flow oscillates about a steady mean.
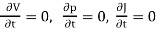(Steady Flow)
(Unsteady flow)
5. Natural and Forced flow:
In a forced flow, the fluid is forced to flow over a surface by external means such as a pump or a fan. In other case (natural flow), density difference is the driving factor of the fluid flow. Here, the buoyancy plays an important role. For example, a warmer fluid rises in a container due to density difference.
6. One/Two/Three dimensional flow: A flow field is best characterized by the velocity distribution, and thus can be treated as one/two/three dimensional flow if velocity varies in the respective directions.
One dimensional flow is that type of flow in which the flow parameter such as velocity is a function of time and one space co-ordinate only, say x.
u=f(x), v=0 and w=0
Where u v and w are velocity component in x,y and z directions respectively.
Two-dimensional fluid flow is the type of flow in which velocity is a function of time and two rectangular space co-ordinate say x,y
u= f1(x,y,), v= f2(x,y,) and w= 0.
Three-dimensional fluid flow is the type of flow in which velocity is a function of time and three mutually perpendicular directions. The function of 3 space coordinates (x,y,z).
u= f1(x,y,z), v= f2(x,y,z) and w= f3(x,y,z).
7. Uniform and non-uniform flow:
This uniform fluid flow is defined as the type of flow in which the velocity at any given time does not change with respect to space (i.e length of direction of the flow).
Uniform flow
Whereas the Non-uniform flow is defined as,
This non-uniform fluid flow is defined as the type of flow in which the velocity at any given time changes with respect to space (i.e. length of the direction of the flow).
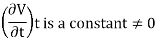
Non-uniform flow
8. Rotational and irrotational Fluid flow:
The rotational fluid flow is defined as the type of fluid flow in which the fluid particles while flowing along streamline and also rotate about their own axis.
Whereas, The Ir-rotational fluid flow is defined as the type of fluid flow in which the fluid particles while flowing along streamline and do not rotate about their own axis.
Key Takeaways:
- Boundary layer flows are the example viscous flow.
- Internal flows are dominated by viscosity whereas the viscous effects are limited to boundary layers in the solid surface for external flows.
- Gases are compressible fluid flow but whereas the liquid is incompressible fluid flow.
- The flow that alternates between being laminar & turbulent is called ‘transitional’.
It is defined as the ratio of mass of the fluid to its volume. Its unit is kg/m3 and its dimensional formula is ML-3.
Density depends on temperature and pressure.
- The specific weight of a fluid is defined as weight per unit volume at a standard temperature and pressure.
- It is denoted by 'w' or '
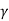' (gamma). It has S.I. Unit is N/m3. - Specific weight of water is 9810 N/m³ (9.81 kN/m³).
- γ =
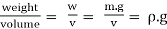
- ∴ γ = ρ.g
- The specific weight depends on gravitational acceleration and the mass density. Since gravitational attraction varies from place to place, the specific weight will also vary.
Key Takeaways:
The specific weight of a fluid is defined as weight per unit volume at a standard temperature and pressure.
- Specific gravity is the ratio of specific weight (or mass density) of fluid to the specific weight (or mass density) of a standard fluid.
- It is denoted by S or RD.
- Specific gravity =
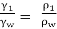
- For liquid, water and for gases, hydrogen or air is consider as a standard fluid.
- Specific gravity of water at a standard temperature 4°C is 1 and that of mercury is 13.6.
Key Takeaways:
Specific gravity is the ratio of specific weight (or mass density) of fluid to the specific weight (or mass density) of a standard fluid.
The ratio of shear stress to shear rate is a constant, for a given temperature and pressure, and is defined as the viscosity or coefficient of viscosity.
According to Newton’s law of viscosity the shear stress is directly proportional to rate of shear strain or rate of angular deformation or velocity gradient. The fluid which follows this is law is called Newtonian fluid.
τ α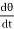 
τ = μ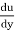
Newton’s law of viscosity is similar to Hooke’s law for solid.
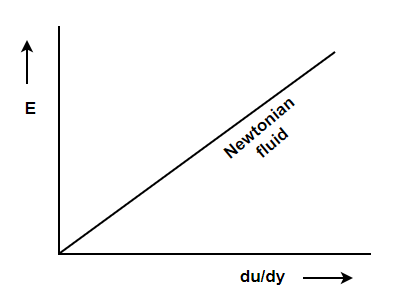
Figure: Diagram for newton’s law of viscosity
Examples:
Q.1 A skater weighing 1000 N attains a speed of 72 km/hour on ice, average skating area being 10 cm². The dynamic coefficient of friction between the Skater and ice may be taken as 0.015. Determine the average thickness of water. Layer existing between the skater and the skating surface. Viscosity of water at 0°C may be taken 1 x 10 N-s/m².
Soln.:
Given:
W=1000N,
u = 72 kmph = 72x=20m/sec,
A = 10 cm² = 10 x 10 m², -0.015, 10¹N-s/m²
To find: Average thickness.
Force responsible for motion = Frictional resistance
F = μN=pW
Where N= W
F= 0.015 x 1000 = 15 N
Newton's law of viscosity
F = τ.A =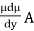 
15 = 1 ×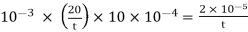 
t = 1.33 ×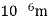 
Average thickness of water layer is 1.33 x 10 m
Q.2 A body weighing 1000 N slides down at a uniform speed of 1 m/s along a lubricated Inclined plane making 30° angle with the horizontal. The viscosity of lubricant is 0.1 kg/ms and contact area of the body is 0.25 m². Determine the lubricant thickness assuming linear velocity distribution. -June 2011. 6 Marks
Soln.:
Given:
W= 1000 N,
θ = 30°
Du = V = 1m/s,
A=0.25 m²
H=0.1 kgm/s 0.1x9.81 Nm/s = 0.981 Nm/s
To find: Lubricant thickness t
Shear force= Weight component along plane
= 1000 sin 30
F = 500 N
Shear stress
τ = 
By Newton's law of viscosity
τ = 
τ = 4.905 mm
The lubricant thickness is 4.905 mm.
Key takeaways
Newton's viscosity law states that the shear pressure between adjacent water layers is equal to the velocity gradients between these two layers.
Absolute viscosity - the coefficient of total viscosity - is the measure of internal resistance. Dynamic (absolute) viscosity is the tangential force at each unit area required to move one horizontal plane in relation to another plane - by unit velocity - while maintaining unit distance outside the fluid.
Shave pressure between layers of fluid in straight lines can be defined by Newtonian fluid as
Liquid - viscosity and velocity profile
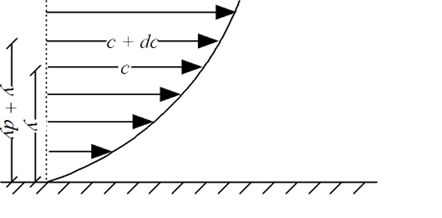
Fig: Dynamic and kinematic viscosity
Shear depression can be shown
τ = μ dc / dy
= μγ. ........ (1)
Where
τ = cutting pressure on liquid (N / m2)
μ = strong viscosity of liquid (N s / m2)
Dc = unit velocity (m / s)
Dy = unit distance between layers (m)
γ = dc / dy = shear rate (s-1)
Equation (1) is known as the Newtons Law of Friction.
(1) Can be rearranged to reflect Dynamic viscosity as
μ = τ dy / dc
= τ / γ. .......... . (1b)
- In the SI system the dynamic viscosity units are N s / m2, Pa s or kg / (m s) - where
1 Pa s = 1 N s / m2 = 1 kg / (m s) = 0.67197 lbm / (ft s) = 0.67197 slug / (ft s) = 0.02089 lbf s / ft2
- Strong viscosity can also be expressed in the metric CGS system (centimeter-gram-second) such as g / (cm s), dyne s / cm2 or poise (p) where
1 poise = 1 dyne s / cm2 = 1 g / (cm s) = 1/10 Pa s = 1/10 N s / m2
- Effective use Poise is usually very large and the unit is therefore divided by 100 - into a small centipoise (cP) unit - where
1 P = 100 cP
1 cP = 0.01 poise = 0.01 gram per cm second = 0.001 second Pascal = 1 milliPascal second = 0.001 N s / m2
20.2oC (68.4oF) liquids have a perfect viscosity of one - 1 –centiPoise.
Examples:
Q.1 A plate 0.02 mm distance from a fixed plate, moves at 60 cmvs and requires a force of 3 N/m² to maintain this speed. Determine the fluid viscosity between the plates.
Soln.:
Given: Distance between plates
Dy= 0.02 mm = 0.02 x 10-3 m
Velocity of upper plate u 60 cm/s 0.6 m/s
Change in velocity du=u-0-0.6 m/s.
τ = Force per unit Area = 3 N/m²
To find: Viscosity
Using Newton's law of viscosity
τ =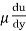 
3 = μ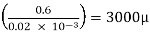
μ = 1×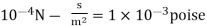
The fluid viscosity between the plates is 1 x 
poise,
Q.2 A flat plate of area 2.5 x 10 mm² is pulled with a speed of 0.4m's relative to another plate locate at a distance of 0.15mm from it. Find the force and power required to maintain this speed, if the fluid separating them is having viscosity as 1 poise
Soln.:
Given:
A=2.5 x 10 mm²=2.5m²,
Du= 0.4m/s dy-0.15mm = 0.15 x 10 m,
μ =1 poise = 0.1N-s/m
To find: Force, power
Using Newton's law of viscosity:
τ = μ
τ = 0.1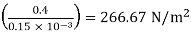
μ = 1 × 
As we known τ = 
F = 266.67 × 2.5 = 666.67 N
Power required to move the plate at speed 0.4 m/s
= Force x Velocity = 666.67 x 0.4 N-m/
1 N-m/s = 1 Watt
P = 266.67 Watt
Power required moving the plate is 266.67 Watt.
Q.3 The space between two square flat parallel plates is filled with oil. Each side of the plate is 720 mm. The thickness of the oil film is 15 mm. The upper plate, which moves at 3 ms requires a force of 120 N to maintain the speed. May 2016. 6 Marks
Determine:
(1) The dynamic viscosity of oil.
(2) The kinematic viscosity of oil if the specific gravity of oil is 0.95
Solution:
Square plate of side, a = 720 mm=0.72 m
Thickness of oil film, t = 15 mm= 15 x 10
Velocity of plate v= du= 3m/s
Force F= 120 N
Specific gravity s= 0.95
To find μ = v
Mass density,
ρ = s × ρwater
= 0.95 × 1000 = 
Area of plate,
A= 0.72x0.72 = 0. 5184 m²
Using Newton's law viscosity
τ = μ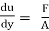
μ × 
Dynamic viscosity μ = 1.157 N/m²
Kinematic viscosity, v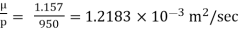
Q. 4 A body with gravity force of 500 N with a flat surface area 0.2 m slides down a lubricated inclined plane making a 30° angle with the horizontal. For viscosity of 0.1 kg s/m and body speed of 1 m/s. Determine the lubricant film thickness
Soln.:
Given:
Area A = 0.2 m²
Weight of late W = 500 N
Velocity of plate u = 1 m/sec 0.1kg /m²=0.1 x 9.81 N.s/m² = 0.981 N-s/m²
To find: Thickness of film.
Component of W along the plate W sin 8= 500 sin 30= 250 N
Shear force on the bottom surface of the plate
F = 250N
τ =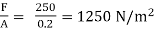 
τ = 
1250 = 0.981 ×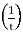 
τ = 0.785 ×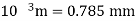 
The lubricant film thickness is 0.785 mm
Q.5 A rectangular plate 1.2 m x 0.4 m. Weighting 970N slides down a 45° inclined surface at a uniform velocity of 2.25 m/s. If the 2mm gap between the plate and the inclined surface is filled with oil, determine the viscosity of oil.
Soln.:
Given:
Area A = 12x04 0.48 m²
Weight of plate W =970 N
Velocity of plate u = 2.25 m/sec
Thickness of film t = dy = 2 mm = 2 x 10³ m
To find: Viscosity
Component of W along the plate= W sin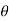 
970 sin 45 = 685.97 N
Shear force on the bottom surface of the plate
F= 685.89 N
t =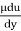 
1428.94 = μ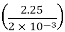
μ = 1.27 N -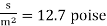 
The viscosity of the liquid is 12.7 poise.
Key takeaways
Dynamic viscosity
Absolute viscosity - the coefficient of total viscosity - is the measure of internal resistance. Dynamic (absolute) viscosity is the tangential force at each unit area required to move one horizontal plane in relation to another plane - by unit velocity - while maintaining unit distance outside the fluid.
Stokes Theorem (additionally called Generalized Stoke’s Theorem) is a assertion approximately the combination of differential bureaucracy on manifolds, which each generalizes and simplifies numerous theorems from vector calculus. As in keeping with this theorem, a line crucial is associated with a floor crucial of vector fields. Learn the stokes regulation right here in element with system and proof.
The Stoke’s theorem states that “the floor vital of the curl of a feature over a floor bounded with the aid of using a closed floor is same to the road vital of the unique vector feature round that floor.”
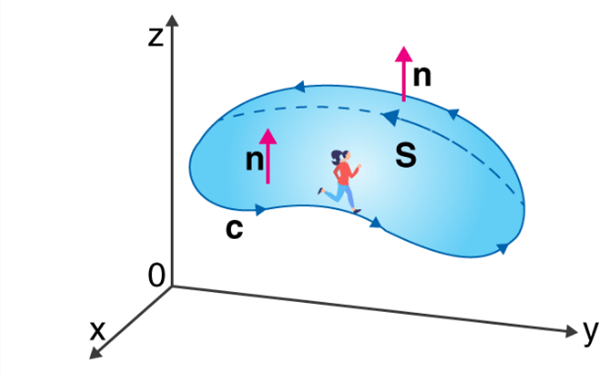
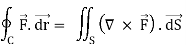
Where,
C = A closed curve.
S = Any surface bounded by C.
F = A vector field whose components have continuous derivatives in an open region of R3 containing S.
This classical declaration, along with the classical divergence theorem, fundamental theorem of calculus, and Green’s theorem are exceptional cases of the general formulation specified above.
Stokes Theorem Proof:
We count on that the equation of S is Z = g(x, y), (x, y)D
Where g has a non-stop second-order partial derivative.
D is an easy undeniable place whose boundary curve C1 corresponds to C.
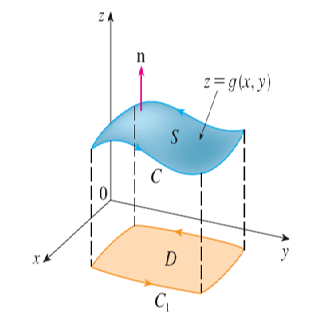
Example:
Using stokes theorem, evaluate 
Solution:
Given,
Equation of sphere: x2 + y2 + z2 = 4….(i)
Equation of cylinder: x2 + y2 = 1….(ii)
Subtracting (ii) from (i),
z2 = 3
z = √3 (since z is positive)
Now,
The circle C is will be: x2 + y2 = 1, z = √3
The vector form of C is given by:
r(t) = cos t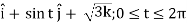 
Thus, r’(t) = -sin t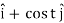
Let us write F(r(t)) as:
F(r(t)) = √3 cos t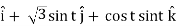 
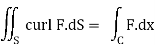
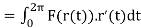
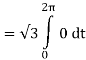
= 0
Key Takeaways:
The Stoke’s theorem states that “the floor vital of the curl of a feature over a floor bounded with the aid of using a closed floor is same to the road vital of the unique vector feature round that floor.”
- The surface tension of a liquid is the property by which a fluid is enables to resist tensile stress.
- It is due to the cohesion between the molecules at the surface of a liquid. It is the force required to maintained unit length of the film in equilibrium. It is denoted by '' (sigma). S.I. Unit = N/m.
- All liquid molecules have tendency to attract each other.
- A liquid molecule on the interior of the liquid body has other molecules on all side of its, so that the forces of attraction are in equilibrium and the molecule is equally attracted on all sides, as a molecule at point A as shown in Fig.
- A liquid molecule at the free surface at point B, does not have liquid molecule above it to pull them outward, so that the free surface molecule tries to move towards the center by downward force.
- This force on the liquid surface is normal to the liquid surface. A film or layer is occurring on the liquid surface which is in tension and resist small loads if placed gently over it.
- It occurs at the interface of a liquid and a gas or at the interface of two liquids and is essentially due to intermolecular forces of cohesion.
- As the temperature increases, the surface tension is decreases.
- A small needle placed gently upon the water surface will not sink but will be supported by the tension at the water surface.
- The effect of surface tension is to reduce the surface of a free body of liquid to a minimum. That is why falling drops of rain become spherical shape.
- Surface tension force can be reduced by the addition of detergents. Surface tension value of liquids when it is cannot with air
= 0.073 N/m for air-water interface
= 0.480 N/m for air-mercury interface
- Surface tension leads to the phenomena of capillary waves on a liquid surface and capillary rise or depression.
Pressure Intensity Inside a Droplet:
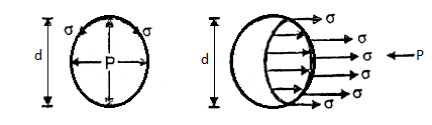
- Consider a spherical droplet of diameter 'd'. Let the excess pressure developed inside the droplet 'P' and ' ' is the surface tension in the surface of droplet as shown in Fig.
- For static equilibrium condition
Surface tension force = Force due to excess pressure
Surface tension x Circumference = Excess pressure x Normal area
σ(πd) = P(
∴ P =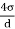 
- Thus, pressure intensity inside a droplet varies inversely with the diameter. Pressure intensity decreases with an increase in the size of the droplet.
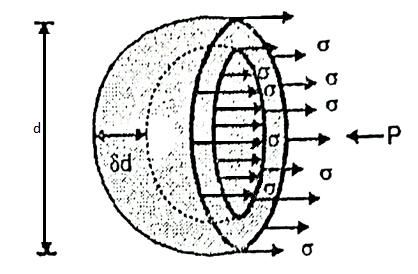
Pressure Intensity Inside a Soap Bubble:
- Soap bubble has two surfaces in contact with air, inside and outside.
- Consider a soap bubble of external diameter d and thickness of bubble=
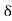d as shown in Fig.
= Surface tension on inner surface
= Surface tension on outer surface
- For static equilibrium,
Force due to excess pressure = Force due to surface tension
Excess pressure x Normal area= Surface tension x Circumference
P ×
p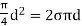
∴P =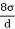 
- Thus, excess pressure inside the soap bubble is twice as that of droplet.
Pressure Intensity Inside a Liquid Jet:
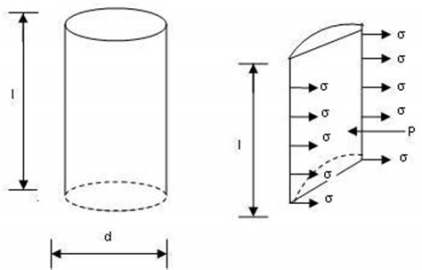
- Consider a liquid jet as a cylinder of diameter ‘d’ and length ‘l’ as shown in fig.
- Force due to excess pressure = Force due to surface tension
- Excess pressure x Normal area = Surface tension x Circumference
P(d×L) = σ(2L)
∴ P =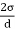 
Application of Surface Tension:
- Formation of droplets.
- Ability of needle to float on water.
- Falling drop become spherical shape.
Key Takeaways:
The surface tension of a liquid is the property by which a fluid is enables to resist tensile stress.
Examples:
Q.1 Calculate the gauge pressure and the absolute pressure within:
(1) a droplet of water 0.3 cm in diameter
(2) a jet of water 0.3 cm in diameter.
Assume the surface tension of water as 0.07 N/m and atmospheric pressure as 101.3 N/m² Dec. 2010, 4 Marks
Soln.:
Given:
d = 3mm = 3 x 10³ m.
σwater = 0.073N/m.
Patm = 101.3 N/m² atm
For droplet and air bubble
P =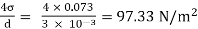 
Absolute pressure. (P) = Pgauge + Patm = 97.33 + 101.3 = 198.63 N/m²
For jet
P =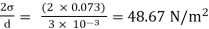 
Absolute pressure in jet
Pabs + Patm = 48.67 + 101.3 = 149.97 N/m2
Q.2 Determine the diameter of a droplet of water in mm it t pressure inside is to be greater than that outside by 13 Nm². Take a 7.26 10 Nm.
Soln.:
Given:
P-130 N/m²
σ= 7.26×10^-2 N/m
For droplet, P
P =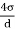 
d =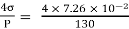 
= 2.33 mm
The diameter of a droplet of water is 2.33 mm
Q.3 In the surface tension at air water interface is 0.070 Nm what is the pressure difference between inside and outside of an air bubble of diameter of 0.01 mm?
Soln.:
Given: -
= 0.07 Nm.
D= 001mm= 0.01 = 10 m
An air bubble has only one surface,
P = 
The pressure difference between inside and outside of an air bubble is P= 25000N/m2
Q.4 Calculate the pressure inside a soap bubble of 50mm diameter. Take surface tension at the soap air interface as 0.1Nm
Soln.:
Given:
= 0.1Nm,
d=50x10^-3 mm
For soup bubble, P
P = 
The pressure inside a soup babble is 16 N/m2
Q.5 If the surface tension at air water interface is 0.075 N/m, what is the pressure difference between inside and outside of an air bubble of diameter of 0.01 mm?
Soln.:
Given:
water = 0.075N/m,
d=0.01mm
An air bubble has only one surface,
P =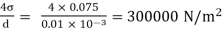 
The pressure difference between inside and outside of an air bubble is P=30000N/m2
Q.6 What force is necessary to it a thin platinum wire ring of negligible thickness having 5 cm diameter from a water surface? Neglect weight of wire and consider surface tension of water as 0.0725 Nm.
Soln.:
Given: -
= 0.0725 N/m,
D= 5 cm = 0.05m
Force required to lift a than wire ring
F = πdσ = π × 0.05 × 0.072 = 0.0113 N
Key takeaways
Surface tension is the tendency for the liquid to shrink into the smallest possible area. Facial friction allows insects (e.g. Water arrows), to float and slide on the surface of water without immersion.
Where fluids combine with air, the resulting incompatibility arises from the greater attraction of liquid molecules to each other (due to bonding) than to air molecules (due to adhesion).
There are two main processes in play. One is the internal energy of the extra molecules that make the liquid enter. The second is the gravitational force associated with the surface of the membrane. The effect of the net is that the liquid behaves as if its surface was covered with a thick membrane.
- When a small diameter tube less than 6 mm is inserted vertically inside a pool of liquid, the liquid level in the tube either rise or falls relatively to the liquid level in the pool.
- This phenomenon of rise or fall of liquid level in the capillary tube is called as capillarity. Capillary is due to cohesion and adhesion.
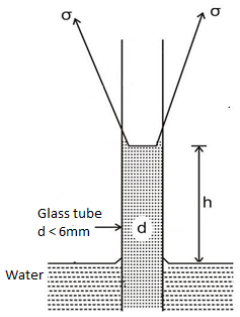
Fig: Capillary rise
- If the adhesion force between molecules of liquid and tube is more than cohesion between liquid molecules (e.g., water), the liquid will wet the glass surface and the liquid level will rise.
- The liquid level will become concave upward as shown in Fig.
- In such case angle between surface tension with the vertical (θ) is less than 90°.
- If cohesive force between molecules of liquid and tube is more than cohesion between liquid molecules (If cohesive force predominate)
- E.g., mercury, the liquid does not wet the surface, liquid level will fall as shown in Fig.
- The liquid became convex upwards in such case angle between surface tension with the vertical (θ) is greater than 90°
- E.g., suction of kerosene in lamp, rise of water in soil are example of capillarity
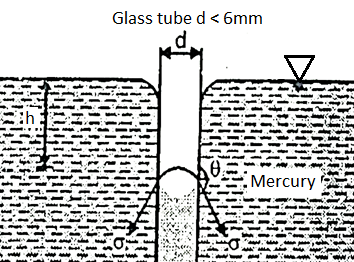
Fig: Capillary fall
Expression for Capillary Rise:
- Let h be the capillary rise or fall in a tube of diameter 'd' centre surface tension force in upward direction.
P = πdσ cos θ
Weight of liquid column
= V.γ =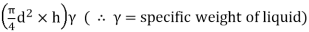 
- Under equilibrium, the weight of liquid column will be balanced by surface tension force ' '.
Weight of liquid = Surface tension force
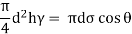
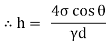
- For pure water in contact with clean glass and air, θ = 0
h =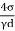 
- For mercury and glass, θ = 140°
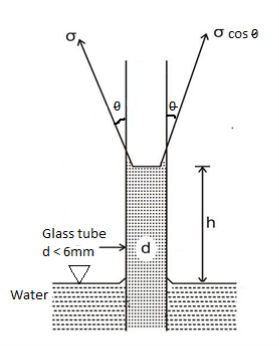
Fig: Capillary rise
- Capillary rise Capillary rise in a gap between two closed spaced parallel plate
h =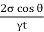 
Where 't' is the gap between the plates.
Application of Capillarity:
- Capillarity action is responsible for moving ground water from wet areas of the soil to dry areas.
- Suction of kerosene in lamp.
Key Takeaways:
When a small diameter tube less than 6 mm is inserted vertically inside a pool of liquid, the liquid level in the tube either rise or falls relatively to the liquid level in the pool. This phenomenon of rise or fall of liquid level in the capillary tube is called as capillarity. Capillary is due to cohesion and adhesion.
Compression is an asset to be reduced to a minimum by pressure. This material is the result of porosity, and the change in mass occurs from particles that come close together by pressure.
Liquid pressure is actually a measure of the change in the quantity that will be produced in a liquid by a certain change. Gases, in general, are highly compressed and most liquids have very low pressures.
The fact that the effects of stress can have a profound effect on the flow of fluid. The study of this flow when changes in quantity and temperature are most important is what is known as compressible flow fluid or gas dynamics.
Examples:
Q.1 A pressure of 1.2 M Pascal is applied to 350 liters of liquid, causes a volume reduction of 1.5 liters. Calculate bulk modulus of elasticity for the liquid also find the compressibility.
Soln.:
Given:
Pressure p= 1.2M,
Pascal = 12x10 N/m².
Volume V 650 liter= 650 x 10³ m.
Reduction in volume dV= 1.5 liter= 1.5 x 10^-3 m3
Bulk modulus of elasticity, K
k =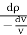 
k =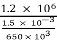 
k = 520 × 106 N/m2
Compressibility
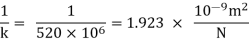
The Bulk modulus of elasticity for the liquid is 520 M Pa and compressibility is 1.923 x 10 m/N.
Q.2 At a depth of 5 kilo meters in the ocean the pressure 480 kg/cm Assuming specific weight at the surface as is 1025 kgm and that the average modulus of elasticity is 24 x 10 kg/cm for that pressure range. Calculate:
a) The change in specific volume between the surface and the given depth
b) Specific volume at the given depth and
c) Specific weight at that depth.
Soln.:
Given:
Pressure dp = 480 kg/cm²
Average modulus of elasticity K = 24 x 10' kg/cm
k = 
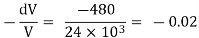
Specific volume of the water at the surface of the ocean,
Specific volume
v = 
DV = 
Specific volume at the depth of 5 km,
VS =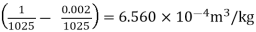 
Specific weight of water at the depth of 5 km,
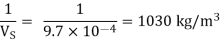
Q.3 At a depth of 2 km in an ocean, the pressure is 840 bar. Assume the specific weight at surface as 10,250 N per m² and the average Bulk modulus of elasticity as 2.4 x 10° kN per sq.m. For that pressure range.
1) What will be the change in specific volumes between that at the surface and at that depth?
2) What will be the specific volume at that depth?
3) What will be the specific weight at that depth?
Soln.:
Given:
P₁ = 840 x 10¹ Pa,
H1, = 2 km = 2000 m.
γ0= 10250 N/m²,
K = 2.4 x 10' Pa
Bulk modulus K
k =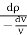 
And ρ0 =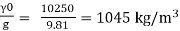 
Specific volume
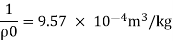
2.4×109 =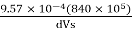 
Change in specific volume
DVs = 3.3498×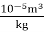
Specific volume at 2 km depth
VS – dVS = 9.235× 10-4 m3/kg
Density at 2 km depth
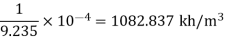
Specific weight
γ = 1082.837 × 9.81 = 10622.6 N/m3
Key takeaways
Compression is an asset to be reduced to a minimum by pressure. This material is the result of porosity, and the change in mass occurs from particles that come close together by pressure.
Vapour pressure is a measure of the tendency of a material to change into the gaseous or vapour state, and it increases with temperature. The temperature at which the vapour pressure at the surface of a liquid becomes equal to the pressure exerted by the surroundings is called the boiling point of the liquid.
P solution = X solvent P solvent
P solution = vapor pressure of the solution
X solvent = mole fraction of the solvent
Psolvent = vapor pressure of the pure solvent
Key Takeaways
Vapour pressure is a measure of the tendency of a material to change into the gaseous or vapour state, and it increases with temperature.
It is reciprocal of Bulk modulus (K)
ß=1/K
Bulk Modulus is defined as the ratio of compressive stress to volumetric strain.
K=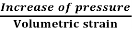 
K = (dp)/(-dv/V)
-ve sign means the volume decrease with increase in pressure.
We know that, ρ = 
Since, R= Characteristics gas constant and T is constant (isothermal process).
Differentiating the above equation
(dp/dρ) = RT
Now the isothermal bulk modulus
KT=.(dp/d)= . RT=P
KT=P
- Kinematics of fluid float offers with the movement of fluid debris without thinking about the corporation generating the movement. This offers with the geometry of movement of fluid debris.
- This additionally offers with the rate and acceleration of fluid debris in movement. The movement of a fluid may be analysed at the equal ideas as the ones carried out with inside the movement of a stable.
- There, but exists a fundamental distinction among the movement of a stable and the movement of a fluid. A stable frame is compact and movements as one mass.
- Hence, we take a look at the movement of the complete frame and there's no necessity to take a look at the movement of any particle of a stable frame.
Methods of Describing Fluid Motion:
We recognize that every particle of a fluid in movement has at any on the spontaneous a positive exact cost of its residences like density, velocity, acceleration etc. As the fluid movements on, the values of those residences will extrude from one function to different positions, from time to time.
Thus, it could be found out that techniques are feasible to explain fluid movement. In the primary approach known as the Lagrangian approach, we have a look at the velocity, acceleration etc. of acharacter fluid particle at each on the spontaneous of time because the particle movements to distinctive positions.
This approach of reading the residences of an unmarried fluid particle is a completely tedious procedure and consequently this approach isn't always typically adopted.
In the second one approach known as the Eulerian approach, we describe the waft via way of means of reading the velocity, acceleration, pressure, density etc. at a set factor in space. Due to its smooth application, this approach is maximum typically adopted.
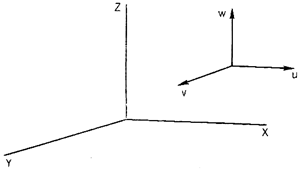
Let x, y and z denote the space coordinates and t the time. Let V be the resultant velocity at any point in space in a fluid body. Let u, v and w be the components of the resultant velocity V at any point in the directions of the x, y and z axes. Fig illustrates the notations.
In the Eulerian method the velocity at a point (x,y,z) can be expressed as
u = f1 (x, y, z, t)
v = f2 (x, y, z, t)
w = f3 (x, y, z, t)
V = f4 (x, y, z, t)
Relation (i) can be explained as follows. The velocity component u is some function of the space coordinates x,y,z. Hence for certain values of x,y, z and t there is a corresponding value of u.
Stream Line:
A circulate line is a non-stop line in a fluid which indicates the course of the speed of the fluid at every factor alongside the line. The tangent to the circulate line at any factor on it's far with inside the course of the speed at that factor. Fluid debris mendacity on a circulate line at an on the spontaneous circulate alongside the circulate line.
Hence, there may be no alternate with inside the course of the speed vector at a factor. In different words, the circulate line is constant in function. Conversely, if the circulate line sample stays regular the float is steady. In the case of an unsteady float, the course of the speed modifications with time at each factor. This method the placement of a circulate line isn't always regular.
Path Line:
A course line way the course or a line simply defined via way of means of a unmarried fluid particle because it movements all through a duration of time. The course line suggests the route of the rate of the identical fluid particle at successive instants of time. In the case of a constant waft given that there aren't any any fluctuations of the rate, the course line coincides with the move line.
Stream Tube:
It is a meeting or series of circulate strains forming a tabular area. The floor of a circulate tube is made of circulate strains. The pace of a fluid particle at the floor of the circulate tube is alongside the circulate line over the floor of the circulate tube.
Key Takeaways:
- A stable frame is compact and movements as one mass.
- This approach of reading the residences of a unmarried fluid particle is a completely tedious procedure and consequently this approach isn't always typically adopted.
- Fluid debris mendacity on a circulate line at an on the spontaneous circulate alongside the circulate line.
- This method the placement of a circulate line isn't always regular.
- The pace of a fluid particle at the floor of the circulate tube is alongside the circulate line over the floor of the circulate tube.
Steady and Unsteady flows
Steady flow – The type of flow in which the fluid characteristics like velocity, pressure, density, etc. at a point do not change with time is called steady flow.
Example: Flow through a prismatic or non-prismatic conduct at a constant flow rate Q m3/s is steady.
Mathematically,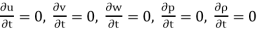 
Unsteady flow: It is that type of flow in which the velocity, pressure or density at a point change w.r.t. Time.
E.g.: the flow in a pipe whose value is being opened or closed gradually.
Mathematically,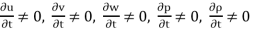 
Uniform and Non-uniform Flows
Uniform flow – The type of flow, in which the velocity at any given time does not change with respect to space is called uniform flow.
E.g.: Flow through a straight prismatic conduit.
Mathematically,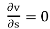
when t = constant
Non-uniform flow – It is that type of flow in which the velocity at any given time changes with respect to space.
E.g.: Flow through non-prismatic conduit.
Mathematically,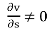
when t = constant
One, two & Three-dimensional flow
One dimensional flow – it is that type of flow in which the flow parameter such as velocity is a function of time and one space coordinate.
E.g.: Flow in a pipe where average flow parameters are considered for analysis.
Mathematically, u = f(x), v = 0 & w = 0
Two-dimensional Flow – The flow in which the velocity is a function of time and two rectangular space coordinates is called two-dimensional flow.
E.g.: Flow between parallel plates of infinite extent.
Mathematically, u = f1(x, y) v = f2(x, y) & w = 0
Three-dimensional flow – It is that type of flow in which the velocity is a function of time and three mutually perpendicular directions.
E.g.: Flow in a converging or diverging pipe or channel.
Mathematically, u = f1(x, y, z) v = f2(x, y, z) & w = f3(x, y, z)
Rotational and Irrotational Flows
Rotational Flow -A flow said to be rotational if the fluid particles while moving in the direction of flow rotate about their mass centers.
E.g.; Motion of liquid in a rotating tank.
Irrotational flow - A flow said to be rotational if the fluid particles while moving in the direction of flow do not rotate about their mass centers.
E.g.: Flow above a drain hole of a stationary tank or a water basin.
Laminar and Turbulent Flows
Laminar Flow – A Laminar flow is one in which paths taken by the individual particles do not cross one another and move along well-defined path.
E.g.: Flow of blood in veins and arteries.
Turbulent Flow – A turbulent flow is that flow in which fluid particles move in a zig zag way.
E.g.: High velocity flows in conduit of large size.
Compressible & Incompressible Flow
Compressible Flow – It is that type of Flow in Which the density () of the fluid changes from point to point.
E.g.: Flow of gases through orifices, nozzles, gas turbines, etc.
Mathematically, ρ≠ constant
Incompressible Flow – It is that type of flow in which density is constant for the fluid flow. Liquids are generally considered flowing incompressible.
E.g.: subsonic aerodynamics.
Mathematically, ρ= constant
Subcritical, Critical & Supercritical Flow
Subcritical flow– When Froude’s number is less than one the flow is known as subcritical flow.
Mathematically, Fr <1
Critical flow– When Froude’s number is equal to one the flow is known as subcritical flow.
Mathematically, Fr = 1
Supercritical flow– When Froude’s number is more than one the flow is known as subcritical flow.
Mathematically, Fr > 1
Key Takeaways:
- The type of flow in which the fluid characteristics like velocity, pressure, density, etc. at a point do not change with time is called steady flow.
- The type of flow, in which the velocity at any given time does not change with respect to space is called uniform flow.
- It is that type of flow in which the flow parameter such as velocity is a function of time and one space coordinate.
- It is that type of flow in which the velocity is a function of time and three mutually perpendicular directions.
The strain exerted via way of means of a static fluid relies upon handiest upon the intensity of the fluid, the density of the fluid, and the acceleration of gravity.
Pstatic fluid = ρgh
Where
ρ = m/V = fluid density
g = acceleration of gravity
h = depth of fluid
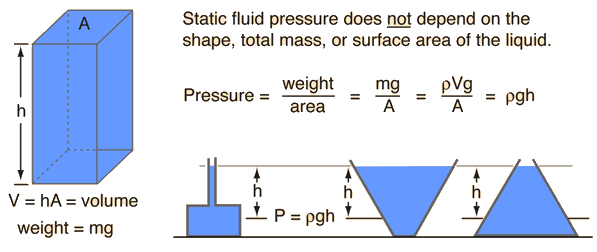
The maximum wonderful factor approximately this expression is what it does now no longer include. The fluid strain at a given intensity does now no longer rely upon the whole mass or overall extent of the liquid.
The above strain expression is simple to look for the straight, unobstructed column, however now no longer apparent for the instances of various geometry that are shown.
Because of the benefit of visualizing a column top of a regarded liquid, it has emerge as not unusual place exercise to nation all types of pressures in column top units, like mmHg or cm H2O, etc.
Pressures are frequently measured via way of means of manometers in phrases of a liquid column top.
Key Takeaways:
- The strain exerted via way of means of a static fluid relies upon handiest upon the intensity of the fluid, the density of the fluid, and the acceleration of gravity.
- The above strain expression is simple to look for the straight, unobstructed column, however now no longer apparent for the instances of various geometry that are shown.
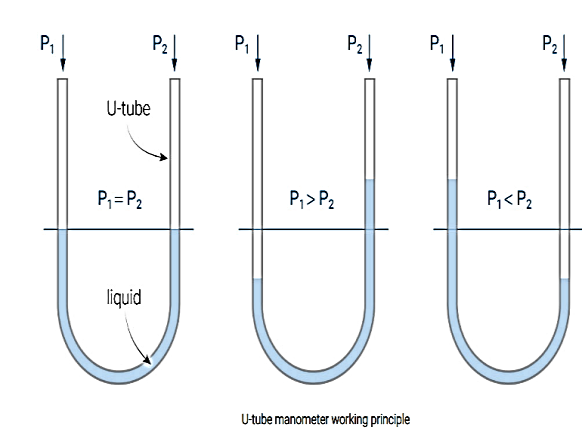
Principle of manometers
Hydrostatic equilibrium shows that the pressure when a liquid is at rest is equal at any point.
For example, if both ends of the U-tube are left open to the atmosphere then the pressure on each side will be equal. As a consequence the level of the liquid on the left-hand side will be the same as the level of the liquid on the right-hand side – equilibrium. However, if one end of the U-tube is left open to the atmosphere and the other connected to an additional gas/liquid supply this will create different pressures.
Balancing liquid column
Manometers measure a pressure difference by balancing the weight of a fluid column between the two pressures of interest. Large pressure differences are measured with heavy fluids, such as mercury (e.g. 760 mm Hg = 1 atmosphere).
Small pressure differences, such as those experienced in experimental wind tunnels or venturi flowmeters, are measured by lighter fluids such as water (27.7 inch H2O = 1 psi; 1 cm H2O = 98.1 Pa).
Pressure transducers
A pressure transducer is used to convert a certain value of pressure into its corresponding mechanical or electrical output. Measurement if pressure is of considerable importance in process industries.
The types of pressure sensors are differentiated according to the amount of differential pressure they are able to measure.
For low differential pressure measurement Liquid Column Manometers are used. Elastic type pressure gauges are also used for pressure measurement up to 700 MPa.
Types:
The manometer is defined as the devices used for measuring the pressure at a point in a fluid by balancing the column of fluid by the same or another column of liquid.
Simple manometers
A “simple manometer” is one which consists of a glass tube whose one end is connected to a point where pressure is to be measured and the other end remains open to atmosphere.
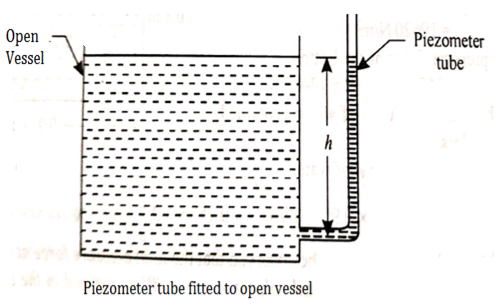
i) Piezometer:
- A piezometer is the simplest form of manometer which can be used for measuring moderate pressures of liquids.
- It consists of a glass tube inserted in the wall of a vessel or of a pipe, containing liquid whose pressure is to be measured.
- The tube extends vertically upward to such a height that liquid can freely rise in it without overflowing.
- The pressure at any point in the liquid is indicated by the height of the liquid in the tube above that point, which can be read on the scale attached to it.
- Thus if w is the specific weight of the liquid, then the pressure at point A(p) is given by p = wh
- A piezometer tube is not suitable or measuring negative pressure; as in such a case, the air will enter the pipe through the tube.
Ii) U-tube manometer:
- Piezometer cannot be employed when large pressures in the lighter liquids are to be measured since this would require very long tubes, which cannot be handled conveniently.
- Furthermore, gas pressures cannot be measured by a piezometer because gas forms no free atmospheric surface.
- These limitations can be overcome by the use of U-tube manometers.
- A U-tube manometer consists of a glass tube but in U-shape, one end of which is connected to a point at which pressure is to be measured and other end remains open to the atmosphere as shown in fig.
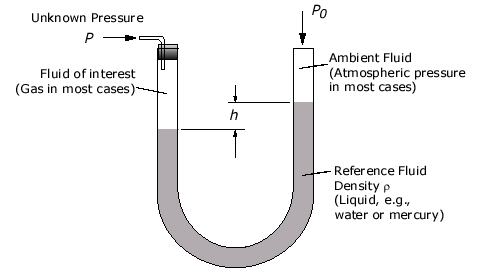
Gage Pressure ∆P = P – P0 = ρgh
Let A be the point at which pressure is to be measured. X-X is the datum line as shown in Fig(a)
Let, h1 = height of the light liquid in the left limb above the datum line
h2 = height of the heavy liquid in the right limb above the datum line
h = pressure in the pipe, expressed in terms of head
S1 = specific gravity of the light liquid, and
S2 = specific gravity of the heavy liquid
The pressure in the left limb and right limb above the datum line X-X are equal.
Pressure head above the X-X line in the left limb = h+h1S1
Pressure head above the X-X in the right limb = h2S2
Equating these two pressures, we get
h+h1S1= h2S2 or h = h2S2 – h1S1
For negative pressure:
Refer to fig(b)
Pressure head above x-x in the left limb= h+h1S1+h2S2
Pressure head above x-x in the right limb = 0
Equating these two pressures, we get
h+h1S1+ h2S2 = 0 or h =- h2S2 – h1S1
Iii) Inclined Single Column Manometer:
- This type of manometer is useful for the measurement of small pressures and is more sensitive than the vertical tube type.
- Due to inclination, the distance moved by the heavy liquid in the right limb is more.
l = length of the heavy liquid moved in right limb,
∝= inclination of right limb horizontal, and
h2 = vertical rise of liquid in right limb from x-x = l sin∝
h = l sin ∝ × S2 – h1S1
Differential Manometers
A differential manometer is used to measure the difference in pressures between two points in a pipe or two different pipes.
i) U-tube differential manometer:
A U-tube differential manometer is shown in fig.
Let, h = difference of mercury level (heavy liquid) in the U-tube,
h1 = distance of the center of A, from the mercury level in the left limb
h2 = distance of the center of B, from the mercury level in the right limb,
S1 = specific gravity of liquid in pipe A,
S2 = specific gravity of liquid in pipe B,
S = specific gravity of heavy liquid o mercury
hA = pressure head at A,
hB = pressure head at B
Considering the pressure heads above the datum line x-x, we get
Pressure head in the left limb:
hA+(h1+h)S1
Pressure head in the right limb:
hB+h2×S2+h×S
Equating the above pressure heads, we get
hA + (h1 + h)S1 = hB + h2 × S2 + h × S
(hA – hB ) = h2 ×S2 + h×S – (h1 +h)S1
Ii) Inverted U-tube differential manometer:
An inverted U-tube differential manometer is shown in fig.
It consists of an inverted U tube, containing light liquid, whose two ends are connected to the points whose difference pressures are to be measured.
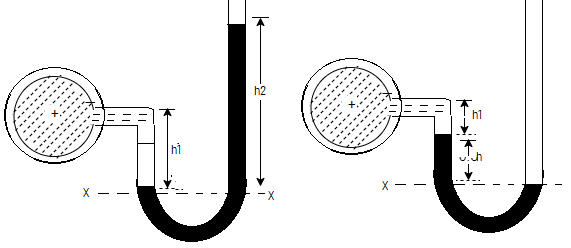
Let, h = difference of mercury level (light liquid) in the U-tube,
h1 = Height of liquid in the left limb below the datum line X-X
h2 = Height of liquid in the right limb below the datum line X-X
S1 = specific gravity of liquid in pipe A,
S2 = specific gravity of liquid in pipe B,
S = specific gravity of the light liquid
hA = pressure head at A,
hB = pressure head at B
Considering the pressure heads below the datum line x-x, we get
Pressure head in the left limb:
hA – (h1)S1
Pressure head in the right limb:
hB – h2 × S2 - h× S
Equating the above pressure heads, we get
hA - (h1)S1 = hB - h2 × S2 - h × S
(hA – hB ) = (h1)S1 – h2×S2 – h×S
Key Takeaways:
- Large pressure differences are measured with heavy fluids, such as mercury (e.g. 760 mm Hg = 1 atmosphere).
- The types of pressure sensors are differentiated according to the amount of differential pressure they are able to measure.
- A “simple manometer” is one which consists of a glass tube whose one end is connected to a point where pressure is to be measured and the other end remains open to atmosphere.
A Hydrostatics Law country that fee of growth of strain in a vertically downward path in fluid/liquid is identical to weight density of the liquid. To show that
Consider a three dimensional fluid element at rest along with the forces acting on it as shown in fig.
Weight of the element = w(dx∗dy∗dz)w(dx∗dy∗dz)
Px=pressure acting on the left face along x direction.
Px+(∂p/∂x)dx= pressure acting on the right face …..(as per Taylor expansion)
For equilibrium of the element;
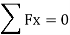
Px(dy × dz) = 
Divide above equation throughout by ‘dy × dz’ we get
Pz = Pz +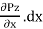 
∴ 
But dx ≠ 0
∴ 
Similarly for ‘z’ direction we can write,
∴ 
From (1) and (2) it can be concluded that there is no change in pressure in x and z direction at the same level or height. Hence ‘pressure at the same level in the fluid at rest remains constant’. Now for equilibrium in y-direction.
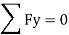
Py(dx × dz) = 
+ w. (dx × dy × dz)
Divide above equation throughtout by ‘dx × dz’ we get;
Therefore, Py = 
+w.dy =0
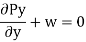
Substitute w = ρ.g in above equation we get ;
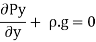
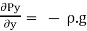………………………….(3)
Since Py = f(y) hence using perfect differentiation in relation (3)
Separating variables we get;
Dp = - ρ.g.dy
Integrating above equation we get;
p = - ρ.g.y +c …………………………………….(4)
Equation (4) is known as basic hydrostatic equation or hydrostatic law.
Pascal law states, "The intensity of pressure at a point in a fluid at rest is same in all direction. Consider an arbitrary fluid element of wedge shape in a fluid mass at rest as shown in Fig.
Let the width of the element be unity.
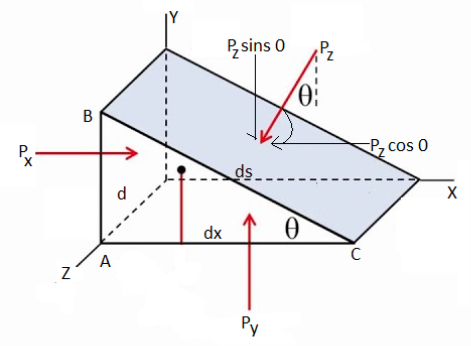
Let px, py, and pz, be the pressures acting on the face AB, AC and BC respectively.
Let ∠ABC=. Forces acting on the element are
Force on the face AB =Pressure in x-direction X Area of face AB
=px(dy × 1)
Force on the face AC = Pressure in y-direction x Area of face AC
=py(dx × 1)
Force on the face BC= Pressure in z-direction x Area of face BC
=pz(ds × 1)
Weight of the element = V × γ = A × 1 × γ = ½ × AC × AB × 1 × γ = dx.dy. γ/2
Consider the triangle ABC as shown in Fig.
Cos θ =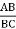 
sin θ =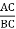 
BC cos θ = AB AC = BC sin θ
Ds cos θ = dx dx = ds sin θ
Resolve the force in x-direction we get
Px = Pz ….(1)
Resolve the forces in y-direction
Py = Pz …(2)
From Equations (i) and (ii),
Px = Py = Pz
- Since the choice of fluid element was completely arbitrary, which means the pressure at any point is same in all direction. Pascal's law states that, “The pressure or intensity of pressure at a point in a static fluid is same in all direction."
- It is used for the construction of machines such as hydraulic press, hydraulic riveter etc. in which by the application of relatively small forces considerably larger forces are developed.
Key Takeaways:
Pascal's law states that, "The pressure or intensity of pressure at a point in a static fluid is same in all direction."
- Have you ever seen a human tower? Consider the case of the man in the bottom line. You obviously carry a lot more weight than the guy in the first row. It is the same with the pressure of a liquid in a column. In the liquid column, as the depth increases, the pressure increases with it. And why is this pressure increasing? Because as it deepens, the liquid at lower depth should support the excess liquid as well. So to put it bluntly, we can say that
- Fluid pressure is the pressure within the fluid resulting from the weight of the liquid.
Liquid pressure can be calculated using the following relationships.
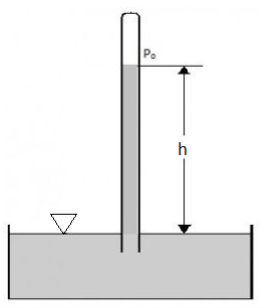
Fig: Fluid measurement
Pfluid = P + ρgh
Where,
P = Pressure on the reference area
P fluid is the pressure at a point in a fluid
ρ is the density of the fluid
g acceleration due to gravity (considering earth g = 9.8 m / s)
h height from the reference point
The volume of this liquid can be calculated by dividing the volume of the liquid by considering the volume of the extracted liquid.
ρ = m / v
Where,
m the size of the liquid
v is the amount of liquid considered
When the liquid is under atmospheric pressure there is a total systemic pressure provided by
Pfluid = Po + ρgh
Where,
Po atmospheric pressure
Conditions for Consideration of fluid pressure:
Water pressure is considered in two cases:
- In open condition or open channel flow
- In a closed case or in a closed ditch
The pressure of the liquid given above is static fluid pressure or hydrostatic pressure. The pressure here is considered to be based on the depth of the liquid only because the pressure generated as a result of the flow of the liquid can be considered minimal. The intensity of static fluid does not depend on the surface area, the composition of the liquid container or the total volume and volume of the liquid.
Remember that here, liquid refers to anything that has the ability to flow. Therefore, this refers to both beverages and gases.
Factors Affecting Fluid Pressure
There are two factors that affect liquid pressure. These two factors are the depth of the liquid and the quantity of it.
- Depth of fluid: As the depth increases, the pressure released by the fluid increases.
- Liquidity: A liquid as strong as water has a greater pressure than a liquid as light as air. The molecules in the denser fluid are close to each other leading to more collisions in a given area. This results in exertion and increased pressure.
Examples:
Q.1 Barometric reading at a place is 75 cm of Hg. Express the pressure intensity of 10 N per cm² is:
(1) m of water
(2) mm of mercury
(3) KN.m^2 abs
Soln.:
Given:
HHg = 75 mm = 0.75 m
Pgauge = 10 N/cm2 = 100 kN/m2
(i) In m of water,
P = γH
100 = 9.81 H
Hw = 10.19 m of water
(ii) In mm of mercury
P = γHhg
100 = 9.81 × 13.6 HHg
HHg = 749.5 mm
(iii) In kN/m absolute,
Patm = γHHg = (13.6 × 9.81) × 0.75
Patm = 11.06 kN/m2
Absolute pressure,
Pabs = Patm + Pgauge = 100.06 +100 = 100.06 kN/m2
Q.2 A gauge on suction side of pump shows a negative pressure of 0.285 bar. Express this pressure in terms of
1. Pressure intensity kPa
2. N/m absolute
3. m of water gauge
4. m of oil (S0.85) absolute
5. Cm of mercury gauge.
Take atmospheric pressure as 76cm of mercury and relative density of mercury as 13.6.
Soln:
1 bar = 10'^5 Pa
Gauge vacuum reading
Pvaccum = 0.285 ×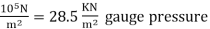 
Absolute pressure
Pabs = Patm + Pgauge
Patm = 76 cm Hg = hγS
Patm =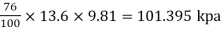 
Pabs = 101.396 – 28.5 = 72.896 kp
Equivalent head of water (gauge)
P=γh
h = p/γ = 28.5/9.81 = 2.905 m of water
Equivalent head of oil (absolute)
h = Pabs/ γ oil =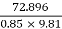 
= 8.742 m of oil (absolute)
Head of mercury (gauge)
h =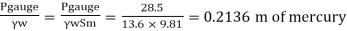 
h = 21.36 cm of mercury
Q.3 A cylinder contains a fluid at a gauge pressure of 350kPa. Express the pressure in terms of the column height of (a) water (o 1000kg/m) (b) Hg (S= 13.6). What would be absolute pressure in the cylinder if the atmospheric pressure is 101.3kPa?
Soln.:
Given:
Pgauge = 350 kpa, γ = ρg = 1000 × 9.81 = 9810 N/m3
(a) Pressure in term column head of water,
P = 𝛄h
h =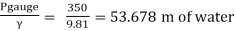 
(b) Pressure head in terms of Hg
h =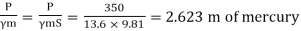 
(b) Absolute Pressure
Pabs = Pgauge + Patm = 350 + 101.3 = 451.3 kpa
Q.4 Mass density of a liquid varies as p = (1000+ 0.008 h). Where 'h' is depth (m) below free surface of liquid. Determine depth at which gauge pressure would be 100 kPa.
Soln.:
Given: ρ = 1000 + 0.008h, p = 100kpa
To find: Depth?
Pressure at any point
ρ = hγ = ρgh
100×103 = (1000 + 0.008h) 9.81h
h = 10.1932 m of water
Q.5 Measurements of pressure at the base and top of a mountain are 74cm and 60cm of mercury respectively. Workout the height of mountain if air has specific weight 11.97 N/m²
Soln.:
Pressure at top
SLγwh = 13.6 × 9.81 × 0.6 = 80.05 kN/m2
Pressure at bottom
SLγw. h = 98.728 kN/m2
P bottom – ptop = γh
h = 1.56 km
Key takeaways:
- Fluid pressure is the pressure within the fluid resulting from the weight of the liquid.
- The pressure of the liquid given above is static fluid pressure or hydrostatic pressure. The pressure here is considered to be based on the depth of the liquid only because the pressure generated as a result of the flow of the liquid can be considered minimal. The intensity of static fluid does not depend on the surface area, the composition of the liquid container or the total volume and volume of the liquid.
The total pressure is defined as the force exerted by a static fluid on a surface either plane or curved when the fluid comes in contact with the surfaces. This force always acts normal to the surface.
The centre of pressure is the point where the total sum of a pressure field acts on a body, causing a force to act through that point.
The middle of stress is the factor wherein the overall sum of a stress discipline acts on a frame, inflicting a pressure to behave via that factor. The overall pressure vector performing at the middle of stress is the fee of the incorporated sectorial stress discipline.
Pressure fields arise in each static and dynamic fluid mechanics. Specification of the middle of stress, the reference factor from which the middle of stress is referenced, and the related pressure vector permits the instant generated approximately any factor to be computed with the aid of using a translation from the reference factor to the favoured new factor.
It is not unusual place for the middle of stress to be positioned at the frame, however in fluid flows it's far viable for the stress discipline to exert a second at the frame of such value that the middle of stress is positioned out of doors the frame.
Key Takeaways:
- The centre of pressure is the point where the total sum of a pressure field acts on a body, causing a force to act through that point.
- The overall pressure vector performing at the middle of stress is the fee of the incorporated sectorial stress discipline.
Centre of Pressure
The Centre of pressure is defined as the point of application of the total pressure on the surface. There are four cases of submerged surfaces on which the total pressure force and center of pressure are to be determined. The submerged surfaces may be:
- Vertical plane surface
- Horizontal plane surface
- An inclined plane surface, and
- Curved surface
- Vertical plane surface
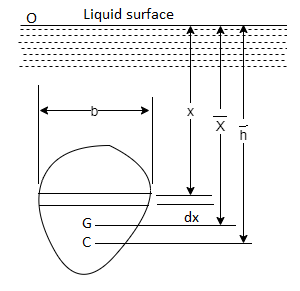
1. Vertical plane surface
Consider a thin horizontal strip of the surface of thickness dx and breadth b.
Let the depth of the strip be x.
Let the intensity of pressure on strip be p.
p =wx
Total pressure on the strip = p.bdx = wx.bdx
Total pressure on the whole area P =
=w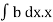 
But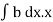
= Moment of the surface area about the liquid level =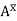 
P=w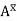
Moment of the pressure about free surface OO = (w.x.b. Dx).x = w.x2.b.dx
Total Moment, M =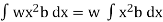 
But 
= Moment of inertia of the surface about free surface OO (I0)
Hence, M = wI0
The sum of the moment of the pressure is also equal to P×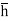 
.
P×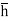
= wI0
w
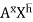= wI0
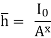
But I = IG + Ah2
Above eqn becomes
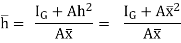
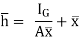
2. Horizontal plane surface
The total pressure on a horizontally immersed surface, as shown in Fig.above, is given by
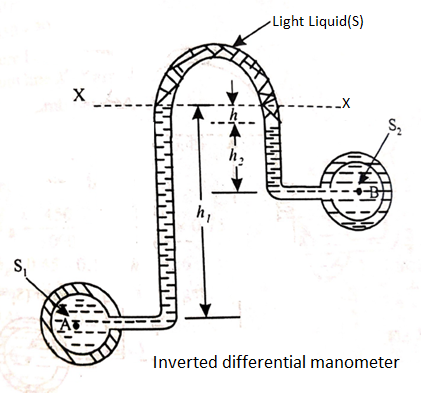
Where
w = Specific weight of the liquid,
A = Area of the immersed surface, and
x (bar) = Depth of the centre of gravity of the immersed surface from the liquid surface.
3. Inclined plane surface
Let A = area of the surface
= depth of the center of gravity from the free liquid surface.
θ=angle at which the immersed surface is inclined with the liquid surface.
w=specific weight of liquid.
Consider a strip of thickness dx width b at a distance l from O.
The intensity of pressure on the strip = wlsinθ
Area of strip = b.dx
Pressure on the strip =Intensity of pressure × area = wlsinθ × b.dx
The total pressure on the surface
P =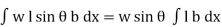
But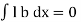 
ment of surface about OO =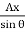
P= w sin θ.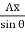 
= w. A
Let,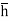 
= Depth of center of pressure below the free liquid surface
IG = Moment of inertia of the immersed surface about 00.
Moment of pressure about OO = wl sin θ b dx × l = w 
Sum of moments about O
M = 
But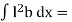 
I0 = Moment of inertia of the surface about point O
M = w sin θ 
Io
Sum of the moment of all such pressure about O is also equal to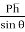 
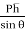= w sin θ Io
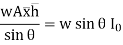
h =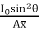 
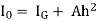
Where h = l =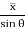 
= 
= 
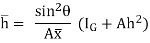
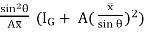
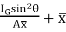
4. Curved surface
Consider a curved immersed surface LM submerged in a static fluid as shown in fig.
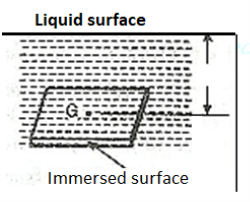
At any point on the curved surface, the pressure acts normal to the surface.
Thus, if dA is the area of a small element of the curved surface lying at a vertical depth of h from the surface of the liquid, then total pressure on the elemental area is
Dp = p × d A = wh × dA
This force dP acts normal to the surface. Further integration of the above eqn would provide the total pressure on the curved surface and hence
p=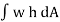 
But in the case of a curved surface, the direction of the total pressure on the elementary areas is not in the same direction but varies from point to point.
Thus, the integration of eqn. For the curved surface is impossible. The problem, however, can be solved by resolving the force P into horizontal and vertical components PH and PV. Then total force on the curved surface is
P = √(
Hence, the direction of the resultant force P
θ = tan-1 (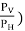
Where,
PH = Total pressure force on the projected area of the curved surface on the vertical plane.
PV = Weight of the liquid supported by the curved surface of the liquid.
Practical applications
- To calculate the total force acting on sluice gates of dams.
- To calculate the total force acting on the partial or fully immersed body.
- To calculate the reaction at the hinge.
- In designing lock gates in navigation chambers.
Key Takeaways:
- The Centre of pressure is defined as the point of application of the total pressure on the surface.
- Total pressure on the whole area P =
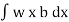
- Pressure on the strip =Intensity of pressure × area = wlsin θ × b.dx
- Archimedes’ principle, bodily regulation of buoyancy, found with the aid of using the historical Greek mathematician and inventor Archimedes, mentioning that any frame absolutely or partly submerged in a fluid (fuel line or liquid) at relaxation is acted upon with the aid of using an upward, or buoyant, pressure, the value of that is same to the load of the fluid displaced with the aid of using the frame.
- The extent of displaced fluid is equal to the extent of an item absolutely immersed in a fluid or to that fraction of the extent beneath the floor for an item partly submerged in a liquid. The weight of the displaced part of the fluid is equal to the value of the buoyant pressure.
- The buoyant pressure on a frame floating in a liquid or fuelling is likewise equal in value to the load of the floating item and is contrary in direction; the item neither rises nor sinks. For example, a deliver this is released sinks into the sea till the load of the water it displaces is simply same to its personal weight.
- As the deliver is loaded, it sinks deeper, displacing greater water, and so the value of the buoyant pressure constantly suits the load of the deliver and its cargo.
- If the burden of an item is much less than that of the displaced fluid, the item rises, as with inside the case of a block of timber this is launched under the floor of water or a helium-stuffed balloon this is set free in air. An item heavier than the quantity of the fluid it displaces, eleven though it sinks whilst launched, has an obvious weight reduction same to the burden of the fluid displaced.
- The buoyant pressure, which continually opposes gravity, is though due to gravity. Fluid strain will increase with intensity due to the (gravitational) weight of the fluid above. This growing strain applies a pressure on a submerged item that will increase with intensity. The end result is buoyancy.
Key Takeaways:
- The weight of the displaced part of the fluid is equal to the value of the buoyant pressure.
- For example, a deliver this is released sinks into the sea till the load of the water it displaces is simply same to its personal weight.
- An item heavier than the quantity of the fluid it displaces, eleven though it sinks whilst launched, has an obvious weight reduction same to the burden of the fluid displaced.
- Whenever a body is immersed wholly or partially in a fluid it is subjected to an upward force which tends to lift it up.
- The tendency for an immersed body to be lifted up in the fluid due to an upward force opposite to action of gravity is known as buoyancy.
- The force tending to lift up the body under such conditions is known as buoyant force or force of buoyancy.
- The magnitude of the buoyant force can be determined by Archimedes principle which states as follows:
- When a body is immersed in a fluid either wholly or partially it is buoyed or lifted up by a force which is equal to the weight of fluid displaced by the body.
Centre of Buoyancy
The point of application of the force of buoyancy on the body is known as the center of buoyancy. It is always the center of gravity of the volume of fluid displaced.
Equilibrium of floating and submerged bodies
Stability of floating Body:
The stability of a floating body is determined from the position of Meta-centre (M).
a). Stable Equilibrium
- If the point M is above G, the floating body will be in stable equilibrium as shown in Fig.
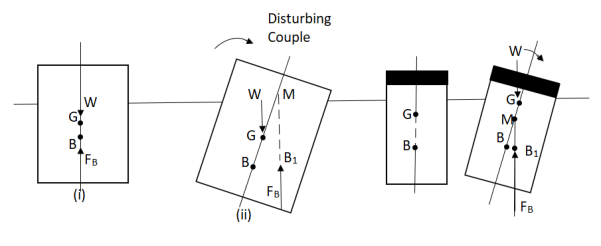
M is above G (stable equilibrium). M is below G (unstable equilibrium)
Fig: Stability of floating bodies
- If a slight angular displacement is given to the floating body in the clockwise direction, the center of buoyancy shifts from B to B1, such that the vertical line through B1 cuts at M.
- Then the buoyant force FB through B1 and weight W through G constitute a couple acting in the anti-clockwise direction and thus bringing the floating body in the original position.
b. Unstable Equilibrium:
- If the point M is below G, the floating body will be in unstable equilibrium as shown in fig.
- The disturbing couple is acting in the clockwise direction.
- The couple due to buoyant force FB and W is also acting in clock direction and thus overturning the floating body.
c. Neutral Equilibrium:
- If the point M is at the center of gravity of the body. The floating body will be in neutral equilibrium.
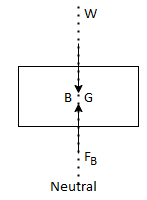
Stability of submerged Body:
- The position of center of gravity ¢er of buoyancy in case of a completely submerged body are fixed.
- Weight W acting vertically downward through G, while the buoyant force FB is acting vertical up through B.
Stable equilibrium:
When W = FB& point B is above G, the body is said to be in stable equilibrium.
Unstable Equilibrium:
If W = FB, but center of buoyancy B is below the center of gravity G, the body is in unstable equilibrium.
Neutral Equilibrium:
If W = FB & point B & G are at the same point, the body is said to be in neutral equilibrium.
Examples:
Q.1 A solid cube of sides 0.5 m each is made of material of relative density 0.5. Tho cube floats in a liquid of relative density 0.95 with two of its faces horizontal. Examine its stability.
Soln.:
Given:
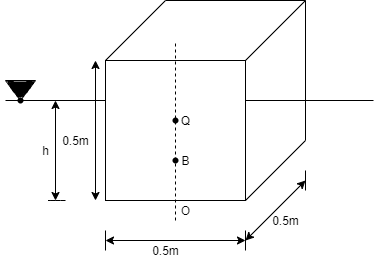
Side a=0.5 m
Relative density 0.5 m
Relative density of cube Sc= 0.5
Relative density of liquid S₁ = 0.95
Weight of cube = Weight of liquid displaced
Scγa3 = SLγ∀
0.5 × 0.53 = 0.95 ×∀
∀ = 0.06579 m3
Depth of immersion (h).
∀ = 0.06579 m3
Depth of immersion (h),
h = ∀/A = 0.263 m
Distance of C.G. From O.
OG = 0.5/2 = 0.25 m
Distance of buoyancy from O.
OB = h/2 = 0.1315 m
Now, BG= OG-OB=0.25-0.1315 = 0.1185 m
l/∀ = 0.0792 m
Metacentric height, BM-BG
l/∀ - BG = - 0.0393 m
Negative sign of metacentric height indicates that in unstable equilibrium.
Q.2 A rectangular pontoon is 5 m long, 3 m wide and 1.20 m high. The depth of immersion of the pontoon is 0.80 m in sea water. If the centre of gravity is 0.6 m above the bottom of the pontoon, determine the metacentric height. The density for sea water = 1025 kg/m².
Soln.:
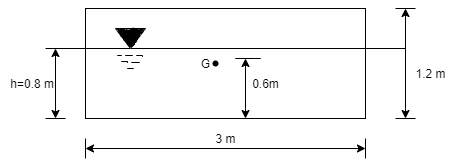
Volume of liquid displaced
∀ = LBh = 5 × 3 × 0.8 = 12m2
Moment of inertia
l = Lb3/12 = 5 × 33/12 = 11.25 m4
Metacentric height BM BG=
BM = l/∀ - BG = 11.25/12 – 0.2 = 0.7373 m
Key takeaways:
Whenever a body is immersed wholly or partially in a fluid it is subjected to an upward force which tends to lift it up.
The tendency for an immersed body to be lifted up in the fluid due to an upward force opposite to action of gravity is known as buoyancy.
The force tending to lift up the body under such conditions is known as buoyant force or force of buoyancy.
Stability of Submerged Body:
- Condition of stability for submerged body are based on relative positions of centre of gravity G and centre of buoyancy B.
Stable equilibrium
- When centre of buoyancy is lies above the centre of gravity, submerged body is stable. (Refer Fig.(a)).
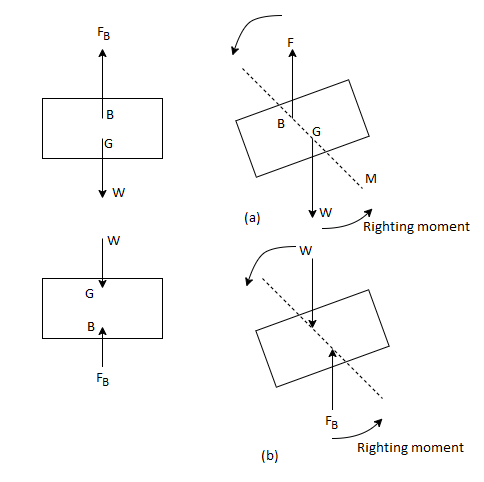
Unstable equilibrium
- When centre of buoyancy is lies below centre of gravity, submerged body is in unstable equilibrium. (Refer fig.)
Neutral equilibrium
- When centre of buoyancy and centre of gravity is coincided, body is in neutral equilibrium. (Refer Fig.)
Determination of Metacentric height:
- Let W1 is movable weight which is shifted by a distance x across the axis of tilt.
- Let
is the angle of tilt. - Moment due to shifted load, M₁ = W₁. x
- The moment M1 is balance by moment due to self-weight
M₂ = W x GG1
∵ tan θ = GG1/ GM
M2 = w× GM tan θ
∴ For stable equilibrium. M₁ = M₂,
W1x = w × GM tan θ
Metacentric height is, GM=w1x/w tan θ
Time of oscillation is obtained by
T = 2π 
Where k = radius of gyration
Numericals:
Q. On a certain planet a correctly calibrated spring balance shows the weight of a body s 12 N, the mass of which is 4.893 kg. Find the value of gravity on this planet.
Soln.:
Given:
Weight W= 12 N.
Mass m = 4.893 kg
Weight = Mass x acceleration
12 = 4.893 × g
g= 2.45 m/sec2
Acceleration due to gravity on a certain planet is 2.45 m/sec.
Q. The specific volume of a certain gas is 0.7m/kg Determine its specific weight and mass density.
Soln.:
Given:
Specific volume =0.7
To find: Mass density, specific weight
Mass density (p)
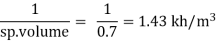
Specific weight (Y)
γ = ρg = 1.43 × 9.81 = 14.03 N/m3
Q. Liter of petrol weighs 14N. Calculate the specific weight, density, and specific gravity of petrol with respect to water.
Soln.:
Given: V=2 liter = 2 x 10-3m,
W=14N
To find:
- Specific weight,
- Density,
- Specific gravity.
Specific weight
γ = W/V = 14/ 2 × 10-3 = 7000 N/m3
Specific weight = Mass density x Acceleration due to gravity
7000 = ρ × 9.81
ρ = 7000/9.81 = 713.56 kg/m3
Specific gravity (S)
s = ρL/ρw = 0.7135
Q. A 400 ml of certain liquid weight 9N calculate the weight density and specific gravity of the liquid.
Soln.:
Given:
Volume V= 400 ml-0.4 L=0.4/1000=4x10^-4 m^3
Weight W=9N
To find: Weight density, specific gravity
1. Weight density (Y) =
γ1 = W/V = 
2. Specific gravity
s = ρL/ρw = 2.294
Q. What force is necessary to it a thin platinum wire ring of negligible thickness having 5 cm diameter from a water surface? Neglect weight of wire and consider surface tension of water as 0.0725 Nm.
Soln.:
Given: -
= 0.0725 N/m,
D= 5 cm = 0.05m
Force required to lift a than wire ring
F = πdσ = π× 0.05 × 0.072 = 0.0113 N
Q. Determine the minimum size of glass tube that can be used to measure water level, if the capillary rise in the tube is not to exceed 0.25 mm, Take surface tension of water in contact with air as 0.0735 N/m.
Soln.:
Given:
h=0.25 mm,
=0.0735 N/m,
To find: Minimum size of glass tube 'd'.
h =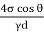 
For water θ = 0°, cos θ = 1
h = 
d =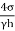 
d =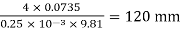 
Q. A rectangular plate 1.2 m x 0.4 m. Weighting 970N slides down a 45° inclined surface at a uniform velocity of 2.25 m/s. If the 2mm gap between the plate and the inclined surface is filled with oil, determine the viscosity of oil.
Soln.:
Given:
Area A = 12x04 0.48 m²
Weight of plate W =970 N
Velocity of plate u = 2.25 m/sec
Thickness of film t = dy = 2 mm = 2 x 10³ m
To find: Viscosity
Component of W along the plate= W sin θ
970 sin 45 = 685. 97 N
Shear force on the bottom surface of the plate
F= 685.89 N
τ = 
1428.94 = μ(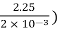
μ = 1.27 N -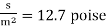 
The viscosity of the liquid is 12.7 poise.
Q. A pressure of 1.2 M Pascal is applied to 350 liters of liquid, causes a volume reduction of 1.5 liters. Calculate bulk modulus of elasticity for the liquid also find the compressibility.
Soln.:
Given:
Pressure p= 1.2M,
Pascal = 12x10 N/m².
Volume V 650 liter= 650 x 10³ m.
Reduction in volume dV= 1.5 liter= 1.5 x 10^-3 m3
Bulk modulus of elasticity, K
k =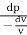 
k =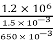 
k = 520 × 106 n/m2
Compressibility
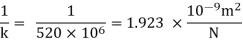
The Bulk modulus of elasticity for the liquid is 520 M Pa and compressibility is 1.923 x 10 m/N.
Key Takeaways:
- Moment due to shifted load, M₁ = W₁. x
- The moment M1 is balance by moment due to self-weight
References:
1. Introduction to Fluid Mechanics, James E.A., John and Haberm W.A., Prentice Hall of India
2. Fluid Mechanics, Jain A.K., Khanna Publication
3. Engineering Fluid Mechanics, Garde R.J. And MirajGoankar, Nemchand &Bros, Roorkee, SCITECH, Publication (India) Pvt. Ltd.
4. Fluid Mechanics and Fluid Power Engineering, Dr. D.S. Kumar, S.K. Kataria& sons
5. Fluid Mechanics, Frank M. White, McGraw Hill Publication
