Unit - 1
Concepts in machine element dynamics
Dynamics is the department of classical mechanics this is worried with the look at of forces and their consequences on movement.
Isaac Newton turned into the primary to formulate the essential bodily legal guidelines that govern dynamics in classical non-relativistic physics, specifically his 2nd regulation of movement. Generally speaking, researchers worried in dynamics look at how a bodily device may increase or regulate over the years and look at the reasons of these changes.
In addition, Newton hooked up the essential bodily legal guidelines which govern dynamics in physics. By analyzing his device of mechanics, dynamics may be understood. In particular, dynamics is usually associated with Newton's 2nd regulation of movement. However, all 3 legal guidelines of movement are taken into consideration due to the fact those are interrelated in any given statement or experiment.
Machine dynamics talk to the look at of a device’s movement based at the forces performing at the device. Machine dynamics practice expertise of engineering mechanics, specifically dynamics, to the troubles of actual machines. The effect of inertia and the incidence of vibrations play a primary function here. Machine dynamics make it feasible to expect the vibrational behavior of a device and, in which feasible, to compensate it.
Depending at the task, the vibrations can be desired (shakers, vibrating conveyors) or undesired (engines, turbines). Methods from vibration measuring era are used to check and examine vibrations.
Deflections of the device contributors are disregarded in standard with the aid of using treating device contributors as rigid bodies (additionally referred to as inflexible frame dynamics).
In different phrases the hyperlink should be properly designed to resist the forces without undue deformation to facilitate right functioning of the device. In order to layout the elements of a device or mechanism for strength, it's far vital to determine the forces and torques performing on character hyperlinks.
Each thing but small, have to be cautiously analysed for its function in transmitting force.
The evaluation is geared toward figuring out the forces transmitted from one factor to another, basically from enter factor to out positioned factor.
This will be the place to begin for energy layout of a element/ system, essentially to determine the scale of the components Force evaluation is crucial to keep away from both overestimation or below estimation of forces on gadget member.
Under estimation: results in layout of inadequate energy and to early failure. Overestimation: gadget element could have extra energy than required. Over layout results in heavier machines, more expensive and will become now no longer competitive Graphical evaluation of gadget forces could be used right here due to the simplification it gives to a problem, particularly in instances of complicated machines.
Moreover, the graphical evaluation of forces is a right away software of the equations of equilibrium. General Principle of pressure evaluation: A gadget / mechanism is a 3 dimensional object, with forces appearing in 3 dimensions. For a whole pressure evaluation, all of the forces are projected on to a few together perpendicular planes.
Then, for every reference aircraft, it's miles essential that, the vector sum of the implemented forces in 0 and that, the instant of the forces approximately any axis perpendicular to the reference aircraft or approximately any factor withinside the aircraft is 0 for equilibrium.
D'Alembert's precept, additionally called the Lagrange–d'Alembert precept, is a assertion of the essential classical legal guidelines of movement. It is known as after its discoverer, the French physicist and mathematician Jean le Rond d'Alembert. It is an extension of the precept of digital paintings from static to dynamical systems.
D'Alembert separates the whole forces performing on a device to forces of inertia (because of the movement of a non-inertial reference frame, now called fictitious forces) and inspired (all other) forces. Although d'Alembert's precept is formulated in lots of extraordinary ways, in essence it manner that any device of forces is in equilibrium if inspired forces are delivered to inertial forces.
The precept does now no longer practice for irreversible displacements, together with sliding friction, and greater fashionable specification of the irreversibility is required. D'Alembert's precept is greater fashionable than Hamilton's precept because it isn't always constrained to holonomic constraints that rely best on coordinates and time however now no longer on velocities
D’Alembert’s precept, opportunity shape of Newton’s 2nd regulation of movement, said through the 18th-century French polymath Jean le Rond d’Alembert. In effect, the precept reduces a hassle in dynamics to a hassle in statics.
The 2nd regulation states that the pressure F appearing on a frame is identical to the manufactured from the mass m and acceleration a of the frame, or F = ma; in d’Alembert’s shape, the pressure F plus the bad of the mass m instances acceleration a of the frame is identical to 0: F - ma = 0. In different words, the frame is in equilibrium below the motion of the actual pressure F and the fictional pressure -ma. The fictitious pressure is likewise known as an inertial pressure and a reversed powerful pressure.
Because unknown forces are extra without problems decided on our bodies in equilibrium than on transferring our bodies, the pressure and strain evaluation of device additives can typically be simplified through the usage of inertial forces.
When growing the formulation for the stresses in a rotating disk, for instance, it's far handy to expect that a consultant detail withinside the disk is in equilibrium below the motion of a device of radial and tangential forces produced through the stresses and an outward-appearing inertial (centrifugal) pressure. Equilibrium, in physics, the situation of a device while neither its kingdom of movement nor its inner power kingdom has a tendency to extrade with time.
A easy mechanical frame is stated to be in equilibrium if it stories neither linear acceleration nor angular acceleration; until it's far disturbed through an out of doors pressure, it'll preserve in that situation indefinitely.
A inflexible frame (through definition outstanding from a particle in having the assets of extension) is taken into consideration to be in equilibrium if, similarly to the states indexed for the particle above, the vector sum of all torques appearing at the frame equals 0 in order that its kingdom of rotational movement stays constant.
An equilibrium is stated to be solid if small, externally caused displacements from that kingdom produce forces that have a tendency to oppose the displacement and go back the frame or particle to the equilibrium kingdom.
Examples encompass a weight suspended through a spring or a brick mendacity on a stage surface. An equilibrium is volatile if the least departure produces forces that have a tendency to boom the displacement. An instance is a ball bearing balanced on the threshold of a razor blade.
D’Alembert’s principle can be explained mathematically in the following way:
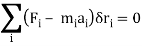
Where,
- i is the integral used for the identification of variable corresponding to the particular particle in the system
- Fi is the total applied force on the ith place
- mi is the mass of the ith particles
- ai is the acceleration of ith particles
- miai is the time derivative representation
- 𝜹ri is the virtual displacement of ith particle
Derivation of D’Alembert Principle
- Using D’Alembert’s mathematical formula, virtual work can be shown equal to D’Alembert’s principle, which is equal to zero.
- Following is the derivation:
Fi(T) = miai
(total force on each particle)
Fi(T) – miai = 0
(inertial force is moved left, representing quasi-static equilibrium)
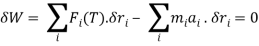
(equated to virtual work)
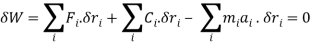
(separation of applied force and constraint force)

(final equation)
Up to now, all the structures that we've taken into consideration had been unmarried diploma of freedom structures for which one coordinate is enough to absolutely specify the configuration of the machine.
While there are various structures that may be fairly modeled as having a unmarried diploma of freedom, there are numerous different structures that require a extra unique model.
Discrete vibrating structures are categorised as both unmarried diploma of freedom (SDOF) and more than one diploma of freedom (MDOF) structures. There are many parallels among unmarried and more than one diploma of freedom structures. We will start our dialogue of MDOF structures with the aid of using thinking about diploma of freedom (TDOF) structures that are the simplest.
This will assist to demonstrate all the essential capabilities of MDOF structures whilst retaining the improvement as easy as possible. Once the 2 diploma of freedom machine is understood, extensions to structures with extra levels of freedom is straightforward.
Consider a machine constituted of hundreds and numerous springs as proven in Figure 8.1. This is a diploma of freedom machine given that coordinates are required to absolutely specify the configuration of the machine. One set of coordinates which may be used is x_1 and x_2, measured from the equilibrium position, as proven. However, this isn't the handiest set of coordinates which can be used. In fact, whilst x_1 and x_2 look like a herbal and logical choice, in a few experience there may be a higher choice, for motives to be mentioned shortly.
Preliminary Physical Reasoning
Before locating the real approach to this problem, don't forget precise preliminary displacements from the equilibrium configuration as proven in and spot what we will deduce approximately the ensuing movement.
In case (a), each hundreds are displaced an same quantity withinside the equal direction. In one of these displacement, the critical spring is neither stretched nor compressed (relative to its equilibrium length). Due to the symmetry withinside the machine, each hundreds will go through the equal movement in order that the space among them will continue to be constant.
The critical spring stays absolutely undeformed withinside the ensuing movement and applies no pressure at the hundreds. It consequently has no impact at the ensuing movement (i.e. for this precise preliminary displacement, the movement of the machine will be the equal if the critical spring had been now no longer gift as proven Having decided on the coordinates (x_1 and x_2) to explain the configuration of the machine, the subsequent step is to locate the equations of movement in phrases of the selected coordinates (and their Since that is a diploma of freedom machine, we can get equations of movement. There is normally one equation of movement in line with diploma of freedom withinside the machine.
There are many approaches to locate those equations, and maximum of those strategies are past the scope of this course. Here we can attention on using Newton’s Laws.
As with unmarried diploma of freedom structures, while drawing FBD/MAD’s we usually anticipate that each one of the coordinates and their derivatives are advantageous to get the perfect symptoms and symptoms withinside the equations of movement.
To make matters easier, you could additionally anticipate in case you want that one of the coordinates is greater than the different, say anticipate x_1 > x_2, even though it isn't essential to do so. Display the FBD/MAD for every of the hundreds withinside the machine.
The easy 1DOF structures analyzed withinside the previous phase are very useful to increase a experience for the overall traits of vibrating structures. They are too easy to approximate maximum actual structures, however. Real structures have greater than simply one diploma of freedom. Real structures also are very hardly ever linear.
You can be feeling cheated are the easy idealizations which you get to peer in intro publications definitely any use? It seems that they are, however you may best definitely be satisfied of this in case you realize how to investigate greater sensible problems, and spot that they frequently behave much like the easy idealizations.
The movement of structures with many tiers of freedom, or nonlinear structures, can not commonly be defined the use of easy formulation. Even after they can, the formulation are goodbye and complex which you want a laptop to assess them. For this reason, introductory publications usually keep away from those topics.
However, in case you are inclined to apply a laptop, reading the movement of those complicated structures is really pretty straightforward in fact, frequently less complicated than the use of the nasty formulation we derived for 1DOF structures.
Key Takeaways:
We will start our dialogue of MDOF structures with the aid of using thinking about diploma of freedom (TDOF) structures that are the simplest.
Precession is a extrade withinside the orientation of the rotational axis of a rotating frame. In the precise reference body it may be described as a extrade withinside the first Euler attitude, while the 1/3 Euler attitude defines the rotation itself.
In different words, if the axis of rotation of a frame is itself rotating approximately a 2d axis, that frame is stated to be precessing approximately the second one axis. A movement wherein the second one Euler attitude adjustments is known as nutation. In physics, there are sorts of precession: torque-unfastened and torque-induced. In astronomy, precession refers to any of numerous gradual adjustments in an astronomical frame's rotational or orbital parameters.
A crucial instance is the regular extrade withinside the orientation of the axis of rotation of the Earth, called the precession of the equinoxes.
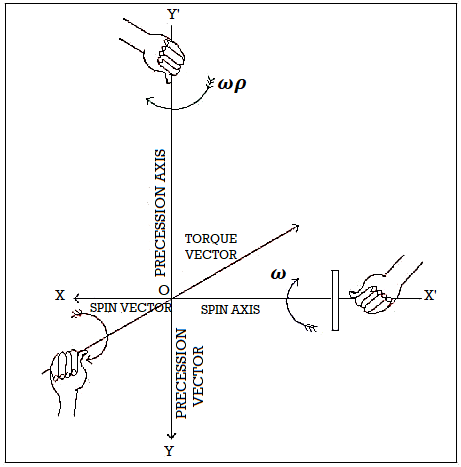
Precession, phenomenon related to the movement of a gyroscope or a spinning pinnacle and which include a relatively gradual rotation of the axis of rotation of a spinning frame approximately a line intersecting the spin axis.
The smooth, gradual circling of a spinning pinnacle is precession, the choppy wobbling is nutation. In the Figure the disk of weight W and the connected shaft are rotating at excessive velocity approximately the spin axis AB.
The angular velocity ω, that is clockwise considered from A, may be indicated both via way of means of the curved arrow ω withinside the aircraft of the disk or via way of means of the vector ω′ perpendicular to the disk and pointing to the proper.
The curved arrow ω and the vector ω′ are analogous, respectively, to the rotation and enhance of a proper-hand screw in a nut; that is called the proper-hand rule. It is typically greater handy to symbolize rotations and turning moments (which have a tendency to supply rotations) via way of means of vectors instead of via way of means of curved arrows.
The shaft and the desk bound column AC are linked via way of means of a ball-and-socket joint at A, which lets in the shaft to rotate approximately any line thru A. In the association proven withinside the Figure, the burden W creates a clockwise second WL approximately A, which may be represented via way of means of a vector M of importance WL, performing at A and perpendicular to AB.
Because of the instant, the shaft will process (rotate slowly) approximately the axis of the column in a clockwise direction, considered from C; the angular speed of precession is indicated via way of means of the vector Ω. It need to be stated that ω′, M, and Ω are at proper angles to each other and that the spin vector ω′ continually rotates towards the instant vector M.
It may be proven that Ω, the angular speed of precession, does now no longer rely on the perspective α, which, withinside the case of a spinning pinnacle, is near one hundred eighty degrees. The precession of tops is regularly observed via way of means of a phenomenon called nutation, that is evidenced via way of means of a wavelike movement of the give up of the spin axis as a result of versions withinside the perspective α.
In the Gyroscope a spinning wheel is used that's unfastened to transport and anticipate any axis. This takes place due to conservation of angular momentum. Due to angular momentum, the wheel continuously movements until any outside have an effect on is applied.
Gyroscope is used in lots of Places to hold and manual rotation. In the latest technological improvement there are different kinds of gyroscope has invented which matches on different principles. The electronic, fiber optical and so forth are the contemporary-day kinds of gyroscope which are being used.
When a wheel or disc is turned around or spin with a torque approximately an axis and with an angular velocity, a centrifugal pressure reacts at the system. This pressure create a reactive torque which has any other axis perpendicular to the axis wherein the disc is rotating.
Due to this the axis of rotation will precess or flip at an angle. The turning of the wheel relies upon on its path of rotation whether or not it's far clockwise or anticlockwise. If the wheel rotate approximately axis OX at anticlockwise path, the couple will act on the axis of couple.
Because of this couple the the wheel will pass alongside the aircraft of precession with an angle. The aircraft of precession may be perpendicular to the axis of precession.
Gyroscopic Couple Basic -‘Gyre’ is a Greek word, meaning ‘round movement’ and Gyration approach the whirling movement. A gyroscope is a spatial mechanism that's commonly hired for the look at of processional movement of a rotary body.
Gyroscope unearths programs in gyrocompass, utilized in aircraft, naval deliver, manipulate device of missiles and area shuttle. A gyroscope includes a rotor established withinside the internal gimbal.
The internal gimbal is established withinside the outer gimbal which itself is established on a set body as proven in Fig. When the rotor spins approximately X-axis with angular speed ω rad/s and the internal gimbal precesses (rotates) approximately Y-axis, the spatial mechanism is compelled to show approximately Z-axis aside from its personal axis of rotation, and the gyroscopic impact is consequently setup.
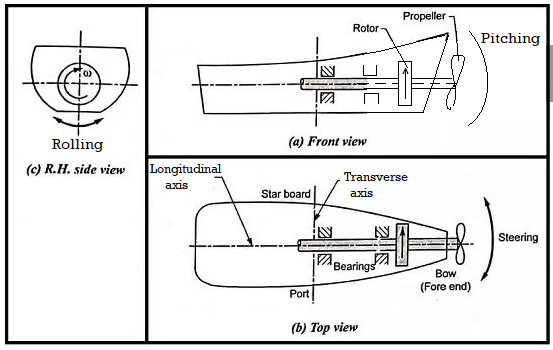
The resistance to this movement is known as gyroscopic impact. Gyroscope is used for stabilization and directional manipulate of a deliver crusing withinside the difficult sea. A deliver, even as navigating withinside the difficult sea, might also additionally enjoy the subsequent 3 specific kinds of movement:
(i) Steering—The turning of deliver in a curve even as shifting forward
(ii) Pitching—The motion of the deliver up and down from horizontal function in a vertical aircraft approximately transverse axis
(iii)Rolling—Sideway movement of the deliver approximately longitudinal axis. For stabilization of a deliver towards any of the above movement, the important requirement is that the gyroscope will be made to precess in this type of manner that response couple exerted via way of means of the rotor opposes the worrying couple which might also additionally act at the body.
Ship Terminology
(i) Bow – It is the fore quit of deliver
(ii) Stern – It is the rear quit of deliver
(iii) Starboard – It is the proper hand aspect of the deliver searching withinside the route of movement
(iv) Port – It is the left hand aspect of the deliver searching withinside the route of movement
Key Takeaways:
- Due to angular momentum, the wheel continuously movements until any outside have an effect on is applied.
- A gyroscope includes a rotor established withinside the internal gimbal.
The top and front view of an aeroplane are shown in Fig (a). Let engine or propeller rotates in the clockwise direction when seen from the rear or tail end and the aeroplane takes a turn to the left
Let ω= Angular velocity of the engine in rad/s,
m= Mass of the engine and the propeller in kg,
k= Its radius of gyration in metres,
I= Mass moment of inertia of the engine and the propeller in kg-m 2 = m.k2 ,
v= Linear velocity of the aeroplane in m/s,
R= Radius of curvature in metres, and
ωP= Angular velocity of precession
VR= rad/s
∴Gyroscopic couple acting on the aeroplane,
C=I.ω.ω
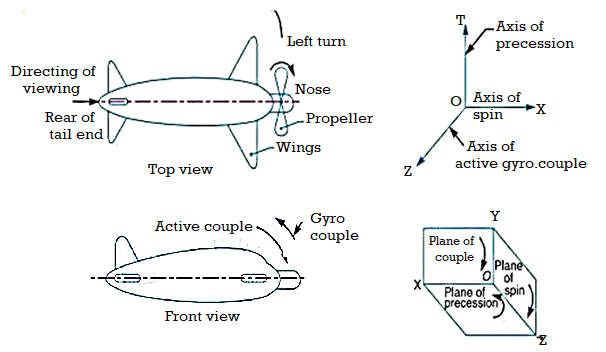
Before taking the left turn, the angular momentum vector is represented by ox. When it takes left turn, the active gyroscopic couple will change the direction of the angular momentum vector from ox to ox′ as shown in Fig.
The vector xx′, in the limit, represents the change of angular momentum or the active gyroscopic couple and is perpendicular to ox.
Thus the plane of active gyroscopic couple XOY will be perpendicular to xx′ , i.e.vertical in this case, as shown in Fig (b). By applying right hand screw rule to vector xx′, we find that the direction of active gyroscopic couple is clockwise as shown in the front view of Fig. (a).
In other words, for left hand turning, the active gyroscopic couple on the aeroplane in the axis OZ will be clockwise as shown in Fig. (b).
The reactive gyroscopic couple (equal in magnitude of active gyroscopic couple) will act in the opposite direction (i.e. in the anticlockwise direction) and the effect of this couple is, therefore, to raise the nose and dip the tail of the aeroplane
Ship:
The terms used are:
Bow: It is the fore or the front end of the supply.
Stern or aft: It is the rear end of the supply.
Types of Movements A sea supply can also have the following three actions:
Steering: It is the turning of a supply in a curve each to the right or to the left hand aspect at the same time as the supply actions forward.
Pitching: It is the upward or downward angular movement of the supply in a vertical plane, about its transverse axis, from the horizontal position.
Rolling: It is the sideway motion of the supply about its longitudinal axis. Now we can communicate the gyroscopic effect in a supply withinside the path of guidance, pitching, and rolling.
Steering isn't something but delivering a curve at the same time as the supply actions forward.
Due to this precession of the spin axis, the reactive gyroscopic couple is applied with the useful resource of the usage of the rotor shaft on the supply. It may be noted that effect of gyroscopic couple on a supply withinside the path of guidance may be very an entire lot much like that of an aeroplane taking turn to the left or right hand aspect.
Thus the gyroscopic effect on the supply withinside the path of guidance may be received withinside the similar way as for aeroplane. However, for better understanding, the same approach is repeated for the supply, as below.
Gyroscopic Effect During Steering while Rotor/Propeller Rotates in Clockwise Direction and Ship Steers Left while seen from the Stern Let the rotor/propeller rotates in clockwise course while seen from the stern and the supply steers left, as tested in Fig. Illustrates diagrammatically the course of reactive couple and its effect on the body of the supply, while rotor/propeller rotates in clockwise and aeroplane takes left turn, while seen from the stern.
Procedure to Determine the Direction of Gyroscopic Couple
Step 1: Locate course of spin vector Curl the fingers of the right hand along the course of rotation of rotor/propeller (in this case, along clockwise course), then the course of thumb indicates the spin vector.
Step 2: Obtain course of energetic gyroscopic couple vector Since the supply steers to the left, therefore with the useful resource of the usage of turning the spin vector via 90° withinside the course of precession, we get the course of energetic gyroscopic couple vector.
Step 3: Find course of reactive gyroscopic couple vector As we know, the course of reactive gyroscopic couple vector is opposite to the course of energetic gyroscopic couple vector, as tested in fig.
Step 4: Observe course of reactive gyroscopic couple Point the thumb of the right hand withinside the course of reactive gyroscopic couple vector, then the curling fingers supply the course of reactive gyroscopic couple.
Vehicles and grinding mills
Working assemblies of many machines and devices contain excessive-pace factors with a excessive second of inertia, rotating round a dynamic symmetry growing the so-known as gyroscope, their motion being known as the gyroscopic right motion.
When a gyroscope axis is motionless, system bearings are loaded with interplay: – operating one, because of an operation performed via way of means of a rotating element; – gravitational, because of interplay with gravitational area. Gyroscopic impact takes place in instances while the axis of quickly rotating hundreds could alternate its path.
Such a phenomenon takes place in operating machines of both chaff cutter kind or integrate harvester kind for the duration of turning or riding over abnormal surfaces. Subsequently, there's an additional, quick-converting load on bearings in slicing drums of a chaff cutter or rotating bearings of threshing assemblies in integrate harvesters, wherein there is an inclination of modifications withinside the path of a gyroscope axis.
This phenomenon additionally takes place in bearings of deliver propulsion turbine for the duration of converting of route while it movements together with the vessel across the vertical axis or in case of strong swaying because of waves.
In present day literature, there's no designated evaluation of the gyroscopic impact affects at the stability of forces load at the bearing factors. Subject place associated with kinematics and dynamics of system operating assemblies’ motion has already been mentioned in an in depth manner; however, modelling of the operating procedures has in no way taken the gyroscopic impact into attention.
Vital issue, with which the designers should cope, lies in suitable layout of machines geared up with quick rotating operating assemblies. It is feasible if all dependencies and family members because of the affects of the gyroscopic impact at the bearing load are completely identified and taken into account.
Due to universality of prevalence and availability of enter information for simulation calculations, the evaluation changed into performed for a operating system of a self-propelled chaff cutter kind. It changed into geared up with a excessive-pace drum slicing meeting placed withinside the system body.
Special attention have to be paid to this issue, as difficulty of slicing assemblies could be very topical, due to the fact they constitute the simple operating assemblies in a huge institution of agricultural machines for crop harvesting for lively purposes (biomass), fodder, as well as consumption.
The mathematical version advanced withinside the article takes completely into attention the instances of gyroscopic impact taking place because of the system turning and running over abnormal floor beneathneath area operational conditions.
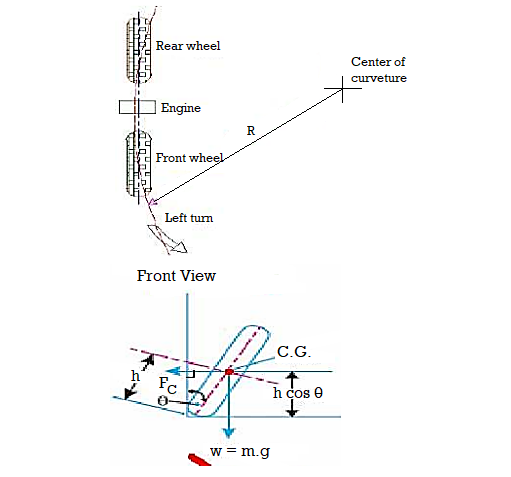
A vehicle running on the road is said to be stable when no wheel is supposed to leave the road surface. In other words, the resultant reactions by the road surface on wheels should act in upward direction. For a moving vehicle, one of the reaction is due to gyroscopic couple produced by the rotating wheels and rotating parts of the engine. Let us discuss stability of two and four wheeled vehicles when negotiating a curve/turn.
Fig shows a two wheeler vehicle taking left turn over a curved path. The vehicle is inclined to the vertical for equilibrium by an angle θ known as angle of heel.
Let m = Mass of the vehicle and its rider in kg,
W = Weight of the vehicle and its rider in newtons = m.g,
h = Height of the centre of gravity of the vehicle and rider,
RW = Radius of the wheels,
R = Radius of track or curvature,
IW = Mass moment of inertia of each wheel,
IE = Mass moment of inertia of the rotating parts of the engine,
ωW = Angular velocity of the wheels,
ωE = Angular velocity of the engine rotating parts,
G = Gear ratio = ωE / ωW,
v = Linear velocity of the vehicle = ωW rW,
= Angle of heel. It is inclination of the vehicle to the vertical for equilibrium
We know that,
V = ωW × rW
ωE = G .ωW or Angular momentum due to wheels = 2 Iw ωW
= 2 Iw v/r… ± IL G v/r…
= v/rw (2Iw ± GIE)
Angular momentum due to engine and transmission = IE ωE Total angular momentum (I xω) = 2 Iw ωW IE ωE Velocity of precession = ωp
Key Takeaways:
- The vector xx′, in the limit, represents the change of angular momentum or the active gyroscopic couple and is perpendicular to ox.
- Steering isn't something but delivering a curve at the same time as the supply actions forward.
References:
1. Theory of Mechanisms and Machines, Ghosh A. And Mallick A.K., Affiliated EastWest Press Pvt. Ltd., New Delhi, 1988.
2. Theory of Machines and Mechanisms, Shigley J.E. And Uicker J.J.,McGraw-Hill, Inc., 1995.
3. Mechanism and Machine Theory, Rao J.S. And Dukkipati R.V., Wiley-Eastern Limited, New Delhi, 1992.
4. Mechanics of Machines, John Hannah and Stephens R.C., Viva Books.
5. Theory of Machines, Sadhu Singh, Pearson Education.