Unit - 6
Equation of motion for two-degree-of-freedom system
There are equations for a diploma off d reed om device, one for every mass (exactly one for every diploma of freedom).
- If a harmonic answer is thought for every coordinate, the equations of movement cause a frequency equation that offers herbal frequencies of the device.
During loose vibration at one of the herbal frequencies, the amplitudes of the 2 levels of freedom (coordinates) are associated in a distinct way and the configuration is known as a ordinary mode, precept mode, or herbal mode of vibration.
- Thus a diploma of freedom device has ordinary modes of vibration similar to herbal frequencies.
- If we deliver an arbitrary preliminary excitation to the device, the ensuing loose vibration could be a superposition of the 2 ordinary modes of vibration.
As is obvious from the structures proven withinside the figures, the configuration of a device may be distinct with the aid of using a fixed of unbiased coordinates such as length, attitude or a few different bodily parameters.
Any such set of coordinates is known as generalized coordinates.
- Although the equations of movement of a diploma of freedom device are typically coupled in order that every equation includes all coordinates, it is constantly feasible to locate a selected set of coordinates such that every equation of movement consists of handiest one coordinate.
The equations of movement are then uncoupled and may be solved independently of every different. Such a fixed of coordinates, which ends up in an uncoupled device of equations, is known as precept coordinates.
The equations of movement for a diploma of freedom machine may be located the use of Newton’s 2nd law. Consider the machine proven in Figure 1 (b). The coordinates that absolutely describe the movement of this machine are x1(t) and x2(t), measured from the equilibrium role of every mass. External forces F1(t) and F2(t) act on loads m1 and m2 respectively. Using Newton’s 2nd law, we draw the loose frame diagrams of every mass as proven in Figure.
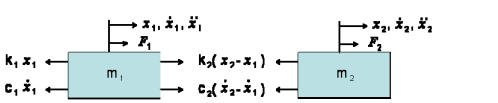
Figure: Free body diagrams for the masses in the two degree of freedom system
From these free body diagrams the equations of motion are easily found:
m1 .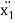 
+ (c1 + c2) . 
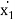- c2 . 
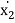+(k1+ k2) . x1 – k2 . x2 = F1
m2 .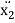 
- c2 . 
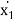- c1 . 
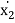- k2 . x1 – k2 . x2 = F2
Note that each equations incorporate each coordinates x1 and x2, as a consequence the differential equations are coupled. What this indicates bodily is that the movement of 1 mass impacts the movement of the other. It is beneficial to place the equations of movement into matrix form:
[m]{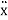
(t)} + [c]{ 
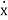(t)}+[k]{x(t)} = {F(t)}
[m] =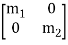
Where, [c] =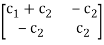 
[k] =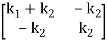 
{x} =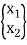 
And {F} =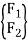 
The mass, damping, and stiffness matrices will continually be rectangular and of the size equal to the range of stages of freedom, (which in this example is 2). It is likewise vital to be aware that those matrices are generally symmetrical.
Natural frequency, additionally called eigenfrequency, is the frequency at which a gadget has a tendency to oscillate withinside the absence of any riding or damping pressure. The movement sample of a gadget oscillating at its herbal frequency is referred to as the everyday mode (if all elements of the gadget circulate sinusoidally with that identical frequency).
If the oscillating gadget is pushed via way of means of an outside pressure on the frequency at which the amplitude of its movement is greatest (near a herbal frequency of the gadget), this frequency is referred to as resonant frequency. Free vibrations of an elastic frame are referred to as herbal vibrations and arise at a frequency referred to as the herbal frequency.
Natural vibrations are distinct from compelled vibrations which manifest on the frequency of an carried out pressure (compelled frequency). If the compelled frequency is same to the herbal frequency, the vibrations' amplitude will increase manifold. This phenomenon is called resonance
The phrases “nature” and “herbal” are unified via way of means of one definition: “Existing in or initiated via way of means of nature; now no longer produced or suffering from humankind.”
This definition is simple and direct, however it additionally defines many phenomena that we, as humans, constantly take concept from to similarly each the sector of electronics and technological know-how as a whole. One such obviously taking place phenomenon is frequency, which encompasses diverse fields inclusive of the sector of electronics.
When speaking approximately digital gadgets and systems, we frequently are speaking in phrases of herbal frequency, which may be calculated with the herbal frequency formula. An item's herbal frequency is the frequency or price that it vibrates obviously while disturbed.
We name those sure function frequencies an item’s everyday mode. Moreover, herbal frequency includes diverse number one elements and they're as follows:
We name the frequency wherein an item obviously vibrates, its herbal frequency. We can make use of harmonic oscillators as equipment to version an item’s herbal frequency.
Natural frequencies are people who arise obviously while we disturb an item in a bodily manner, while gadgets that vibrate according with the software of a specific price are referred to as compelled frequencies. If we observe a compelled frequency this is equal to an item’s herbal frequency, the item will come upon resonance.
The Natural Frequency Formula Visualize a spring with a ball, which represents mass, connected to its end. While the ball and spring are stationary, the spring best in part stretches out, and our easy harmonic oscillator is in a function of equilibrium. Therefore, the anxiety from the springs is same to the gravitational pressure that draws the ball (mass) downward.
Once we circulate the ball far from its function of equilibrium, there are viable outcomes: It provides greater anxiety to the spring, i.e., it's far stretched downwards. It offers gravity the possibility to tug the ball downward without the anxiety from the counteracting spring, i.e., you push the ball upward. Regardless of which motion you take, the ball will start to oscillate approximately the equilibrium function.
This oscillating frequency is the herbal frequency, and we degree it in Hz (hertz). In summary, this can offer the oscillations in line with 2nd relying at the spring's residences and the ball's mass. Now, we can use the above instance to calculate the herbal frequency of a easy harmonic oscillator. When calculating the herbal frequency, we use the subsequent formula:
f = ω ÷ 2π
Here, the ω is the angular frequency of the oscillation that we measure in radians or seconds. We define the angular frequency using the following formula:
ω = √(k ÷ m)
This, in turn, adjusts our formula to the following:
f = √(k ÷ m) ÷ 2π
f is the natural frequency
k is the spring constant for the spring
m is the mass of the ball
Mode shapes
In easy language mode form is deformed pattern (mode) of item at that frequency. If u alternate the enter frequency then item will deformed at exceptional pattern (mode). Now u can also additionally ask, why it want to locate mode form.? Mode form companion with frequency. More truly we are able to recognize underneath example.
Example - If running frequency among 10 khz to fifteen khz for any device (method u working that device on such speed). And u have exceptional element contain in device say any link, shaft, cam, equipment or anything if any element have herbal frequency is in the range (10 - 15 khz), resonance will arise on that element & because of resonance big deformation appears. How deformation will seems like on resonance that may be are expecting with the aid of using checking mode form of additives in this frequency range.
Vibration absorber
Vibrations of rotor gadget are the supply of many faults in rotating equipment consisting of rotor-to-stator rub and shaft crack growth.
To hold the protection operation of the rotating equipment, the immoderate vibration of rotor gadget need to be controlled.
Many research was accomplished approximately vibration suppression techniques of rotor structures, which may be in large part divided into 3 kinds: vibration manage via way of means of making use of outside forces, vibration discount via way of means of adjusting parameters, and vibration soaking up via way of means of the use of dynamic vibration absorbers.
The first form of technique is via way of means of making use of outside forces that are typically produced via way of means of energetic magnetic bearings or energetic magnetic exciters.
The benefit of magnetic forces is they may be acted at the rotating elements contactless, consequently converting the shape of the rotor little. The strategies for controlling vibration are typically categorized as passive, energetic, semi-energetic or hybrid.
The evaluation of every of those strategies indicates important features. Each of those may be in comparison primarily based totally at the controlling efforts required and the overall performance of the strategies.
The use of inertia mass in vibration manage of mechanical systems is not unusualplace to the 3 specific controlling strategies. In structural engineering, taller and lighter homes are being built due to growing demands.
Due to the latest trends on top of things principle and programs of software program programs in engineering, controlling the dynamic behaviors of structural structures has been plenty easier.
The conventional techniques of reducing vibrations in systems have continually been via using passive design. They do now no longer require power and consequently they don’t generate undesirable states.
However, due to the fact they do now no longer have sensors, they don’t reply to adjustments that may be skilled with inside the vibrating systems or maybe the controlling device.
All of those motives have necessitated that extra studies be performed into using energetic vibration manage in mechanical systems.
Key Takeaways:
An item's herbal frequency is the frequency or price that it vibrates obviously while disturbed.
Therefore, the anxiety from the springs is same to the gravitational pressure that draws the ball (mass) downward.
Torsional oscillation of two-disc rotors:
If a shaft held in a bearing carries a rotor at each end, it will be vibrate torsion ally such that two rotors move in the opposite direction.
Therefor some length of the shaft is twisted in one direction while the rest is twisted in the other.
The section which is do not undergo any twist is called the nodal section
The shaft behaves as if clamped at the nodal section and the two sections vibrates as two separate shafts with equal frequencies.
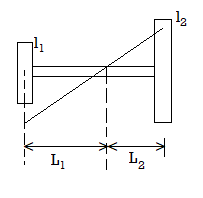
L1 and L2 = length of two portions of the shaft
L1 and l2 = MOI of rotor 1 and 2 respectively
q1 and q2 = torsional stiffness of lengths l1 and l2
f1 and f2 = natural frequencies of torsional vibrations of rotor 1 and 2 respectively
f1 = 1/2π q1/I1 and f2 = 1/2π q2/I2
At node point:
f1 = f2
q1/I1 = q2/I2
I1 < I2
According to the torsional formula:
T/J = T/r = Gθ/L
q = T/θ = GJ/L
At node point f1 = f2
q1/I1= q2/I2
GJ/L1I1 = GJ/L2I2
L1I1 = L2I2
I1/I2 = L2/L1
I1 < I2 L1 > L2
node point shifts towards the rotor of higher MOI.
Torsional oscillation of three disc rotors
We have selected a device and a fixed of parameters which might be optimized for each seeing and learning. Quite deliberately, we've selected a macroscopic and evidently seen mechanical device, which oscillates with intervals at the order of 1 2d so that scholars can see the conduct of the device on a human time scale. We have even supplied hands-on involvement. When making use of a torque via way of means of fingertip college students research pretty tangibly, the section courting required among the device's angular function and the implemented torque to be able to reap resonant excitation.
The Aluminum Rotor is clamped on the midpoint of the twine and different elements are connected to it. The Copper Disc each contributes to the instant of inertia and interacts with the magnetic brakes.
A scale on the brink of the copper disc permits visible dimension of angular deflection in radians Moveable magnetic brakes on both aspect offer variable eddy-modern magnetic damping Helmholtz coils have interaction with a dipole established at the rotor each to offer magnetic torques and to degree pace. Circuit Boards established below the device offer the non-touch capacitive angular-function transducer Motivated via way of means of the valuable function that the Simple Harmonic Motion performs in physics, and in physics education, TeachSpin has advanced an equipment that makes seen, tangible, on hand and MEASURABLE all of the capabilities essential to the physics of Simple Harmonic Motion.
Our new Torsion Oscillator turned into designed, from the floor up, to be a ultimate coaching device for the physics of the Simple Harmonic Oscillator at each degree.
An evaluation of the equipment: We've selected to make the most easy harmonic movement in angle. The aluminum 'rotor' shape is hooked up on the midpoint of a taut metallic twine.
A copper disc, focused at the twine, is established at the rotor. Torsional elasticity of the twine gives the 'spring regular' of the SHO. Rotational inertia of the rotor and copper disc offer the 'mass' of the SHO.
Helmholtz coils are connected to the cupboard in order that their axis passes each thru the metallic twine and thru the middle of a magnetic dipole device established at the rotor. Pulleys (now no longer shown) mount to the out of doors of the cupboard at the extent of the copper disc.
These capabilities permit college students to have direct get admission to to the immediate 'function' and 'pace' outputs of the device. They can view in actual time (on an oscilloscope withinside the XY-show mode, or on a computer) the country of the oscillator withinside the 'section plane' Because we picked a mechanical device that includes no frictional or sliding touch with the rotor, our SHO corresponds to a high-Q oscillator.
Damping via way of means of sliding friction yields a damping pressure it is impartial of the pace's magnitude; Paddles-on-hands may be effortlessly connected permitting research of fluid damping via way of means of air which offers a damping pressure about quadratic in pace.
Key Takeaways:
The Copper Disc each contributes to the instant of inertia and interacts with the magnetic brakes
Rotational inertia of the rotor and copper disc offer the 'mass' of the SHO.
Machine vibration is commonly analyzed with measurements of the vibration frequency, displacement, velocity, and acceleration. The latter three — displacement, velocity, and acceleration — are time area measurements, which means their amplitudes are plotted as opposed to time.
But those vibration indicators include beneficial information, inclusive of noise and harmonic content, which can be tough or not possible to discover while their amplitudes are plotted withinside the time area.
And due to the fact many vibration-associated troubles arise at particular frequencies, the motive and region of the vibration may be narrowed down or recognized primarily based totally on versions in amplitude at positive frequencies.
Every waveform may be expressed because the sum of easy sine waves with various amplitudes, phases, and frequencies. A Fourier remodel is a mathematical manner that converts a time area waveform into those man or woman sine wave additives withinside the frequency area — a manner regularly mentioned as “spectrum analysis” or “Fourier analysis.”
To recognize rapid Fourier transforms, it’s useful to first recognize the underlying manner, called discrete Fourier remodel (DFT). A discrete Fourier remodel exams the time area waveform for discrete, or man or woman, frequencies primarily based totally at the duration of the sign (N). The range of frequencies, or samples, required is same the sign duration squared (N2). Even for small indicators, this may take massive time and computing power. To make the Fourier remodel quicker and greater efficient, a technique called the quick Fourier remodel is used.
Any waveform is virtually simply the sum of a sequence of easy sinusoids of various frequencies, amplitudes, and phases. A Fourier collection is that collection of sine waves; and we use Fourier evaluation or spectrum evaluation to deconstruct a sign into its man or woman sine wave components.
The end result is acceleration/vibration amplitude as a feature of frequency, which shall we us carry out evaluation withinside the frequency domain (or spectrum) to advantage a deeper know-how of our vibration profile. Most vibration evaluation will normally be accomplished withinside the frequency domain.
Fourier evaluation works via way of means of “testing” for the presence of every frequency component.
A discrete Fourier rework (DFT) multiplies the uncooked waveform via way of means of sine waves of discrete frequencies to decide in the event that they fit and what their corresponding amplitude and section are. A speedy Fourier rework (FFT) is only a DFT the use of a greater green set of rules that takes gain of the symmetry in sine waves.
The FFT calls for a sign period of a few strength of for the rework and splits the manner into cascading corporations of two to make the most those symmetries. This dramatically improves processing speed; if N is the period of the sign, a DFT wishes N2 operations even as a FFT wishes N*log2(N) operations.
So for example, let’s take a sign period of 1024 (210); the DFT wishes 1,048,576 operations as compared to the lots greater green FFT and its 10,240 operations.
Although the execution time of an FFT can be quickest whilst the sign period is a few strength of two, modern computing strength and current FFT algorithms make this time distinction insignificant.
The wide variety of discrete frequencies which can be examined as a part of a Fourier rework is at once proportional to the wide variety of samples withinside the unique waveform.
With N being the period of the sign, the wide variety of frequency strains or packing containers is same to N/2.
These frequency packing containers arise at intervals (∆f) same to the pattern fee of the uncooked waveform (Fs) divided via way of means of the wide variety of samples (N), that's any other manner of pronouncing that the frequency decision is same to the inverse of the whole acquisition time (T).
To enhance the frequency decision, you need to amplify the recording time.
f = 1/T = Fs/N
The lowest frequency examined is zero Hz, the DC component; and the very best frequency is the Nyquist frequency (Fs/2). Windowing may be used to scale the frequency variety of hobby and manage the frequency bin width. There’s plenty that is going into expertise how windowing works and the way to pick out the proper feature in your application.
If this assessment at the math simplest whets your appetite, study this put up on Fourier Transforms. Enough math though! Let’s dive into a few examples to apprehend how spectrum evaluation may be used in your vibration checking out application.
Constructed Sine Wave and FFT Example
To illustrate how an FFT may be used, let’s construct a easy waveform with and use an FFT for vibration evaluation.
This built waveform will encompass 3 exclusive frequency components: 22 Hz, 60 Hz, and a hundred Hz. These frequencies can have an amplitude of 1g, 2g, and 1.5g respectively. The following determine suggests how this waveform seems a bit perplexing withinside the time area and additionally illustrates how the sign duration influences the frequency decision of the FFT.
The feature used to generate this waveform is to be had to download.
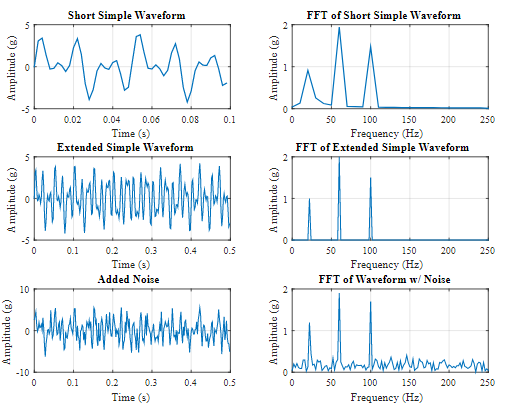
If we pattern this wave at a 500 Hz rate (500 samples in keeping with second) and take an FFT of the primary 50 samples we’re left with a quite jagged FFT because of our bin width being 10 Hz (Fs of 500 divided through N of 50). The amplitude of those frequency additives also are a chunk low. But if the variety is prolonged to the primary 250 samples as proven then the FFT is capable of as it should be calculate each the frequency and amplitude of the person sine wave additives.
This is the electricity of an FFT, it can surely perceive the primary frequencies that exist to assist the analyzer decide the reason of any vibration signal.
Key Takeaways:
- Fourier evaluation works via way of means of “testing” for the presence of every frequency component.
- If this assessment at the math simplest whets your appetite, study this put up on Fourier Transforms.
References:
1. Theory of Mechanisms and Machines, Ghosh A. And Mallick A.K., Affiliated EastWest Press Pvt. Ltd., New Delhi, 1988.
2. Theory of Machines and Mechanisms, Shigley J.E. And UickerJ.J.,McGraw-Hill, Inc., 1995.
3. Mechanism and Machine Theory, Rao J.S. And Dukkipati R.V., Wiley-Eastern Limited, New Delhi, 1992.
4. Mechanics of Machines, John Hannah and Stephens R.C., Viva Books.
5. Theory of Machines, Sadhu Singh, Pearson Education.
