Unit-6
Introduction To Vibration And Earthquake Analysis
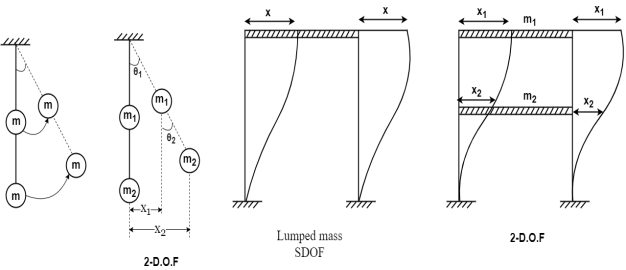
Definition:-The member of independent coordinates required to describe the position of A vibrating mass are termed as degree of freedom of that mass.
- When a mass is vibrating its position in space with repeat to its equilibrium position can be described by fixed to ordinates:-
Three translational along three orthogonal axes x ,y ,z .Three rotational about some axis.
Σfx=0, Σfy=0, Σfx=0
Σmx=0, Σmy=0, Σmz=0
2. However a mass may have freedom to move only in certain direction and may be constructed in other direction.
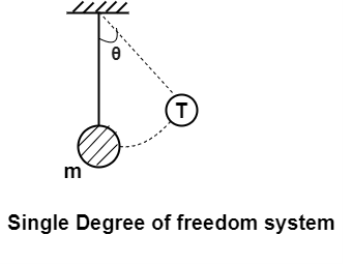
3. If a system is represented by single mass and it is constrained such that its motion is described by a single to ordinates it is termed as a single degree of freedom system.
4. For a multi mass discrete system the total degree of freedom would be some of degree of freedom of individual masses.
E.g.:-4-steryed building
Considering masses to be concentrated at floor level which are vibrates in one plane.
4-displacement for 4- masses would be described the deformed position of the structure it would be termed as 4-DOF.
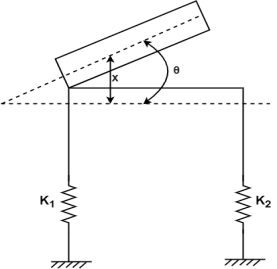
5. If one mass is attached to two springs and is free to vibrate in 2-independent deformed shape it would be termed as 2- degree of freedom of structures that ordinates will be required to describe the deformed position of the mass.
The independent two coordinates required to define the position of the mass are Q,K,X.
Definition:-
M model of a structure is an idealized representation of structure for purpose of analysis.
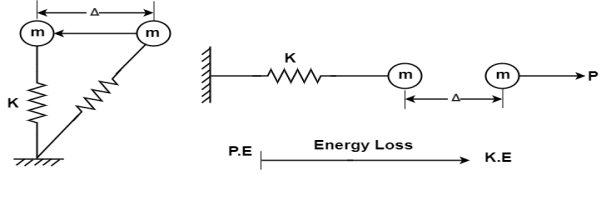
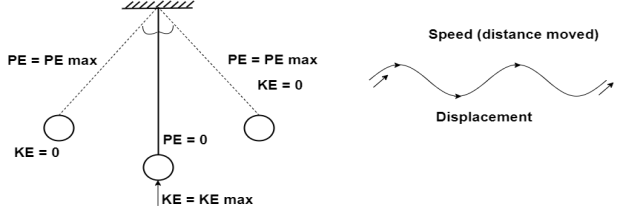
Let us consider a mass M fixed to the top of a column as shown in figure.1. A mass resting on roller of and fixed to a spring and a damping device.
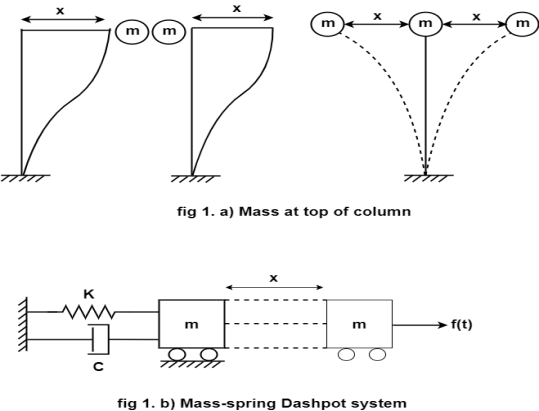
If the mass 'm' is 2 replaced by X the elastic straining of a column in.
a) the stretching of the spring
b) will tend to bring the mass back to the original position.
This sports extended by the column or spring is a function to the displacement X and it is termed as it restoring force or spring force structure of still K represents the combined stiffness of the column for later the formation and thus the inertial strain energy due to column deformation.
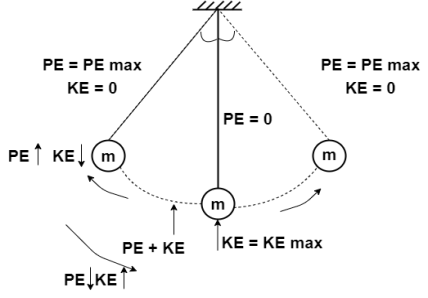
- Mass M is the total mass of the beam and slab of the frame as to storage for kinetic energy.
- This mass will come back to the original position with a certain velocity and will over to move other side and does vibrate forever
- But in practice friction with air friction between the particles of the system or at junction yielding of the materials etc. will despite this energy is that these vibrations will die out in course of energy of time.
- The forces which cause loss of energy are termed as dumping forces 'c' - damping coefficient.
Equation of motion for SDOF:-
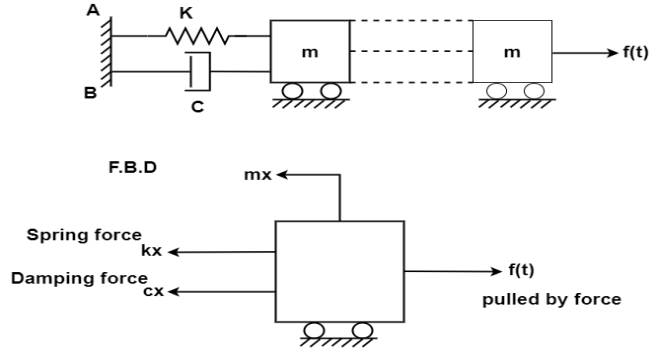
Let's consider a mass M attached to a fixed frame a b through a spring shown in figure 1 on an elastic system such as represented by forcewhich is a function of time and let the displacement be equal to X at any time t.
- The velocity and acceleration of the mass at some time would be x and x respectively taking positive in the positive direction of sx.
- Besides the exciting force FCT) the forces rating on the mass would be inertia force (Mx) spring force (kx) where,
K=storing force of that spring or elasticity of the portal frame which exerts for unit displacement and damping force (CX) where
C= coefficient of viscous damping in terms of force per unit velocity.
3. It should be seen that if the displacement X is towards right the spring force (kx) on the mass is edging towards left and is described by –ve sign.
4. Similarly damping force acts against the direction of velocity and would thus be acting towards left.
5. Considering FBD ab to mass the force is acting on it r are.
F(F) =kx - cx
By newton's second law of motion these forces are equal to mx
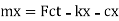
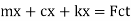
Distance= velocity* time
Velocity/speed=
Retardation =-ve sign indicate opposite direction of displacement
Forces designated as frictional damping force are always present in any physical system undergoing these forces dissipate energy more precisely the under presence of these frictional forces constitutes through which the mechanical energy of the system kinetic and potential energy of the system is transferred to other forms of energy such as heat.
The stamping of friction forces proportional to the magnitude of velocity and off to the direction of motion this type of damping is known as viscous damping.
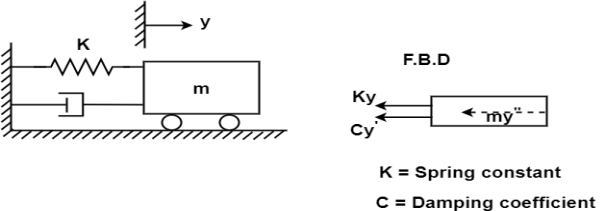
K= spring constant
C= damping coefficient
Using D'Alembert’s principle we can write equation of equilibrium to obtain equation of motion.
Summation of forces in y direction
-----------1
Solution of differential equation 1 is
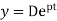
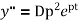
Substitute 2 in 1 we get
----------------3
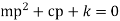
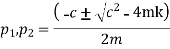
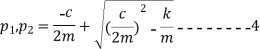
Thus the general solution of equation 1 is given superposition of the two possible solutions namely.
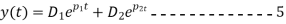
Where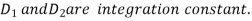 
The final solution form of equation V depends on the sign the expression under the radical in equation 4.
Three distant cases may occur.
- Quantity under the radical may be zero=critical damping
- The quantity under the radical male positive=overdamped.
- The quantity under the radical may negative=underdamped
Critical damping:-difference between nature and damping frequency is zero.
Overdamped:-difference in positive
Underdamped:-difference in negative
Case 1:- Critically damped system
The limiting case in which the quantity under radical is zero the damping present in this case is called critical damping.
This means that the expression under root of equation 4 in equal to zero
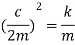
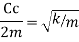
Cc= 2mw
In critically damped system the roots of characteristic equation are equal and from equation 4.
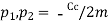
Since the roots are equal the general solution given by equation 5 would provide only one independent constant integration, hence
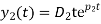
The general solution for the critically damped system is then given by the superposition of these two solutions
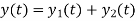
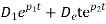
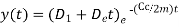
We know that,
=
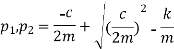
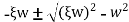
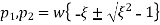
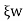
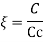
Case 2:- over damped system
In and overdamped system the damping coefficient is greater than the value of critical damping i.e. C>Cc also
Expression in the radical of equation 4 thus the solution is
‘
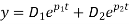
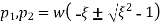
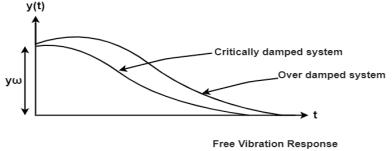
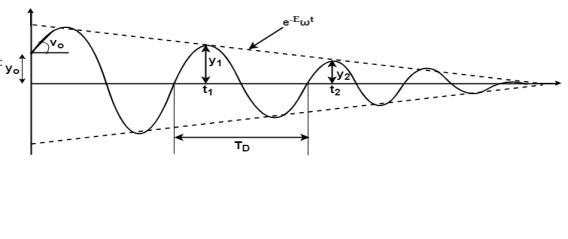
Case 3:- under damped system
In case of underdamped system damping coefficient is less than critical value C<Cc, which occurs when the expression on the radical of equation 4 is negative.
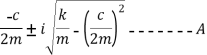
Where i=
imaginary unit
For this case, we use Euler’s equation which relates exponential and trigonometric functions. Namely,
Substitute A in equation 5 ,we get
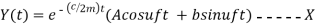
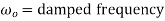
---------C
Finally when the initial conditions for displacement find velocity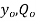
Are introduced the constant of integration can evaluated and substituted in equation X we get,
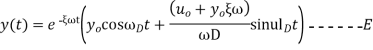
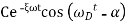
Where
C= max. Amplitude
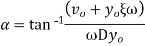
Earthquake is the result of vibration of earth surface by seimic waves coming from source of disturbance which is situated inside the earth most of the earthquakes are caused by ship along geological faults.
The waves generated by an earthquake are of three types
- Primary (p) waves
- Secondary (s) waves
- Surface waves.
Primary waves are also known as push-pull waves are longitudinal waves compressional waves these waves propagate by longitudinal or compressive action grounds get alternately compressed and dilated in the direction of propagation.
Secondary waves are also called transverse waves. In comparison to P- waves, s -waves are slow. Because of the waves, ground gets displays perpendicularly to the direction of propagation.
When the vibrator waves energy is propagating near the surface of the earth, two other types of wave known as Rayleigh and fav can be identified these are known as surface waves as they are confined to the surface layers of the earth only.
Use of systemic coefficient method As given inIS:-1893 can be carried out to compute forces and moments in the member.
This method design base is calculated from
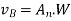
Where,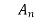
= Design horizontal acceleration spectrum
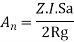
Where Z=zonal factor given in IS:-1893 ,
Table 2:-
Value Z
Zone | Value of z |
2 | o.10 |
3 | 0.16 |
4 | 0.24 |
5 | 0.36 |
I= important factor depending on the functional use of structure (table 6 of IS:-1893) I=1 and 1.50
R=Response reduction factor depending on Pereceivedsiesmic damage performance of structure (Table-7, IS:-1893).
R= 3 to 5 for movement resistant RC structures.
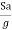= Average response acceleration coefficient is given bye figure 2 and table 3 of IS:-1893.
W= seismic waves of the building
The seismic weight of the whole building is the sum of the systemic weights of all the floors and will include 25% and 50% of L. For floors in case of LL limit upto 3 kN/m and above 3 kN/m and L.L on roof is to be considered.
Sa/g values are obtained on the basic of fundamental/ natural/period of vibration.
For moment resistant buildings with brick fell,
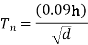
Where,h= height of building excluding basement story
d=best dimensions of building at plinth level along the considered direction of lateral forces.
For moment resistant building without brick fills.
Period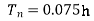
for R.C framed building
Values of Sa/g based on 5% damping
Types of soil | Sa/g values |
Rocky or hard soil | 1+IST for 0.00 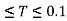 2.50 for 0.10  100/T for 0.40  |
Medium soil sites | 1715 T for 0.00  2,50 for 0.10 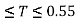 1.36/T for 0.55  |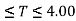
Soft soil sites | 1715T for 0.00<=T<=0.10 2.50 for 0.10<=T <=0.60 1.67/7 for 0.60 <=T<=4.00 |
Multiplication factors | 3.20 | 1.40 | 1.00 | 0.50 | 0.80 | 0.70 | 0.60 | 0.55 | 0.50 |
Damping % | 0 | 2 | 5 | 7 | 10 | 15 | 20 | 25 | 30 |
Design base sheer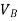 
shall be distributed as nodal loads on different floors
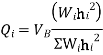
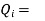Design lateral bed on floor
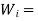Seismetic wt of floor
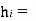height of floor I measured from base
Problems Based On Seismic Coefficient Method.
6.5.1 a four storey building has the following data
Overall plant dimensions=20m×16m
Number of boys 4m each in X direction=5
Number of boys 4m each in y direction=4
First storey height=4m
Height of 2nd,3rd ,4thstorey=3m
Size of beams=300mm×600mm
Size of columns=150mm
Live load=3.5Kn/m on floors and 2Kn/m on roof
External missionary walls of the thickness 230 mm and internal walls of 115 mm thickness have been provided.
Building located in Pune on hard strata with 5% damping evaluate the specific weight of each floor and hence total seismic weight of building calculate the base shear using seismic coefficient method.
Answer:
- Pune location, zone-3 ,Z=0.16( Table 2, IS:-1893)
From table 6 important factor I=1(all other buildings).
Assume the building as special moment resisting frame.
Response reduction factor R=5(Table 7, IS:-1893)
2. Seismic weight:-
Floor area=20×16=320m
Assume DL=10Kn/m
Total seismic weight on floors
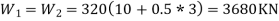
Roof:-
Total seismic weight of the structure W=ΣWi=3*3680+3200
14240KN
3. Fundamental period:-
Lateral load resistance is provided by moment resisting frames infilled with brick marnry panels
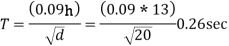
From figure 2 of IS: 1893 part I , for T =0.26 sec
Sa/g=2.5
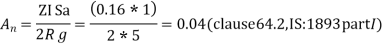
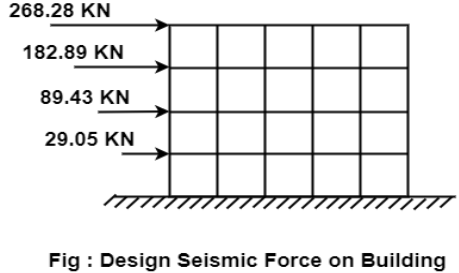
4. Design base shear:-
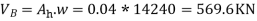
The design base shear is to be distributed with height as per class 7.71 , IS: 1893m part I
Storey hard | Wi | Hi (m) |  |  |  |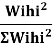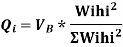
4 | 3200 | 18 | 540.8 | 0.471 | 268.28 |
3 | 3680 | 10 | 368 | 0.321 | 182.84 |
2 | 3680 | 7 | 180.32 | 0.157 | 89.43 |
1 | 3680 | 4 | 58.88 | 0.051 | 29.05 |
 |
|
| 1148 | 1000 | 569.60 |
6.5.2 For a symmetrical small telephone exchange office building of size 8m×8m having 2 equal bays has a height of 10.5 m with each storey having weight 3.5 M the building is located in zone V soil. Conditions is medium stiff SMRF is adopted. DL=10KN/m and IL=3KN/m .determine the design seismic forces for the building using seismic coefficient method as per IS:-1893 and show the distribution of Rachel forces with the building height.
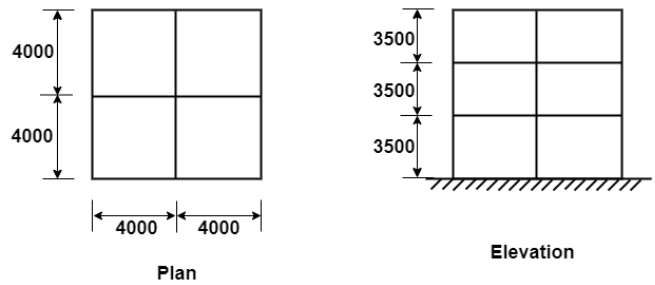
Answer:
- Design parameters:-
For seismic zone v, zone factor Z=0.36(Table 2,IS:-1893).
Being an office building, important factor I=I(Table 6,IS:-1893).
For SMRF building response reduction factor R=5(Table 7,IS:-1893)
2. Seismic weights:-
Floor area=8×8=64m
Hive load class is 3KN/m hands as per table 8 IS:-1893 25% of live load is lumped at the floor at roof no live load is to be tempt hence total systemic weight on the floor and roof is
Floors:-
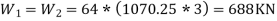
Roof:-
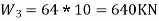
Total seismic weight of the structure W =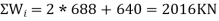 
3. Fundamental period:-
Lateral load resistance is provided by moment resisting frames in filled with break missionary panels.
EL in x-direction & y- direction
The building is located on type-2 (medium soil)
From figure 2 of IS 1893 , for T=0.33 sec
Sa/g= 2.5
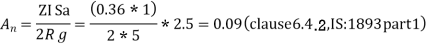
4. Design base shear :-
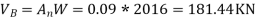
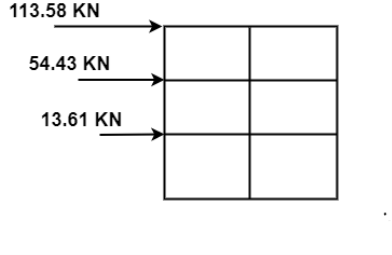
The design base shear is to be distributed with height as per clause 7.7.1 , IS:-1893 part -1
Story hand | Wi | Hi |  |  |  |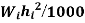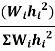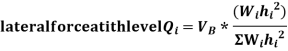
3 | 640 | 10.5 | 70.65 | 0.626 | 1 |
2 | 688 | 7 | 33.71 | 0.300 | 54.43 |
1 | 688 | 3.5 | 8.43 | 0.075 | 13.61 |
 |
|
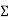| 112.79 | 1.000 | 181.44 |
6.5.3 calculate the base shear for unbraced building located in Pune the building is having plant dimensions 25m×25m having five similarly bays in both direction. The soil conditions are medium stiff. The R.C frames are in field with break imaginary the lumped weight due to dead loads is 12KN/m flowers and 10 KN/m on the floor and 1.5KN/m on the roof. The total height of the building is 1km with floor height as 3.5 M also show sure distribution over the height of the building.
Answer:
- Design parameter:-
Pune located ,zone 4, Z=0.16 (Table 2,IS 1.89 3 part 1).
Importance factor I=1(table 6,IS 1893 part 1)
OMRF building response reduction factor R=3(Table 7,IS:-1893).
2. Seismic weights:-
Floor area=25×25=625
Hive load class is for KN/m, hence as per table 8, IS 1893 part 1, 50% of the live load is lumped at the floors. At roof no live load is to be lumped.
Hence, total system equates on the floor and roof is:-
Floor:-
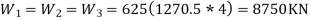
Roof:-
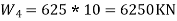
Total seismic weight of the structure W= ΣWi=3*8750+6250 = 32500KN
3. Fundamental time period:-
Lateral load resistance is provided by moment resisting frames in field with brick masonry panels.
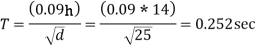
The building is located on type 2 (medium stiff soil)
From figure 2 of IS ; 1893 , for T =0.252 sec
Sa/g= 2.5
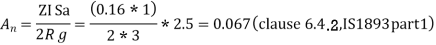
4. Design base shear:-
The design base share is to be distributed with height as per clause 7.7.1, IS:-1893 part 1
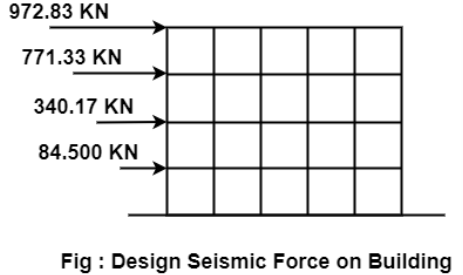
Story level | Wi | Hi |  |  |  |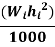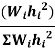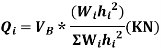
4 | 6250 | 14 | 1225 | 0.449 | 972.83 |
3 | 8750 | 10.5 | 964.69 | 0.356 | 771.33 |
2 | 8750 | 7 | 428.75 | 0.157 | 340.17 |
1 | 8750 | 3.5 | 107.19 | 0.039 | 84.500 |
 |
|
| 2725.63 | 1.000 | 2166.67 |
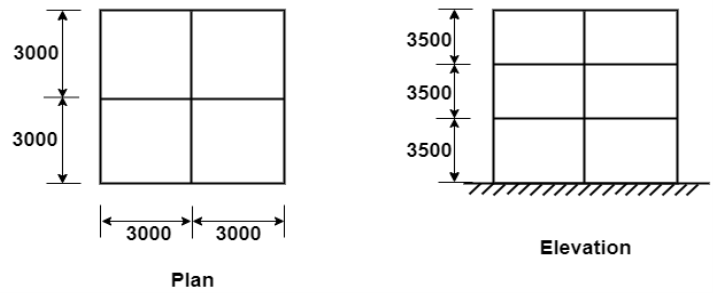
6.5.4 A residential building of size 6 m×6 m having two equal bays has a height of 10.5 m with each story heaven heights 3.5 M the building is located in zone3 soil condition is medium stiff.OMRF is adopted DL=10KN/m and IL=2 KN/m. Determine the designs seismic forces for the building using sizzling coefficient method as per IS=1893 and show distribution of little forces with the building height
Answer:
- Design parameters:-
Zone 3 building ,z=0.16 ( Table 2,IS:-1893part 1).
Importance factor:-I =1( Table 6, IS:-1893 part 1).
For OMRF building, response reduction factor R=3(Table 7,IS:-1893 part 1).
2. Seismic weight:-
Flower area=6×6=36m
Assume live bad class as 3kN/mhence as per table 8 IS:-1893. Part 1 25% of life that is to be lumped at floors are prove no live load is to be lumped. Hence, total systemic weight on the floor and roof is
Floors:-
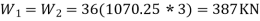
Roof:-
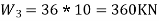
Total seismic weight of the structure 
3. Fundamental time period:-
Lateral load resistance is provided by moment resisting frames in field with brick masonry panels.
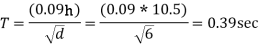
The building is located on type two medium stiff soil.
From fig 2 of IS; 1893 part 1 , for T= 0.39 sec
Sa/g=2.5
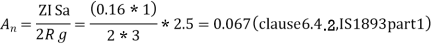
4. Design base shear:-
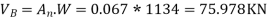
The design based share is to be distributed with height as per clause 7.71,IS:-1893 part 1.
Story level | Wi | Hi |  |  |  |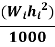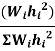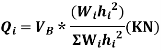
3 | 360 | 10.5 | 39.69 | 0.626 | 47.56 |
2 | 387 | 7 | 18.963 | 0.299 | 22.72 |
1 | 387 | 3.5 | 4.74 | 0.075 | 5.70 |
 |
|
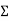| 63.393 | 1.000 | 75.978 |
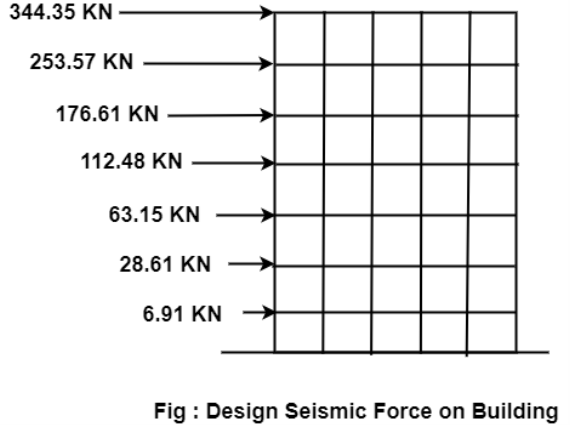
6.5.5 For an unbraced building having plan dimensions 30m×30m, to the total service McLeod on a frame having five similar base is 14800 KN. The building is situated in zone 3. Footing is resting on medium soil. The total height of the building is 28 m with floor height as 4m.
Calculate the base shear and shear distribution over the height of the building.
Answer:
- Design parameters:-
- For zone 3 building ,Z=0.16 table 2,IS 1893 part 1.
Importance factor I=1 table 6 IS:-1893 part 1
OMRF building response reduction factor R=table 7, IS 1893 part 1
3. Seismic weight:-
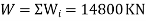
4. Fundamental time period:-
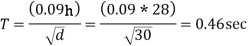
The building is located on type -2 9 (medium stiff soil)
From fig. 2 of IS; - 1893, part 1 for T = 0.46 sec
Sa/g=2.5
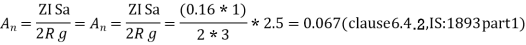
5. Design base shear:-
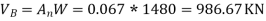
The design base shear is to be distributed with height as per clause 7.71, IS ;1893 , part 1
Story level | Wi | Hi |  |  |  |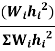
7 | 2114.29 | 28 | 1657.60 | 0.349 | 344.35 |
6 | 2114.29 | 24 | 121783 | 0.257 | 253.57 |
5 | 2114.29 | 20 | 845.72 | 0.179 | 176.61 |
4 | 2114.29 | 16 | 541.26 | 0.114 | 112.48 |
3 | 2114.29 | 12 | 304.46 | 0.064 | 63.15 |
2 | 2114.29 | 08 | 135.31 | 0.029 | 28.61 |
1 | 2114.29 | 04 | 33.83 | 0.007 | 6.91 |
 |
|
| 4736.01 | 1.000 | 986.67 |
