Unit – 1
Linear Differential Equations (LDE) and Applications
A differential equation is said to be linear if the dependent variable and its derivatives appears only in the first degree. The form of the linear differential equation of the first order is
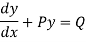
Where P & Q are functions of x or constant only.
A linear equation of the form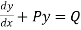 
is not solvable as it is.
However if we multiply it by the factor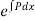 
it becomes exact & hence can be solved by the usual method.
To solve the equation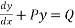 
:-
Multiply the given equation by the I.F.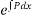 
, we get,
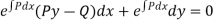
Since, it is exact, we have
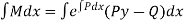
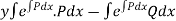
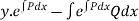
Since there is no term in N free from x, the solution is
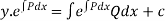
Remark :-To solve a linear differential equation, first write the equation with the coefficient of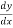
unity.
i.e. in the form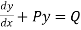 
Then find 
and further 
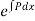
Then the solution is.
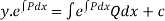
Solvesin2x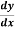
= y+tanx
Soln :-
The given equation can be written as,
which is a linear diff. eqn.
Now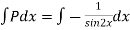 
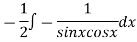
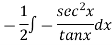
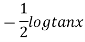
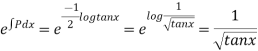
Thus the solution is.
= 
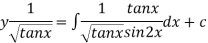
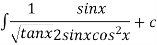
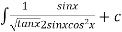
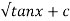
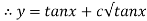
Which is the required solution.
Solve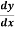
+ 
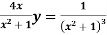
Soln :-
This is a linear differential equation
Consider
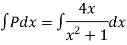
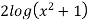
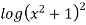
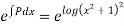
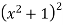
Hence, it’s solution is,
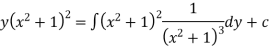
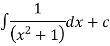
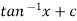
Exercise:
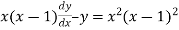
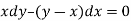
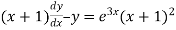
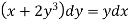
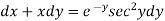
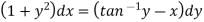
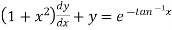
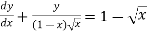
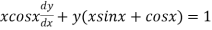
A differential equation of the form
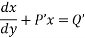
where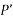 
&
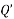are functions of y only is also a linear differential eqn with x & y having interchanged positions & Hence it’s solution is
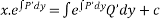
Solve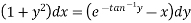 
Soln :-
The given eqn can be written as,
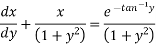
which is a linear diff eqn of the form
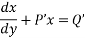
Now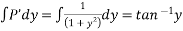 
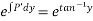
Hence it’s solution is
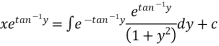
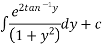
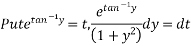
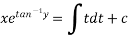
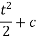
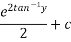
Thus
Is the required solution of given du=differential equation.
Solve(1 + x + xy2)dy + (y + y3)dx = 0
Soln :-
The given eqn can be written as,
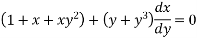
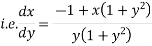
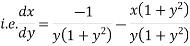
which is of the form,
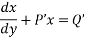
Now,
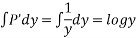
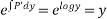
Hence solution is,
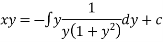
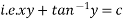
Component function: - different cases depending upon the nature of roots of the auxiliary equation .
If roots of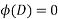 
be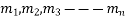 
all real & different, then the solution of 
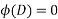will be
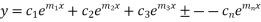
B. The case of real & repeated roots (multiple roots) :-
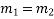
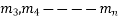
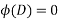
2. When three roots are repeated i.e if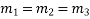 
are real & remaining roots 
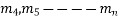are real & different then solution of 
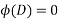is
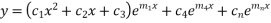
3. If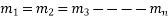 
i.e n roots real & different
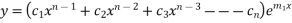
C. The case of imaginary (complex) roots
If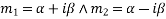 
D. The case of repeated imaginary roots
If the imaginary roots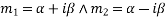
occur twice , then the part of solution of 
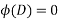will be
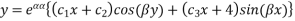
Particular integral function
By definition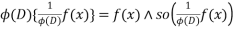 
Satisfies the eq.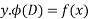 
& so is the P.I of the equation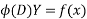 
Thus the P.I of the equation 
is symbolically given by
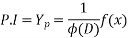
Methods of obtaining integral
This method involves integration
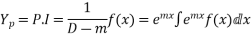
2. 
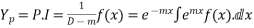
3. Put m=0
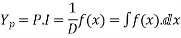
4. 
5. 
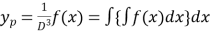
6. 
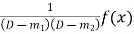
Que :-1 solve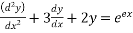 
Solution:- for C.F
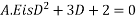
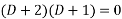
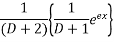
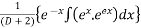( put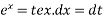 
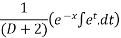
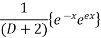
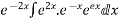
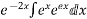
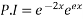
Hence the complete solution is
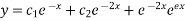
B. Short cut method
Formulae for ready reference
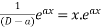
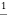
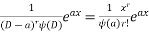
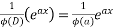
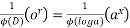
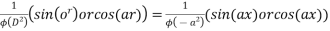
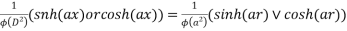
Note:- if denominator becomes zero after substitution then case of failure . resolve it by multiplying x & taking derivation of denominator.
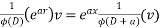
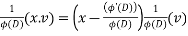
Que :-1 solve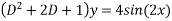 
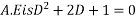
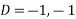
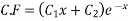
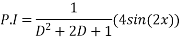
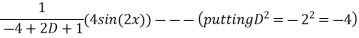
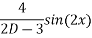
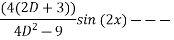
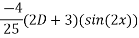
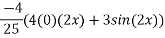
General solution is
Que :-2 solve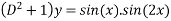 
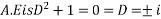
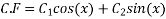
We have ,
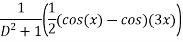
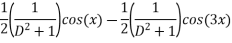
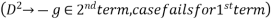
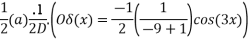
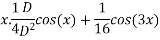
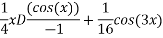
The general solution is
Que :- 3 solve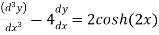 
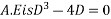
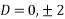
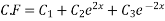
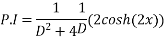
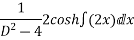
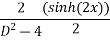
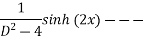
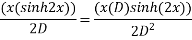
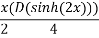
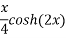
Solution is
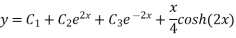
This method is used to solve the equation of the form
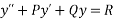
Where P,Q and R are functions of x only or constant.
Procedure: To find P.I. we will
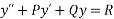
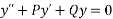
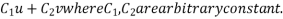
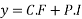
Here C.F 
Let P.I =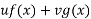
Where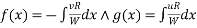 
And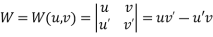 
Example1: Apply method of variation of parameter to solve
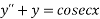
Given equation is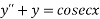 
Or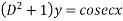 
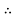The auxiliary equation is
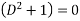
Or 
Then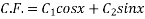 
Where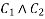 
are arbitrary constants.
Let P.I =
Where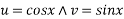 
Now ,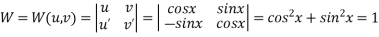 
Also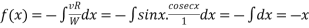 
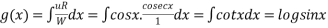
P.I =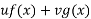
P.I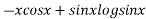 
Hence the general solution is
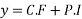
Is the required solution of the given equation.
Example2: Apply method of variation of parameter to solve
Given equation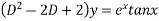 
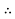The auxiliary equation is
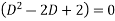
Or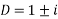 
Then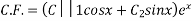 
Where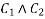 
are arbitrary constants.
Let P.I =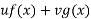
Where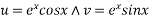 
Now ,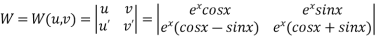 
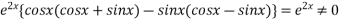
Also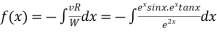 
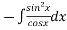
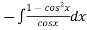
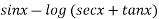
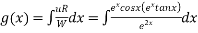
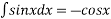
We have P.I =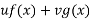
On substitution we get
P.I. =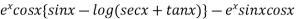 
Hence the general solution is
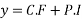
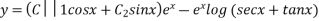
This is the required solution of the given equation.
Example3: Use the method of variation to solve
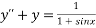
Given equation is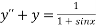 
Or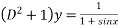 
Therefore the auxiliary equation is
Or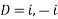 
Then C.F.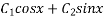 
Where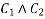 
are arbitrary constant.
Now, P.I =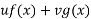
Where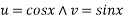 
Now ,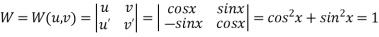 
Also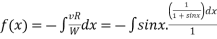 
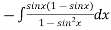
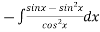
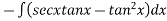
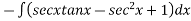
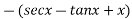
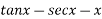
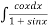
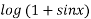
We have P.I =
On substitution we get
P.I. =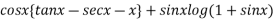 
Hence the general solution is
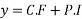
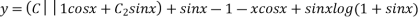
This is the required solution of the given equation.
A linear differential equation of the form
…(1)
Where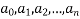 
are constant, and X is either a constant or a function of x only is called a Cauchy-Euler homogenous linear differential equation.
Rules to solve above equation is
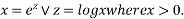
Where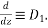 
c. Then (1) reduces to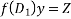 
..(2)
where Z is a function of z only.
d. The equation (2) will give the general solution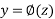 
.
e. Back Substitution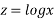 
.1w
Example1: Solve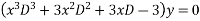 
Given equation is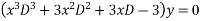 
Let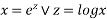 
Assume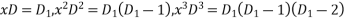 
Substituting in above equation we get
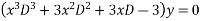
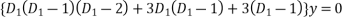
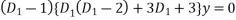
The auxiliary equation is
Or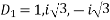 
Then solution is
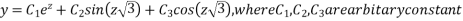
Or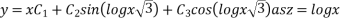 
This is the required solution of the given equation.
Example2: Solve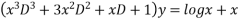 
Given equation is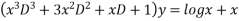 
Let 
Assume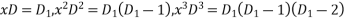 
Substituting in above equation we get
+
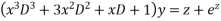
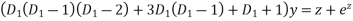
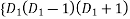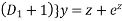
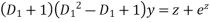
The auxiliary equation is
Or 
Then C.F.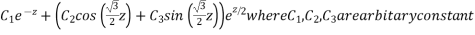 
= 
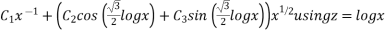
P.I.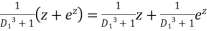 
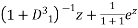
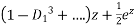
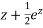
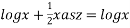
Hence the general solution is
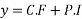
This is the solution of the given equation.
Example3: Solve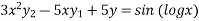 
Given equation can be re-write as
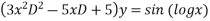
Let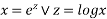 
Assume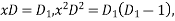 
Substituting in above equation we get
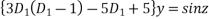
Or
Or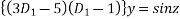 
The auxiliary equation is
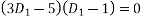
Or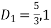 
Then C.F.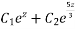 
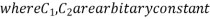
Or C.F. =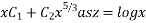 
P.I. =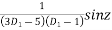 
(
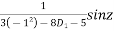
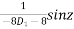
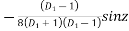
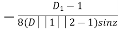
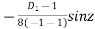
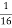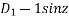
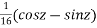
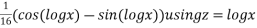
Hence the general solution is
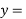
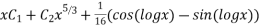
This is the required solution of the given equation.
A linear differential equation of the form
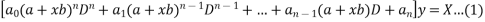
Where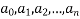 
are constant, and X is either a constant or a function of x only is called a Legendre’s linear differential equation.
Working Rule:
…………………
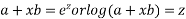
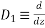
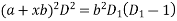
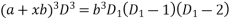
3. Then (1) reduces to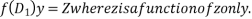 
4. We solve step (3) and get desired solution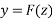 
5. Back Substitution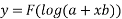 
Example1:Solve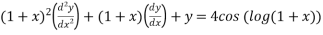 
Given equation can re-write
{
Let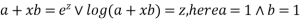 
Assume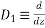 
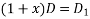
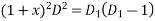
Substituting in above equation we get
{
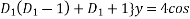(logz)
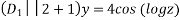
The auxiliary equation is
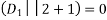
Or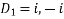 
Then C.F. 
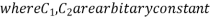
Or C.F.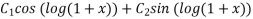 
Now, P.I.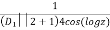 
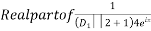
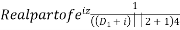
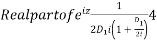
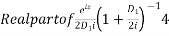
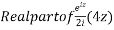
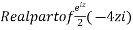
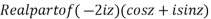
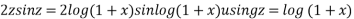
Hence the general solution is
+
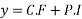
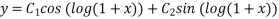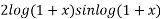
This is the required solution of the given equation.
Example2: Solve 
Given equation is
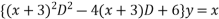
Let 
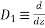
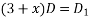
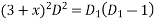
Substituting in above equation we get
The auxiliary equation is
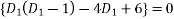
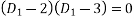
Or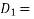 
2,3
Then C.F. 
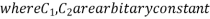
Or C.F.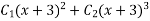 
Now, P.I. =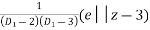 
= 
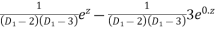
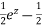
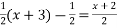
Hence the general solution is
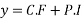
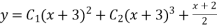
This is the required solution of the given equation.
1.8 simultaneous differential equation
que :-1 solve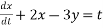 
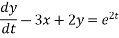
Writing in terms of operator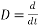 
we have
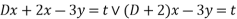----1
Solving for x (i.e eliminating y )
Operating 1 by (D+2 ) we have ,
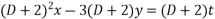
Or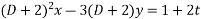 
---3
Multiplying eq 2 by 3 we get
Adding 3 and 4 we get
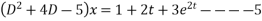
This is a linear differential equation with constant coeff.
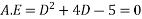
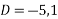
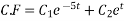
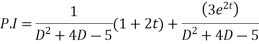
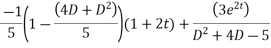
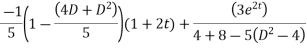
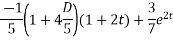
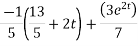
Hence the general solution for x is
Next general solution for (y)
Differentiating equation 6 with respect to t
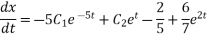
Putting value of x and dx/dt in equation 1 we get
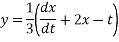
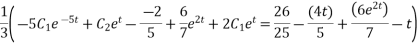
Simplifying we get
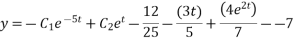
Hence equation 6 and 7 together are the general solutions
Symmetrical simultaneous differential equation
Defn:- equations of the type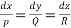 
Where P, Q , R are the functions of X,Y,Z are said to be symmetrical differential equation
Que 1 :- solve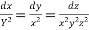 
Consider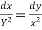 
Or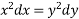 
By integrating both sides
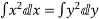
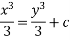
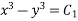—1
Which is the first solution
Now consider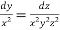 
Cancelling the common factor , we have
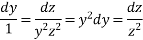
Integrate both sides we get
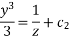
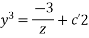
Equation 1 and 2 taken together constitute the answer
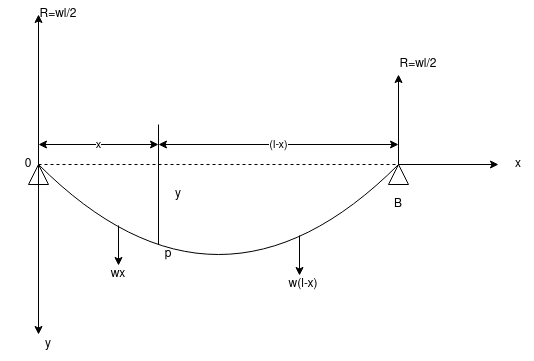
que 1 :- a horizontal simply supported uniform beam of length L bend under its own weight which is w kg per foot. Find the equation its elastic curve & max
1.6 Modelling of problems on bending of beams
Solution:- in above fig the elastic curve shown by thick line relative to a rectangular set of axis ox and oy with origin o.
Since the beam is simply supported to “o” & “b” each of this supports carry half the weight of beam and the beam equilibrium at the end.
Hence each reaction “R” is equal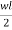 
and the bending moment of this force is acting at one side of pt “p”
If we 1st choose , the side left of “p” two forces are acting
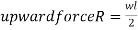
producing a- time moment to-
2. downward force= wx
producing time moment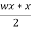 
the total bending movement at P
equation 1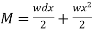 
but we know that
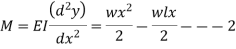
now integrate equation 2, we get
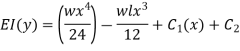
Since y=0 at x=0
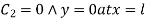
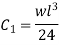
We have finally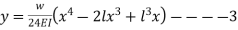 
The deflection y is maximum at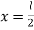 
Max deflection =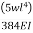
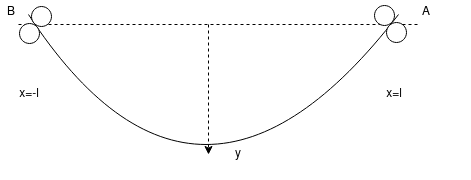
1.9 whirling of shafts and mass spring systems:-
que 1 :- the differential equation of a whirling of shaft , where w is the weight of the shaft & W its whirling speed is given by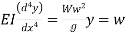 
taking the shaft of length 2l, with the origin at the center & short bearings at both ends , show that the medium deflection of the shaft is given by
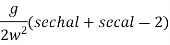
The given differential equation is
Where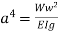 
C.F = A cos h(ax) + B sin (ax) + C cos(ax) +D sin (a)
& P.I =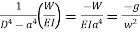
Hence the complete solution of 1 is
Y= A cos h (ax) + B sin h ( ax) + C cos (ax) + D sin (ax) –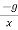
Differentiating we get ,
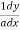=A sin h (ax) + B sin h (ax) -C sin (ax) + D sin (ax) ---3
= A cos h (ax) + B sin h (ax) -C cos (ax) -D sin ( ax) ---4
Since the end A is in short bearing
When x=l , y=0 &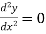 
From equation 2 and 4 we get
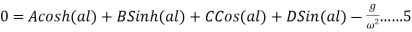
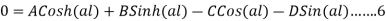
Similarly At end B
Where x=l & y=0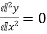 
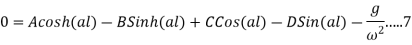
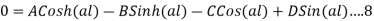
Adding equations 5, 7,6 & 8 we get
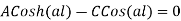
Hence
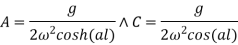
If we subtract equation 7 from 5 and 8 from 6 we get
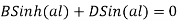from where we get B=0=D
& BSin(al)-DSin(al)=0
Now putting values of A,B,C & D in equation 2 we get,
And the Maximum deflection =Value of y at x=0
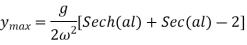
Reference Books
