Unit – 2
Numerical Methods
In this method we eliminate successively the unknown 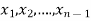 so that the equation (1) remain with the single unknown
so that the equation (1) remain with the single unknown 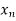 and reduce to upper triangular system. At last with help of back substitution we calculate the values of the remaining unknowns.
and reduce to upper triangular system. At last with help of back substitution we calculate the values of the remaining unknowns.
Consider a system of n linear equation in n unknown 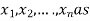
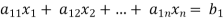
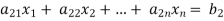
… …… ….. … (1)
… …… …. …
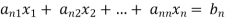
To convert the above system into upper triangular matrix we eliminate 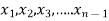 from the second, third, fourth …., n equations above by multiplying the first equation by
from the second, third, fourth …., n equations above by multiplying the first equation by 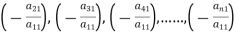 added them to the corresponding equations second, third, fourth,…., n equation. We get
added them to the corresponding equations second, third, fourth,…., n equation. We get
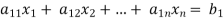
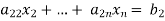
… …… ….. …
… …… …. …
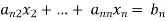
Repeating the above method for  we get finally the upper triangular form.
we get finally the upper triangular form.
Upper Triangular form of above

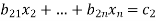
……………………….. (i)
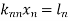
Thus 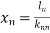 .
.
Then we calculate the values of 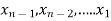 .
.
Example1 Apply Gauss Elimination method to solve the equations:
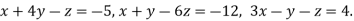
Given Check Sum (sum of coefficient and constant)
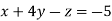 -1 …. (I)
-1 …. (I)
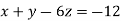 -16 …. (ii)
-16 …. (ii)
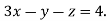 5 …. (iii)
5 …. (iii)
(I)We eliminate x from (ii) and (iii)
Apply eq(ii)-eq(i) and eq(iii)-3eq(i) we get
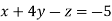 -1 ….(i)
-1 ….(i)
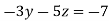 -15 ….(iv)
-15 ….(iv)
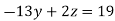 8 ….(v)
8 ….(v)
(II) We eliminate y from eq(v)
Apply 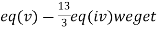
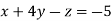 -1 ….(i)
-1 ….(i)
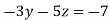 -15 ….(iv)
-15 ….(iv)
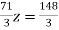 73 ….(vi)
73 ….(vi)
(III) Back Substitution we get
From (vi) we get 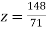
From (iv) we get 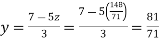
From (i) we get 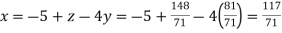
Hence the solution of the given equation is 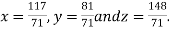
Example2 Solve the equation by Gauss Elimination Method:
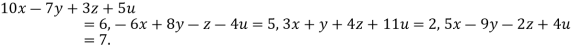
Given 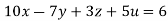
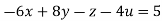
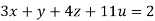
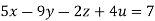
Rewrite the given equation as
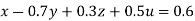 … (i)
… (i)
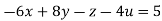 ….(ii)
….(ii)
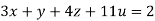 ….(iii)
….(iii)
 …(iv)
…(iv)
(I) We eliminate x from (ii),(iii) and (iv) we get
Apply eq(ii) + 6eq(i), eq(iii) -3eq(i), eq(iv)-5eq(i) we get
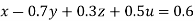 …(i)
…(i)
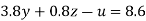 ….(v)
….(v)
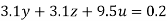 ….(vi)
….(vi)
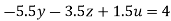 …(vii)
…(vii)
(II) We eliminate y from (vi) and (vii) we get
Apply 3.8 eq(vi)-3.1eq(v) and 3.8eq(vii)+5.5eq(v) we get
 …(i)
…(i)
 ….(v)
….(v)
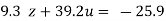 …(viii)
…(viii)
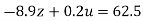 …(ix)
…(ix)
(III) We eliminate z from eq (ix) we get
Apply 9.3eq (ix) + 8.3eq (viii), we get
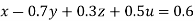 … (i)
… (i)
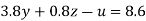 ….(v)
….(v)
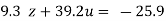 …(viii)
…(viii)
350.74u=350.74
Or u = 1
(IV) Back Substitution
From eq(viii) 
Form eq(v), we get 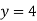
From eq(i) , 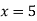
Hence the solution of the given equation is x=5, y=4, z=-7 and u=1.
Example3 Apply Gauss Elimination Method to solve the following system of equation:

Given 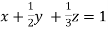 … (i)
… (i)
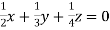 … (ii)
… (ii)
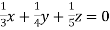 … (iii)
… (iii)
(I) We eliminate x from (ii) and (iii)
Apply 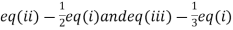 we get
we get
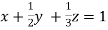 … (i)
… (i)
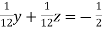 … (iv)
… (iv)
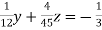 … (v)
… (v)
(II) We eliminate y from (v)
Apply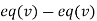 we get
we get
 … (i)
… (i)
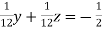 … (vi)
… (vi)
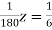 … (vii)
… (vii)
(III) Back substitution
From (vii) 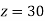
From (vi) 
From (i) 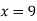
Hence the solution of the equation is 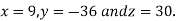
The Cholesky decomposition of a Matrix A is a decomposition of the form
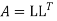
Where, L = Lower Triangular Matrix
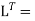 conjugate transpose of L
conjugate transpose of L
Working Rule to solve prroblems:
Step 1: 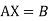
Step 2: 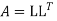
Step 3: 
Step 4: 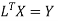
Consider
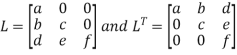
Que. Solve
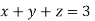
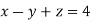
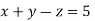
Solution. Step I. Consider AX= B
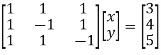
Step 2: Consider 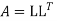
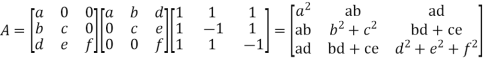
By solving
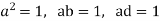
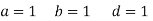
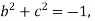
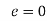 ,
, 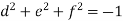
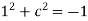
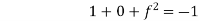


Put all the values
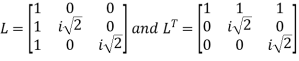
Step 3: LY = B, Let 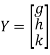
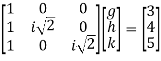
By multiplying and equating
g=3
and, 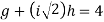
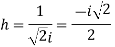
and, 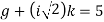


Therefore, 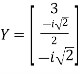
Step 4: 
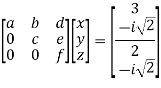
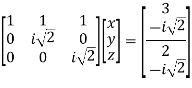
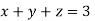
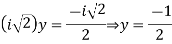

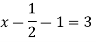
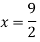
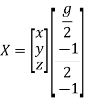
Now we are just cross check our Ans. by putting given equations of question
Given equation: 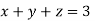
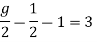


Our answer are correct
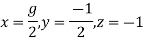
Que. Solve 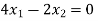
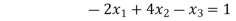
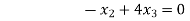
Solution. Step I. consider AX =B
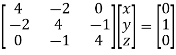
Step 2. Consider 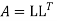
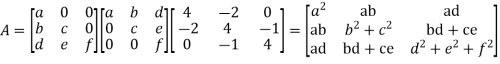
BY solving,
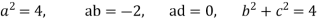


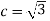



Put all the values we get
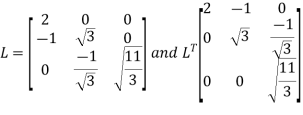
Step 3: LY = B, Let 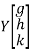
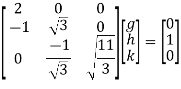
By multiplying and equating
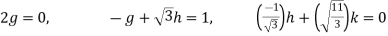

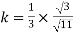

Step 4: 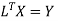
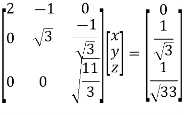
BY MULTIPLYING WE GET
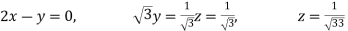
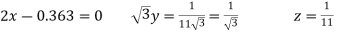
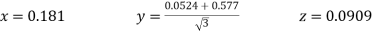
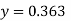
Now we are just cross check our ans by putting values in given equations of question,
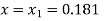
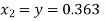
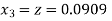
Given equation

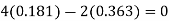
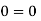
Our answer is correct.
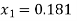
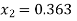
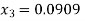
Que. Solve
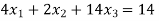
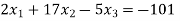
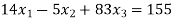
Solution. Step I Consider AX = B
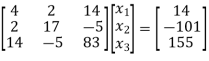
Step 2: Consider 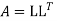
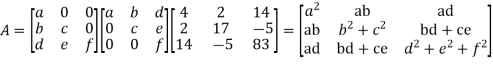
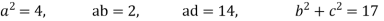



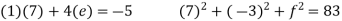



Put all the values we get
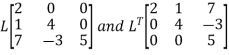
Step 3: 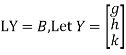
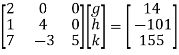
By multiplying and equating
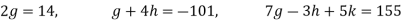



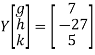
Step 4: 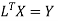
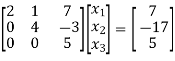
By multiplying we get
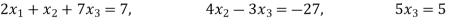
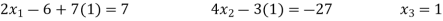



Now we are just cross check our answer by putting values of 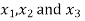 in equation
in equation
Given equation: 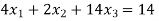
And we have 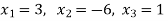
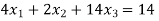
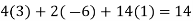
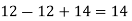


Our correct answer is
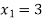
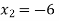
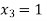
Que 4. Solve
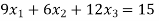
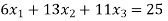
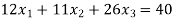
Solution. Step 1. Consider AX = B
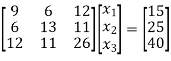
Step 2: Consider, 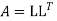
Let, 





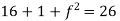
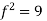
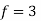
Put all the values we get
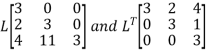
Step 3: LY = B, Let 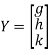
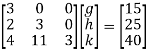
By multiplying and equating

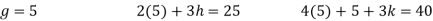



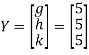
Step 4: 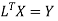

By Multiplying we get
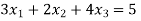

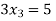
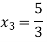
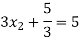

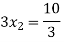
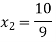
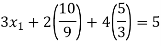
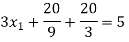

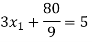
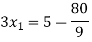
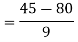
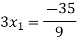
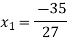
Now we just cross check our answer by putting values in given equation
Given equation: 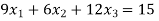
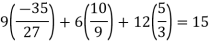

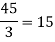
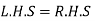
Final answer, 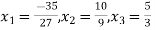
Jacobi’s Iteration method :
Let us consider the system of simultaneous linear equation
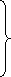

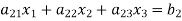 (1)
(1)
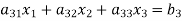
The coefficients of the diagonal elements are larger than the all other coefficients and are non-zero. Rewrite the above equation we get

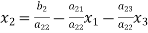 (2)
(2)
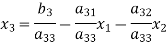
Take the initial approximation  we get the values of the first approximation of
we get the values of the first approximation of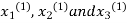 .
.
By the successive iteration we will get the desired the result.
Example1Use Jacobi’s method to solve the system of equations:
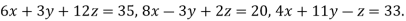
Since 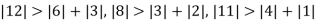
So, we express the unknown with large coefficient in terms of other coefficients.
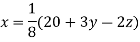
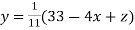 (1)
(1)

Let the initial approximation be 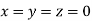
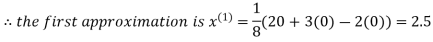
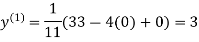
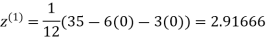
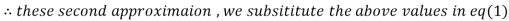

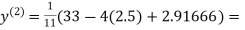 2.35606
2.35606
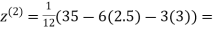 0.91666
0.91666
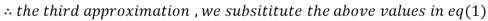


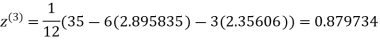
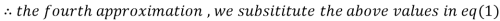
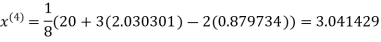
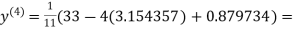 1.932936
1.932936
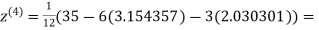 0.831912
0.831912

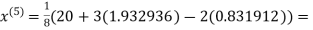 3.016873
3.016873
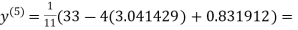 1.969654
1.969654
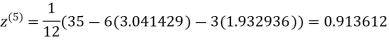
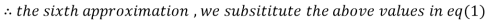
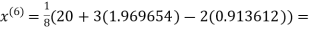 3.010217
3.010217
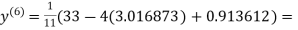 1.986010
1.986010
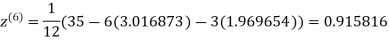

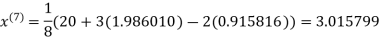
 1.988631
1.988631
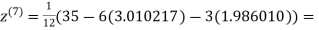 0.915055
0.915055
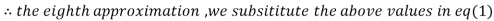
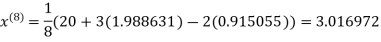
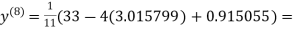 1.986532
1.986532
 0.911609
0.911609
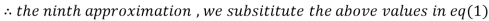
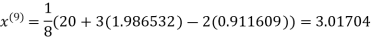
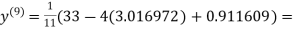 1.985792
1.985792
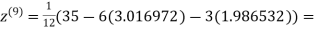 0.911547
0.911547
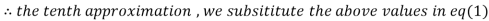
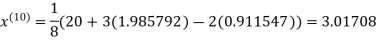
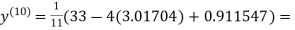 1.98576
1.98576
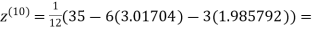 0.911698
0.911698
Since the approximation in ninth and tenth iteration is same up to three decimal places, hence the solution of the given equations is 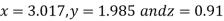
Example2 Solve by Jacobi’s Method, the equations
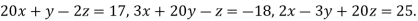
Given equation can be rewrite in the form
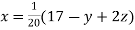 … (i)
… (i)
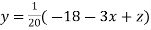 ..(ii)
..(ii)
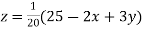 ..(iii)
..(iii)
Let the initial approximation be 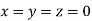
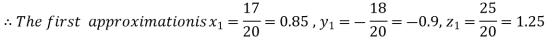
Putting these values on the right of the equation (i), (ii) and (iii) and so we get

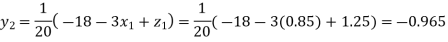
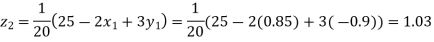
Putting these values on the right of the equation (i), (ii) and (iii) and so we get

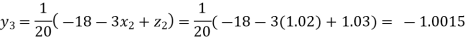
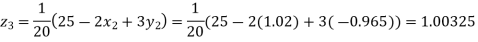
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
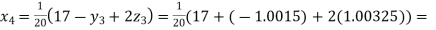 0.90025
0.90025
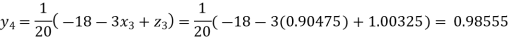
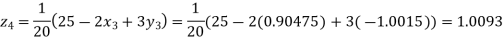
Putting these values on the right of the equation (i), (ii) and (iii) and so we get

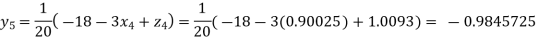
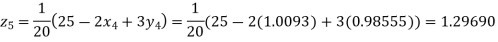
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
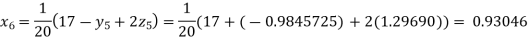
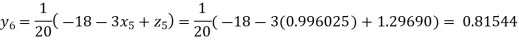
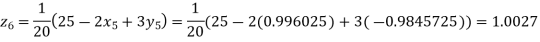
Hence solution approximately is 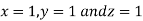
Example3Use Jacobi’s method to solve the system of the equations
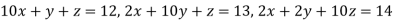
Rewrite the given equations
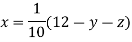
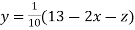 (1)
(1)
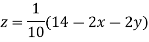
Let the initial approximation be 
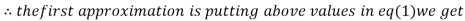
 1.2
1.2
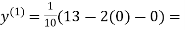 1.3
1.3
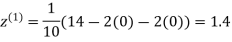
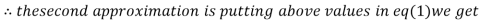
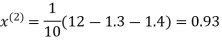
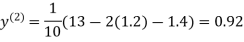
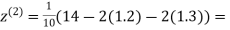 0.9
0.9

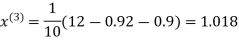
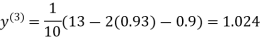
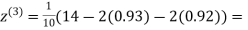 1.03
1.03

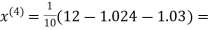 0.9946
0.9946
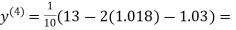 0.9934
0.9934
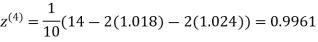

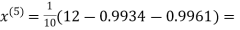 1.0015
1.0015
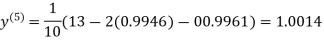
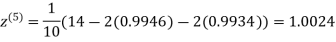
Hence the solution of the above equation correct to two decimal places is
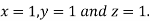
Gauss Seidel method:
This is the modification of the Jacobi’s Iteration. As above in Jacobi’s Iteration, we take first approximation as 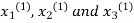 and put in the right hand side of the first equation of (2) and let the result be
and put in the right hand side of the first equation of (2) and let the result be 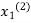 . Now we put
. Now we put 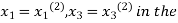 right hand side of second equation of (2) and suppose the result is
right hand side of second equation of (2) and suppose the result is 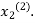 now put
now put 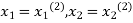 in the RHS of third equation of (2) and suppose the result be
in the RHS of third equation of (2) and suppose the result be 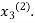 the above method is repeated till the values of all the unknown are found up to desired accuracy.
the above method is repeated till the values of all the unknown are found up to desired accuracy.
Example1 Use Gauss –Seidel Iteration method to solve the system of equations
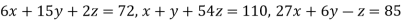
Since 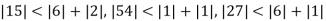
So, we express the unknown of larger coefficient in terms of the unknowns with smaller coefficients.
Rewrite the above system of equations
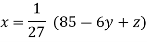
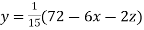 (1)
(1)

Let the initial approximation be 

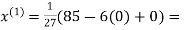 3.14814
3.14814
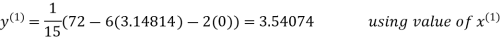
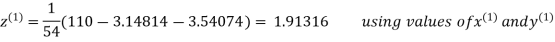
 2.43217
2.43217
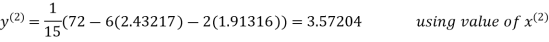
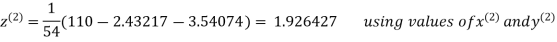

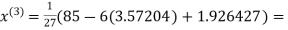 2.42571
2.42571
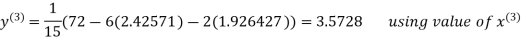
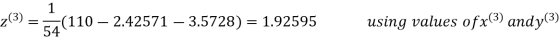
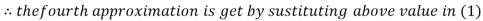
 2.4260
2.4260
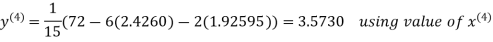
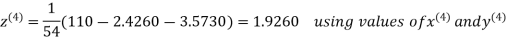
Hence the solution correct to three decimal places is
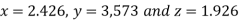
Example2 Solve the following system of equations
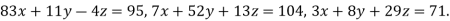 By Gauss-Seidel method.
By Gauss-Seidel method.
Rewrite the given system of equations as
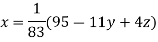
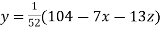 (1)
(1)
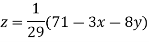
Le t the initial approximation be 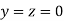

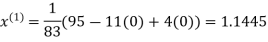
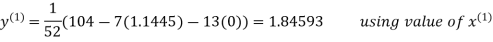
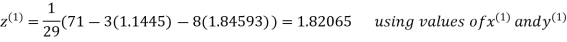
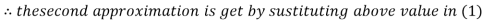
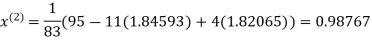
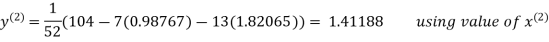
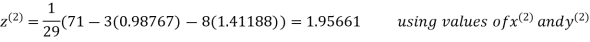
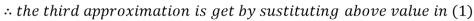
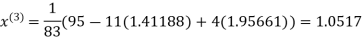
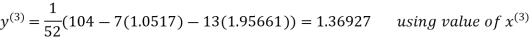
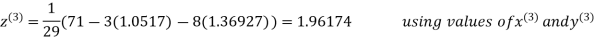
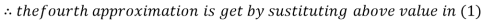
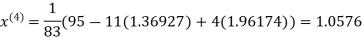
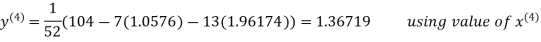

Thus the required solution is 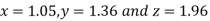
Example3 Solve the following equations by Gauss-Seidel Method

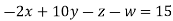

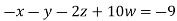
Rewrite the above system of equations

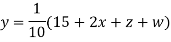
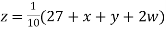 (1)
(1)
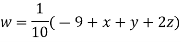
Let the initial approximation be 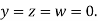


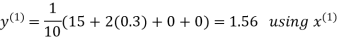
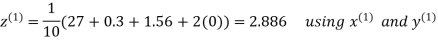
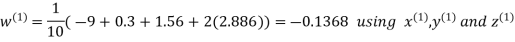

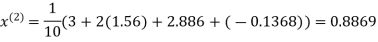
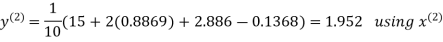
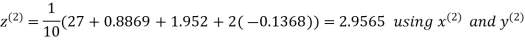
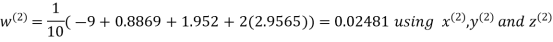

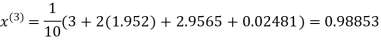
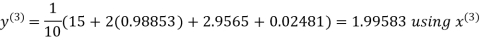
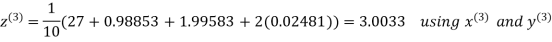
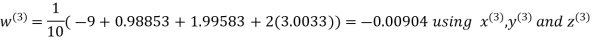


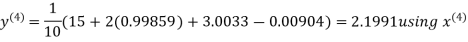

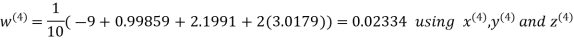

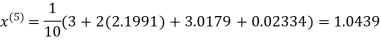
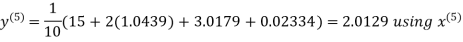
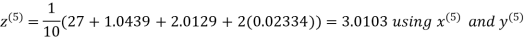
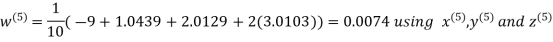
Hence the required solution is 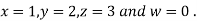
The general first order differential equation
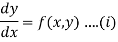
With the initial condition 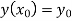
In this method the solution is in the form of a tabulated values.
Integrating both side of the equation (i) we get
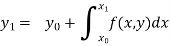
Assuming that 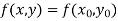 in
in 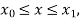 this gives Euler’s formula
this gives Euler’s formula

In general formula
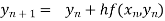 , n=0,1,2,…..
, n=0,1,2,…..
Error estimate for the Euler’s method
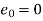
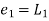

Example1:Use Euler’s method to find y(0.4) from the differential equation
 with h=0.1
with h=0.1
Given equation 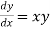
Here 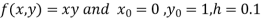
We break the interval in four steps.
So that 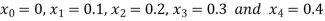
By Euler’s formula
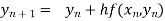 , n=0,1,2,3 ……(i)
, n=0,1,2,3 ……(i)
For n=0 in equation (i) we get
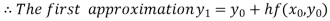
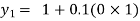
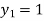
For n=1 in equation (i) we get
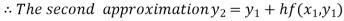
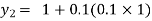
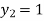 .01
.01
For n=2 in equation (i) we get

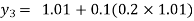
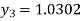
For n=3 in equation (i) we get
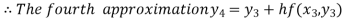
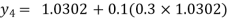
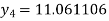
Hence y(0.4) =1.061106.
Example2:Using Euler’s method solve the differential equation for y at x=1 in five steps
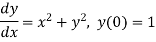
Given equation 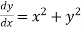
Here 
No. of steps n=5 and so that 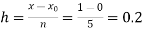
So that 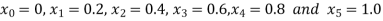
Also 
By Euler’s formula
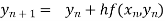 , n=0,1,2,3,4 ……(i)
, n=0,1,2,3,4 ……(i)
For n=0 in equation (i) we get
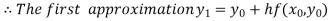
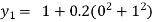

For n=1 in equation (i) we get
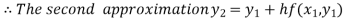
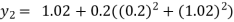
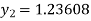
For n=2 in equation (i) we get
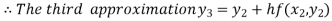
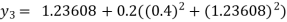
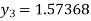
For n=3 in equation (i) we get
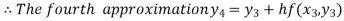
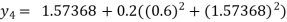
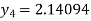
For n=4 in equation (i) we get
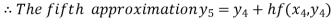

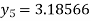
Hence 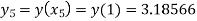
Example3:Given 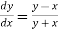 with the initial condition y=1 at x=0.Find y for x=0.1 by Euler’s method(five steps).
with the initial condition y=1 at x=0.Find y for x=0.1 by Euler’s method(five steps).
Given equation is 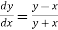
Here 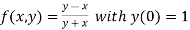
No. of steps n=5 and so that 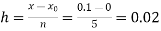
So that 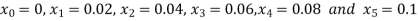
Also 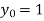
By Euler’s formula
 , n=0,1,2,3,4 ……(i)
, n=0,1,2,3,4 ……(i)
For n=0 in equation (i) we get
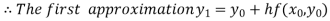
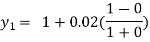
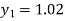
For n=1 in equation (i) we get
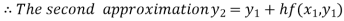

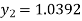
For n=2 in equation (i) we get
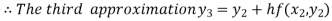
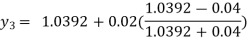
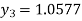
For n=3 in equation (i) we get
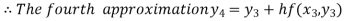


For n=4 in equation (i) we get
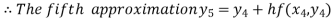

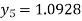
Hence 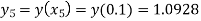
Instead of approximating 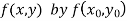 as in Euler’s method. In the modified Euler’s method we have the iteration formula
as in Euler’s method. In the modified Euler’s method we have the iteration formula
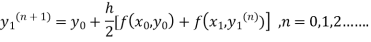
Where 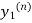 is the nth approximation to
is the nth approximation to 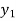 .The iteration started with the Euler’s formula
.The iteration started with the Euler’s formula
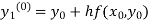
Example1:Use modified Euler’s method to compute y for x=0.05. Given that
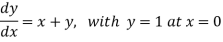
Result correct to three decimal places.
Given equation 
Here 
Take h = 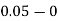 = 0.05
= 0.05
By modified Euler’s formula the initial iteration is
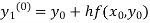
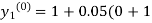 )
)
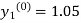
The iteration formula by modified Euler’s method is
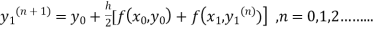 -----(i)
-----(i)
For n=0 in equation (i) we get
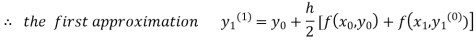
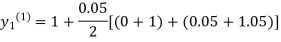
Where 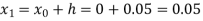 and
and 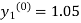 as above
as above
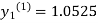
For n=1 in equation (i) we get


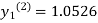
For n=3 in equation (i) we get
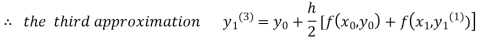
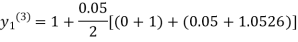
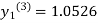
Since third and fourth approximation are equal .
Hence y=1.0526 at x = 0.05 correct to three decimal places.
Example2: Using modified Euler’s method , obtain a solution of the equation
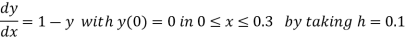
Given equation 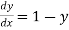
Here 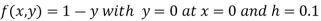
By modified Euler’s formula the initial iteration is
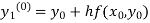
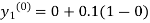
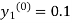
The iteration formula by modified Euler’s method is
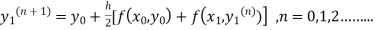 -----(i)
-----(i)
For n=0 in equation (i) we get
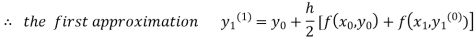

Where 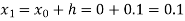 and
and 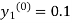 as above
as above
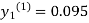
For n=1 in equation (i) we get
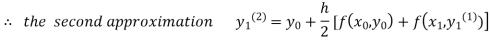
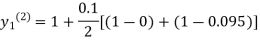
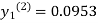
For n=2 in equation (i) we get
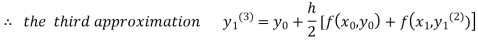
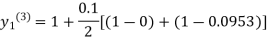
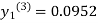
For n=3 in equation (i) we get
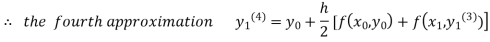
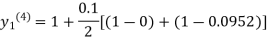
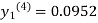
Since third and fourth approximation are equal.
Hence y=0.0952 at x=0.1
To calculate the value of 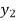 at x=0.2
at x=0.2
By modified Euler’s formula the initial iteration is
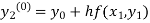

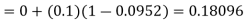
The iteration formula by modified Euler’s method is
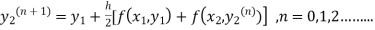 -----(ii)
-----(ii)
For n=0 in equation (ii) we get
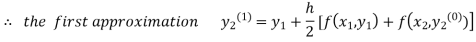
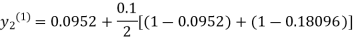
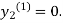 1814
1814
For n=1 in equation (ii) we get
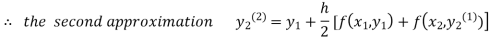
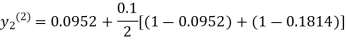
 1814
1814
Since first and second approximation are equal .
Hence y = 0.1814 at x=0.2
To calculate the value of  at x=0.3
at x=0.3
By modified Euler’s formula the initial iteration is

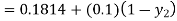
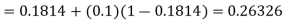
The iteration formula by modified Euler’s method is
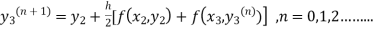 -----(iii)
-----(iii)
For n=0 in equation (iii) we get
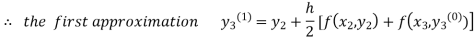
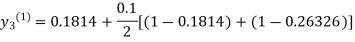
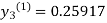
For n=1 in equation (iii) we get



For n=2 in equation (iii) we get
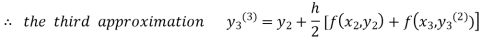
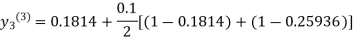
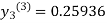
For n=3 in equation (iii) we get
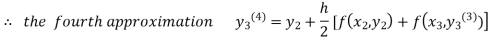
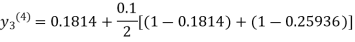
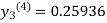
Since third and fourth approximation are same.
Hence y = 0.25936 at x = 0.3
This method is more accurate than Euler’s method.
Consider the differential equation of first order

Let 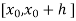 be the first interval.
be the first interval.
A second order Runge-Kutta formula
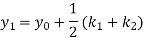
Where 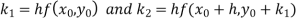
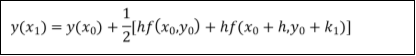 Rewrite as
Rewrite as
A fourth order Runge-Kutta formula:
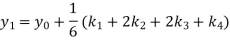
Where 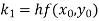
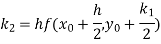
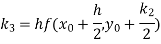
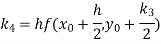
Example1: Use Runge-Kutta method to find y when x=1.2 in step of h=0.1 given that
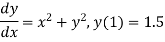
Given equation 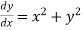
Here 
Also 
By Runge-Kutta formula for first interval
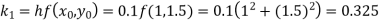
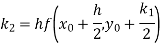
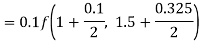

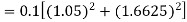
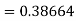
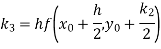
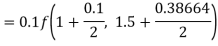

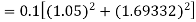
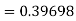
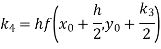
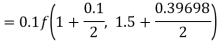
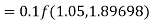
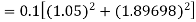
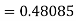
Again 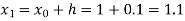
A fourth order Runge-Kutta formula:
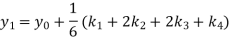


To find y at 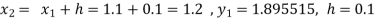
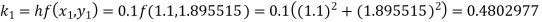
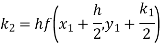
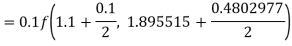
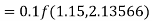
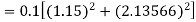
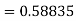
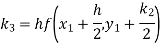
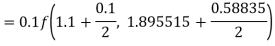
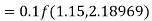
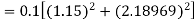
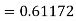
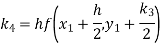
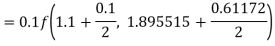
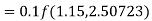
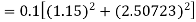
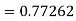
A fourth order Runge-Kutta formula:
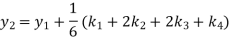

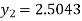
Example2: Apply Runge-Kutta fourth order method to find an approximate value of y for x=0.2 in step of 0.1, if
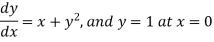
Given equation 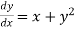
Here 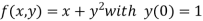
Also 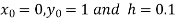
By Runge-Kutta formula for first interval
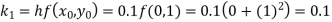


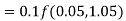
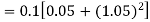

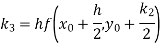
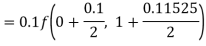
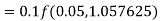
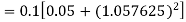
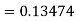
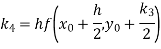
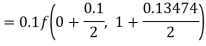
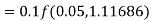
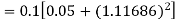
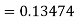
A fourth order Runge-Kutta formula:

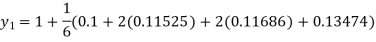
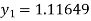
Again 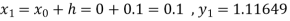
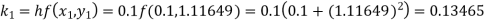
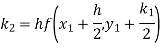

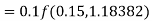
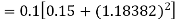
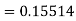
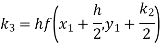

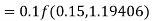

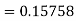
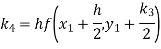

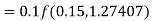
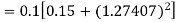
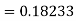
A fourth order Runge-Kutta formula:
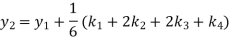

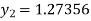
Example3: Using Runge-Kutta method of fourth order, solve

Given equation 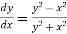
Here 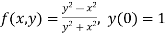
Also 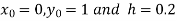
By Runge-Kutta formula for first interval
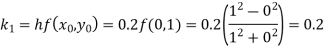
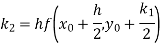
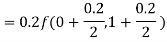
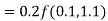
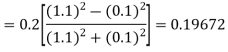
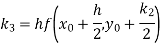
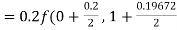 )
)

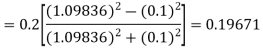
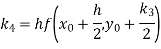

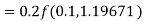

A fourth order Runge-Kutta formula:
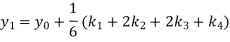
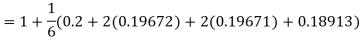
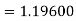
Hence at x = 0.2 then y = 1.196
To find the value of y at x=0.4. In this case 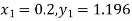

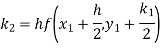
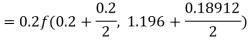
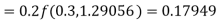
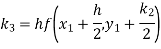
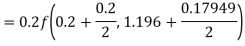
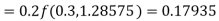
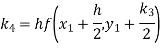

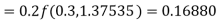
A fourth order Runge-Kutta formula:

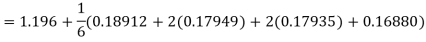

Hence at x = 0.4 then y=1.37527
Reference Books