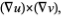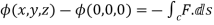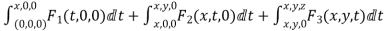Unit – 4
Vector Differential Calculus
In ordinary differentiate, the derivative 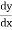 (where y=f(x)) is defined as
(where y=f(x)) is defined as 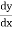 =
=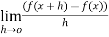
Consider vector 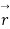 which may depend for its value on scular variable t. corresponding to change
which may depend for its value on scular variable t. corresponding to change 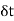 in t, let there be a change
in t, let there be a change 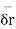 in
in 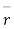 i.e
i.e
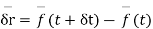
The vector derivative can now be defined as
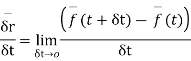
& we know that ,

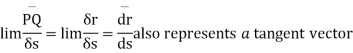
now 

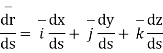
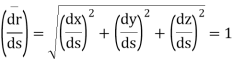
From the definition of vector derivative, following results can be easily established
For vector 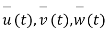
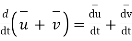
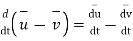
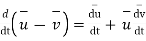
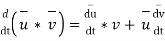
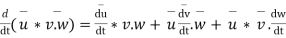
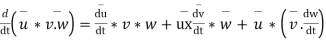

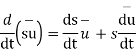
8. 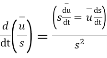
9. If S is constant 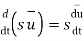
Application of mechanics in vector differentiate
Consider a particle P moving along a circle of radius r with constant angular. Speed w.
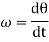
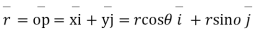
Differentiating 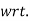 T
T
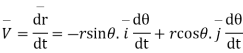
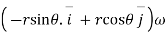
Again diff. we get ,
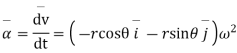
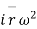
b. Radial & transverse component of velocity & acc
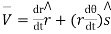
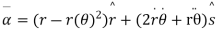
c tangential & normal component of Accn’s
tangential & normal component of Accn’s
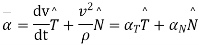
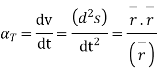
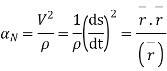
Que 1:- a curve is given by the equation 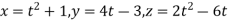 . Find the angle between tangents
. Find the angle between tangents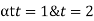 .
.
Solution :- 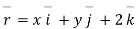
Where 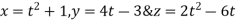
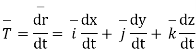
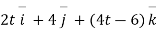
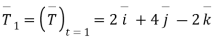
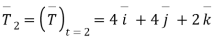
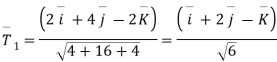
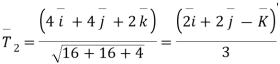
Now 
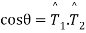


Que 2 if 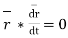 show that
show that 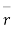 has a constant dim
has a constant dim
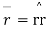

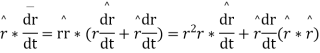
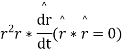
Now 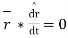
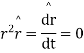
i.e 
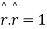
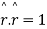
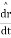
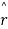
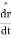
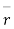
Both cant be true simultaneously

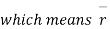 has constant direction.
has constant direction.
If cure 
i.e a vector field 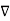 for which the curl vanishes.
for which the curl vanishes.
For a real-valued function f(x,y,z)f(x,y,z) on R3R3, the gradient ∇f(x,y,z)∇f(x,y,z) is a vector-valued function on R3R3 , that is, its value at a point (x,y,z)(x,y,z) is the vector
∇f(x,y,z)=(∂f/∂x,∂f/∂y,∂f/∂z)=∂f/∂xi+∂f/∂yj+∂f/∂zk
For example, it is often convenient to write the divergence div f as ∇⋅f∇⋅f, since for avectorfield f(x,y,z)=f1(x,y,z)i+f2(x,y,z)j+f3(x,y,z)kf(x,y,z)=f1(x,y,z)i+f2(x,y,z)j+f3(x,y,z)k, the dot product of f with ∇∇ (thought of as a vector) makes sense:
∇⋅f=(∂/∂xi+∂/∂yj+∂/∂zk)⋅(f1(x,y,z)i+f2(x,y,z)j+f3(x,y,z)k)
=(∂/∂x)(f1)+(∂/∂y)(f2)+(∂/∂z)(f3)
=∂f1/∂x+∂f2/∂y+∂f3/ ∂z
=div f
Let ϕ be a scalar point function and let ϕ(P) and ϕ(Q) be the values of ϕ at two neighboring points P and Q in the field. Then,
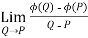
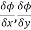 ,
,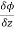 are the directional derivative of ϕ in the direction of the coordinate axes at P.
are the directional derivative of ϕ in the direction of the coordinate axes at P.
The directional derivative of ϕ in the direction l, m, n =l 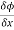 + m
+ m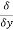 +
+ 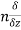
The directional derivative of ϕ in the direction of  =
= 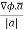
A solenoidal vector field satisfies
∇.B=0 |
|
for every vector  , where
, where 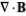 is the divergence. If this condition is satisfied, there exists a vector
is the divergence. If this condition is satisfied, there exists a vector 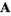 , known as the vector potential, such that
, known as the vector potential, such that
B=∇ X A |
|
where ∇ X A is the curl. This follows from the vector identity
∇. B=∇.(∇ X A) =0 |
|
If A is an irrotational field, then
A x r |
|
is solenoidal. If 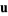 and
and 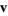 are irrotational, then
are irrotational, then
U x v |
|
is solenoidal. The quantity
|
|
Where  is the gradient, is always solenoidal.For a function
is the gradient, is always solenoidal.For a function 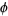 satisfying Laplace's equation
satisfying Laplace's equation
∇2ϕ=0 |
|
it follows that ∇ϕ is solenoidal (and also irrotational).
A vector field  for which the curl vanishes
for which the curl vanishes
A conservative vector field (for which the curl 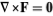 ) may be assigned a scalar potential
) may be assigned a scalar potential
\ |
where 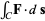 is a line integral.
is a line integral.
Q1. Calculate the curl for the following vector field.
F⃗ =x3y2 i⃗ +x2y3z4 j⃗ +x2z2 k⃗
Solution: In order to calculate the curl, we need to recall the formula.

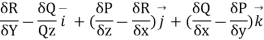
where P, Q, and R correspond to the components of a given vector field: F⃗ =Pi⃗ +Qj⃗ +Rk⃗
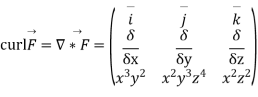
=( (x2z2)−
(x2z2)−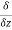 (x2y3z4) )i⃗ +(
(x2y3z4) )i⃗ +(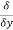 (x3y2)−
(x3y2)−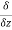 (xz2) )j⃗ +(
(xz2) )j⃗ +(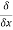 (x2y3z4)−
(x2y3z4)−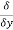 (x3y2) )k⃗
(x3y2) )k⃗
=(0−4x2y3z3)i⃗ +(0−2xz2)j⃗ +(2xy3z4−2x3y)k⃗
Thus the curl is
=(−4x2y3z3)i⃗ +(−2xz2)j⃗ +(2xy3z4−2x3y)k⃗
Q2. Find the directional derivative of Θ=x2y cos z at (1,2,π/2) in the direction of a = 2i+3j+2k.
Solution : ∇ϕ = i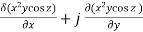 + k
+ k 
= 2xy cos zi+ x2 cos zj -x2y sin zk
At (1,2,π/2) ∇ϕ = 0i +0j-2k
Directional directive in the direction of 2i+3j+2k.
=(0i+0j-2k).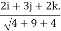 =-
=- 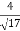
Q3. In what direction from the point (2,1,-1) is the directional derivative of ϕ=x2yz3 maximum? What is its magnitude?
Solution :∇ϕ= i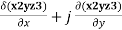 + k
+ k 
= -4i-4j+12k
Directional derivative is maximum in the direction of ∇Θ. Hence, directional derivative is maximum in the direction of -4i-4j+12k
Its magnitude =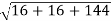 =4
=4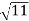
Example 4: Prove that ͞͞͞F = [y2 cos x +z3] i +(2y sin x – 4) j +(3xz2 + 2) k is a conservative field. Find (i) scalar potential for͞͞͞F (ii) the work done in moving an object in this field from (0, 1, -1) to (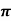 / 2,-1, 2)
/ 2,-1, 2)
 Sol. : (a) The field is conservative if cur͞͞͞͞͞͞F = 0.
Sol. : (a) The field is conservative if cur͞͞͞͞͞͞F = 0.
 Now, cur͞͞͞F =
Now, cur͞͞͞F = 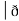 ̷̷
̷̷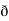 X
X  /
/ 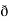 y
y 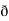 /
/ 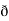 z
z
i j k
Y2COS X +Z3 2y sin x-4 3xz2 +2
; Cur 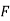 = (0-0) – (3z2 – 3z2) j + (2y cos x- 2y cos x) k = 0
= (0-0) – (3z2 – 3z2) j + (2y cos x- 2y cos x) k = 0
; F is conservative.
(b) Since F is conservative there exists a scalar potential ȸ such that
F = ȸ
 (y2 cos x +z3) i + (2y sin x-4) j + (3xz2 + 2) k
(y2 cos x +z3) i + (2y sin x-4) j + (3xz2 + 2) k
=  i +
i + 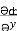 j +
j + 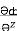 k
k
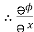 = y2 cos x + z3,
= y2 cos x + z3, 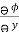 = 2y sin x – 4,
= 2y sin x – 4, 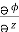 = 3xz2 + 2
= 3xz2 + 2
Now, 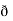 =
= 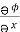 dx +
dx + 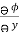 dy +
dy + 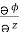 dz
dz
= (y2 cos x + z3) dx +(2y sin x – 4)dy + (3xz2 + 2)dz
= (y2 cos x dx + 2y sin x dy) +(z3dx +3xz2dz) +(- 4 dy) + (2 dz)
=d(y2 sin x + z3x – 4y -2z)
 ȸ = y2 sin x +z3x – 4y -2z
ȸ = y2 sin x +z3x – 4y -2z
(c) now, work done =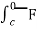 .d ͞r
.d ͞r
= 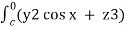 dx + (2y sin x – 4) dy + ( 3xz2 + 2) dz
dx + (2y sin x – 4) dy + ( 3xz2 + 2) dz
=  (y2 sin x + z3x – 4y + 2z) (as shown above)
(y2 sin x + z3x – 4y + 2z) (as shown above)
= [ y2 sin x + z3x – 4y + 2z ](  /2, -1, 2)
/2, -1, 2)
= [ 1 +8  + 4 + 4 ] – { - 4 – 2} =4
+ 4 + 4 ] – { - 4 – 2} =4 + 15
+ 15
Q5. If 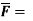 x2zi – 2y3z3j + xy2z2k find dvi
x2zi – 2y3z3j + xy2z2k find dvi 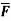 and curl
and curl  at (1,-1, 1)
at (1,-1, 1)
Solution : div 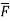 = ∇.
= ∇. =
= 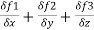 =
=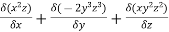
= 2xz – 6y2z3 + 2xy2z =(2-6+2) = -2

 Curl
Curl  =
= 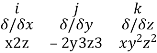
=i(2xyz2 + 6y3z2) – j(y2z2- x2) + k(0-0)
=-8 at (1,-1,1)
Q6. Find the angle between the normal to the surface xy = z2 at the points (1,4,2) and (-3,-3,3)
Solution: let ϕ = xy-z2
∇ϕ= i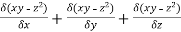 =yi + xj -2zk =4i + j -4k
=yi + xj -2zk =4i + j -4k
∇ϕ = 3i – 3j-6k
But these are the normal to the surface at given points. Angle between two vectors is given by (4i + j -4k).( 4i + j -4k)= |4i + j- 4k|.|-3i-3j -6K|cos θ.
If θ is the angle between then cos θ= 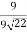 =
=  .
.
Questions
1. Find the directional derivative of 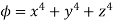 at point A(1,-2,1) in the direction of AB where B is
at point A(1,-2,1) in the direction of AB where B is
(2,6,-1).
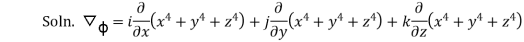

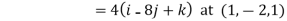
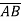 =
= 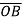 -
- 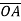 = (2-1)i + (6+2)j + (-1-1)k
= (2-1)i + (6+2)j + (-1-1)k
=I + 8j – 2k
Hence, Directional Derivative at A is the direction of 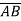 .
.
=4(i-8j+4k). 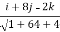 =
= 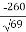
2. Find the directional derivative of 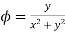 at (0,1) in direction making an angle of
at (0,1) in direction making an angle of 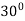 with positive
with positive
x axis.
Soln. Directional Derivative
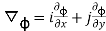
=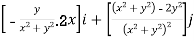
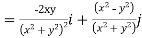
=0i-j at (0,1)
Unit vector making angle of  with axis
with axis
=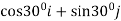
=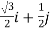
Hence, required directional derivative
=(0i-j). [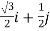 ] =
] =
3. Prove that 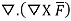 =0 where
=0 where 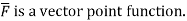
Soln. Let 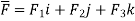

 Then,
Then, 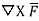 =
= 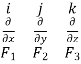

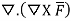 =
= ).[
).[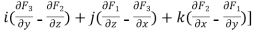
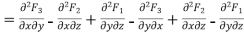
= 0
4. A vector field is given by 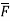 =
=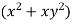 i + (
i + (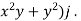 Show that
Show that 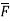 is irrotational and find its scalar potential.
is irrotational and find its scalar potential.

 Soln. Curl
Soln. Curl 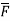 =
= 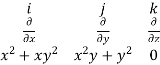
=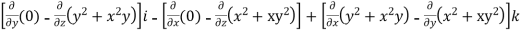
=0i+0j+(2xy-2xy)k
=0i+0j+0k
Hence,  is irrotational.
is irrotational.
If 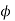 is the scalar potential, then
is the scalar potential, then 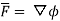
Therefore, 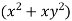 i + (
i + (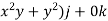 =
= 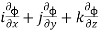
Comparing the coefficients of i , j , k
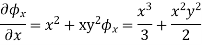


From above eq. common terms are:
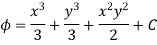
Q.5. Prove that 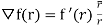 and hence find f if
and hence find f if 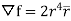 .
.
Soln. We have 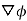 =
= 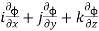
Here, 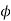 =f(r) and f is a function of r and r is a function of (x,y,z)
=f(r) and f is a function of r and r is a function of (x,y,z)
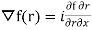 + j
+ j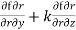
But 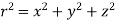
2r =2x
=2x
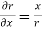 ,
, 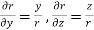
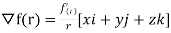
=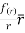
Comparing with 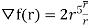 ; f(r)=
; f(r)= +C =
+C =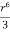
(2,6,-1).
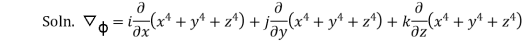
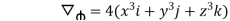
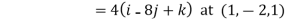
 =
=  -
- 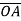 = (2-1)i + (6+2)j + (-1-1)k
= (2-1)i + (6+2)j + (-1-1)k
=I + 8j – 2k
Hence, Directional Derivative at A is the direction of 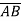 .
.
=4(i-8j+4k). 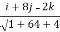 =
= 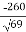
2. Find the directional derivative of 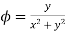 at (0,1) in direction making an angle of
at (0,1) in direction making an angle of 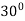 with positive
with positive
x axis.
Soln. Directional Derivative
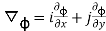
=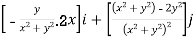
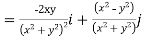
=0i-j at (0,1)
Unit vector making angle of 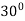 with axis
with axis
=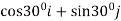
=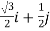
Hence, required directional derivative
=(0i-j). [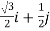 ] =
] =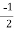
3. Prove that 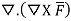 =0 where
=0 where 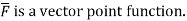
Soln. Let 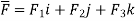

 Then,
Then, 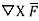 =
= 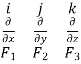

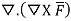 =
=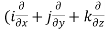 ).[
).[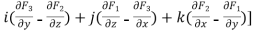

= 0
4. A vector field is given by  =
= i + (
i + (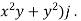 Show that
Show that 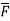 is irrotational and find its scalar potential.
is irrotational and find its scalar potential.

 Soln. Curl
Soln. Curl 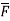 =
= 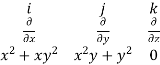
=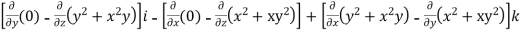
=0i+0j+(2xy-2xy)k
=0i+0j+0k
Hence, 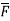 is irrotational.
is irrotational.
If 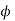 is the scalar potential, then
is the scalar potential, then 
Therefore, 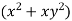 i + (
i + ( =
= 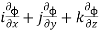
Comparing the coefficients of i , j , k
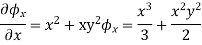


From above eq. common terms are:

Q.5. Prove that 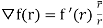 and hence find f if
and hence find f if 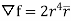 .
.
Soln. We have  =
= 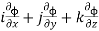
Here, 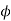 =f(r) and f is a function of r and r is a function of (x,y,z)
=f(r) and f is a function of r and r is a function of (x,y,z)
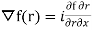 + j
+ j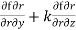
But 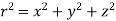
2r =2x
=2x
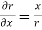 ,
, 
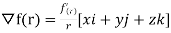
=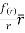
Comparing with 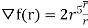 ; f(r)=
; f(r)=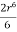 +C =
+C =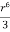
Reference Books