Unit – 5
Vector Integral Calculus and Applications
Let- F be vector function defined throughout some region of space and let C be any curve in that region. ṝis the position vector of a point p (x,y,z) on C then the integral ƪ F .dṝ is called the line integral of F taken over
Now, since ṝ =xi+yi+zk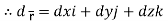
And if F͞ =F1i + F2 j+ F3 K
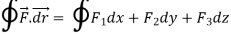
Q1. Evaluate 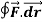 where F= cos y.i-x siny j and C is the curve y=
where F= cos y.i-x siny j and C is the curve y=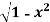 in the xy plae from (1,0) to (0,1)
in the xy plae from (1,0) to (0,1)
Solution : The curve y=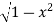 i.e x2+y2 =1. Is a circle with centre at the origin and radius unity.
i.e x2+y2 =1. Is a circle with centre at the origin and radius unity.
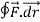 =
= 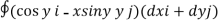
= 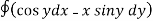
=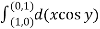 =-1
=-1
Q2. Evaluate 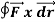 where
where 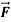 = (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).
= (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).
Solution : F x dr = 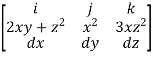
Put x=t, y=t2, z= t3
Dx=dt ,dy=2tdt, dz=3t2dt.
F x dr = 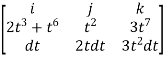
=(3t4-6t8) dti – ( 6t5+3t8 -3t7) dt j +( 4t4+2t7-t2)dt k
=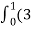 t4-6t3)dti –(6t5+3t8-3t7)dt j+(4t4 + 2t7 – t2)dt k
t4-6t3)dti –(6t5+3t8-3t7)dt j+(4t4 + 2t7 – t2)dt k
=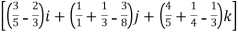
=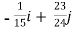 +
+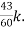
Example 4: Prove that ͞͞͞F = [y2 cos x +z3] i+(2y sin x – 4) j +(3xz2 + 2) k is a conservative field. Find (i) scalar potential for͞͞͞F (ii) the work done in moving an object in this field from (0, 1, -1) to (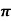 / 2,-1, 2)
/ 2,-1, 2)
 Sol. : (a) The fleld is conservative if cur͞͞͞͞͞͞F = 0.
Sol. : (a) The fleld is conservative if cur͞͞͞͞͞͞F = 0.
 Now, curl͞͞͞F =
Now, curl͞͞͞F = 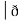 ̷̷
̷̷ X
X  /
/ 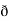 y
y 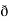 /
/ 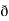 z
z
Y2COS X +Z3 2y sin x-4 3xz2 + 2
; Cur  = (0-0) – (3z2 – 3z2) j + (2y cos x- 2y cos x) k = 0
= (0-0) – (3z2 – 3z2) j + (2y cos x- 2y cos x) k = 0
; F is conservative.
(b) Since F is conservative there exists a scalar potential ȸ such that
F = ȸ
 (y2 cos x=z3) i + (2y sin x-4) j + (3xz2 + 2) k =
(y2 cos x=z3) i + (2y sin x-4) j + (3xz2 + 2) k = 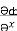 i +
i + 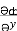 j +
j + 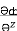 k
k
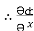 = y2 cos x + z3,
= y2 cos x + z3, 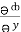 = 2y sin x – 4,
= 2y sin x – 4, 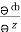 = 3xz2 + 2
= 3xz2 + 2
Now, 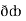 =
= 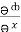 dx +
dx +  dy +
dy + 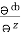 dz
dz
= (y2 cos x + z3) dx +(2y sin x – 4)dy + (3xz2 + 2)dz
= (y2 cos x dx + 2y sin x dy) +(z3dx +3xz2dz) +(- 4 dy) + (2 dz)
=d(y2 sin x + z3x – 4y -2z)
 ȸ = y2 sin x +z3x – 4y -2z
ȸ = y2 sin x +z3x – 4y -2z
(c) now, work done =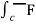 .d ͞r
.d ͞r
= 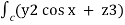 dx + (2y sin x – 4) dy + ( 3xz2 + 2) dz
dx + (2y sin x – 4) dy + ( 3xz2 + 2) dz
= 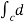 (y2 sin x + z3x – 4y + 2z) (as shown above)
(y2 sin x + z3x – 4y + 2z) (as shown above)
= [ y2 sin x + z3x – 4y + 2z ]( 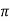 /2, -1, 2)
/2, -1, 2)
= [ 1 +8  + 4 + 4 ] – { - 4 – 2} =4
+ 4 + 4 ] – { - 4 – 2} =4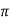 + 15
+ 15
Sums Based on Line Integral
1. Evaluate 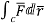 where
where 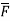 =yz i+zx j+xy k and C is the position of the curve.
=yz i+zx j+xy k and C is the position of the curve.
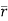 = (a cost)i+(b sint)j+ct k , from y=0 to t=π/4.
= (a cost)i+(b sint)j+ct k , from y=0 to t=π/4.
Soln.  = (a cost)i+(b sint)j+ct k
= (a cost)i+(b sint)j+ct k
The parametric eqn. of the curve are x= a cost, y=b sint, z=ct (i)
 =
=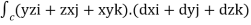
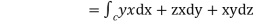
Putting values of x,y,z from (i),
dx=-a sint
dy=b cost
dz=c dt
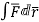 =
=
=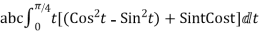
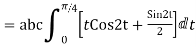
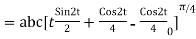
=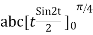 =
= 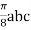
2. Find the circulation of 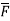 around the curve C where
around the curve C where 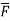 =yi+zj+xk and C is circle
=yi+zj+xk and C is circle  .
.
Soln. Parametric eqn of circle are:
x=a cos
y=a sin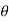
z=0
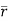 =xi+yj+zk = a cos
=xi+yj+zk = a cos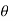 i + b cos
i + b cos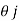 + 0 k
+ 0 k
d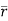 =(-a sin
=(-a sin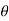 i + a cos
i + a cos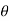 j)d
j)d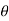
Circulation =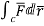 =
=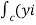 +zj+xk). d
+zj+xk). d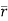
=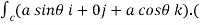 -a sin
-a sin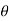 i + a cos
i + a cos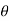 j)d
j)d
=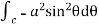 =
= 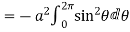
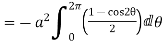


The surface integral of a vector point function  over a surface S is defined as the integral of the normal component of
over a surface S is defined as the integral of the normal component of 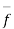 taken over the surface S.
taken over the surface S.
Consider surface S as shown in fig.
Let 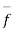 act at p enclosed by an element of area
act at p enclosed by an element of area 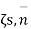 is a unit vector normal to the surface at P. normal component of
is a unit vector normal to the surface at P. normal component of  is given by
is given by 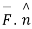
The surface integral can be expressed as
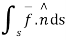 or
or 
If we write 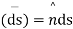 , then the above integral is also be written as
, then the above integral is also be written as
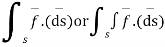
Q1. Find the work done in moving a particle once round the complete circle x2+y2=a2 , z=0 in the force filed given by 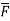 = sin yi +(x + x cos y )j.
= sin yi +(x + x cos y )j.
Solution: work done= 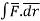 =
= 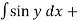 (x+x cos y )dy
(x+x cos y )dy
Using parametric equation x=a cos θ, y=a sinθ
Work done =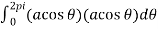
=  .
.
If P and Q are two functions of x, y and their partial derivatives 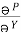 ,
,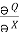 are continuous single valued functions over the closed region bounded by a curve C then
are continuous single valued functions over the closed region bounded by a curve C then
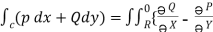 } dx dy.
} dx dy.
EXAMPLE – 1 Verify green’s theorem for  and C is the triangle having verticles A (0,2 ) , B (2,0 ) , C (4,2 ).
and C is the triangle having verticles A (0,2 ) , B (2,0 ) , C (4,2 ).
SOLUTION : By green theorem.

Here ,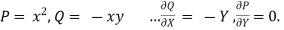
(a) Along AB , since the equation of AB is
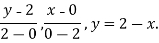
Putting 
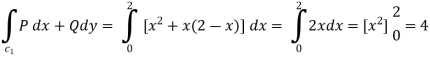
Along BC , since the equation of BC , 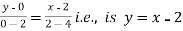 .
.
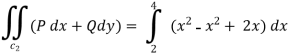
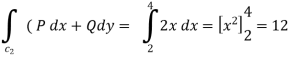
Along CA , since the equation of CA, is y = 2 , dy = 0.
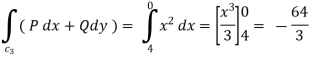
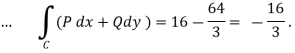
(b) 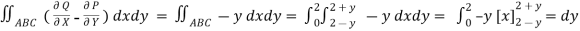
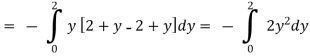
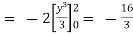 .
.
From (1) and (2) , the theorem is verified .
Example 2 :Evaluate by Green ‘s theorem 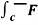 = - xy (xi –yj) and c is r= a (1+ cos
= - xy (xi –yj) and c is r= a (1+ cos 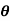 )
)
Sol : By Green’s Theorem , 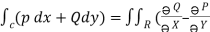 ) dx dy
) dx dy
Now,  .dṝ =
.dṝ = 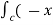 2yi + xy2 j ) . (d xi + dy j) =
2yi + xy2 j ) . (d xi + dy j) =  2y dx + xy2dy )
2y dx + xy2dy )
By comparison p= - x2y, Q = xy2
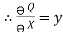 2,
2, 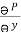 = - x2
= - x2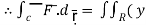 2 + x2) dx dy
2 + x2) dx dy
To evaluate the integral , we put x = r cos 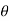 , y = r sin
, y = r sin 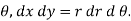 for the cardioid r = a ( 1 + cos
for the cardioid r = a ( 1 + cos 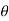 ), we take the integral from
), we take the integral from 
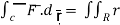 2 .rdr d
2 .rdr d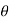 = 2
= 2 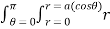 3dr d
3dr d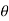
= 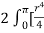 ]a ( 1 + cos
]a ( 1 + cos 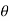 ) dθ =
) dθ = 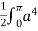 (1+ cos θ)4dθ
(1+ cos θ)4dθ
=8a4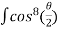 =
= 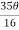 a4
a4
Example Based on Green’s Theorem
1. Verify Green’s Theorem in the plane for 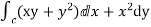 where C is the closed curve of region bounded by y=x and y=
where C is the closed curve of region bounded by y=x and y=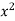 .
.
Soln. By Green’s Theorem,
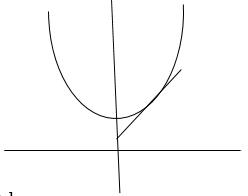
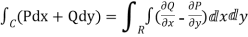 A(1,1)
A(1,1)
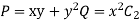 y=x
y=x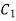 y=
y=
 B
B
(a) Along  , y=
, y=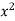 and dy=2x dx and x varies from 0 to 1.
and dy=2x dx and x varies from 0 to 1.

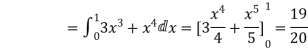
 Along
Along  y=x and dy=dx and x varies from 1 to 0.
y=x and dy=dx and x varies from 1 to 0.
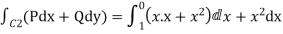
=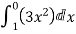
=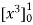 = 1
= 1
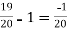 = L.H.S.
= L.H.S.
RHS=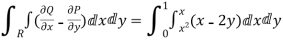
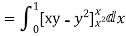
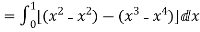
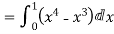

The divergence theorem states that the surface integral of the normal component of a vector point function “F” over a closed surface “S” is equal to the volume integral of the divergence of F⃗ taken over the volume “V” enclosed by the surface S. Thus, the divergence theorem is symbolically denoted as:
∬v∫▽F⃗ .dV=∬sF⃗ .n⃗ .dS
Sums on surface and volume
EXAMPLE – 1 Use divergence theorem to show that 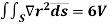 where Sisanyclosed surface enclosing a volume V.
where Sisanyclosed surface enclosing a volume V.
SOLUTION: By divergence theorem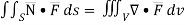
Here ,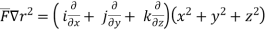
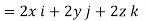
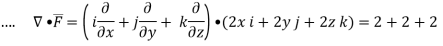
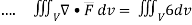 = 6V
= 6V
EXAMPLE – 2Show that 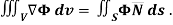
SOLUTION: By divergence theorem, 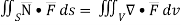 ..…(1)
..…(1)
Comparing this with the given problem let
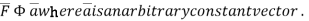
Hence, by (1)
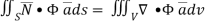 ………….(2)
………….(2)
Now ,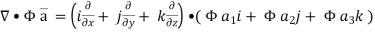
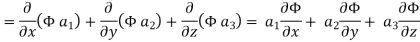
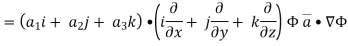
Hence,from (2),Weget,
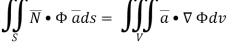
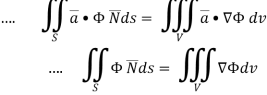
Example Based on Gauss Divergence Theorem


Soln. We have Gauss Divergence Theorem
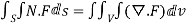
By data, F=
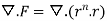
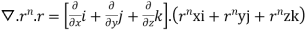
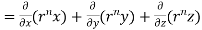
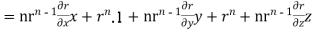
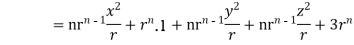
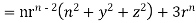
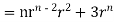
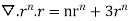
=(n+3)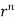

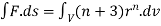
2 Prove that  =
=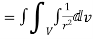
Soln. By Gauss Divergence Theorem,
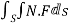 =
=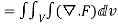
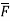 =
= =
=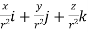
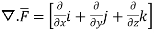 .[
.[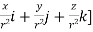
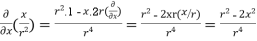
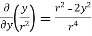

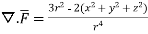 =
= 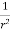
The integral of the normal component of the curl of a vector F͞ over a surface S is equal to the line integral of the tangential component of F͞ around the curve bounding S i.e
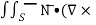 F͞ )ds =
F͞ )ds =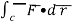
Q1.Use stoke’s theorem to evaluate 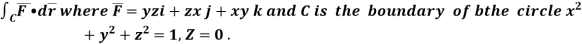
SOLUTION : We have by stoke’s theorem 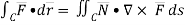
Now ,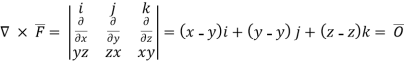
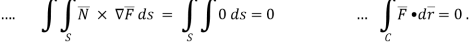
Applications to problems in fluid mechanics are mainly in
- STREAMLINES
- EQUATION OF CONTINUITY
- BERNOULLI’S EQUATION
- EQUATION OF MOTION
applications of vectors and fluid mecahnies
5.8 streamlines
Definition:-an imaginary curve drawn in the fluid such that at any instant of time, the tangent at any point of it is along the velocity vector at the point is called stream line.
Stream line indicates the dim of motion at each as shown in fig. from the definition it is clear that these can be no flaw area a stream line
To find the equation of stream line , consider two points 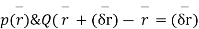 on the stream line .
on the stream line .
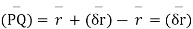
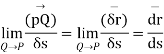
Represent unit tangent vector F at P .
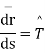
Let  be velocity vector at P.
be velocity vector at P.
From the definition , (k is some constant)
(k is some constant)
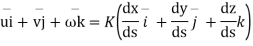
Equating 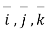 component , we get
component , we get
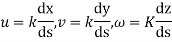
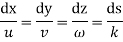
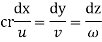
represents the diffential equation of stream line
question 1 :- velocity distribution for a fluid flow is given by
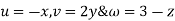 find the equation of
find the equation of
Stream line passing through the point (1,1,2)
Ans:- the diffential equation of stream line are given by
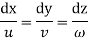
Putting for u,v,w we get
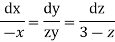
These are two independent equations, consider
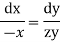
Integrating 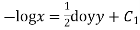 -------1
-------1
As stream the passes through (1,1,2)
Put x=1 , y=1 in eq. 1
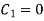
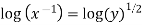
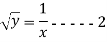
Consider now, 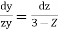
Integrating gives , 
Putting 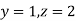 we get
we get 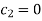
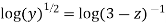

Equation 2 &4 together represent curve of intersection of surface
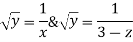
Which represents the stream line
Question 2:- if the velocity of an incompressible fluid at (x,y,z) is given by
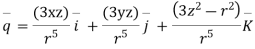
Where 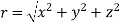
Then determine the stream line at motion
Answer:- equation of stream lines are given by

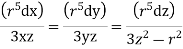

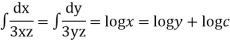
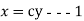
Similarly
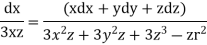

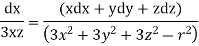
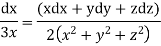
Integrating , 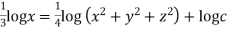
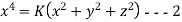
Eq 1 & 2 together represents stream line
Equation of continuity is the expression of the law of constellation of energy
Let S be the closed surface drawn in the fluid & taken fixed in a space. suppose it encloses a volume v at the fluid.
Let 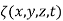 be the fluid density.
be the fluid density.
Let 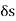 be the surface element &
be the surface element & 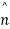 be the unit outward drawn normal to
be the unit outward drawn normal to 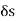 .
.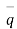 is the fluid velocity at
is the fluid velocity at 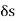
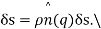
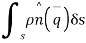
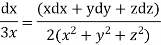
integrating 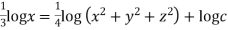
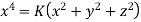
Equation 1 & 2 together represents stream line
Using Gauss divergence theorem
Total rate of mass flow= 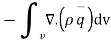
At time t , the mass of fluid with the element is 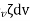
Rate of increase of mass with V =
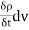
For conservation we have
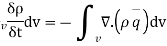
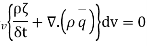
Valid for all volume V,
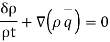
Which is called equation of continuity in cartesion form,
Equation of continuity
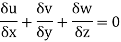
we know that Euler’s equation of motion as
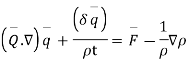
Now tell us consider following conditions:-
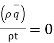
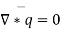
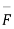
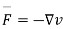 ( v is for potential)
( v is for potential)
Using vector identify results , we can write

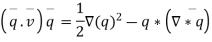
But 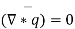 ( motion is imtational)
( motion is imtational)
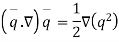
Euler’s equation of motion now takes the form
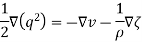
Taking dot product with 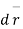 we get
we get
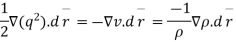
But dv=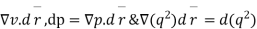
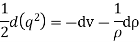
Integrating above equation
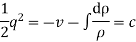
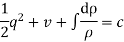
Eq. is called Bernoulli’s equation
Que :-1 given the velocity fields

What is the acceleration of a particle at (3,0,2) at time t=1
Ans :- we have u=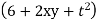 , V =
, V = 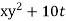 , W =25
, W =25
The component is given by


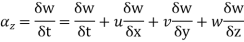
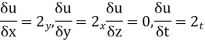
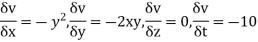
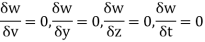
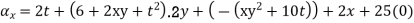

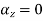
Substituting x=3, y=0 & z=2 &t=1
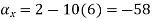
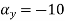

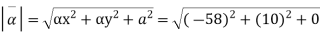

Question 2:- a liquid is in equilibrium under the action of field 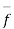 per unit mass given by
per unit mass given by
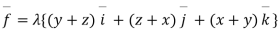
Find the pressure at any point on the field
Answer :- let v be the force potential
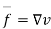
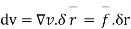
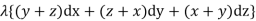
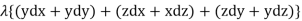
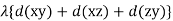
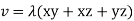
From the Bernoullis eq
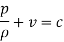
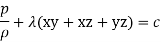
Which gives pressure at any point
Reference Books