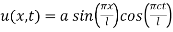Unit – 6
Applications of Partial Differential Equations (PDE)
Differential equation in which partial derivatives one involved, are called partial differential equation (PDE).
The order of the PDE is the highest order of partial derivatives presenting it.
We know that,
Partial differential equation of order one obtained by eliminating one arbitrary function 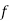 .
.
Having two order obtained by eliminating two arbitrary function 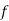 and .
and .
While deriving a differential equation corresponding to a string problem we assume the following assumptions.
The string is perfectly plastic and doesn’t offer any resistance to bending.
The mass of the string per unit length is constant.
The tension is so large.
Consider the forces acting on a small portion of string. Let T1 and T2 be the tensions at end P and Q.
The horizontal components of T1 and T2 must be constant.
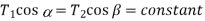 (1)
(1)
and vertical components of 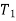 and
and 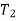 are
are 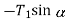 and
and 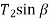
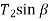
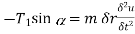
By using (1), we can divide this by
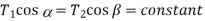

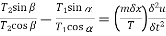
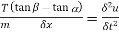
We know that, 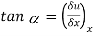 and
and 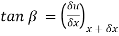


As 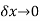
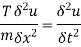
Let 


This is called one-dimensional wave equation.
Solution of Wave Equation by method of separation of variable:
The vibration of an elastic string are governed by are dimensional wave equation
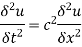
where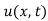 is the deflection of the sting.
is the deflection of the sting.
Since the string is fixed at the ends 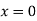 and
and 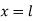 .
.
We have two boundary conditions,
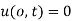 and
and 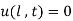 for all t
for all t
We have two initial conditions:

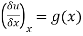
1. If 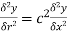 represents the vibrations of a string of length
represents the vibrations of a string of length  fixed at both ends. Find the solution with boundary conditions.
fixed at both ends. Find the solution with boundary conditions.
 and initial conditions.
and initial conditions.

Solution:
Given 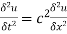
The most general solutions is given by
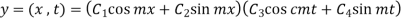
Applying conditions (1), 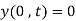
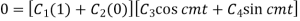

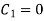
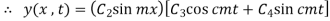
To apply conditions (iii) 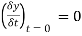 we first obtain
we first obtain 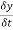
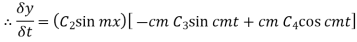
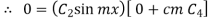
Here, 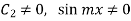
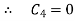
The most general solution will be
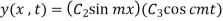

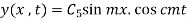 (1)
(1)
Applying condition (ii) 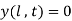
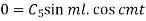
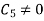 and
and 
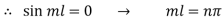

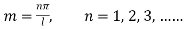
Solution (1) becomes
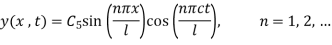
Combining all these solution we get
Applying condition (iv)
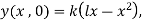
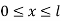
This is Fourier Half Range she series
For
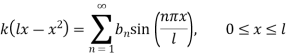
This is Fourier Half Range she series
For 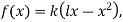
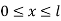
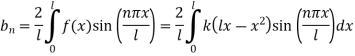


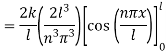

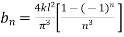
Substituting in equation (2) we get
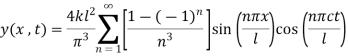
2. A tightly stretched string with fixed end points 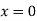 and
and 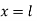 is initially in a position given by
is initially in a position given by  If it is released from rest from this positon. Find the displacement y at any distance x from one end at any time t.
If it is released from rest from this positon. Find the displacement y at any distance x from one end at any time t.
Solution:
The differential equation satisfied by  is
is 

The initial and boundary conditions are given by
(i) 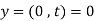
(ii) 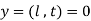
(iii) 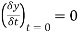
(iv) 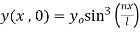
The most general solution is given by
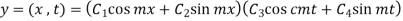
From condition (i) we get, 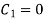
From condition (iii) we get, 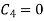
 The most general solution will become
The most general solution will become
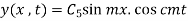 (1)
(1)
From Condition (ii)
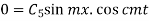

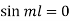

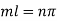
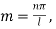
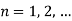
 Equation (1) becomes
Equation (1) becomes
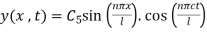
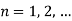
Combining all these solutions we get,
 (2)
(2)
Applying condition (iv)
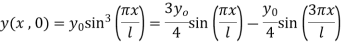
By using 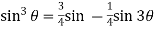


Comparing we get,

Substitute in equation (2) we get,
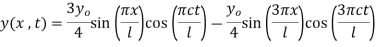
One dimensional Heat flow by method of separation of variables
We have to obtain solution of P.D.E.

The most general solution is
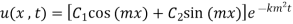
1. Solve: 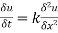 subject to condition
subject to condition
(i) 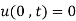
(ii) 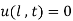
(iii) 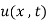 is odd
is odd
(iv) 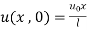 for
for 
Solution:
We have
Step 1: The most general Heat equation is
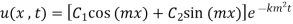 (1)
(1)
Step 2: Use first B.C
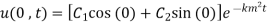
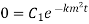
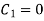
Step 3: Equation (1) becomes
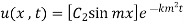 (2)
(2)
Step 4: Use 2nd B.C 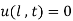
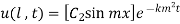
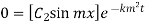

 ,
, 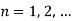
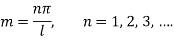
Step 5: Equation (2) becomes
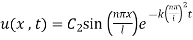
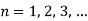
Step 6: Take addition of all solutions and
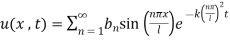 (3)
(3)
Step 7: Use I.C 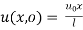
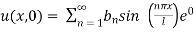
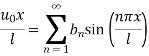
Step 8: To find 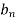 we have,
we have,

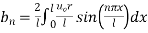
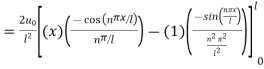
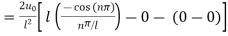
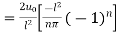
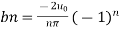
Put in eqn (3) we get,
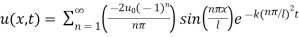
2. Solve :  subject to :
subject to :
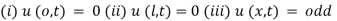
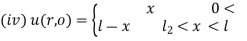
Solution:
We have
Step 1: The most general heart equation is
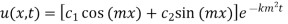 ….. (1)
….. (1)
Step 2: Use B.C 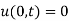
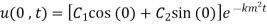
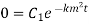
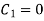
Step 3: Equation (1) becomes
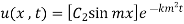 (2)
(2)
Step 4: Use 2nd B.C 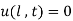
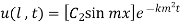
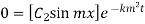
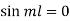
 ,
, 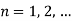
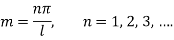
Step 5: Equation (2) becomes
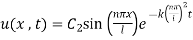
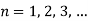
Step 6: Take addition of all solutions and
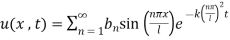 (3)
(3)
Step 7: Use I.C. 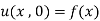

Step 8: To find 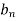
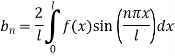
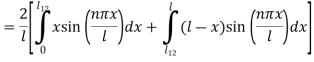
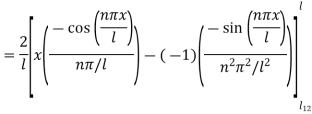
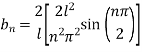
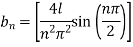
Put in Equation (3) we get,

Two dimensional Heat flow by method of separation of variables:
Two dimensional Heat flow also called Laplace’s equation in two dimensions.
The equation is 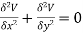
The most general solution is given by

Use this Equation 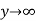 when
when 
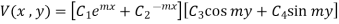
1. Solve the equation 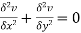 with conditions
with conditions
(i) 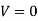 when
when 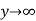 for all
for all 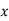 .
.
(ii) 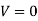 when
when  for all values of
for all values of 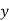 .
.
(iii) 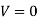 when
when 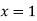 for all values of
for all values of 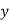 .
.
(iv) 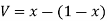 when
when 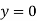 for
for 
Solution:
Here in condition (i), 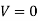 when
when 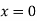 for all values of
for all values of 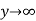 , for all z is given
, for all z is given
Step 1:
The most general solution is
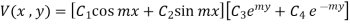 (1)
(1)
Step 2:
Now condition (i) that 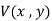 must remain finite as
must remain finite as  , this is possible only if
, this is possible only if 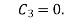
Step 3:
Apply condition (ii) 
Step 4: The equation (1) becomes
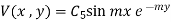
Step 5:
By condition (iii)
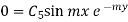
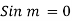

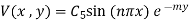

Step 6:
Combining all these solution we get
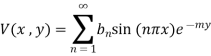
Applying condition (iv) we have
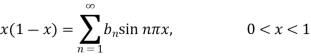
Which is half range since series

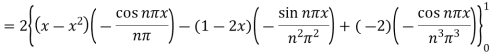
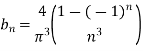
The complete solution is
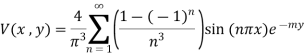
2. A rectangular plate with insulated surfaces is 10 cm wide and so long compared to its width that may be considered infinite in length without introducing an appreciable error. If the temperature along short edge 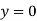 is given
is given 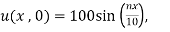
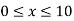 while the two long
while the two long 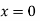 and
and 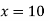 as well as the other short edge are kept at 0
as well as the other short edge are kept at 0 C. Find steady state temperature
C. Find steady state temperature 
Solution:
We have to solve the P.D.E
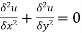
Subject to the conditions
(i) 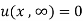
(ii) 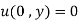
(iii) 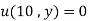
(iv) 
Step 1: The most general solution is
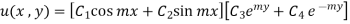 (1)
(1)
Step 2:
By (i) condition, 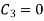
Step 3:
By (ii) condition 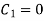
The equation (1) becomes
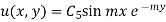
Step 4: By (iii) condition

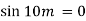
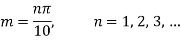

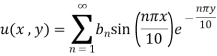
Step 5:
Applying condition (iv), we have
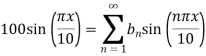
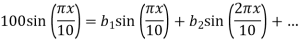
By comparing we get,
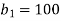 ,
, 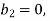
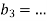
The answer is
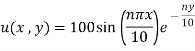
1. Solve by method separation of variables
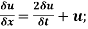 where
where 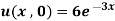
Solution:
Given 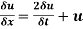
Let the solution of this equation be S
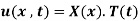
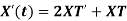
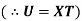
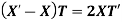
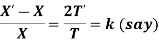
Solving
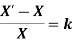
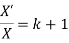
Integrate both sides


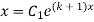
By solving
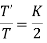
Integrating both sides,
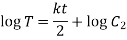
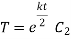
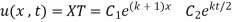
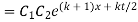
When  ,
,
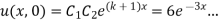 (given)
(given)
By comparing
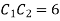
Also
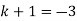
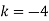
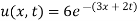
Extra Practice Problems:
1. An infinity long uniform metal plate is enclosed between lines 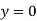 and
and 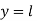 for
for 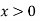 . The temperature is zero along the edges
. The temperature is zero along the edges  and at infinity. If the edge
and at infinity. If the edge 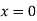 is kept at a constant temperature
is kept at a constant temperature  . Find the temperature distribution
. Find the temperature distribution 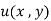 .
.
Solution:
We have to solve P.D.E.
Subject to the boundary condition.
In condition (iii), 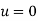 when
when 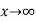 is given
is given
(i) 
(ii) 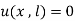
(iii) 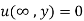
(iv) 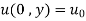
In condition (iii), 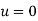 when
when 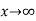 is given
is given
The most general solution is given by
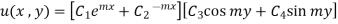
Now condition (iii) u(x , y) must remain as 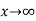
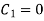
By condition (i) 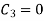

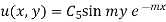
By condition (ii)
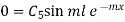
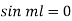
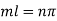
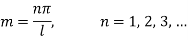
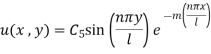
Apply condition (iv) we have
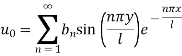
Which is represented by half range Fourier fine series
For 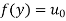 in
in 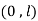
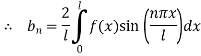
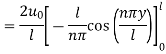
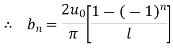
The complete solution is
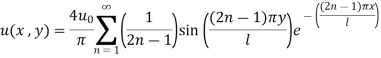
2. Solve the equation where satisfies the following conditions
(i) 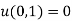
(ii) 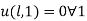
(iii) 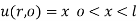
(iv) 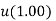 is finite
is finite
Ans:  we have
we have
Solution:
We have
Step 1: The most general solution is
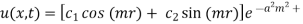
Step 2: Use 1st B.C 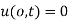

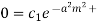

step 3: Equation (1) becomes
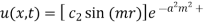
Step 4: Use 2nd B.C 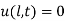


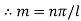 ,
,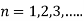
Step 5: Equation (2) becomes
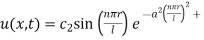
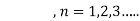
Step 6: Take addition of all solutions and
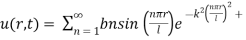
Step 7: Use I.C 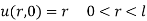
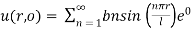
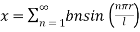
Step 8: To find 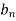 we have
we have
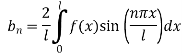
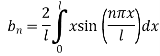

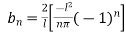
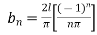
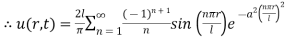
3. A string is stretched and fastened to two points 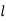 apart. Motion is started by displacing by the string in form from which it is released at time t=0 find the displacement
apart. Motion is started by displacing by the string in form from which it is released at time t=0 find the displacement  from one end.
from one end.
Solution:
We have,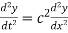
Subject to the condition:
(i) 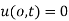
(ii) 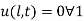
(iii) 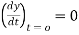
(iv) 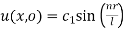
The general solution is
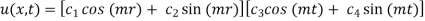
By condition (i) 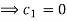
By condition (iii) 
Eq (1) becomes

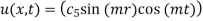
Applying condition (ii) we get
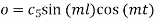
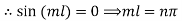
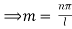
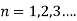
Substituting in equation (2) we get
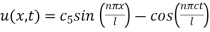
Combining these solutions we get

Applying condition (iv) we get

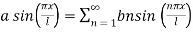
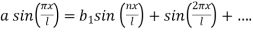
By comparing
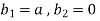
Final Answer is