Unit - 2
Theodolite Surveying
Components of Transit Theodolite (20") and their Function:
A transit theodolite essentially consists of following:
Key Takeaways:
The theodolite in which the telescope can be revolved through a complete revolution about its horizontal axis in a vertical plane is known as transit theodolite.
Procedure:
Elimination or minimization of errors by method of repetition:
Following errors can be eliminated or minimized by this method:
Key Takeaways:
The method in which the angle is measured in clockwise direction for any number of times is known as repetition method.
Procedure:
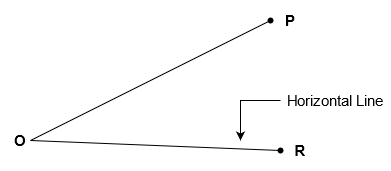
Fig.2.1: Measurement of vertical angle
Key Takeaways:
A vertical angle is the angle between the inclined line of sight and the horizontal line

Fig.2.2: Deflection angle
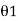
Calculation:
Deflection angle = 180°-included angle
Procedure:
Errors Eliminated:
Following errors are eliminated by this process as the telescope is transited twice.
Key Takeaways:
A deflection angle is the angle which a survey line makes with the prolongation of the proceeding line.
Fig.2.3: Measurement of magnetic bearing
Procedure:
There are three methods of prolonging a straight line by using theodolite.
First method:
Fig.2.4: First method
Second method:
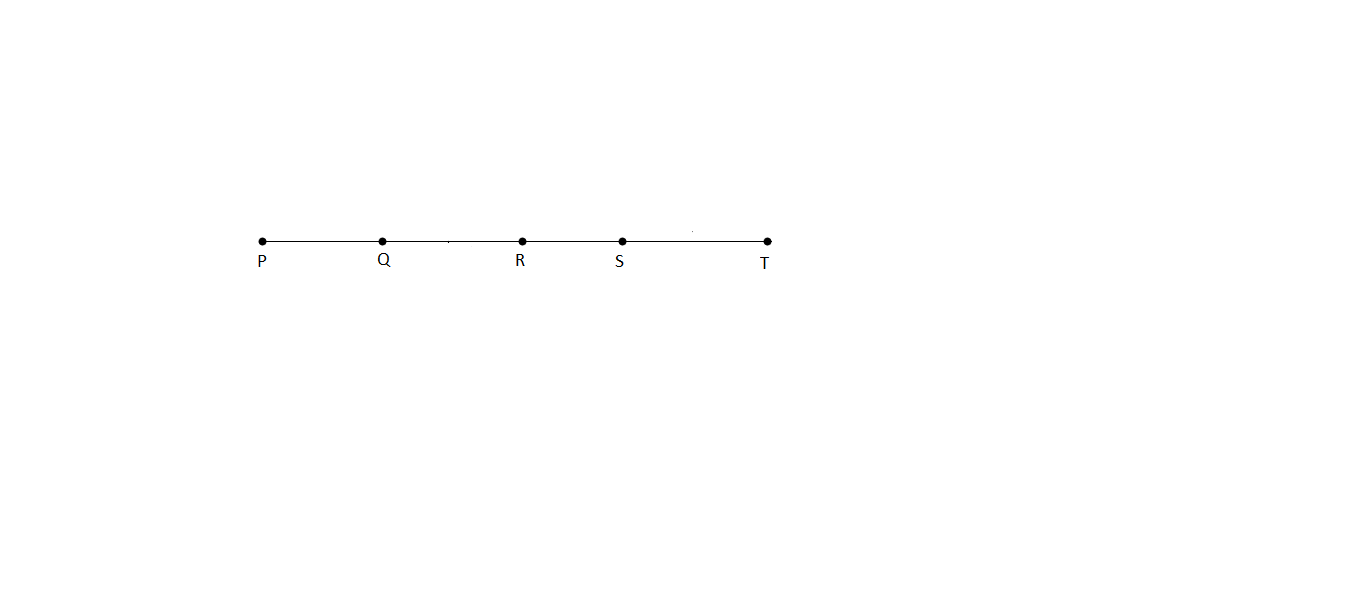
Fig.2.5: Second method
It is required to prolong a line PQ up to the point T.
Third method:
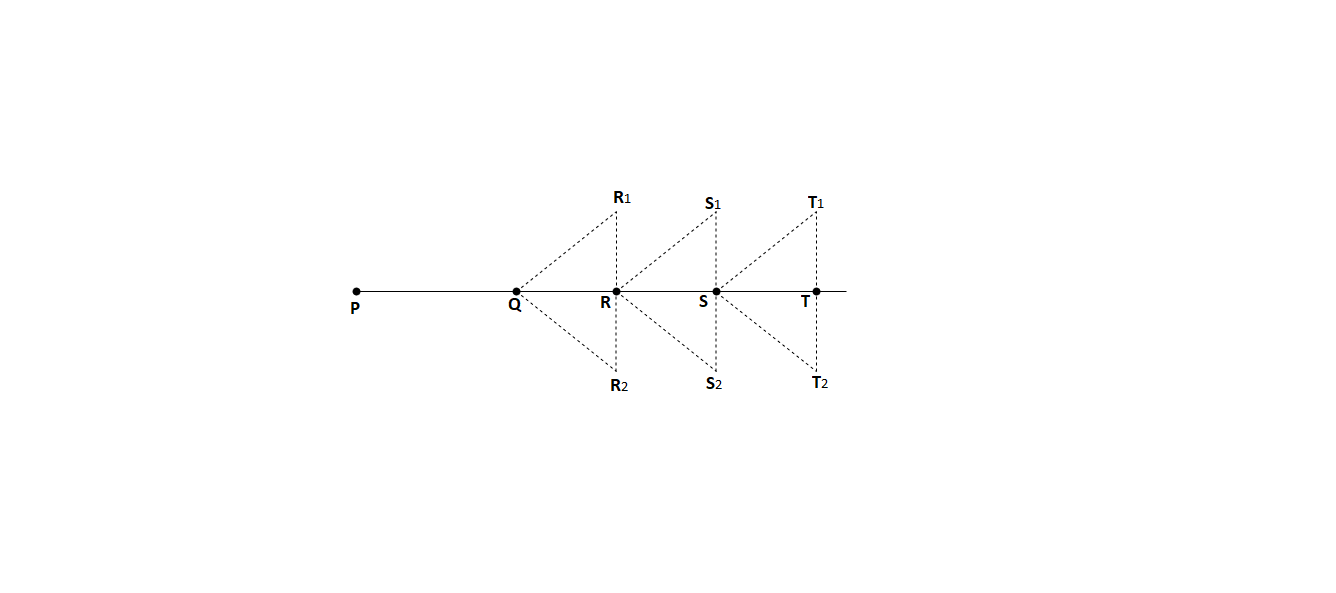
Fig.2.6: Third method
Procedure:
Key Takeaways:
There are three types of methods:
Key Takeaways:
This process could be encouraged wherein it's far assumed that the theodolite needs to be targeted over a nail withinside the pinnacle of a peg. It is a normal factor or reference mark used withinside the creation and placing out.
The Fundamental Axes of the Theodolite are:
Permanent adjustment of theodolite consists of the following:
(1) Adjustment of plate level:
Condition:
To make the axis of plate level perpendicular to the vertical axis.
Necessity:
Test:
Adjustment:
(2) Adjustment of line of collimation:
Condition:
Necessity
(a) Horizontal hair:
(b) Vertical hair:
Testing and adjustment:
(a) Horizontal hair:
Test:
Adjustment:
(b) Vertical hair:
Test:
Adjustment:
(3) Adjustment of horizontal axis:
Condition:
Necessity:
Test:
Adjustment:
(4) Adjustment of the bubble line of the altitude level:
Condition:
Necessity:
Test:
Adjustment:
(5) Adjustment of the vertical index frame:
Condition:
Necessity:
Test:
Adjustment:
Key Takeaways:
Permanent adjustment of theodolite consists of the following:
Key Takeaways:
The technique of repetition used to degree traverse angles to a finer diploma of accuracy than that workable with the least be counted number of the vernier geared up at the theodolite.
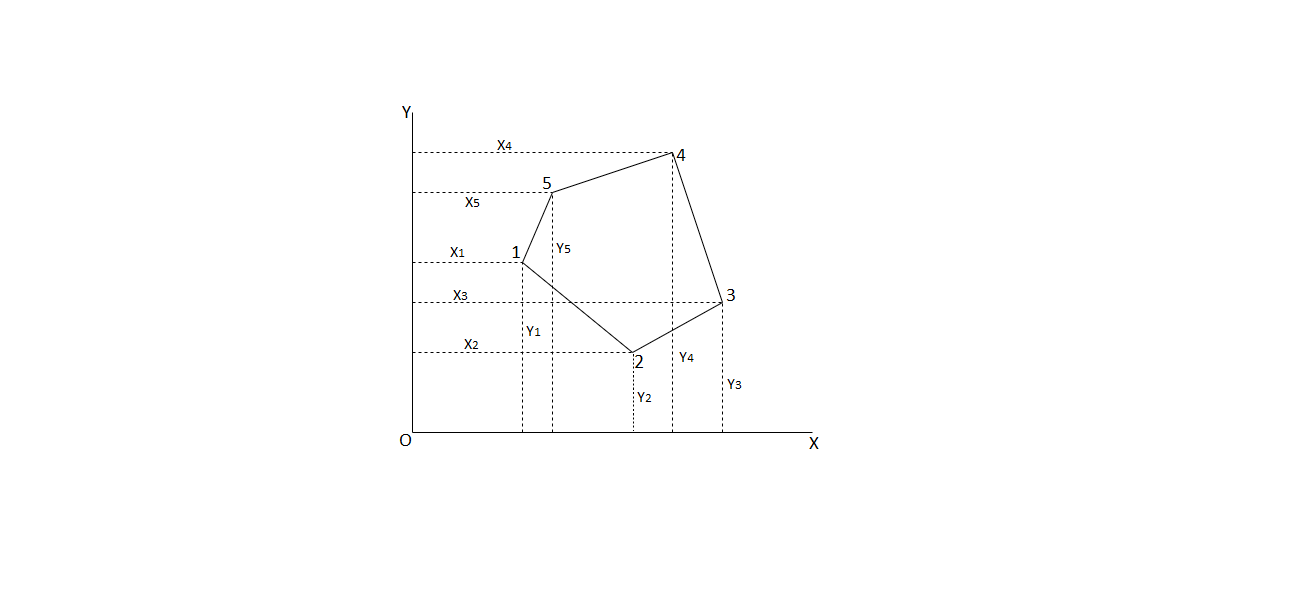
Fig.2.7: Traverse computation
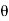
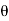 = the reduced bearing of the line,
= the reduced bearing of the line,
l= the length of line.
Consecutive Co-ordinates:
Independent Co-ordinates: (Total Latitude and Total Departure)
Key Takeaways:
Consecutive Co-ordinates: The latitude and departure of any point with reference to the preceeding point are called consecutive co-ordinates of the point.
Independent Co-ordinates: The co-ordinates of any point with respect to a common origin are called as independent co-ordinates of the point.
The transit rule may be employed to balance the traverse when the angular measurements are more precise than the linear measurement.
Correction to latitude of any side= Total error in latitude×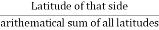
Correction to departure of any side=
Total error in departure x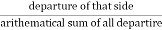
Total error in latitude or departure×
The calculations for a closed traverse may be made in the following steps and entered in a tabular form which is known as Gale's Traverse Table:
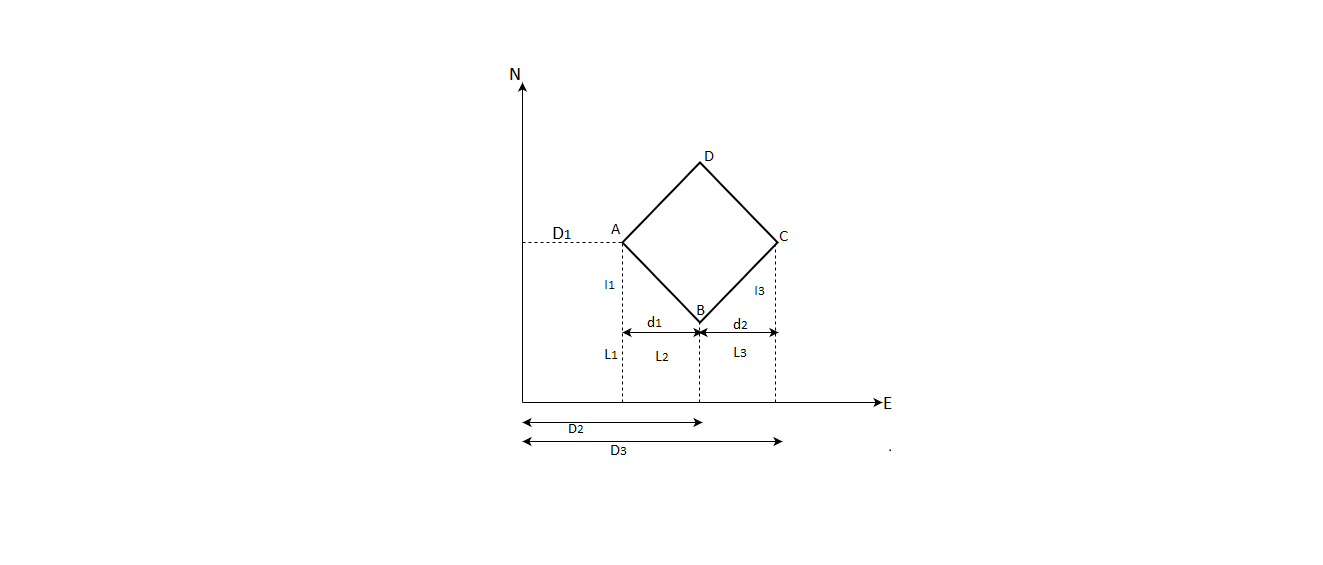
Fig.2.8: Area calculation
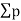 = (y1x2+y2x3+y3x4+y4x5+y5x1)
= (y1x2+y2x3+y3x4+y4x5+y5x1)
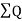 = (x1y2+x2y3+x3y4+x4y5+x5y1)
= (x1y2+x2y3+x3y4+x4y5+x5y1)
Double area=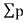 -
-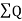
∴Required area= 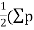 -
-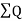 )
)
Key Takeaways:
The given consecutive coordinates of a traverse are converted into independent co-ordinates with reference to the co-ordinates of the most westernly, thus the whole traverse is transferred to the 1st quadrant.
References: