Unit - 4
Curves
Horizontal curve:
Vertical Curve:
Key Takeaways:
The curves which are provided at turning points so as to get gradual change in the direction of alignment of a road or a track are termed as horizontal curves.
The curves which are provided in the alignment of road or track at change of gradient is termed as vertical curves.
There are four types of horizontal curves:
Simple curve:

Fig.4.1: Simple curve
Compound curves:
for better understanding.
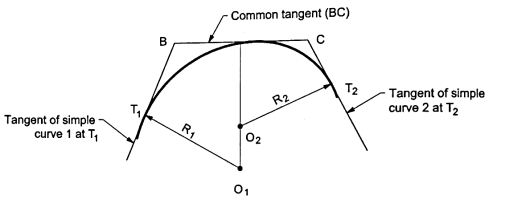
Fig.4.2: Compound curve
Reverse curve:
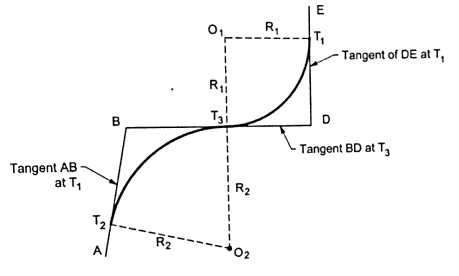
Fig.4.3: Reverse curve
Advantages of reverse curve:
Disadvantages of reverse curve:
Transition curve:
There are Two types of vertical curve:
Summit curves:
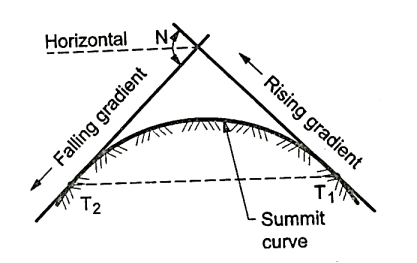
Fig.4.4: A rising gradient intersecting a falling gradient

Fig.4.5: A rising gradient meeting another rising gradient
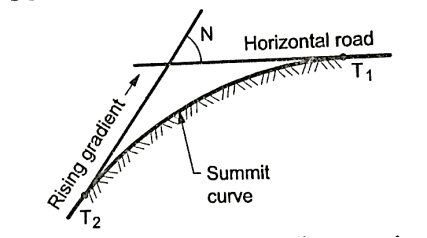
Fig.4.6: A rising gradient meeting at horizontal road
Valley curves:
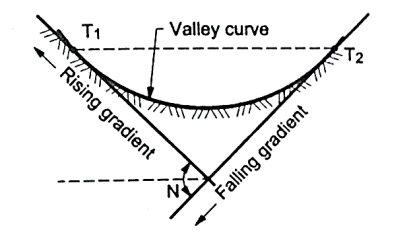
Fig.4.7: A falling gradient intersecting a rising gradient

Fig.4.8: A falling gradient meeting another falling gradient
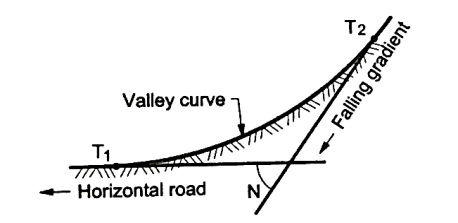
Fig.4.9: A falling gradient meeting a horizontal road
Key Takeaways:
There are four types of horizontal curves:
There are Two types of vertical curve:

Fig.4.10: Simple circular curve (Right hand curve)
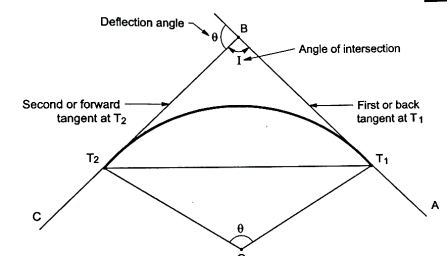
Fig.4.11: Simple circular curve (left hand curve)
4. In Fig., the curve deflects to left side. Therefore, it is called as left-hand curve.
5. In Fig., BC is first tangent and also called as back tangent. AB is second tangent and also called as forward tangent. In Fig. AB is first or back tangent at T₁ and BC is second or forward tangent at T₁.
6. T1, and T2, are the tangent points. T1, shows the starting of the curve and T2, shows the end of the curve.
7. In fig., I is an angle of intersection and 0 is a deflection angle.
8. BT1, and B T2, are the lengths of tangent.
9. T1, T2, is a long chord of length 'L'.
10. The arc 'T1ET2' is a length of curve.
11. The midpoint 'E' is apex of summit of the curve T1ET2
12. BE is the distance of apex.
13. The angle 'T1OT2' = The deflection angle ' '.
'.
14. DE is a versed sine of the curves.
Key Takeaways:
Elements of the Simple of the Curve:
Refer the Fig. to obtain the various elements of the simple circular curve.



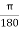
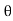
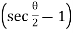

Fig.4.12: Compound curve
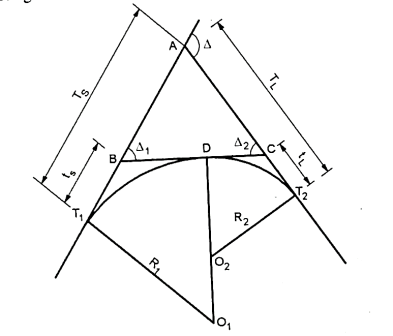
Fig.4.13: Two centered compound curve
Let,
Rs =the smaller radius (T1O1)
R2= the longer radius (T2O2)
BC= common tangent
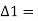 deflection angle between the rear and the common tangent.
deflection angle between the rear and the common tangent.
 =deflection angle between the common and the forward tangent.
=deflection angle between the common and the forward tangent.
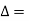 total deflection angle.
total deflection angle.
ts=the length of the tangent to the arc (T, D) having a smaller radius.
Ts = tangent distance T1A corresponding to the shorter radius.
TL = tangent distance T2A corresponding to the longer radius.
From Fig. we have,
ts= T1B= BD= Rs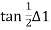
tl=T2C=CD+RL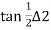
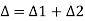
From triangle ABC we have,
Ts=T1B+BA
=ts+(ts+tl)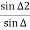
Key Takeaways:
A curve of having the series of two and more simple curves of different radii curving in the same direction is called as compound curves.
Radial offsets:
T1P = x
From Δ T1 PO,
PO2 = T1O2+T1 P²
Ox=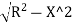 –R …... (1)
–R …... (1)
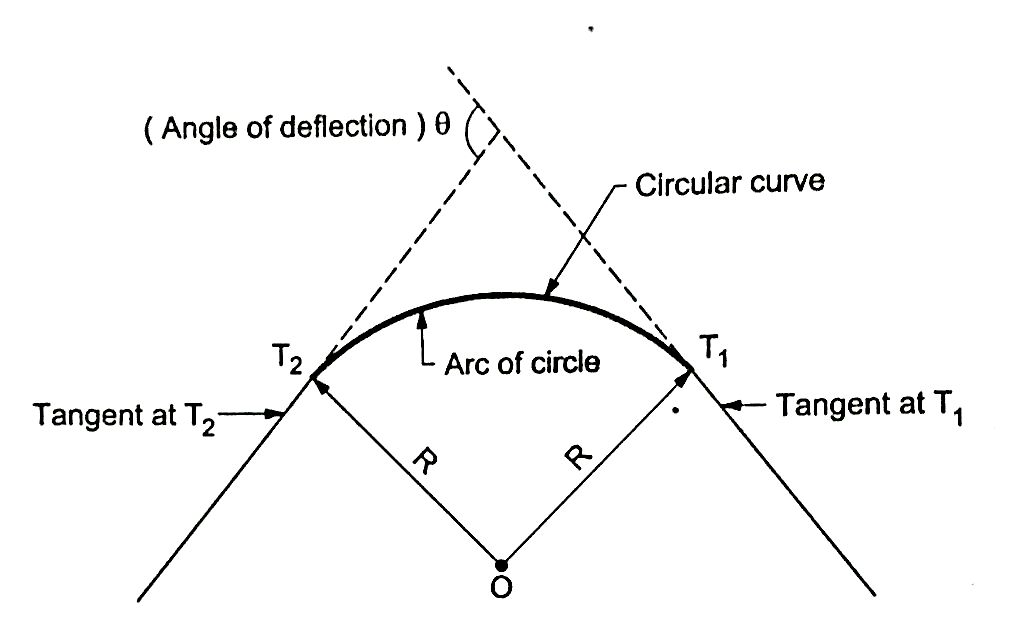
Fig.4.14: setting out by radial offsets
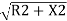
Thus,
Ox=R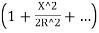 -R
-R
Neglecting the other terms except the first two, we get
Or Ox=x2/ 2R
When the radius is large
T1P2=PN(2R+PN)
X2=Ox(2R+Ox)
Neglecting Ox in comparison to 2R we get
Ox=x2/2R
Perpendicular offsets:
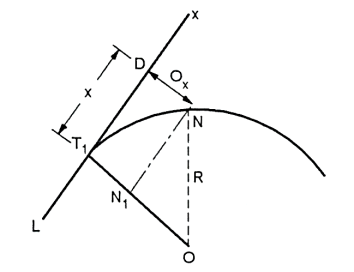
Fig.4.15: setting out by perpendicular offsets
T1D=x= measured along the tangent
Draw NN1 parallel to the tangent
From  leEE1O, we have
leEE1O, we have
E1O2=EO2-E1E2
(R-Ox)2=R2-x2
From which
Ox=R-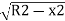
The corresponding approximate expression for Ox may be obtained by expanding the term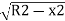 . Thus,
. Thus,
Ox=R-R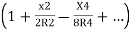
Neglecting the other terms except the first two of the expressions
Ox=R-R+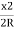
Offset from long chord is calculated as:
L=2R 
Where R =Radius of curve
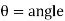
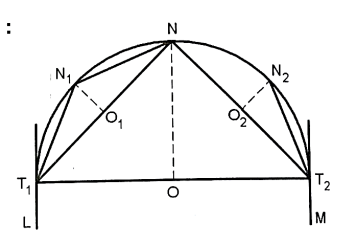
Fig.4.16: Successive bisection of arcs
NO= R (1-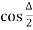 )
)
=R-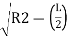 ^2
^2
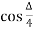
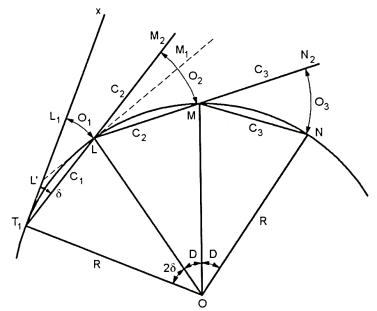
Fig.4.17: setting out the curve by deflection distance
Let T1L1 = T1L = initial sub-cord= C1
L, M, W are the points on curve
LM = C2, MN = C3 etc
T1x = rear tangent
∠ L1 T1 L =  = deflection angle of the first chord
= deflection angle of the first chord
L1 L =O1 = first offset
M2 M = O2 = second offset
N2 N = O3 = Third offset etc.
Now Arc L1 L = O1 = T1 L 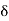 ……(1)
……(1)
Since T1x is the tangent to the circle at T₁
∠T O L = 2∠L T L
= 2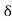
∴ T L = R 2 
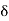 =
= 
Substituting the value of 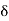 in (1) we get
in (1) we get
Arc L1 L = O1 = T1L 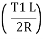
 = T1 L2
= T1 L2
2R
Taking arc T1L=chord T1L (very nearly) we get
O1=C1^2/2R
The O2= M2M
As from equation No. 3, the offsets M1M from the tangent LM1 is given by
L1L =C22 /2R
Angle M2LM1=angle L’LT1 being opposite angles
Again,
Since T1L' and L'L are both tangents, they are equal in length.
Arc M2M1=LM2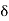 =C2
=C2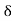
O12=C2/2R
O₂ = C/2R(C+C)
03= 04=C/2R(2C)
=C2/R
Angular methods which are most commonly used for setting out a circular curve are:
Derivation of formula:
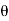
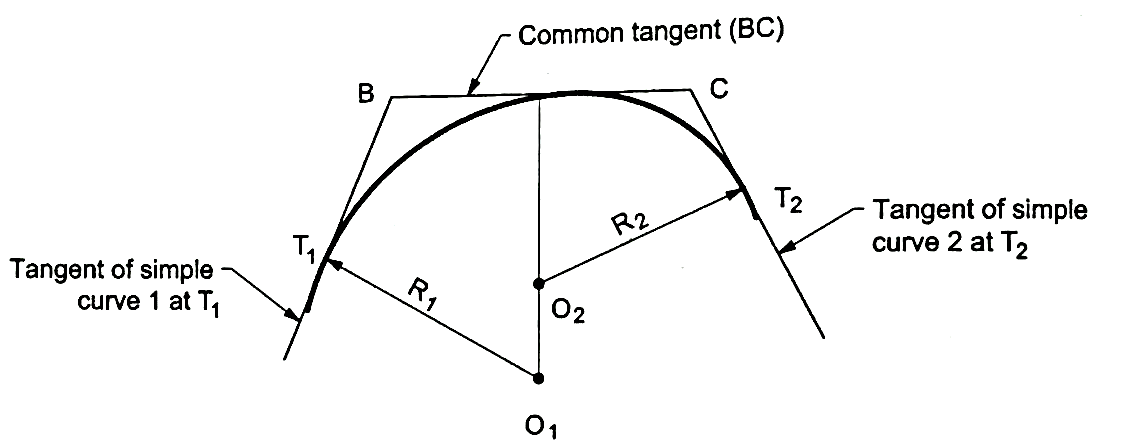
Fig.4.18: Rankine’s method of tangential angle or deflection angle
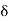
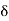
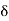
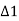
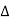
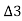
BT1E = 8, = ½ T1OE
T1OE = 2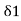 ,
,
Now,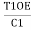 =
=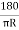
T1OE = C1
C1
2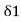 =
=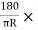 C1
C1
 minutes
minutes
Similarly, 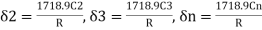
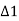
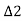
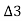
∴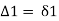
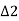
Hence,
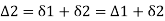

Stepwise procedure for setting the curve by deflection angles:
Peg or point | Chainage in m | Chord length in m | Deflection angle | Total deflection angle | Actual theodolite reading | Offset in m | Remark |
|
|
|
|
|
|
|
|
Key Takeaways:
Transit theodolite and chain or tape are used in this method. Since this method gives more precise results, it is mostly used for setting out the curves in railways and other important work.
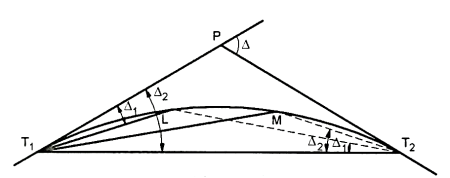
Fig.4.19: Two theodolite method
Thus, in Fig.
<PT1L= A=Deflection angle for L.
But LT2T1, is the angle subtended by the chord T, L in the opposite segment.
∴ angle LT2T1= angle PT1M =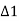
Similarly, angle PT1L=  = angle T1T2M
= angle T1T2M
Hence the angle between the long chord and the line joining any point to T2 is equal to the deflection angle to the point measured with respect to the rear tangent.
Method of setting out the Curve:
Advantage of two theodolite method:
Disadvantage of two theodolite method:
Key Takeaways:
This method is based on the principle that "The angle between the tangent and the chord is equal to the angle which that chord subtends in the opposite segment.
Two straights intersect at a chainage of 2610 m, the deflection angle being 36 A circular curve of 400 m radius is to be set. Calculate the chainages of the tangent point of right-handed circular curve. Peg interval is 30 m.
Given: Deflection angle (0) = 36°.
BT₁ Tangent length = R tan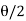 =400
=400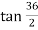 129.967 =129.97 m
129.967 =129.97 m
= (4+9.97) chains
Length of curve =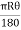 =
=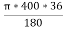 =251.327=251.33m
=251.327=251.33m
= (8+11.33) chains
Chainage of the second tangent point "T1':
=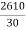 -(4+9.97) chains
-(4+9.97) chains
= (87) -(4+9.97) chains
= (83+9.97) chains
Chainage of the second tangent point ‘T2':
= (Chainage of T,) + (length of curve)
= (83 +9.97) + (8 +11.33)
= (91 +21.3) chains
Two roads meet at an angle of 150. Calculate the data necessary for setting out curve of 10 chains radius to connect the two straight roads if it intended to set out curve by chain and offset from long chord, chain used is a 30 m chain only. Calculate two offsets from centre of long chord.
Given:
I =point of intersection
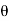 =deflection angle = 180° - 150° = 30°
=deflection angle = 180° - 150° = 30°
R = radius of curve = 10 chains = 10x30=300 m (since 30 m chain used)
Length of long chord (L) =2 R sin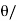 2
2
L = 2x300 x sin 30°/2 = 155.29 m
Note: Length of long chord is taken in round figures as 160 m.
∴L = 160 m
Ordinate at the middle of the long chord (O)= versed sine
O0 = R-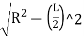
=300-
O0=300-289.136
∴O0=10.86 m
The various ordinates can be calculated by the following formula as,
Ox=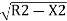 –(R-O0)
–(R-O0)
Consider the offset at 20 m from the centre.
O20=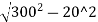 -(300-10.86)
-(300-10.86)
=299.33-289.14=10.19 m
(It is the first offset from the centre of long chord)
O40=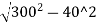 -(300-10.86)
-(300-10.86)
=297.32-289.14=8.18m
(It is the second offset from the centre of long chord.)
Hence the two offsets from the center of long chord are 10.19 m and 8.18 m.
Extension of problem:
Remaining offsets till curve ends can be calculated as follows:
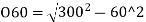 -(300-10.86)
-(300-10.86)
=293.938-289.14
=4.8 m
O80=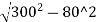 -(300-10.86)
-(300-10.86)
=289.136-289.14
=0 m
Necessity:
Key Takeaways:
The curve in which radius varies gradually from infinity to a finite value equal to that of the circular curve to be connected and vice versa is termed as transition curve.
References: