1.1 Logic Design Minimization Technique Minimization of the Boolean function using Kmap up to 4 variables and Quine McClusky Method

DELD

Unit I

Minimization Technique

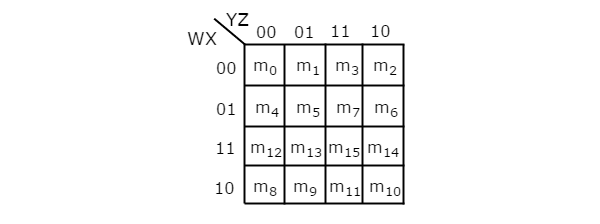
1.1 Logic Design Minimization Technique: Minimization of the Boolean function using K-map (up to 4 variables) and Quine Mc-Clusky Method

1) Variable K-Map

It has 16 numbers of cells since the number of variables is 4.

The 4 variable K-Map is:

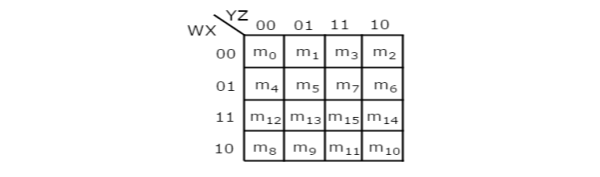
Fig. : 4 variable K-Map

The only way to group 8 adjacent min terms.

Let R1, R2, R3, and R4 represent the min terms of the first row, second row, third row, and fourth row respectively.

Similarly, C1, C2, C3, and C4 represent the min terms of the first column, second column, third column, and fourth column respectively.

The possible combinations are {(R1, R2), (R2, R3), (R3, R4), (R4, R1), (C1, C2), (C2, C3), (C3, C4), (C4, C1)}.

If w=0, then 4 variable K-map becomes 3 variable K-map.

Rules for simplifying K-maps:

Selecting K-map based on the number of variables present in the Boolean function.

If the Boolean function is in Max terms form, then place the zeroes at respective Max term cells in the K-map.

If the Boolean function is in PoS form, then place the zeroes wherever required in K-map for which the given sum terms are valid.

The maximum possibilities of grouping are checked for adjacent zeroes.

It should be of powers of two.

Starting from the highest power of two and to the least power of two.

The highest power is equivalent to the number of variables considered in K-map and the least power is zero.

Each group will give either a literal or one sum term.

It is known as prime implicant.

The prime implicant is an essential prime implicant when at least a single ‘0’ is not covered with any other groups but only that grouping covers.

The simplified Boolean function contains all essential prime implicants and only the required prime implicants.

Numericals

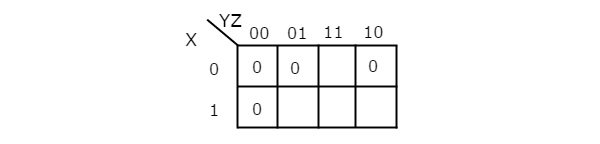
Simplify f(X,Y,Z)=∏M(0,1,2,4)f(X,Y,Z)=∏M(0,1,2,4)using K-map.

Prime Implicants

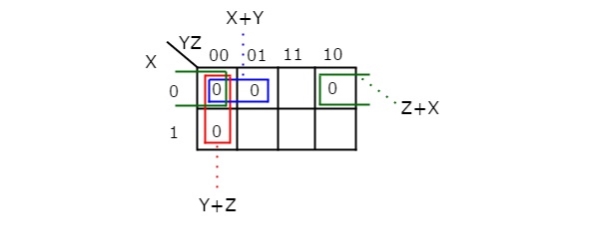
ungrouped

Therefore, the simplified Boolean function is

f = (X + Y).(Y + Z).(Z + X)

Simplify:

F(P,Q,R,S)=∑(0,2,5,7,8,10,13,15)

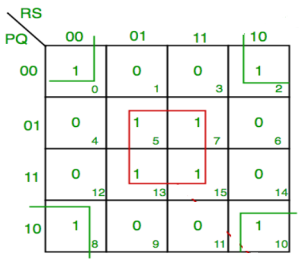
F = P’Q’R’S’ + PQ’R’S’ + P’Q’RS’ +PQ’RS’ + QS

F = P’Q’S’ + PQ’S’ + QS

F = Q’S’ +QS

Simplify:

F(A,B,C)=π(0,3,6,7)

F = A’BC +ABC +A’B’C’ +ABC’

F = BC + C’ ( A’B’ + AB )

2) Quine-McCluskey Tabular Method

K-map method is a convenient method for the minimization of Boolean functions up to 5 variables. But, it is very difficult to simplify more than 5 variables by using this method.

Quine-McCluskey is a tabular method based on the concept of prime implicants.

Prime implicant is a product (or sum) term, which cannot be further reduced by combining with any other product (or sum) terms in the given Boolean function.

This tabular method gets the prime implicants by repeatedly using the following Boolean identity.

xy + xy’ = x(y + y’) = x.1 = x

The procedure of Quine-McCluskey Tabular Method

Steps for simplifying Boolean functions using the Quine-McCluskey method:

Step 1 − Arranging the given min terms in ascending order and making groups based on the number of one’s presence in the binary representations.

So, there are at most ‘n+1’ groups if there are ‘n’ Boolean variables or ‘n’ bits in the binary equivalent of min terms.

Step 2 − Comparing the min terms present in successive groups. If there is a change in only a one-bit position, then taking the pair of two min terms. Placing the symbol ‘_’ in the differed bit position and keeping the remaining bits as it is.

Step 3 − Repeating step2 with newly formed terms until we get all required prime implicants.

Step 4 − Formulating the prime implicant table which consists of a set of rows and columns. It can be placed row-wise and min terms can be placed column-wise. Put ‘1’ in the cells corresponding to the min terms that are covered in each prime implicant.

Step 5 – Now find the essential prime implicants by observing each column. If the minterm is covered by one prime implicant, then it is called as essential prime implicant. They will be a part of the simplified Boolean function.

Step 6 – The prime implicant table is reduced by removing the row and columns of each essential prime implicant corresponding to the min terms. This process is stopped when all min terms of given Boolean function are over.

Example

Simplify, f(W,X,Y,Z)=∑m(2,6,8,9,10,11,14,15) and f(W,X,Y,Z)=∑m(2,6,8,9,10,11,14,15)

using Quine-McClukey tabular method.

Solution:

Group Name	Min terms	W	X	Y	Z
GA1	2	0	0	1	0
GA1	8	1	0	0	0
GA2	6	0	1	1	0
	9	1	0	0	1
	10	1	0	1	0
GA3	11	1	0	1	1
GA3	14	1	1	1	0
GA4	15	1	1	1	1

Group Name	Min terms	W	X	Y	Z
GB1	2,6	0	-	1	0
	2,10	-	0	1	0
	8,9	1	0	0	-
	8,10	1	0	-	0
GB2	6,14	-	1	1	0
	9,11	1	0	-	1
	10,11	1	0	1	-
	10,14	1	-	1	0
GB3	11,15	1	-	1	1
GB3	14,15	1	1	1	-

Group Name	Min terms	W	X	Y	Z
GB1	2,6,10,14	-	-	1	0
	2,10,6,14	-	-	1	0
	8,9,10,11	1	0	-	-
	8,10,9,11	1	0	-	-
GB2	10,11,14,15	1	-	1	-
GB2	10,14,11,15	1	-	1	-

Group Name	Min terms	W	X	Y	Z
GC1	2,6,10,14	-	-	1	0
	8,9,10,11	1	0	-	-
GC2	10,11,14,15	1	-	1	-

Therefore, the prime implicants are YZ’, WX’ & WY.

The prime implicant table is shown below.

Min terms / Prime Implicants	2	6	8	9	10	11	14	15
YZ’	1	1			1		1
WX’			1	1	1	1
WY					1	1	1	1

The reduced prime implicant table is shown below.

Min terms / Prime Implicants	8	9	11	15
WX’	1	1	1
WY			1	1

Min terms / Prime Implicants	15
WY	1

Hence, f(W,X,Y,Z) = YZ’ + WX’ + WY.

Simplify ( ref: internet)

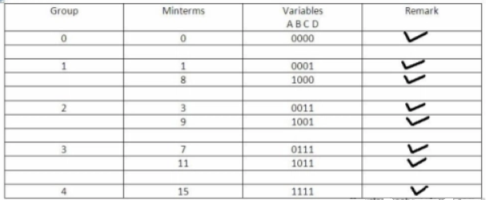
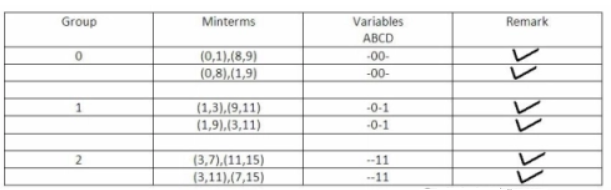
Y(A,B,C,D) =∑ m(0,1,3,7,8,9,11,15)

Groups are made with respect to the no. of one’s present.

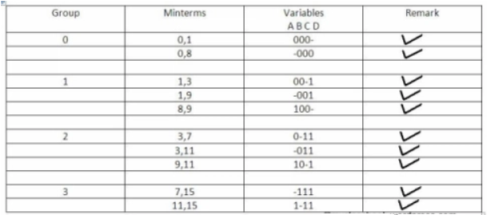
Now, comparing with the above table wherever we have a different bit present we put a ’-‘ there.

The same thing is done by comparing it from the above table.

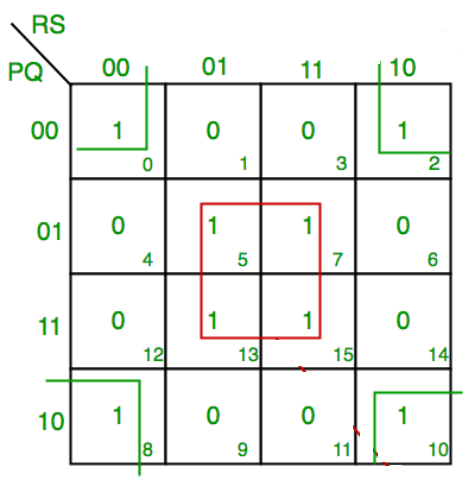
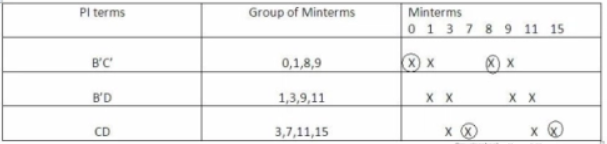
The table for prime implicants is:

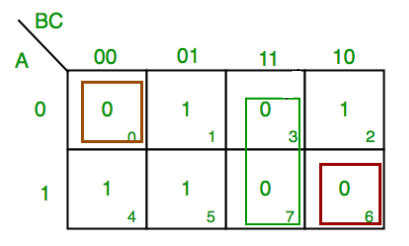
Rounding the min terms which has X in the column and hence the final answer is B’C’ + CD.

1.2 Representation of signed number- sign-magnitude representation

Convert the following decimal values into signed binary numbers using the sign-magnitude format:

-1510 as a 6-bit number	⇒	1011112
+2310 as a 6-bit number	⇒	0101112
-5610 as a 8-bit number	⇒	101110002
+8510 as a 8-bit number	⇒	010101012
-12710 as a 8-bit number	⇒	111111112

Note that for a 4-bit, 6-bit, 8-bit, 16-bit or 32-bit signed binary number all the bits MUST have a value, therefore “0’s” are used to fill the spaces between the leftmost sign bit and the first or highest value “1”.

The sign-magnitude representation of a binary number is a simple method to use and understand for representing signed binary numbers, as we use this system all the time with normal decimal (base 10) numbers in mathematics. Adding a “1” to the front of it if the binary number is negative and a “0” if it is positive.

However, using this sign-magnitude method can result in the possibility of two different bit patterns having the same binary value.

1.3 1’s complement and 2’s complement form (red marked can be removed)

1's complement

Here, a number is obtained by changing all 1's to 0's and all 0's to 1's.

This is called as 1's complement.

For Example :

1's complement

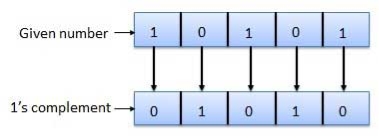
Fig.: 1's complement

2's complement

It is obtained by adding 1 to the Least Significant Bit (LSB) of 1's complement of the number.

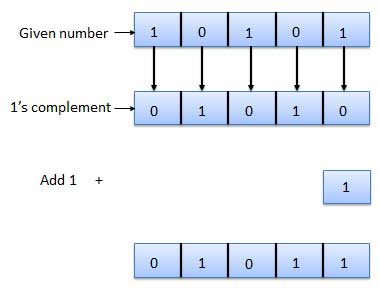Hence, 2's complement = 1's complement + 1

For Example:

Fig.: 2's complement

1.4 Sum of product and Product of sum form

Four product combinations is obtained by combining two variables x and y with logical AND operation. They are called as min terms or standard product terms. The min terms are given as x’y’, x’y, xy’ and xy.

In the same way, four Boolean sum terms is obtained by combining two variables x and y with logical OR operation. They are called as Max terms or standard sum terms. The Max terms are given as x + y, x + y’, x’ + y and x’ + y’.

The following table represents the min terms and MAX terms for 2 variables.

x	y	Min terms	Max terms
0	0	m0=x’y’	M0=x + y
0	1	m1=x’y	M1=x + y’
1	0	m2=xy’	M2=x’ + y
1	1	m3=xy	M3=x’ + y’

If the binary variable is ‘0’, then it is represented as complement of variable in min term and as the variable itself in Max term.

Similarly, if it is ‘1’, then it is represented as complement of variable in Max term and as the variable itself in min term.

From the above table, we can easily notice that min terms and Max terms are complement of each other.

If there are ‘n’ Boolean variables, then there will be 2n min terms and 2n Max terms.

Canonical SoP and PoS forms

A truth table comprises of a set of inputs and output(s).

If there are ‘n’ input variables, then there shall be 2n possible combinations comprising of zeros and ones.

So the value of every output variable depends on the combination of input variables.

Hence, each output variable have ‘1’ for some combination and ‘0’ for other combination of input variables.

Therefore, we can express each output variable in two ways.

Canonical SoP form

Canonical PoS form

Canonical SoP form

It means Canonical Sum of Products form.

In this, each product term contains all literals.

So that these product terms are nothing but the min terms.

Hence is also known as sum of min terms form.

Firstly, identification of the min terms is done and then the logical OR of those min terms is taken in order to get the Boolean expression (function) corresponding to that output variable.

This Boolean function will be in sum of min terms form.

Then following the same procedure for other output variables too.

Example

Considering the following truth table.

Inputs		Output
P	q	r	f
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

Here, the output (f) is ‘1’ for only four combinations of inputs.

The corresponding min terms are given as p’qr, pq’r, pqr’, pqr.

By doing logical OR, we get the Boolean function of output (f).

Hence, the Boolean function of output is,

f = p’qr + pq’r + pqr’ + pqr.

This is the desired canonical SoP form of output, f.

It can also be represented as:

f=m3+m5+m6+m7f=m3+m5+m6+m7

f=∑m(3,5,6,7)f=∑m(3,5,6,7)

First, we represented the function as sum of respective min terms and then, the symbol for summation of those min terms is used.

Canonical PoS form

It means Canonical Product of Sums form.

Here In this form, each sum term contains all literals.

These sum terms are the Max terms.

Hence, canonical PoS form is also known as product of Max terms form.

Identification of the Max terms for which the output variable is zero is done and then the logical AND of those Max terms is done in order to get the Boolean expression corresponding to that output variable.

This Boolean function is in the form of product of Max terms.

Following the same procedure for other output variables too.

Standard SoP and PoS forms

Standard SoP form

It stands for Standard Sum of Products form.

In this, each product term need not contain all literals.

So, the product terms can or cannot be the min terms.

Therefore, it is therefore the simplified form of canonical SoP form.

Standard SoP of output variable can be obtained by two steps.

Getting the canonical SoP form of output variable

Simplification the above Boolean function.

The same procedure is followed for other output variables too, if there is more than one output variable.

Numerical

Convert the Boolean function into Standard SoP form.

f = p’qr + pq’r + pqr’ + pqr

Solution:

Step 1 – By using the Boolean postulate, x + x = x and also writing the last term pqr two more times we get

⇒ f = p’qr + pq’r + pqr’ + pqr + pqr + pqr

Step 2 – By Using Distributive law for 1st and 4th terms, 2nd and 5th terms, 3rdand 6th terms.

⇒ f = qr(p’ + p) + pr(q’ + q) + pq(r’ + r)

Step 3 – Then Using Boolean postulate, x + x’ = 1 we get

⇒ f = qr(1) + pr(1) + pq(1)

Step 4 – hence using Boolean postulate, x.1 = x we get

⇒ f = qr + pr + pq

⇒ f = pq + qr + pr

This is the required Boolean function.

Standard PoS form

It stands for Standard Product of Sum form.

Here, each sum term need not contain all literals.

So, the sum terms can or cannot be the Max terms.

Therefore, it is the desired simplified form of canonical PoS form.

Standard PoS form of output variable is obtained by two steps.

Getting the canonical PoS form of output variable

Simplification of the above Boolean function.

The same procedure is followed for other output variables too.

Numerical

Convert the Boolean function into Standard PoS form.

f = (p + q + r).(p + q + r’).(p + q’ + r).(p’ + q + r)

Solution:

Step 1 – By using the Boolean postulate, x.x = x and writing the first term p+q+r two more times we get

⇒ f = (p + q + r).(p + q + r).(p + q + r).(p + q + r’).(p +q’ + r).(p’ + q + r)

Step 2 – Now by using Distributive law, x + (y.z) = (x + y).(x + z) for 1st and 4thparenthesis, 2nd and 5th parenthesis, 3rd and 6th parenthesis.

⇒ f = (p + q + rr’).(p + r + qq’).(q + r + pp’)

Step 3 − Applying Boolean postulate, x.x’=0 for simplifying of the terms present in each parenthesis.

⇒ f = (p + q + 0).(p + r + 0).(q + r + 0)

Step 4 − Using Boolean postulate, x + 0 = x we get

⇒ f = (p + q).(p + r).(q + r)

⇒ f = (p + q).(q + r).(p + r)

This is the simplified Boolean function.

Hence, both Standard SoP and Standard PoS forms are Dual to one another.

1.5 Minimization of SOP and POS using K-map

Karnaugh introduced a method for simplification of Boolean functions in an very easy way.

This method is known as Karnaugh map method or K-map method.

It is a graphical method, which comprises of 2n cells for ‘n’ variables.

Here, the adjacent cells varies only in single bit position.

K-Maps for 2 to 5 Variables

It is the most suitable method for minimizing Boolean functions of 2 variables to 5 variables.

2 Variable K-Map

It has 4 number of cells since the number of variables is two.

The 2 variable K-Mapis :

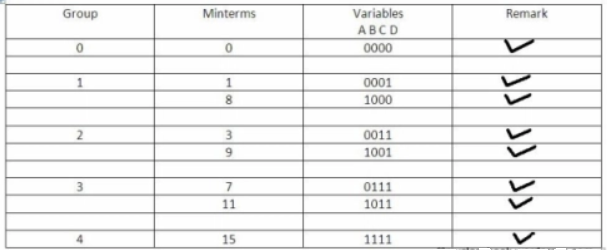
Fig. : 2 variable K-Map (ref. 1)

The only way to group 4 adjacent min terms.

The possible combinations are {(m0, m1), (m2, m3), (m0, m2) and (m1, m3)}.

3 Variable K-Map

It has 8 number of cells since the number of variables is 3.

The 3 variable K-Map is:

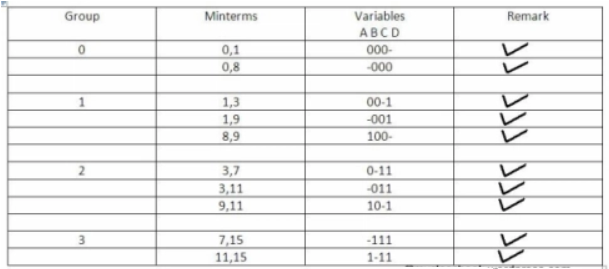
Fig. : 3 variable K-Map

The only way to group 8 adjacent min terms.

The possible are {(m0, m1, m3, m2), (m4, m5, m7, m6), (m0, m1, m4, m5), (m1, m3, m5, m7), (m3, m2, m7, m6) and (m2, m0, m6, m4)}.

The possible combinations of grouping 2 adjacent min terms are {(m0, m1), (m1, m3), (m3, m2), (m2, m0), (m4, m5), (m5, m7), (m7, m6), (m6, m4), (m0, m4), (m1, m5), (m3, m7) and (m2, m6)}.

If x=0, then 3 variable K-map becomes 2 variable K-map.

4 Variable K-Map

It has 16 number of cells since the number of variables is 4.

The 4 variable K-Map is:

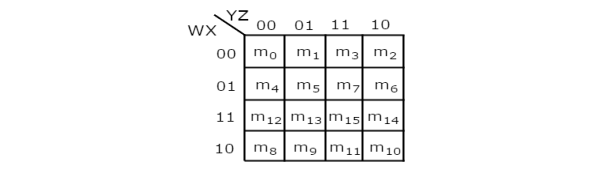
Fig. : 4 variable K-Map

The only way to group 8 adjacent min terms.

Let R1, R2, R3 and R4 represents the min terms of first row, second row, third row and fourth row respectively.

Similarly, C1, C2, C3 and C4 represents the min terms of first column, second column, third column and fourth column respectively.

The possible combinations are {(R1, R2), (R2, R3), (R3, R4), (R4, R1), (C1, C2), (C2, C3), (C3, C4), (C4, C1)}.

If w=0, then 4 variable K-map becomes 3 variable K-map.

Rules for simplifying K-maps:

Selecting K-map on the basis of number of variables present in the Boolean function.

If the Boolean function is in Max terms form, then place the zeroes at respective Max term cells in theK-map.

If the Boolean function is in PoS form, then place the zeroes wherever required in K-map for which the given sum terms are valid.

The maximum possibilities of grouping is checked for adjacent zeroes.

It should be of powers of two.

Starting from highest power of two and to the least power of two.

Highest power is equivalent to the number of variables considered in K-map and least power is zero.

Each group will give either a literal or one sum term.

It is known as prime implicant.

The prime implicant is an essential prime implicant when at least a single ‘0’ is not covered with any other groups but only that grouping covers.

The simplified Boolean function contains all essential prime implicants and only the required prime implicants.

Numericals

Simplify f(X,Y,Z)=∏M(0,1,2,4)f(X,Y,Z)=∏M(0,1,2,4)using K-map.

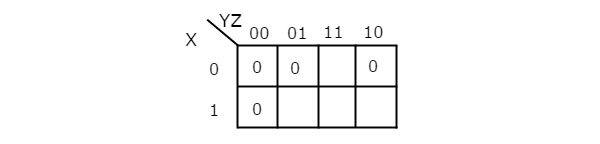
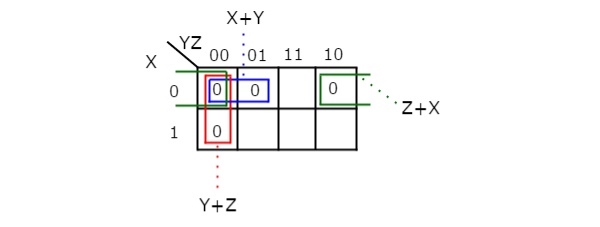
Prime Implicants ungrouped

Therefore, the simplified Boolean function is

f = (X + Y).(Y + Z).(Z + X)

Simplify:

F(P,Q,R,S)=∑(0,2,5,7,8,10,13,15)

F = P’Q’R’S’ + PQ’R’S’ + P’Q’RS’ +PQ’RS’ + QS

F = P’Q’S’ + PQ’S’ + QS

F = Q’S’ +QS

Simplify:

F(A,B,C)=π(0,3,6,7)

F = A’BC +ABC +A’B’C’ +ABC’

F = BC + C’ ( A’B’ + AB )

Reference Books:

1. John Yarbrough, ―Digital Logic Applications and Design, Cengage Learning, ISBN – 13: 978-81-315-0058-3

2. D. Leach, Malvino, Saha, ―Digital Principles and Applications‖, Tata McGraw Hill, ISBN – 13:978-0-07-014170-4.

3. Anil Maini, ―Digital Electronics: Principles and Integrated Circuits‖, Wiley India Ltd, ISBN:978-81-265-1466-3.

4. Norman B & Bradley, ―Digital Logic Design Principles, Wiley India Ltd, ISBN:978-81-265-1258

Sign Up

Index

Notes

Highlighted

Underlined

Browse by Topics

Notes

Highlighted

Underlined