Unit – 1

Set Theory and Logic

1.1 Introduction and significance of discrete mathematics

Computer science is all about the study of problems and solving problems by some process. The main goal is to develop an algorithm (step by step list of some instructions in order to solve a certain problem).

According to K.H Rosen, discreet mathematics has more than one purpose but more importantly it equips computer science students with logical and mathematical skills.

By B.Miller and D. Ranum, A computing machine end is to develop an algorithm, a measure by step list of instructions in work outing a job. Algorithm are finite procedures that if followed will work out the job.

Discreet mathematics is the study of mathematics which deals on discreet structures like graphs, trees and networks.

It deals with discreet objects like integers and rational numbers which are separated from each other.

Discreet mathematics is the language of computer science.

The field of mathematics that are considered to be part of discrete mathematics include graph theory and the theory of computation. Topics in number theory such as congruence’s and recurrence relations are also considered part of discrete mathematics.

Theoretical computer science includes areas of Theoretical computer science includes areas of discrete mathematics relevant to computing. It draws heavily on graph theory and logic. Included within theoretical computer science is the study of algorithms for computing mathematical results. 

Theoretical computer science also includes the study of various continuous computational topics.

We study about the following topics under discreet mathematics-

1. Information theory

2. Mathematical logic

3. Set theory

4. Graph theory

5. Discreet probability theory

6. Number theory

7. Trees

8. Topology

1.2 Sets-(Cantorian set theory, axiomatic set theory, set operations, cardinality of sets, principal of inclusion and exclusion)

Sets- A set is a collection of well-defined objects which are called the elements or members of the set.

We generally use capital letters to denote sets and lowercase letters for elements.

If any element which exists in the set is to be denoted as-

Suppose an element ‘a’ is from a set X, then it is represented as- a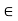X

Which means the element ‘a’ belongs to the set X.

If the element is not form the group then we use ‘not belongs to’.

Representation of sets-

There are two ways to represent sets.

1. In first way, the elements of the set are separated by comma and contained in the bracket-{  }.

2. The second way is that we define the characteristic of the element.

For example-

Suppose we have a set ‘A’ of all odd integers which are greater than 3.

Then we can represent it two ways-

1. A = {5, 7, 9…….}

2. A = {x | x is an odd integer, x>3 }

Subsets-

Let every element of set X is also an element of a set Y, then X is said to be the subset of Y.

Symbolically it is written as-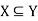

Which is read as- X is the subset of Y.

Note- If X = Y then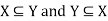

Proper sub-set-

A set X is called proper subset the set Y is-

1. X is subset of Y

2. Y is not subset of X

Note- every set is a subset to itself.

Equal sets-

If X and Y are two sets such that every element of X is an element of Y and every element of Y is an element of X, the set and set Y will be equal always.

We write it as X = Y and read as X and Y are identical.

Super set-

If X is a subset of Y, then Y is called a super set of X.

Null set-

A set which does not contain any element is known as null set.

We denote a null set by ∅

The null set is a subset of every set.

Singleton-

A set which has only one element is called singleton.

Example- A = {10} and B = {∅}

Theorem- if ∅ and ∅’ are empty sets then ∅=∅’

Proof: Let ∅≠ ∅’  then the following conditions must be true-

1. There is element x∈∅ such that x∉∅’

2. There is element x∈∅’ such that x∉∅.

but both these conditions are false since ∅’ and ∅’ has any elements if follows that ∅=∅’.

Operations on sets-

Union and intersection-

Union-We denote union of two sets as- A∪B, which is the set of all elements which belongs to A or to B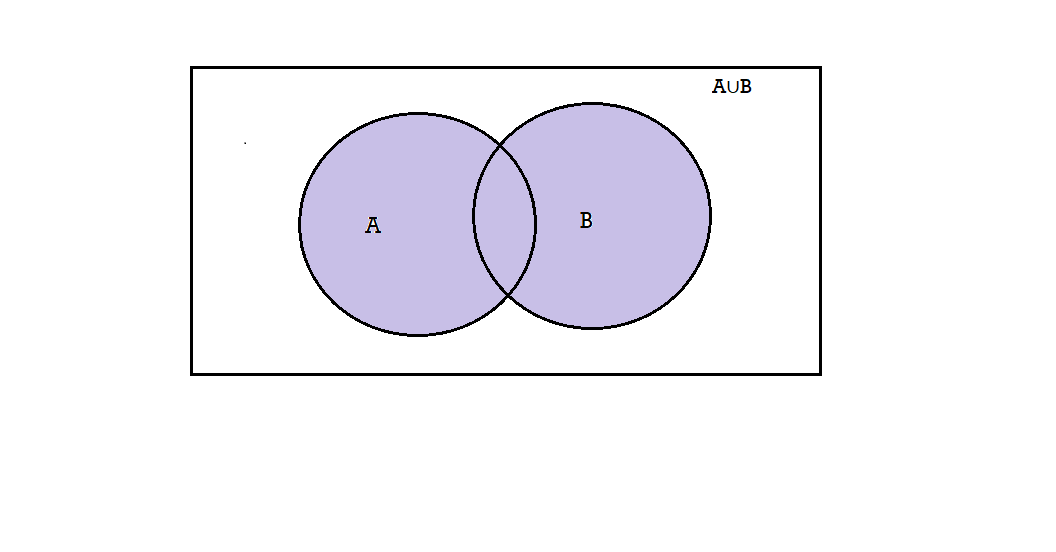                  

That is-

A∪B = {x |x∈∅Aor x∈∅B}

Intersection- We denote intersection of two sets as- A∩B, which is the set of all elements which belongs to A and to B.

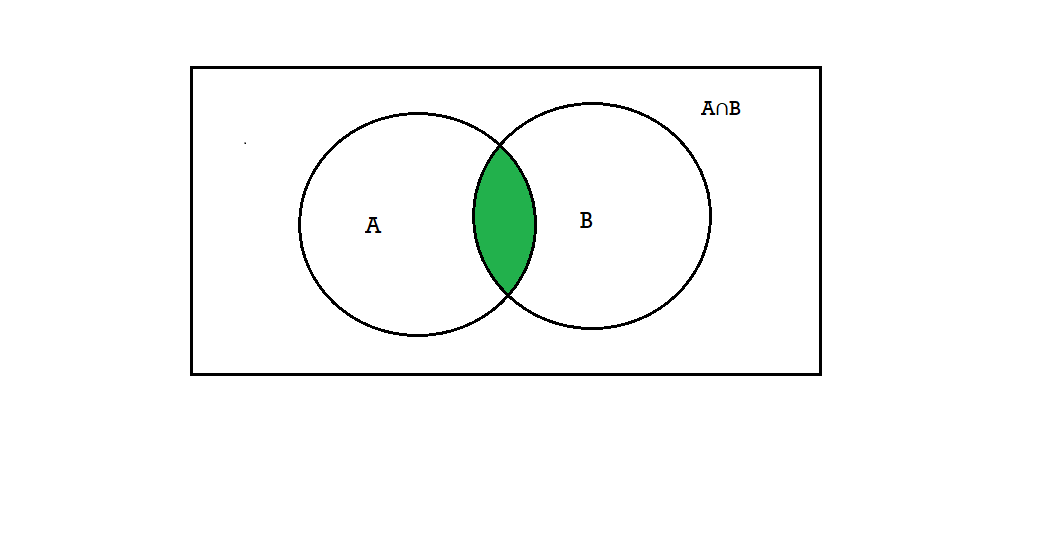
That is-

A∩B = {x |x∈∅A and x∈∅B }

Note- Two sets are said to be disjoint if they have no common elements in common.

 Example: If A = {1, 2, 3, 4, 5, 6}, B = {4, 5, 6, 7, 8, 9} and C = {5, 6, 7, 8, 9, 10}

Then-

A∪B = {1, 2, 3, 4, 5, 6,7, 8, 9}

A∪C = {1, 2, 3, 4, 5, 6,7, 8, 9,10}

B∪C = {4, 5, 6,7, 8, 9, 10}

A∩B = {4, 5, 6}

A∩C = {5, 6}

B∩C = {5, 6, 7, 8, 9}

Property-1-

An element x belongs to the union A∪B if x belongs to A or x belongs to B; hence every element

In A belongs to A ∪B, and every element in B belongs to A ∪B. That is,

 A ⊆A ∪B and B ⊆A ∪B

Property-2-

An element x belongs to the union A∪B if x belongs to A or x belongs to B; hence every element

In A belongs to A ∪B, and every element in B belongs to A ∪B. That is, A ⊆A ∪B and B ⊆A ∪B

Complements, differences and symmetric differences-

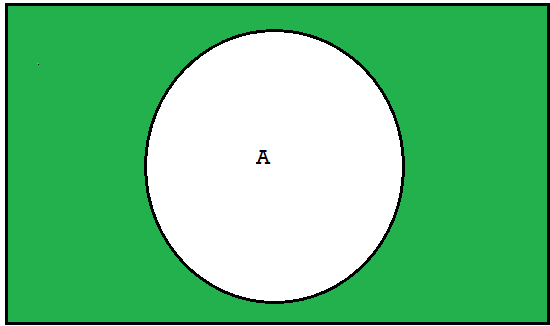
Complement-

The complement of a set A, denoted by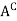 , is the set of elements which belong to U (universal set)but which do not belong to A. That is

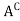= {x | x ∈U, x /∈A}

Difference-

The difference of A and B, denoted by A\B or A-B, is the set of elements which belong to A but which do not belong to B that is-

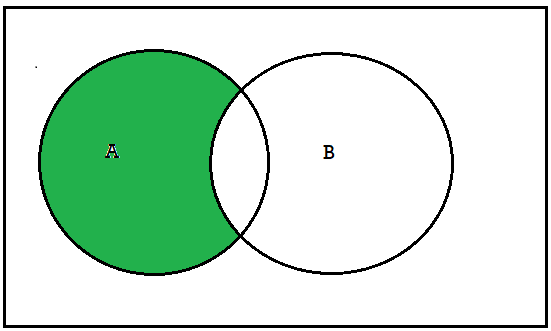
A-B = {x | x ∈A, x / ∈B}

The set A\Bor A-Bis read “A minus B”.

Symmetric difference-

The symmetric difference of sets A and B, denoted by A ⊕B, consists of those elements which belong to A or B but not to both. That is

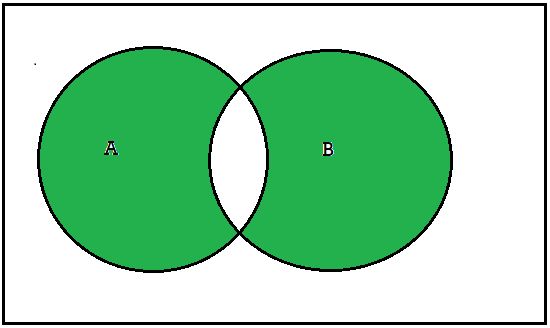
A ⊕B = (A ∪B)-(A ∩B) or A ⊕B = (A-B) ∪(B-A)

Cardinality of sets-

If A is finite set with n distinct elements, then n is called the cardinality of A. The cardinality of A is denoted by |A| [or by n (A)].

Example: Let A = {a, b, c, d}, then A is a finite set and |A| = 4

Cardinality of union of two sets-

Number of elements in A ∪B: (Cardinality of union) If A and B are any two finite sets then, the numbers of elements in A ∪B, denoted by | A ∪B | is given by | A ∪B | = | A | + | B | −| A ∩B |

Principal of inclusion and Exclusion-

Let we have A and B are finite sets. Then A ∪B and A ∩B are

Finite and

n(A ∪B) = n(A) + n(B) −n(A ∩B)

That is, we find the number of elements in A or B (or both) by first adding n(A) and n(B) (inclusion) and then

Subtracting n(A ∩B) (exclusion) since its elements were counted twice

For three sets-

n(A ∪B ∪C) = n(A) + n(B) + n(C) −n(A ∩B) −n(A ∩C) −n(B ∩C) + n(A ∩B ∩C)

1.3 Types of sets- (Bounded and unbounded sets, diagonalization argument, countable and uncountable sets, finite and infinite sets, countably infinite and uncountably infinite sets, power set)

The most familiar structure on a set S that defines boundedness is that of an order-

A binary relation "≤" that satisfies the conditions: 

Countable and uncountable sets-

A set S is said to be countable if it is either a finite set or countably infinite set.

A set is said to be uncountable otherwise.

Example-

Suppose we have a set of even natural numbers N = {2n: n∈N }. We can find a Bijection 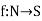with the formula 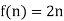. So we can say that the set is Countably infinite and also countable.

The set of odd natural numbers is also countably infinite.

Finite set-

If a set has finite number of elements then the set said to be a finite set.

Examples:

1. {2, 5, 9, 8, 11, 15, 19, 85}

2. The set of all vowels in English alphabets

3. The set of students in of high school in a particular school.

Infinite set-

If a set has infinite number of elements then the set said to be a infinite set.

Examples:

1. The set of all natural numbers.

2. The set of total points on a line.

Countably infinite and uncountably infinite sets-

Any set which can be put in a one-to-one correspondence with integers so that the prescription can be given for identifying its members one at a time is called a countably infinite set.

Any set which cannot be put in a one-to-one correspondence with integers is said to be uncoubtably infinite set.

Power sets-

The set of all subsets of a set A is called the power set of A.

The power set of A is denoted by P(A).

So that-

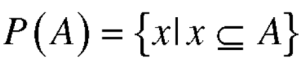
If A has n elements in it, then power set P(A) has 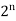elements.

Example: If A = {1, 2} then power set of A will be-

P(A) = {ϕ, {1}, {2}, {1, 2}}

1.4 Propositional logic- (logic, propositional equivalences, application of propositional logic- translating English sentences)

A proposition (or statement) is a declarative statement which is true or false, but not both.

Example-

(i) Ice floats in water.

(ii) China is in Europe

(iii) 2 + 2 = 4

(iv) 2 + 2 = 5

Compound proposition-

Many propositions are composite, that is, composed of sub-propositions and various connectives discussed

Subsequently such composite propositions are called compound Propositions. A proposition is said to be primitive

if it cannot be broken down into simpler propositions, that is, if it is not composite.

Following two propositions are composite:

“Roses are red and violets are blue.” and “John is smart or he studies every night.”

Basic logical operations-

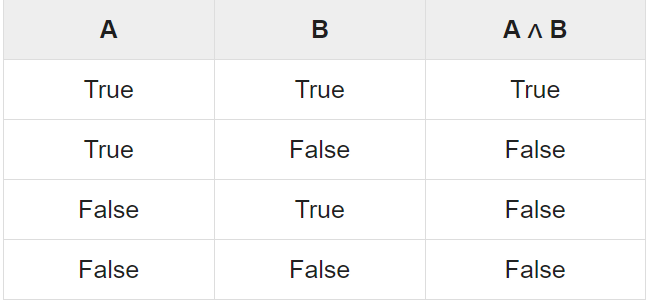
1. Conjunction- p ⋀ q

Any two propositions can be combined by the word “and” to form a compound proposition called the conjunction of the original propositions. Symbolically,

p ∧q

Read “p and q,” denotes the conjunction of p and q. Since p ∧q is a proposition it has a truth value, and this truth

Value depends only on the truth values of p and q.

Note- If p and q are true, then p ∧q is true; otherwise p ∧q is false.

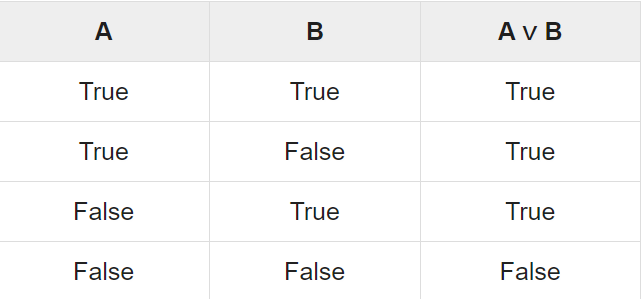
2. Disjunction, p ∨q

Any two propositions can be combined by the word “or” to form a compound proposition called the disjunction of the original propositions. Symbolically,

p ∨q

Read “p or q,” denotes the disjunction of p and q. The truth value of p ∨q depends only on the truth values of p

And q as follows-

If p and q are false, then p ∨q is false; otherwise p ∨q is true

Negation-

Given any proposition p, another proposition, called the negation of p, can be formed by writing “It is not true that . . .” or “It is false that . . .” before p or, if possible, by inserting in p the word “not.” Symbolically, the negation of p, read “not p,” is denoted by

￢p

The truth value of ￢p depends on the truth value of p as follows-

If p is true, then ￢p is false; and if p is false, then ￢p is true

Logical equivalences-

Two propositions P(p, q, . . .) and Q(p, q, . . .) are said to be logically equivalent, or simply equivalent and denoted by

P(p, q, . . .) ≡Q(p, q, . . .)

Note- the prepositions are logically equivalent.

Prepositions and truth tables-

Suppose P (p, q, . . .) denote an expression constructed from logical variables p, q, . . ., which take on the value

T or F which are true and false, and the logical connectives ∧, ∨, and ￢ and others. Such an expression P (p, q, . . .) will be called a proposition.

The main property of a proposition P(p, q, . . .) is that its truth value depends exclusively upon the truth values of its variables, that is, the truth value of a proposition is known once the truth value of each of its variables

is known. A simple concise way to show this relationship is through a truth table

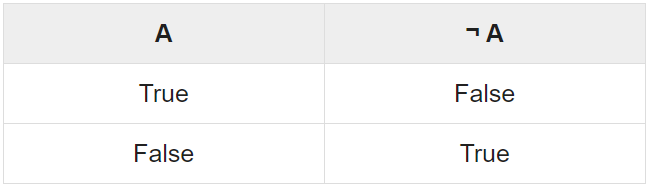
Laws of prepositions-

The prepositions satisfy the following rules

Tautologies-

A tautology is a formula which is always true for every value of its propositional variables-

Contradiction-

A Contradiction is a formula which is always false for every value of its propositional variables.

Contingency-

A Contingency is a formula which has both some true and some false values for every value of its propositional variables.

1.5 Proof by mathematical induction and strong mathematical induction

Mathematical induction is a mathematical technique is used to prove a statement, a theorem or a formula is true for every natural number.

The technique has two steps to prove any statement-

1. Base step (it proves that a statement is true for the initial value)

2. Inductive step (it proves that is the statement is true for n’th iteration then it is also true for 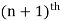iteration.

Example-1: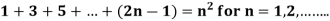

Sol. here for n = 1,     1 = 1²

Now let us assume that the statement is true for n = k

Hence we assume that 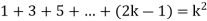is true.

Now we need to prove that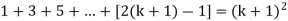

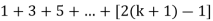
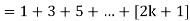
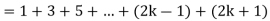
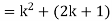
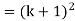
So that 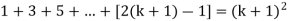which satisfies the second step.

Hence-

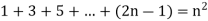
Example-2: Prove 1+2+...+n=n(n+1)/2 using a proof by induction

Sol.

Let n=1: 1 = 1(1+1)/2 = 1(2)/2 = 1 is true,

Step-1: Assume n=k holds: 1+2+...+k=k (k+1)/2

Show n=k+1 holds: 1+2+...+k+ (k+1) = (k+1)((k+1)+1)/2 

Substitute k with k+1 in the formula to get these lines. Notice that I write out what I want to prove.

Step-2: Now start with the left side of the equation

1+2+...+ (k+1) =1+2+...+k+ (k+1)

=k (k+1)/2 + (k+1)

= (k (k+1) + 2(k+1))/2 by 2/2=1 and distribution of division over addition

= (k+2) (k+1)/2 by distribution of multiplication over addition

= (k+1) (k+2)/2 by commutativity of multiplication

Strong inductions-

It is another form of mathematical induction. By using this  we can prove that a propositional function, P(n) is true for all positive integers n.

Working steps-

1. Base step- this proves that the initial proposition P(1) is true.

2. it proves that the conditional statement[P(1)∧P(2)∧P(3)∧⋯∧P(k)]→P(k+1) is true for positive integers k.