Unit – 3
Counting Principle
Sum rule-
Suppose S be a set and | S | denote the number of elements in S.
If S is a union of disjoint non-empty subsets
A1, A2,…,An then
|S| = |A1| + |A2| + … + |An|
In the above statement the subsets Ai of S are all disjoint i.e., they have no element in common. If Ai
A nd Aj an two subsets of S, then
Ai ∩Aj= ∅i≠j
And we have
S = A1 ∪A2 ∪A3 ∪... ∪An
That is each element of S is exactly in one of the subsets Ai. In other words, the subsets A1, A2,…An is a partition of S. We now state the sum rule for counting events.
Let S be a sample space. Two events E1 and E2 of X are said to be mutually exclusive if the events have no elements in common. If E1, E2, E3, …En, are mutually exclusive events of S, then we can state
Sum rule for counting events as follows:
If E1, E2… En are mutually exclusive events of a sample space S and E1 can happen in m1 ways. E2 can happen in m2 ways…
En can happen in mn ways then E1 or E2 or … or En can happen m1 + m2 + …
+ mn ways.
Sum rule principle-
Let A and B are two disjoint sets, then-
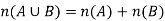
Product rule principle-
Let A×B is the Cartesian product of two sets A and B, then-
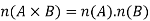
Example-1: How many ways can we draw a club or a diamond from a pack of cards?
Solution: As we know that there are 13 clubs and 13 diamonds in a pack of cards.
The number of ways a club or a diamond may be drawn 13 + 13 = 26.
Example-2: In how ways can be drawn an ace or a king from an ordinary deck of playing cards?
Solution:
Number of Aces in a pack = 4
Number of kings in a pack = 4
Number ways an Ace or a king can be drawn from the pack = 4 + 4 =
Product rule-
If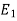 
, 
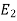, …, En are events, and E can happen in 
ways 
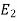can happen 
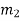ways, … 
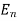can happen in 
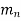ways, then the sequence of events E, first followed by 
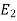followed by 
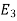, …, followed by 
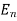can happenin m1 × m2 × … × mn ways
Example-1: In how many different ways one can answer all the questions of a true-false test consisting of 4 questions?
Solution: There are two ways of answering each of the 4 questions. Therefore by product rule the
Number of ways in which all the 4 questions can be answered-
= 2 × 2 × 2 × 2 = 16
Permutations-
A permutation of n objects taken r at a time is an arrangement of r of the objects
(r≤n).
The symbols of permutations of n things taken r at a time are-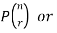
Example 1: Consider the three letters x, y, z. The arrangements of the letter x, y, ztaken two at a time are-
xy, yx, xz, zx, yz, zy
∴The number of 2-arrangements are 6 i.e., the number of permutation of 3 letters taken 2 at a time
Note-A permutation of n objects taken r at a time is also called r-permutation
Factorial function-
The product of the positive integers from 1 to n is deoted by n!and we read it as “factorial “
Expressed as-
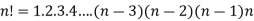
Note-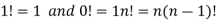 
Binomial coefficient-
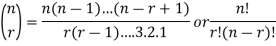
Example:
1. 
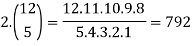
Permutation-
The arrangement of a set of n objects in a given order is called a permutation.
Any arrangement of any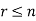 
of these objects in a given order is said to be r-permutation.
The number of permutations of n objects taken r will be denoted as-
P(n, r)
Formula-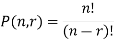 
Permutation with repetitions-
The number of permutations of n objects of which are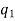 
are alike, 
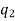are alike,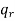 
are alike is-
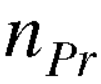
Sampling with or without replacement-
Suppose we chose the samples with repetition, fro example if we draw a ball from a urn then we put back that ball in the urn and again we pick a ball and we continue the process, so this is the case of sampling with repetition
Then the product rule tells us that the number of such samples is-
n.n.n.n.n……….n.n =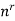 
And if we pick a ball from the urn and we do not put it back to the urn, then this is the case of sampling without replacement.
So that in this case the number of samples are given as-
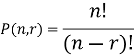
Example-
Three cards are chosen one after the other from a 52-card deck. Find the number m of ways
This can be done: (a) with replacement; (b) without replacement.
Sol.
(a) Each card can be chosen in 52 ways. Thus m = 52(52)(52) = 140 608.
(b) Here there is no replacement. Thus the first card can be chosen in 52 ways, the second in 51 ways, and the third in 50 ways. So that-
P(52, 3) = 52(51)(50) = 132 600
Example-
There are 4 black, 3 green and 5 red balls. In how many ways can they be arranged in a row?
Solution: Total number of balls = 4 black + 3 green + 5 red = 12
The black balls are alike,
The green balls are, and the red balls are alike,
The number of ways in which the balls can be arranged in a row =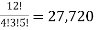
Example- A box contains 10 light bulbs. Find the number n of ordered samples of:
(a) Size 3 with replacement,
(b) Size 3 without replacement.
Solution:
(a) n=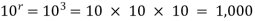 
(b) P (10, 3) = 10 × 9 × 8 = 720
Circular permutations-
A circular permutation of n objects is an arrangement of the objects around a circle.
If the n objects are to be arranged round a circle we take an objects and fix it in one position.
Now the remaining (n – 1) objects can be arranged to fill the (n – 1) positions the circle in (n – 1)! ways.
Hence the number of circular permutations of n different objects = (n – 1)!
Combinations-
A combination of n objects taken at a time is an unordered selection of r of the n
Objects (r ≤n).
A combination of n objects taken r at a time is also called r-combination of n objects.
The number of combinations is given by-
C(n, r)
Note-
1. property-1
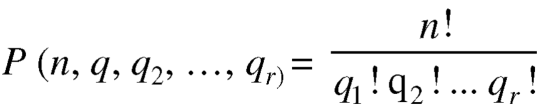
2. property-2
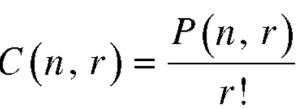
3. property-3
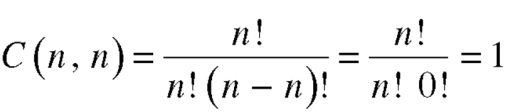
The numbers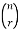
are called the binomial coefficients.
Binomial theorem-
Binomial theorem gives a formula for the coefficients in the expansion of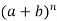 
.
According to theorem-
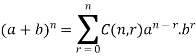
Example-1: Expand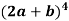 
Sol.
Here we have-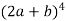
By using binomial theorem, we get
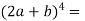
Example-2: Find the term containing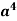 
in the expansion of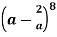 
Sol.
The general term will be-
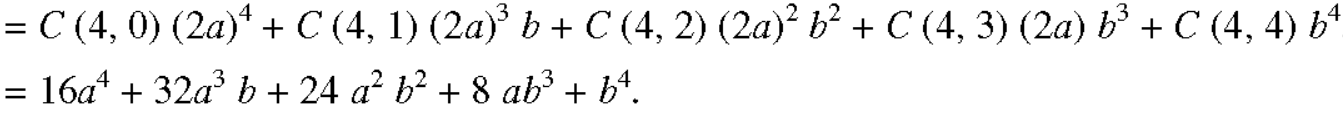
Put 8 – 2r = 4 we get r = 2
Therefore the term contain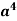s
is-
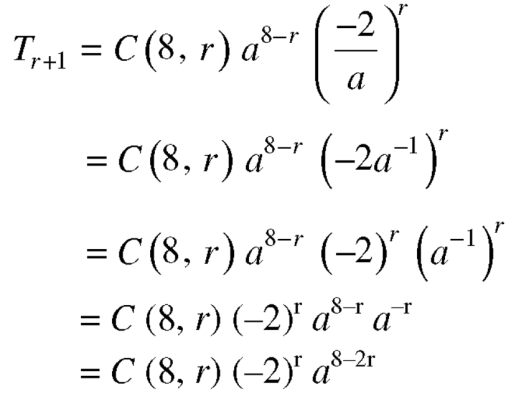
Note-
If we replace ‘a’ and ‘b’ by ‘x’ and ‘1’ then we get an another form of the binomial theorem-
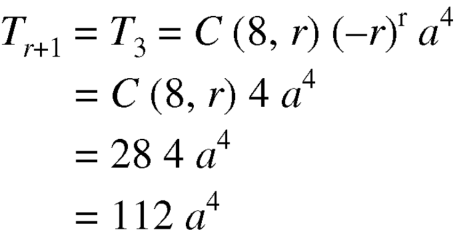
Example-3: In the expansion of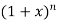 
, prove the following result-
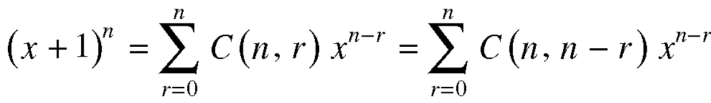
Sol. We have-
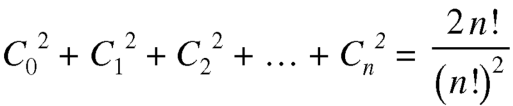
As we know that the coeff. of the terms equivalent from the beginning and end are equal, so that-
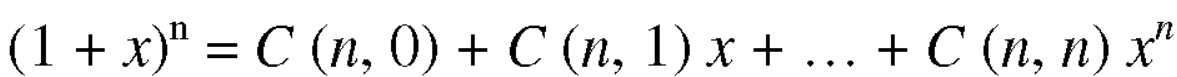
By multiplying the above two equations, we get-
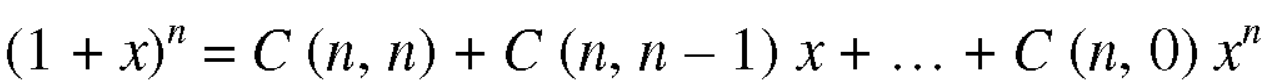
From RHS, we see the coeff. of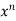
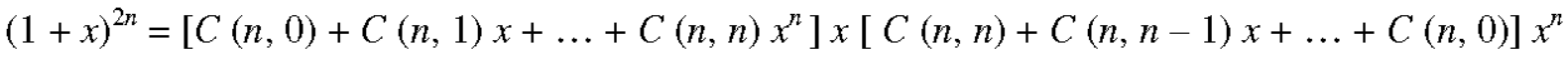
But the coeff. of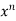
in 
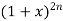is-
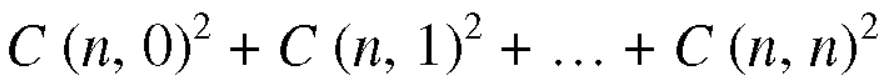
Note-
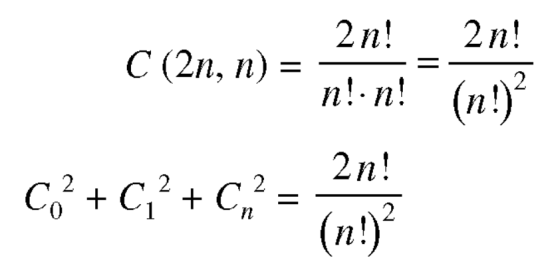
And
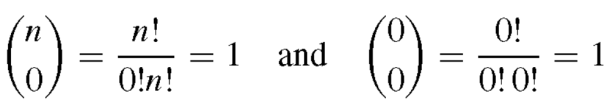
Generalized sum rule-
If we have tasks 
that can be done in 
ways respectively, and no two of these tasks can be done at the same time then there are 
ways to do one of these task.
Generalized product rule-
If we have sequential task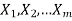 
that can be done in 
, then there are 
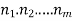to do the procedure.
Permutation and combination with unlimited repetitions-
Suppose U (n, r) denotes r-permutations of n-objects with unlimited repetitions and v (r, n) denotes the r-combination with unlimited repetitions, then-
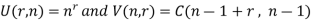
Let us consider a set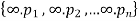 
where 
are all distinct.
Any r-combination is of the form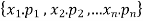 
here each 
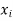is a non-negative integer and 
The numbers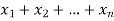 
are called repetition numbers. Conversely any sequence of non-negative integers-
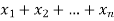
Corresponds to a r-combination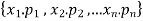 
.
The following observation we get-
The number of r-combination of 
= the number of non-negative integer solution of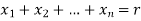 
= the number of ways of placing r indistinguishable balls in n numbered boxes.
= the number of binary numbers with n – 1 one’s and zeros.
= C (n – 1 + r, r)
= C (n – 1 + r, n - 1)
Example: Find the number of non-negative integral solutions to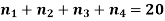 
Sol: We have n = 4, r = 20
The number of non-negative integral solutions
= C (4 – 1 + 20, 20)
= C (23, 20)
= 1,771
Example-Find the number of ways of placing 8 similar balls in 5 numbered boxes.
Solution:
The number of ways of placing similar balls in 5 numbered boxes is
= C (5 – 1 + 8, 8)
= C (12, 8) = 495
Example-How many outcomes are possible by costing a 6 faced die 10 times?
Solution:
This is same as placing 10 similar balls into 6 numbered boxes.
There are C (6 – 1 + 10, 10)
= C (15, 10) possible outcomes.
Generating permutations in lexicographic order-
Generating the permutations of the n smallest positive integers and then replacing those integers with any set of n elements will create the set of permutations for that set. Often, the permutation of a set will be given in lexicographic ordering.
The lexicographic ordering for a set of permutations {1,2,3,...,n-1,n} has the permutation a1a2...an precede the permutation b1b2...bn when, for some k, 1 <= k <= n, a1 = b1, a2 = b2, ..., ak-1 = bk-1, and ak < bk.
A procedure for generating the next permutation in lexicographic order can be developed for a given a1a2...an. If an-1 < an, swap the two to get the next largest permutation (56.. to ...65). If an-1 > an, then a larger permutation cannot be made from the two integers. In that case, look at the final three integers. If an-2 < an-1, then put the smaller of the two integers an-1 and an in the an-2 position. Fill the remaining positions in lexicograpic order to complete the permutation (..165 to ...516).
This procedure can be generalized to produce the next largest permutation for any a1a2...an.
Generating the Next Largest Permutation in Lexicographic Order
Next Permutation(a1a2...an; permutation of {1, 2,..., n} != to n, (n-1),...2, 1)
{
j = n -1;
while (a[j] > a [j+1])
{j = j - 1;}
k = n;
while (a[j] > a[k])
{k = k -1;}
swap a[j] and a[k];
r = n;
s = j + 1;
while (r > s)
{
swap a[r] and a[s];
r = r - 1;
s = s + 1;
}
Generating combinations in lexicographic order-
For any r-combination, a procedure for creating the next largest combination can be developed.
A combination a1a2...ar in lexicographic order is given for a set {1,2,3,...,n}. In the set {1, 2, 3, 4, 5, 6}, a 4-combination could be {1, 2, 5, 6}.
To obtain the next largest combination, find the last ai in the combination so that ai != n - r + i. (The last element in the combination with ai != n - r + i is 2.) Replace ai with ai + 1, and aj with aj + j - i + 1, for j = i +1, i + 2, ..., r. (This creates the next largest combination, {1, 3, 4, 5}.
Generating the Next Largest r-Combination in Lexicographic Order
Next combination(a1a2...ar; subset of {1, 2,..., n} != to {(n-r+1,...,n} with a1 <a2<...<ar)
{
i = r;
while (a[i] > n - r + i)
{i = i - 1;}
a[i] = a[i] + 1;
for (j = i + 1; j <= r; j++)
{a[j] = a[i] + j - i;}
}
Describe an algorithm for generating all the combinations of the set of the n smallest positive integers-
