Unit-VI
Algebraic Structures and Coding Theory
By a property of an algebraic structure, we mean a property possessed by any of its operations. Important properties of an algebraic system are:
1. Associative and commutative laws
An operation * on a set is said to be associative or to satisfy the associative law if, for any elements a, b, c in S we have (a * b) * c = a * (b * c )
An operation * on a set S is said to be commutative or satisfy the commutative law if, a * b = b * a for any element a, b in S.
2. Identity element and inverse
Consider an operation * on a set S. An element e in S is called an identity elements for * if for any elements a in S - a * e = e * a = a
Generally, an element e is called a left identity or a right identity according to as e *a ora * e = a where a is any elements in S.
Suppose an operation * on a set S does have an identity element e. The inverse of an element in S is an element b such that: a* b = b * a = e
3. Cancellation laws:An operation * on a set S is a said to satisfy the left cancellation law if, a * b = a * c implies b = c and is said to satisfy the right cancellation law if, b * a = c * a implies b = c
An algebraic system is an object A = (A, O, R) consisting of a non-empty set A. a family O of algebraic operations Oi: Ani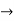 A (i
A (i 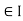 ) and a family R of relations rj
) and a family R of relations rj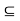 Amj (j
Amj (j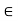 J) defined on A. Theindices ni, mj of the Cartesian powers of A under the consideration are assumed to be non-negative integers and are said to be arities of the respective operations and relations. The set A is called the Cartesian set or underlying set of algebraic system A. while its elements are called the elements of this system. The cardinality
J) defined on A. Theindices ni, mj of the Cartesian powers of A under the consideration are assumed to be non-negative integers and are said to be arities of the respective operations and relations. The set A is called the Cartesian set or underlying set of algebraic system A. while its elements are called the elements of this system. The cardinality 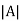 of A is said to be the cardinality of A or the order of the algebraic system A. The image Oi (
of A is said to be the cardinality of A or the order of the algebraic system A. The image Oi (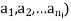 of the element (
of the element (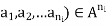
Under the mapping Oi : 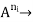 Ais called the value of operation Oi at the point (
Ais called the value of operation Oi at the point (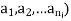 .similarly, if (
.similarly, if (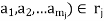 , then one says that the elements (
, then one says that the elements (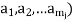 of A are in relation
of A are in relation 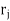 , and one writes
, and one writes 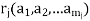 .The operations Oi ( i
.The operations Oi ( i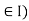 and the relation
and the relation 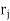 ( j
( j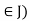 , unlike other operations and relations that may be defined on A , are called basic operation primitive.
, unlike other operations and relations that may be defined on A , are called basic operation primitive.
Example1: solve the following system of equations
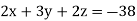 …(1)
…(1)
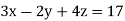 …..(2)
…..(2)
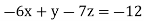 ….(3)
….(3)
Solution:
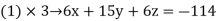
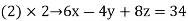
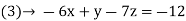
By solving the above equations we get
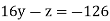
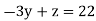
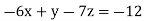
Solving for z we get
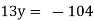
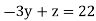
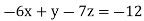
We get y = -8
By putting y value in above equation we get z=-2
And inserting both the equations we solve for x, we get x= 3
Therefore the solution to the system of equation is x = 3, y = -8, z = -2
Semi-group: An algebraic structure which satisfies closure and associative property is said to a semi-group
i.e.
Closure: (a*b) S to s for all a,b 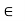 to S
to S
Associative property: a*(b*c) 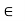 to S for all a, b, c
to S for all a, b, c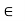 to S
to S
Monoids:An algebraic structure which satisfies closure, associative property and identity is said to be a monoid.
Closure: (a*b) 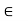 to S for all a, b
to S for all a, b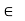 to S
to S
Associative property: a*(b*c) to 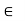 S for all a, b, c
S for all a, b, c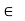 to s.
to s.
Identity element: There exists e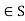 such that e*a = a*e
such that e*a = a*e 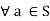
Groups: An algebraic structure which satisfies closure, associative, identity and inverse properties is said to be a group.
Closure: (a*b) 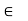 to S for all a, b
to S for all a, b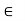 to S
to S
Associative property: a*(b*c) to 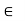 S for all a, b, c
S for all a, b, c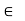 to s.
to s.
Identity property: There exists e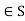 such that e*a = a*e
such that e*a = a*e 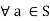
Inverse property: there exists a, a-1 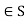 such that a * a-1 = a,
such that a * a-1 = a, 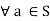
Example1: Let S=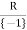 . Define * on S by a*b =a+ b+ ab
. Define * on S by a*b =a+ b+ ab
(a) Show that * is a binary operation on S.
(b) Show that [S,*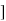 is a group.
is a group.
(c) Find the solution of the equation 2*x*3= 7 in S
Solution: (a) We must show that S is closed under *, that is , that a+b+ab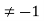 for a,b
for a,b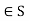 .Now a+b+ab=-1 if and only if 0=ab+a+b+1=(a+1)(b+1).This is the case if and only if either a=-1 or b = -1 , which is not the case for a,b
.Now a+b+ab=-1 if and only if 0=ab+a+b+1=(a+1)(b+1).This is the case if and only if either a=-1 or b = -1 , which is not the case for a,b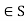 .
.
(b) We have a*(b*c) = a*(b+c+bc) = a+(b+c+bc)+a(b+c+bc)=a+b+c+ab+ac+bc+abc and (a*b)*c = (a+b+ab)*c =(a+b+ab)+c+(a+b+ab) = a+b+c+ab+ac+bc+abc. Thus * is associative. Note that 0 acts as identity element for * , since 0*a =a*0=a.
Also, 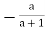 acts as inverse of a, for a*
acts as inverse of a, for a* 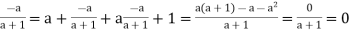
Thus [s,*] is a group.
(c)Because the operation is commutative, 2*x*3=2*3*x=11*x. Now the inverse of 11 is 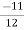 , bypart(b) . From 11*x=7, we obtain
, bypart(b) . From 11*x=7, we obtain
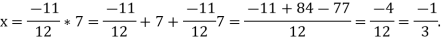
Example 2: Let G be a group with a finite number of elements. Show that for any 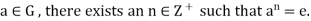
Solution: Let G has m elements, Then the elements e , a,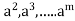 are not all different ,since G has only m elements . If one of e , a
are not all different ,since G has only m elements . If one of e , a 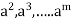 is e ,then we are done . If not, then we must have
is e ,then we are done . If not, then we must have 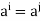 where i<j, Repeated left cancellation of a yields e=
where i<j, Repeated left cancellation of a yields e=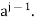
Homomorphism: In mathematics, an algebra homomorphism is an homomorphism between two associative algebras, More precisely, if A and B, are algebras over a field (or commutative ring ) K , it is a function F:A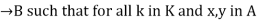
The first two conditions say that F is a module homomorphism.
If F admits an inverse homomorphism, or equivalently if it is bijective, F is said to be an isomorphism between A and B.
Normal Sub Group: A Subgroup N of a group G is called a Normal Subgroup of G if it is invariant under conjugation that is the conjugation of an element of N by an element of G is always in N. The usual notation for this relation is N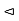 G, and the definition may be written in symbol as
G, and the definition may be written in symbol as
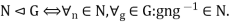
Congruence Relations: If a and b are integers and m is a positive integer, them a is congruent to b modulo m if m divides a-b.
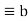
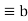
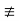
Example 1: Let 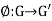 be a group homomorphism , and let H=ker(
be a group homomorphism , and let H=ker(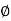 ).Let a
).Let a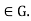 Then , the set
Then , the set 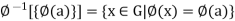 is the left coset aH of H, and is also the right coset Ha of H , Consequently , the two partitions of G into left cosets and into right cosets of H are the same.
is the left coset aH of H, and is also the right coset Ha of H , Consequently , the two partitions of G into left cosets and into right cosets of H are the same.
Proof: (a) It is a homomorphism, because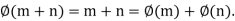
(b) It is not a homomorphism, because 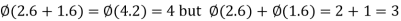 .
.
(c) It is a homomorphism, because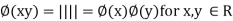 *
*
(d) It is a homomorphism, because 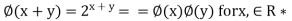
Example 2: The following are three equivalent conditions for a subgroup H to be a normal subgroup of a group G.
1.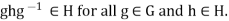
2.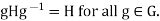
3.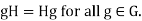
Proof: (1)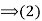 Suppose that H is a subgroup of G such that
Suppose that H is a subgroup of G such that 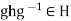 for all g
for all g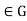 and all h
and all h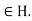 Then
Then 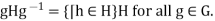
We claim that actually 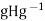 =H .We must show that H
=H .We must show that H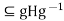 for all g
for all g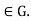
Let h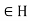 . Replacing g by
. Replacing g by 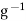 in the relation
in the relation 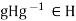 , we obtain
, we obtain 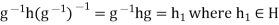 .
.
Consequently,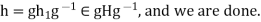
(3)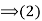 Suppose that gH=Hg for all g
Suppose that gH=Hg for all g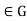 . Then
. Then 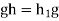 , So
, So 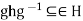 for all g
for all g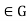
And all 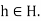 By the preceding paragraph, this means that
By the preceding paragraph, this means that 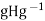 =H for all g
=H for all g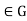 .
.
(2)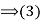 Conversely, if
Conversely, if 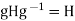 for all g
for all g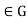 then
then 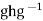 =
=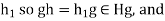 gH
gH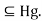 But also,
But also, 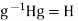 giving
giving 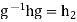 ,so that hg=g
,so that hg=g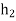 and Hg
and Hg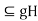 .
.
Example:3 Prove that congruence modulo n is an equivalence relation on Z.
Solution:
1) Reflexivity: For any a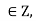 we have
we have 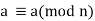 because a-a = 0 is divisible by n.hence relation is reflexive.
because a-a = 0 is divisible by n.hence relation is reflexive.
2) Symmetry: suppose a  b(mod n)
b(mod n)
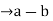 is divisible by n
is divisible by n 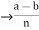 = k, for some k
= k, for some k 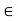 z
z 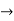 a-b = nk
a-b = nk
Therefore, b-a = -(a-b) = -nk= n(-k)
Thus the relation is symmetric.
3) Transitivity: Suppose a  b (mod n) and b
b (mod n) and b  c (mod n), then
c (mod n), then 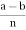 = k and
= k and 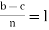
By adding this two equations we get, a-c = n(k+1) 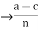 = k+l
= k+l
So a-c is divisible by n as k+1 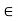 Z, i.e., a
Z, i.e., a  c (mod n)
c (mod n)
Thus the relation is transitive.
Hence this is an equivalence relation on Z.
Ring: A Ring 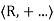 is a set R together with two binary operations + and .., called addition and multiplication, defined on R such that the following axioms are satisfied
is a set R together with two binary operations + and .., called addition and multiplication, defined on R such that the following axioms are satisfied
(1)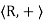 is an abelian group,
is an abelian group,
(2) Multiplication is associative,
(3) For all a,b,c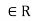 ,the left distributive law, a.(b+c)=a.b+a.c and the right distributive law (a+b).c=a.c+b.c hold.
,the left distributive law, a.(b+c)=a.b+a.c and the right distributive law (a+b).c=a.c+b.c hold.
Integral Domains: We know that the product of any two non-zero integers is always nonzero. But this may not be the case of arbitrary rings. For example, consider the ring 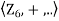 . Note that product of two nonzero elements may be zero in this ring, for instance 2.3=0 in
. Note that product of two nonzero elements may be zero in this ring, for instance 2.3=0 in 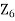 . We call these type of elements as 0 divisors.
. We call these type of elements as 0 divisors.
Field: A nonzero commutative ring in which every nonzero element has a multiplicative inverse is called a field.
Example1: The cancellation laws hold in a ring R if and only if R has no divisors of 0.
Proof: Assume that R is a ring in which the cancellation laws hold and let ab=0 for some a,b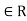 .If a
.If a by right cancellation law .Thus R has no divisors of 0, if the cancellation laws hold in R.
by right cancellation law .Thus R has no divisors of 0, if the cancellation laws hold in R.
Conversely, suppose that R has no divisors of 0, and suppose that ab=ac, with a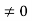 . Since a
. Since a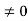 and since R has no divisors of 0, we have 0=ab-ac=a(c)
and since R has no divisors of 0, we have 0=ab-ac=a(c) 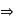 b-c =0
b-c =0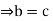 .In similar way, b a=ca with a
.In similar way, b a=ca with a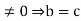 . Thus if R has no divisors of 0, the cancellation laws hold in R.
. Thus if R has no divisors of 0, the cancellation laws hold in R.
Example 2: Every field F is an integral domain.
Proof: Let 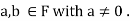 Assume that ab=0 .Since
Assume that ab=0 .Since 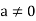 ,the multiplicative we
,the multiplicative we
Inverse 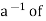 a exists , multiplying the above equation on both sides by
a exists , multiplying the above equation on both sides by 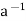 , weget
, weget
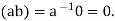 Hisimplies, 0=
Hisimplies, 0=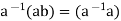 b=eb=b, which shows that F has
b=eb=b, which shows that F has
No divisors of 0. Since F is a field, in particular F is a commutative ring with unity, and we showed that F has no divisors of 0. Hence F is an integral domain.
We know that Z is an integral domain, but not a field. We next prove that finite integral domains are fields.
Example 3: Consider the map det of 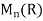 into R where det(A) is the determinant of the matrix A for A
into R where det(A) is the determinant of the matrix A for A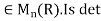 a ring homomorphism ? Justify your answer.
a ring homomorphism ? Justify your answer.
Solution: Because det(A+B) need not equal det(A)+det(B) , we say that det is not a ring homomorphism .For example ,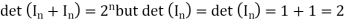
Coding theory: Coding theory is the study of the properties of codes and their respective fitness for specific applications. Codes are used for data compression, cryptography, error detection and correction, data transmission and data storage. Codes are studied by various scientific disciplines—such as information theory, electrical engineering, mathematics, linguistics, and computer science—for the purpose of designing efficient and reliable data transmission methods. This typically involves the removal of redundancy and the correction or detection of errors in the transmitted data.
There are four types of coding:
Data can be seen as a random variable X: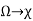 , where x
, where x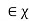 appears with probability
appears with probability 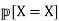
Data are encoded by strings (words) over an alphabet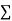
 .
.
A code is a function
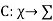 *(or
*(or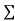 +if the empty string is not part of the alphabet).
+if the empty string is not part of the alphabet).
C (x) is the code word associated with x .
.
Length of the code word is written as l(C(x)) .
.
Expected length of a code is
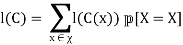
The concatenation of code words .
.
The code word of the empty string is the empty string itself: 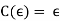
Polynomial rings:The polynomial ring, K[X], in X over a field (or, more generally, a commutative ring) K can be defined[1] (there are other equivalent definitions that are commonly used) as the set of expressions, called polynomials in X, of the form
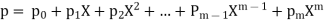

where p0, p1, ..., pm, the coefficients of p, are elements of K, pm ≠ 0 if m> 0, and X, X2, ..., are symbols, which are considered as "powers" of X, and follow the usual rules of exponentiation: X0 = 1, X1 = X, and 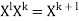 for any nonnegative integersk and l. The symbol X is called an indeterminate or variable. (The term of "variable" comes from the terminology of polynomial functions. However, here, X has not any value (other than itself), and cannot vary, being a constant in the polynomial ring.)
for any nonnegative integersk and l. The symbol X is called an indeterminate or variable. (The term of "variable" comes from the terminology of polynomial functions. However, here, X has not any value (other than itself), and cannot vary, being a constant in the polynomial ring.)
Two polynomials are equal when the corresponding coefficients of each Xk are equal.
One can think of the ring K[X] as arising from K by adding one new element X that is external to K, commutes with all elements of K, and has no other specific properties. (This may be used for defining polynomial rings.)
The polynomial ring in X over K is equipped with an addition, a multiplication and a scalar multiplication that make it a commutative algebra. These operations are defined according to the ordinary rules for manipulating algebraic expressions. Specifically, if
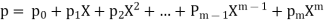
and
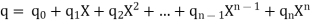
then
p+q = 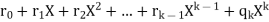

and
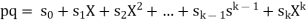

wherek = max(m, n), l = m + n,
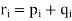
and
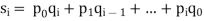
In these formulas, the polynomials p and q are extended by adding "dummy terms" with zero coefficients, so that all pi and qi that appear in the formulas are defined. Specifically, if m<n, then pi = 0 for m<i ≤ n.
The scalar multiplication is the special case of the multiplication where p = p0 is reduced to its constant term (the term that is independent of X); that is
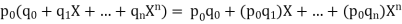

It is straightforward to verify that these three operations satisfy the axioms of a commutative algebra over K. Therefore, polynomial rings are also called polynomial algebras.
Polynomial code:In coding theory, a polynomial code is a type of linear code whose set of valid code words consists of those polynomials (usually of some fixed length) that are divisible by a given fixed polynomial (of shorter length, called the generator polynomial).
Example1: Find the following binary operation by using code theory.
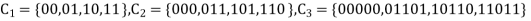
Solution: 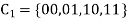
Is a binary [2,2] code for 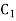 with generator matrix is
with generator matrix is
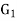 =
=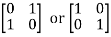 or…..
or…..
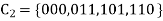
Is a binary [3,2] code for 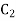 with generator matrix is
with generator matrix is
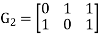
And 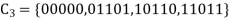
Is a binary [5,2] code for 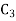 with generator matrix is
with generator matrix is
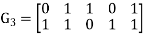
Example 2: Consider the polynomial code over GF(2)={0,1} with n=5 , m=2 and generator polynomial 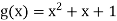 , This code consists of the following code words.
, This code consists of the following code words.
Solution 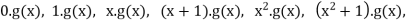
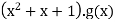
Or written explicitly:
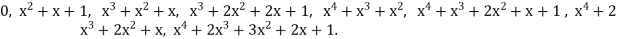
Since the polynomial code is defined over the Binary Galois Field GF(2)={0,1}, polynomial elements are represented as a modulo-2 sum and the final polynomials are:
0, 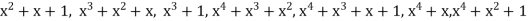
Equivalently, expressed as strings of binary digits, the code words are
00000, 00111, 01110, 01001, 11100, 11011, 10010, 10101.
This as every polynomial cod, is indeed a linear code, i.e. linear combinations of code words are again code words. In case like this where the field is GF(2), linear Combinations are found by taking the X or the code words expressed in binary form (e.g.00111 XOR 10010=10101)
Example 3: (Theorem): The matrix ideals of the ring Z of integers are the principal ideals generated by prime integers.
Proof: Every ideal of Z is principal. Consider a principal ideal (n), with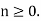 If n is a prime , say n=p , then
If n is a prime , say n=p , then 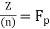 , a field , the ideal (n) is maximal , If n is not prime , there are three possibilities : n=0, n=1 , or n factors . Neither the zero ideal nor the unit ideal is maximal. If n factors, say n=ab, with 1<a<n, then 1
, a field , the ideal (n) is maximal , If n is not prime , there are three possibilities : n=0, n=1 , or n factors . Neither the zero ideal nor the unit ideal is maximal. If n factors, say n=ab, with 1<a<n, then 1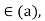 therefore (n)<(a)<(1). The ideal (n) is not maximal.
therefore (n)<(a)<(1). The ideal (n) is not maximal.
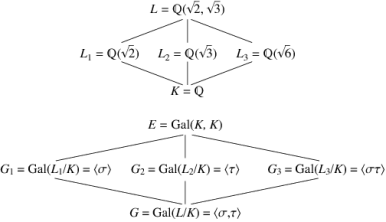
Galois Theory: In mathematics, Galois theory provides a connection between field theory and group theory. Using Galois theory, certain problems in field theory can be reduced to group theory, which is in some sense simpler and better understood. It has been used to solve classic problems including showing that two problems of antiquity cannot be solved as they were stated (doubling the cube and trisecting the angle); showing that there is no quintic formula; and showing which polygons are constructible.
The subject is named after Evariste Galois, who introduced it for studying the roots of a polynomial and characterizing the polynomial equations that are solvable by radicals in terms of properties of the permutation group of their roots—an equation is solvable by radicals if its roots may be expressed by a formula involving only integers, nth roots, and the four basic arithmetic operations.
The theory has been popularized among mathematicians and developed by Richard Dedekind, Leopold Kronecker, Emil Artin, and others who interpreted the permutation group of the roots as the automorphism group of a field extension.
Galois Theory has been generalized to Galois connections and Grothendieck's Galois Theory.
Fundamental theorem of Galois Theory:
Statement: For a Galois extension field K of field F, the fundamental theorem of Galois theory sates that the subgroups, of the Galois group G = Gal(K/F) correspond with the sub-field K containing F.If the sub-field L corresponds to subgroup H, then the extension field degree K over L is the group order of H.
Proof:
Given 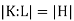
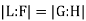
Suppose 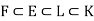 , then E and L corresponds to subgroups HE and HL of G such that HE is a subgroup of HL .Also HE is a normal subgroup if E is a Galois extension field.Since any subfield of a separable extension, which the Galois extension field K must be separable.
, then E and L corresponds to subgroups HE and HL of G such that HE is a subgroup of HL .Also HE is a normal subgroup if E is a Galois extension field.Since any subfield of a separable extension, which the Galois extension field K must be separable.
Then E is Galois if E is a normal extension of F.So normal extensions correspond to normal subgroups.When HE is normal then,
Gal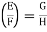
As the quotient group of the group action of G on K.
Example1: Let E = Q(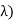 be the field of rational functions in
be the field of rational functions in 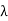 and let
and let
G = 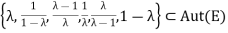
Which is a group under composition, isomorphic to S3?
Solution: Let F be the fixed field of g, then
Gal(E/F) = G
If H is a sub group of G then co-efficient of the following polynomial are given by
P(T) = 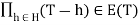
Generate the fixed field H.
Galois correspondence means that every subfield of E/F can be constructed this way.
Example if H= 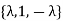 then the fixed field is Q(
then the fixed field is Q(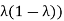 and if H =
and if H = 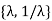 then the fixed field is Q(
then the fixed field is Q(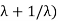 .
.
Likewise one can write F, the fixed field of G as Q(j) where j is j-invariant.
Group Theory: Inmathematics and abstract algebra, group theory studies the algebraic structures known as groups. The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces, can all be seen as groups endowed with additional operations and axioms. Groups recur throughout mathematics, and the methods of group theory have influenced many parts of algebra. Linear algebraic groups and Lie groups are two branches of group theory that have experienced advances and have become subject areas in their own right.
Various physical systems, such as crystals and the hydrogen atom, may be modeled by symmetry groups. Thus group theory and the closely related representation theory have many important applications in physics, chemistry, and materials science. Group theory is also central to public key cryptography.
The early history of group theory dates from the 19th century. One of the most important mathematical achievements of the 20th century was the collaborative effort, taking up more than 10,000 journal pages and mostly published between 1960 and 1980, that culminated in a complete classification of finite simple groups.
Field Theory: In algebra, there are several important algebraic structures, one of which is called a field. Before getting into the formal definition of a field, let's start by thinking of a field as a set of things, or 'elements' (not necessarily numbers) which can be 'added' and 'multiplied'. Remember that we are not referring to the addition and multiplication that you may be used to from arithmetic, but rather any two operations that are defined for each field. Also, in order for the set with two operations to be called a field, a series of field axioms must be met. Those will be explained in the formal definition of a field that follows.
So, to formally define a field we will use the notation (F, +, *) to represent the field with set F and operations + (addition) and * (multiplication). As we mentioned above, the operations + and * must meet the following field axioms:
1. Closure under addition and multiplication: For all a andb in F, both a + b and a * b are in F. (In other words, any two elements from the set that are added or multiplied should also result in an element of that set.)
2. Addition and multiplication must be associative: (Note that this is the same associative property that you may be familiar with from arithmetic.)
For all a, b, and c in F we must have:
a + (b + c) = (a + b) + c
and
a * (b * c) = (a * b) * c
3. Addition and multiplication must be commutative: (Note that this is the same commutative property that you may be familiar with from arithmetic.)
For all a andb in F, the following are true:
a + b = b + a
and
a * b = b * a
4. Existence of additive and multiplicative identity elements: There exists an element of F, denoted 0, such that for all a in F, a + 0 = a. Similarly, there exists an element of F, denoted 1, such that for all a in F, a * 1 = a.
5. Existence of additive and multiplicative inverse elements: For every element a in F, there exists an element of F, denoted -a, such that a + -a = 0. Similarly, for every non-zero element a in F, there exists an element of F, denoted a-1, such that a * a-1 = 1.
6. Multiplication is distributive over addition: For all a, b, and c in F, the following is true:
a * (b + c) = (a * b) + (a * c)