3.1 Searching | unit 3 searching and sorting

FDS

Unit 3

Searching and Sorting

3.1 Searching

1. Linear /Sequential search

Linear search is the simplest searching algorithm that searches for an element in a list in sequential order. We start at one end and check every element until the desired element is not found.

Algorithm

Linear Search (Array A, Value x)

Step 1: Set i to 1

Step 2: if i> n then go to step 7

Step 3: if A[i] = x, then go to step 6

Step 4: Set i to i + 1

Step 5: Go to Step 2

Step 6: Print Element x Found at index i and go to step 8

Step 7: Print element not found

Step 8: Exit

Array to be search for

Start from element k with element x

K=1

K≠2

K≠4

K≠0

2. If x==k then return index

K=1

3. Else return ; element not found

Time complexity of linear search O(n)

Space complexity of linear search O(1)

Where n is no. of elements

3.2 Sentinel search

Sentinel search is a type of Linear Search where the numbers of comparisons are reduced as compared to a traditional linear search.

When a linear search is performed on an array of size N then in the worst case a total of N comparisons are made when the element to be searched is compared to all the elements of the array and (N + 1) comparisons are made for the index of the element to be compared so that the index is inside bounds of the array which can be reduced in a Sentinel Linear Search.

In this search, the last element of the array is replaced with the element to be searched and then the linear search is performed on the array without checking whether the current index is inside the index range of the array or not because the element to be searched will definitely be found inside the array

If the element was not present in the original array since the last element got replaced with it. So, the index to be checked will never be out of bounds of the array.

The number of comparisons in the worst case here will be (N + 2).

E.g. Input: arr[] = {10, 20, 180, 30, 60, 50, 110, 100, 70}, x = 180

180

110

100

index 0 1 2 3 4 5 6 7 8

Output: 180 is present at index 2

Input: arr[] = {10, 20, 180, 30, 60, 50, 110, 100, 70}, x = 90

180

110

100

index 0 1 2 3 4 5 6 7 8

Output: element not found

Time complexity of linear search O(n)

Space complexity of linear search O(1)

Where n is no. of elements

3.3 Binary search

Binary Search is a searching algorithm for finding an element's position in a sorted array.

A binary search algorithm is a technique for finding particular value in a linear array, by ruling out half of the data at each step.

A binary search finds the median, makes comparisons’ to determine whether the desired value comes before or after it, then searches the remaining half in the same manner.

Algorithm

Function Binary search(a, value, left ,right)

If right<left

Return not found

Mid= floor((right-left)/2)+ left;

If a[mid]=value

Return mid

If value<a[mid]

Return binarysearch(a,value,left,mid-1)

Else

Return binarysearch(a,value,mid+1,right)

1. The array in which searching is to be performed is

Element to find x=4

2. Set two pointers low and high at the lowest and the highest positions respectively

Low high

3. Find the middle element mid=arr(low+high)/2= 6

Mid

4.If x == mid, then return mid. Else, compare the element to be searched with m.

5. If x > mid, compare x with the middle element of the elements on the right side of mid. This is done by setting low to low = mid + 1.

6. Else, compare x with the middle element of the elements on the left side of mid. This is done by setting high to high = mid - 1.

Low high

7. Repeat steps 3 to 6 until low meets high.

Low mid high

8 if x==mid return

X=mid

Binary search complexities

Time Complexities

Best case complexity: O(1)

Average case complexity: O(log n)

Worst case complexity: O(log n)

Space Complexity

The space complexity of the binary search is O(n).

3.4 Fibonacci search

Fibonacci Search is a comparison-based technique that uses Fibonacci numbers to search an element in a sorted array.

Similarities with Binary Search:

Works for sorted arrays

A Divide and Conquer Algorithm.

Has Log n time complexity.

Differences with Binary Search:

Fibonacci Search divides given array in unequal parts

Binary Search uses division operator to divide range.

Fibonacci Searchuses ‘+’ and’–‘ and doesn’t use ‘/’ The division operator could also be costly on some CPUs.

Fibonacci Search examines relatively closer elements in subsequent steps. So when input array is big that can't slot in CPU cache or maybe in RAM,

Fibonacci Search are often useful.

Fibonacci Numbers are recursively defined as F(n) = F(n-1) + F(n-2), F(0) = 0, F(1) = 1.

First few Fibonacci Numbers are 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …

Algorithm

Let the searched element be x.

The idea is to first find the littlest Fibonacci number that's greater than or adequate to the length of given array. Let the found Fibonacci number be fib (m’th Fibonacci number).

We use (m-2)’th Fibonacci number because the index (If it's a legitimate index).

Let (m-2)’th Fibonacci number be i, we compare arr[i] with x, if x is same, we return i.

Else if x is bigger, we recur for sub array after i, else we recur for sub array before i.

Below is that the complete algorithm

Let arr[0..n-1] be the input array and element to be searched be x.

Find the littlest Fibonacci number greater than or adequate to n. Let this number be fibM [m’th Fibonacci number]. Let the 2 Fibonacci numbers preceding it's fibMm1 [(m-1)’th Fibonacci Number] and fibMm2 [(m-2)’th Fibonacci Number].

While the array has elements to be inspected:

Compare x with the last element of the range covered by fibMm2
If x matches, return index
Else if x is a smaller amount than the element, move the three Fibonacci variables two Fibonacci down, indicating elimination of roughly rear two-third of the remaining array.
Else x is bigger than the element, move the three Fibonacci variables one Fibonacci down. Reset offset to index. Together these indicate elimination of roughly front one-third of the remaining array.

Since there could be one element remaining for comparison, check if fibMm1 is 1. If yes, compare x thereupon remaining element. If match, return index.

Time complexity for Fibonacci search

The worst case will occur once we have our target within the larger (2/3) fraction of the array, as we proceed to seek out it. In other words, we are eliminating the smaller (1/3) fraction of the array whenever. We call once for n, then for(2/3) n, then for (4/9) n and henceforth.

Time complexity=O(log n)

3.5 Indexed sequential search

In this searching method, first of all, an index file is made, that contains some specific group or division of required record when the index is obtained, then the partial indexing takes less time cause it's located during a specified group.

When the user makes an invitation for specific records it'll find that index group first where that specific record is recorded.

Characteristics of Indexed Sequential Search:

In Indexed Sequential Search a sorted index is about aside additionally to the array.

Each element within the index points to a block of elements within the array or another expanded index.

The index is searched 1st then the array and guides the search within the array.

Indexed Sequential Search actually does the indexing multiple time, like creating the index of an index.

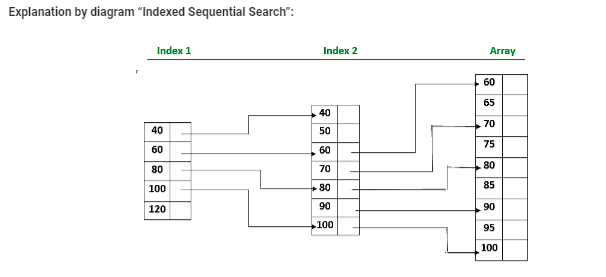
$C:\Users\Kilua Zoldyck\Pictures\ss.png$

Time complexity of indexed sequential search

best case complexity is O(1)

worst case complexity is O(n)

Space complexity O(1)

3.6 Types of Sorting-Internal and External Sorting

There are two different categories in sorting:

Internal sorting

External sorting

Internal sorting:

If the input file is such it are often adjusted within the main memory directly, it's called internal sorting.

internal sorting stores the info to be sorted within the memory itself all the time when the sorting is ongoing

It is usually applied in cases where data can't be fit into the memory.

In internal sorting you'll randomly access elements from the memory while in external accessing data from the disks will take a while

Internal sorting are sort of sorting which is employed when the whole collection of knowledge is little enough that sorting can happen within main memory.

There’s no need for external memory for execution of sort program.

It is used when size of input is little

In internal sorting the info that has got to be sorted are going to be within the main memory always, implying faster access. Complete sorting will happen in main memory. Insertion sort, quick sort, heap sort, radix sort are often used for internal sorting

Examples:- Bubble sort, insertion sort,quicksort, heapsort

The sorting during which there's no got to use another storage structure because the data is manageable enough within the RAM.

External sorting:

If the input file is such it can't be adjusted within the memory entirely directly, it must be stored during a hard disc,diskette, or the other memory device. This is often called external sorting.

.In external sorting it'll on disks, outside main memory. It are often because the info is large and can't be stored in main memory. While sorting the info will pulled over in chunks from disk to main memory.

Later all the sorted data are going to be merged and stored back to disk, where it can fit. External merge sort are often used here.

External sorting may be a term for a category of sorting algorithms which will handle massive amounts of knowledge.

External sorting is required when the info being sorted don't fit into the most memory of a computer (usually RAM) and instead, they need to reside within the slower external memory (usually a tough drive).

External sorting typically uses a hybrid sort-merge strategy. Within the sorting phase, chunks of knowledge sufficiently small to suit in main memory are read, sorted, and written bent a short lived file. Within the merge phase, the sorted sub-files are combined into one larger file.

But in external sorting data is loaded into the memory only it's required.

One example of external sorting is that the external merge sort algorithm, which sorts chunks that every slot in RAM, then merges the sorted chunks together.

We first divide the file into runs such the dimensions of a run is little enough to suit into main memory. Then sort each run in main memory using merge sort algorithm. Finally merge the resulting runs together into successively bigger runs, until the file is sorted.

3.7 General Sort Concepts-Sort Order, Stability, Efficiency, and Number of Passes

General Sort Order

For any column, sorting is performed in the following order:

Sorting based on data type

Mismatched values

Null/empty values

Sort Order for StringsSince all values are valid for String data type, this sort order represents the most common representation for sort order.

Sorting based on data type:

a) Numeric values (low value to high value)

b) Whitespace

c) Special characters

d) Alphabetical

Case-insensitive

Accented characters (ä) are below unaccented character (a)

Mismatched values

Null/empty values

Sort Order for Integers and Decimals

For Integers and Decimals, sorting happens in the following order:

Sorting based on data type:

Numeric values (low value to high value)

Mismatched values

Null/empty values

Stability

Stability is especially important once we have key-value pairs with duplicate keys possible (like people names as keys and their details as values). And that we wish to sort these objects by keys.

An algorithm is claimed to be stable if two objects with equal keys appear within the same order in sorted output as they seem within the input array to be sorted.

Most sorting algorithms work by comparing the info being sorted. In some cases, it's going to be desirable to sort an outsized chunk of knowledge (for instance, a struct containing a reputation and address) supported only some of that data. The piece of knowledge actually won’t to determine the sorted order is named the key.

Efficiency

Sorting algorithms are usually judged by their efficiency. During this case, efficiency refers to the algorithmic efficiency because the size of the input grows large and is usually supported the number of elements to sort. Most of the algorithms in use have an algorithmic efficiency of either O(n^2) or O(n*log(n)).

A couple of special case algorithms (one example is mentioned in Programming Pearls) can sort certain data sets faster than O(n*log(n)). These algorithms aren't supported by comparing the things being sorted and believe tricks. It’s been shown that no key-comparison algorithm can perform better than O(n*log(n)).

Many algorithms that have an equivalent efficiency don't have an equivalent speed on an equivalent input. First, algorithms must be judged supported their average case, best case, and worst-case efficiency. Some algorithms, like quicksort, perform exceptionally well for a few inputs, but horribly for others. Other algorithms, like merge sort, are unaffected by the order of input file.

Even a modified version of bubble sort can finish in O(n) for the foremost favorable inputs.

A good algorithm is correct, but an excellent algorithm is both correct and efficient. The foremost efficient algorithm is one that takes the smallest amount of execution time and memory usage possible while still yielding an accurate answer.

Number of passes

Number of passes in an algorithm is basically the count of iterations that will take to get the desired output

searchList([3, 37, 45, 57, 93, 120], 45)

The algorithm starts off by initializing the variable index to 1. It then begins to loop.

Iteration #1:

It checks if the index is bigger than LENGTH(numbers). Since 1 isn't greater than 6, it executes the code inside the loop.

It compares numbers[index] to target number. Since 3 isn't adequate to 45, it doesn't execute the code inside the conditional.

It increments index by 1, so it now stores 2.

Iteration #2:

It checks if the index is bigger than LENGTH(numbers). Since 2 isn't greater than 6, it executes the code inside the loop.

It compares numbers[index] to target number. Since 37 isn't adequate to 45, it doesn't execute the code inside the conditional.

It increments index by 1, so it now stores 3.

Iteration #3:

It checks if the index is bigger than LENGTH(numbers). Since 3 isn't greater than 6, it executes the code inside the loop.

It compares numbers[index] to target number. Since 45 is adequate to 45, it executes the code inside the conditional.

It returns the present index, 3.

Now let's count the number of operations that the linear search algorithm needed to seek out that value, by counting how often each sort of operation was called.

Operation	No of times
Initialize index to 1	1
Check if the index is bigger than LENGTH(numbers)	3
Check if numbers[index] equals targetNumber	3
Return index	1
Increment index by 1	2

That's a complete of 10 operations to seek out the target number at the index of three. Notice the connection to the amount 3? The loop repeated 3 times, and every time, it executed 3 operations.

3.8 Comparison Based Sorting Methods-Bubble Sort, Insertion Sort, Selection Sort, Quick Sort, Shell Sort

1. Bubble sort

Bubble sort is an algorithm that compares the adjacent elements and swaps their positions if they are not in the intended order. The order can be ascending or descending

Algorithm

bubbleSort(array)

for i<- 1 to indexOfLastUnsortedElement-1
if leftElement>rightElement
swap leftElement and rightElement

end bubbleSort

Starting from the first index, compare the first and the second elements. If the first element is greater than the second element, they are swapped. Now, compare the second and the third elements. Swap them if they are not in order. The above process goes on until the last element

$C:\Users\Kilua Zoldyck\Pictures\b1.png$

2. The same process goes on for the remaining iterations. After each iteration, the largest element among the unsorted elements is placed at the end. In each iteration, the comparison takes place up to the last unsorted element.

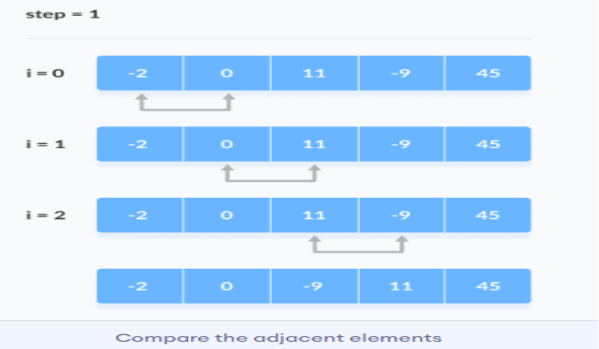
$C:\Users\Kilua Zoldyck\Pictures\b2.png$

3. The same process goes on for the remaining iterations. After each iteration, the largest element among the unsorted elements is placed at the end. In each iteration, the comparison takes place up to the last unsorted element.

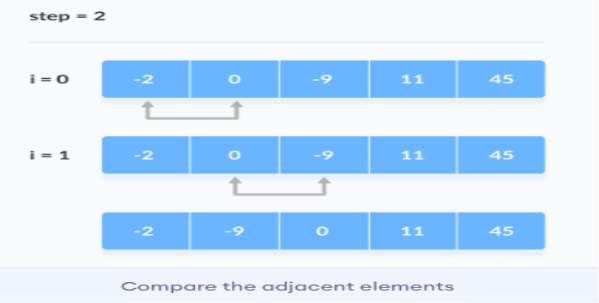
$C:\Users\Kilua Zoldyck\Pictures\b3.png$

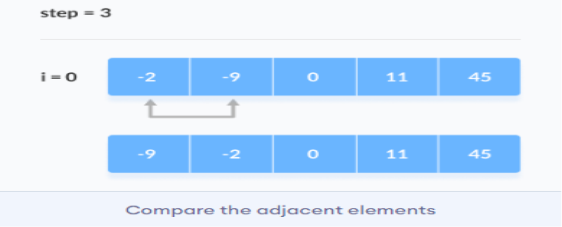
The array is sorted when all the unsorted elements are placed at their correct positions.

$C:\Users\Kilua Zoldyck\Pictures\b4.png$

Time Complexities:

Worst Case Complexity:O(n2)

Best Case Complexity:O(n)

Average Case Complexity:O(n2)

Space Complexity:

Space complexity is O(1) because an extra variable temp is used for swapping.

Bubble Sort Applications

Bubble sort is used in the following cases where

The complexity of the code does not matter.

A short code is preferred.

2. Insertion sort

Insertion sort is a comparison sort in which the sorted array is built one entry at a time.

It is less efficient on large lists than more advanced algorithms such as quick sort ,heap sort or merge sort

This algorithm does not require extra memory

For insertion sort the worst case running time is O(n^2) and best case running time is O(n).

Insertion sort use no extra memory it sort in place.

The time of insertion sort is depends on the original order of input.

Algorithm

insertionSort(array)

mark first element as sorted

for each unsorted element X

'extract' the element X

for j <- lastSortedIndex down to 0

if current element j > X

move sorted element to the right by 1

break loop and insert X here

end insertionSort

1. The first element in the array is assumed to be sorted. Take the second element and store it separately in key.

Array

$C:\Users\Kilua Zoldyck\Pictures\a1.png$

Compare key with the first element. If the first element is greater than key, then key is placed in front of the first element.

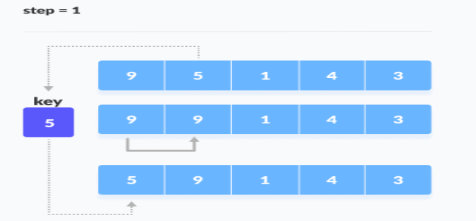
$C:\Users\Kilua Zoldyck\Pictures\a2.png$

If the first element is greater than key, then key is placed in front of the first element

2. Now, the first two elements are sorted.Take the third element and compare it with the elements on the left of it. Placed it just behind the element smaller than it. If there is no element smaller than it, then place it at the beginning of the array.

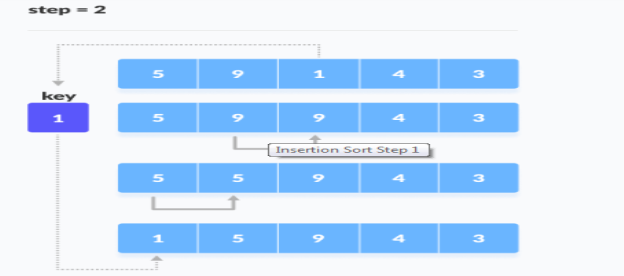
$C:\Users\Kilua Zoldyck\Pictures\a3.png$

Place 1 at the beginning

3. Similarly, place every unsorted element at its correct position.

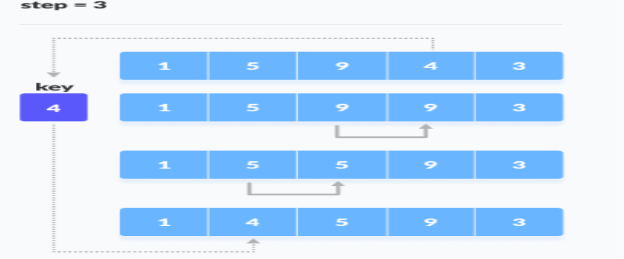
$C:\Users\Kilua Zoldyck\Pictures\a5.png$

Place 4 behind 1

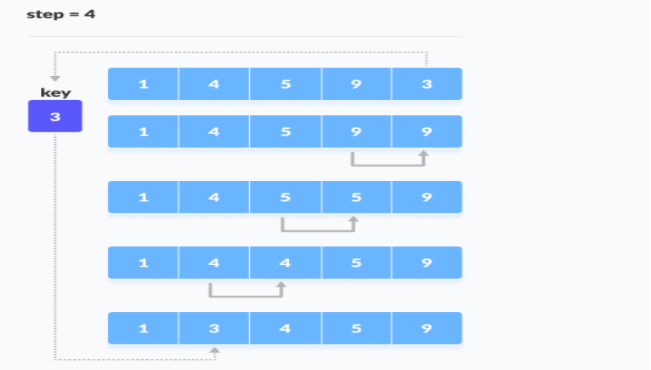
$C:\Users\Kilua Zoldyck\Pictures\a6.png$

Place 3 behind 1 and the array is sorted

3. Selection sort

Selection sort is a sorting algorithm specifically an in place comparision sort.

It has O(n) complexity making it efficient on large lists

Implementation

Find the minimum value in the list

Swap it with the value in first position

Repeat the steps above for the rest of the list(starting at second and advance each time.

Algorithm

For i← 1 to n-1 do

Min j ←I;

Min x← A[i]

For j← i+1

If A[j] <min x then

Min j← j

Min x ←A[j]

A[i] ←min x

Set the first element as minimum. Select

Selection Sort Steps

First element as minimum

2. Compare minimum with the second element. If the second element is smaller than minimum, assign the second element as minimum.
Compare minimum with the third element. Again, if the third element is smaller, then assign minimum to the third element otherwise do nothing. The process goes on until the last element.

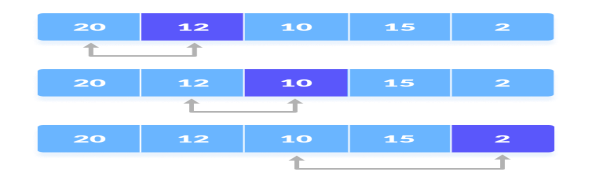Selection Sort Steps Compare minimum with the remaining elements

3. After each iteration, minimum is placed in the front of the unsorted list. Selection Sort Steps

Swap the first with minimum

4. For each iteration, indexing starts from the first unsorted element. Step 1 to 3 are repeated until all the elements are placed at their correct positions.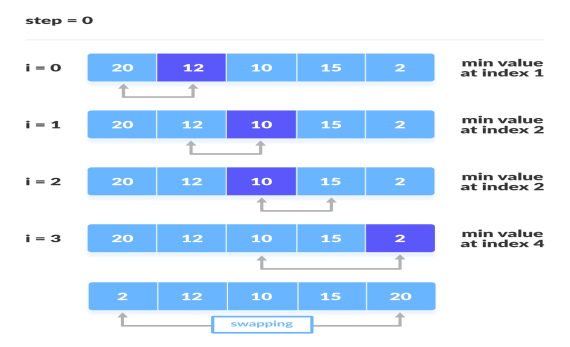 Selection Sort Steps

The first iteration

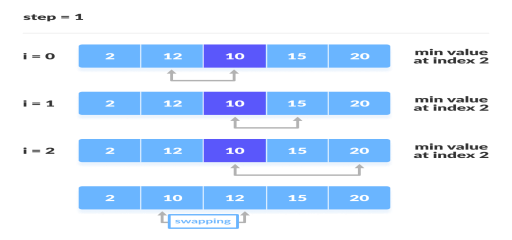
Selection sort steps

The second iteration

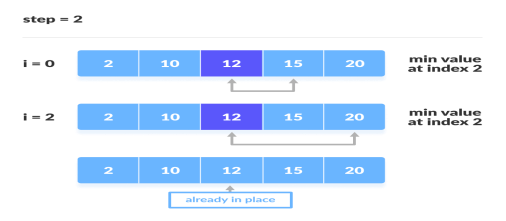
Selection sort steps

The third iteration

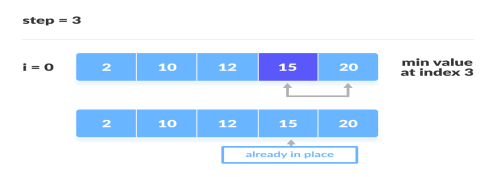
Selection sort steps

The fourth iteration

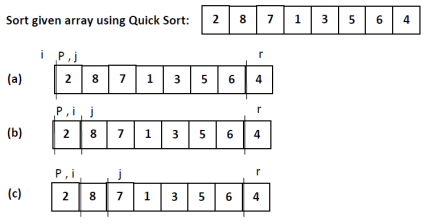
4. Quick sort

Algorithm

quickSort(array, leftmostIndex, rightmostIndex)

if (leftmostIndex<rightmostIndex)
pivotIndex<- partition(array,leftmostIndex, rightmostIndex)
quickSort(array, leftmostIndex, pivotIndex)
quickSort(array, pivotIndex + 1, rightmostIndex)

partition(array, leftmostIndex, rightmostIndex)

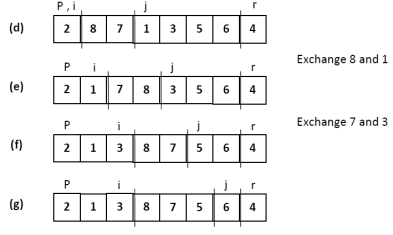
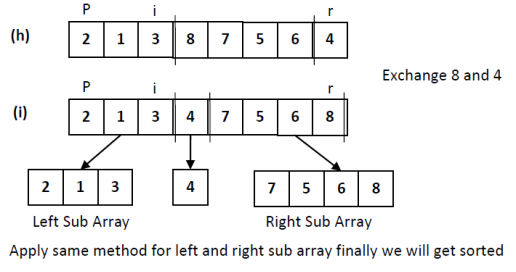
set rightmostIndex as pivotIndex
storeIndex<- leftmostIndex – 1
for i<- leftmostIndex + 1 to rightmostIndex
if element[i] <pivotElement
swap element[i] and element[storeIndex]
storeIndex++
swap pivotElement and element[storeIndex+1]
return storeIndex + 1

Quick sort

Quicksort is that the currently fastest known algorithm and is usually the simplest practical choice for sorting,as its average expected time period is O(n log(n)).

Pick a component, called a pivot, from the array.

Reorder the array in order that all elements with values but the pivot precede the pivot, while allelements with values greater than the pivot come after it (equal values can go either way). After thispartitioning, the pivot is in its final position. This is often called the partition operation.

Recursively apply the above steps to the sub-array of elements with smaller values and separately to thesub-array of elements with greater values.

Quicksort, like merge sort, may be a divide-and-conquer recursive algorithm.

The basic divide-and-conquer process for sorting a sub array A[i..j] is summarized within the following three easysteps:

Divide: Partition T[i..j] Into two sub arrays T[i..l-1] and T[l+1… j] such each element of T[i..l-1] isless than or adequate to T[l], which is, in turn, but or adequate to each element of T[l+1… j]. Compute theindex l as a part of this partitioning procedure
Conquer: Sort the 2 sub arrays T[i..l-1] and T[l+1… j] by recursive calls to quicksort.
Combine: Since the sub arrays are sorted in situ, no work is required to combing them: the whole arrayT[i..j], is now sorted.

$C:\Users\Kilua Zoldyck\Pictures\q1.png$

$C:\Users\Kilua Zoldyck\Pictures\q2.png$

$C:\Users\Kilua Zoldyck\Pictures\q3.png$

5. Shell sort

Algorithm

ShellSort(array, size)

for interval i<- size/2n down to 1
for each interval "i" in array
sort all the elements at interval "

end shellSort

1. Suppose, we need to sort the following array.

Initial array

Shell sort step

2. We are using the shell's original sequence (N/2, N/4, ...1) as intervals in our algorithm

In the first loop, if the array size is N = 8 then, the elements lying at the interval of N/2 = 4 are compared and swapped if they are not in order.

The 0th element is compared with the 4th element.

If the 0th element is greater than the 4th one then, the 4th element is first stored in temp variable and the 0th element (ie. greater element) is stored in the 4th position and the element stored in temp is stored in the 0th position.

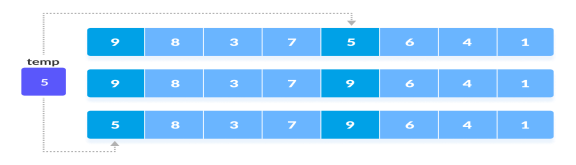
Shell Sort step

Rearrange the elements at n/2 interval

This process goes on for all the remaining elements.

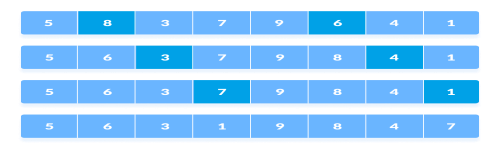
Shell Sort steps

Rearrange all the elements at n/2 interval

3. In the second loop, an interval of N/4 = 8/4 = 2 is taken and again the elements lying at these intervals are sorted

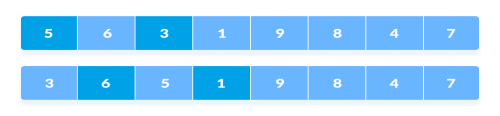
Shell Sort step

Rearrange the elements at n/4 interval

Shell Sort step

All the elements in the array lying at the current interval are compared. The elements at 4th and 2nd position are compared. The elements at 2nd and 0th position are also compared. All the elements in the array lying at the current interval are compared.

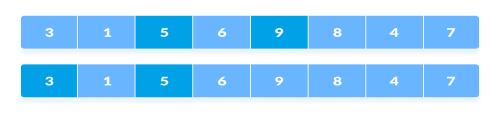
4. The same process goes on for remaining elements.

Shell Sort step

Rearrange all the elements at n/4 interval

5. Finally, when the interval is N/8 = 8/8 =1 then the array elements lying at the interval of 1 are sorted. The array is now completely sorted.

Shell Sort step

Rearrange the elements at n/8 interval

3.9 Non-comparison Based Sorting Methods-Radix Sort, Counting Sort, and Bucket Sort

1. Radix Sort

Algorithm

radixSort(array)

d <- maximum number of digits in the largest element
create d buckets of size 0-9
for i<- 0 to d
sort the elements according to ith place digits using countingSort

countingSort(array, d)

max <- find largest element among dth place elements
initialize count array with all zero
for j <- 0 to size
find the total count of each unique digit in dth place of elements and
store the count at jth index in count array
for i<- 1 to max
find the cumulative sum and store it in count array itself
for j <- size down to 1
restore the elements to array
decrease count of each element restored by 1

input array=[576, 494, 194,296,278,176, 954}

input

576 49[4] 9[5]4 [1]76 176

494 19[4] 5[7]6 [1]94 194

194 95[4] 1[7]6 [2]78 278

296 → 57[6] → 2[7]8 → [2]96→ 296

278 29[6] 4[9]4 [4]94 494

176 17[6] 1[9]4 [5]76 576

954 27[8] 2[9]6 [9]54 954

2. Counting Sort

Counting sort assumes that each of the n inputs elements is an integer in the range 0 to k for some integer k. When k=O(n) time the sort runs in O(n) time.

The basic idea of counting sort is to determine for each input element x the number of elements less than x.

This information can be used to place elements x directly into its position in the output array

Algorithm

COUNTING-SORT(A,B,K)

For I← 0 to k

Do C[i]←0

For j←1 to length[A]

Do C[A[j]]← C[A[j]]+1

/* C[i] now contains the number of elements equal to i. */

For i← 1 to k

C[i] ← C[i] + C[i-1]

/* C[i] now contains the number of elements less than or equal to i. */

For j← length[A] down to 1

Do B[C[A[j]]] ←A[j]

C[A[j]] ←C[A[j]]-1

An important property of counting sort is that it is stable; numbers with the same value appear in the output array in the same order as they do in the input array

That is ties between two numbers are broken by the rule that whichever number appears first in the input array appears first in the output array.

Normally the property of stability is important only when satellite data are carried around with the element being sorted.

Find out the maximum element (let it be max) from the given array.

$C:\Users\Kilua Zoldyck\Pictures\cs1.png$

2. Initialize an array of length max+1 with all elements 0. This array is used for storing the count of the elements in the array.

$C:\Users\Kilua Zoldyck\Pictures\cs2.png$

3. Store the count of each element at their respective index in count array.

For example: if the count of element 3 is 2 then, 2 is stored in the 3rd position of count array. If element "5" is not present in the array, then 0 is stored in 5th position.

$C:\Users\Kilua Zoldyck\Pictures\cs3.png$

4. Store cumulative sum of the elements of the count array. It helps in placing the elements into the correct index of the sorted array.

$C:\Users\Kilua Zoldyck\Pictures\cs4.png$

5. Find the index of each element of the original array in the count array. This gives the cumulative count. Place the element at the index calculated as shown in figure below.

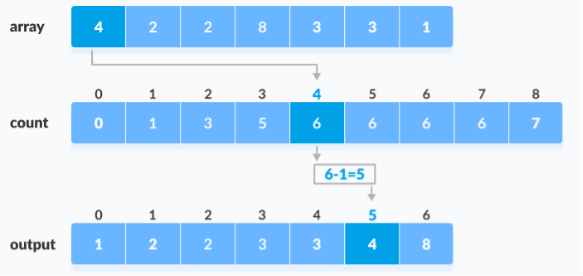
$C:\Users\Kilua Zoldyck\Pictures\cs5.png$

6. After placing each element at its correct position, decrease its count by on

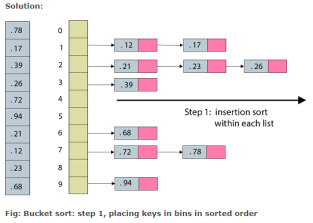
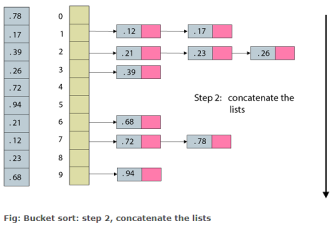
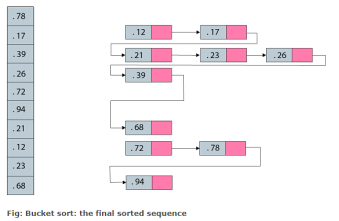
3. Bucket Sort

Algorithm

bucketSort()

create N buckets each of which can hold a range of values
for all the buckets
initialize each bucket with 0 values
for all the buckets
put elements into buckets matching the range
for all the buckets
sort elements in each bucket
gather elements from each bucket

end bucketSort

bucket sort

arrayA = (0.78, 0.17, 0.39, 0.26, 0.72, 0.94, 0.21, 0.12, 0.23, 068)

$C:\Users\Kilua Zoldyck\Pictures\bn1.png$ $C:\Users\Kilua Zoldyck\Pictures\b2.png$

$C:\Users\Kilua Zoldyck\Pictures\b3.png$

3.10 Comparison of All Sorting Methods and their complexities.

S no.	Sorting algorithm	Time complexity			Space complexity
S no.	Sorting algorithm	Best case	Average case	Worst case	Space complexity
1	Bubble sort	O(n)	O(n^2)	O(n^2)	O(1)
2	Selection sort	O(n^2)	O(n^2)	O(n^2)	O(1)
3	Insertion sort	O(n)	O(n^2)	O(n^2)	O(1)
4	Quick sort	O(n log n)	O(n log n)	O(n^2)	O(n)
5	Merge sort	O(n log n)	O(n log n)	O(n log n)	O(n)
6	Heap sort	O(n log n)	O(n log n)	O(n log n)	O(1)
7	Radix sort	O (nk)	O(nk)	O(nk)	O(n+k)
8	Counting sort	O (n+k)	O(n+k)	O(n+k)	O(k)
9	Bucket sort	O (n+k)	O(n+k)	O(n^2)	O(n)

Sign Up

Index

Notes

Highlighted

Underlined

Browse by Topics

Notes

Highlighted

Underlined