Unit 4
Linked List
Memory Allocation
- Compile-time or Static Memory Allocation
- Run-time or Dynamic Memory Allocation
Static Memory Allocation
Dynamic Memory Allocation
Difference between Static and Dynamic Memory Allocation
S. no | Static memory allocation | Dynamic memory allocation |
1 | In the static memory allocation, variables get allocated permanently. | I n the Dynamic memory allocation, variables get allocated as long as your program unit gets active. |
2 | Static Memory Allocation is completed before program execution. | Dynamics Memory Allocation is completed during program execution.
|
3 | It uses stack for managing the static allocation of memory. | It uses heap for managing the dynamic allocation of memory. |
4 | It is less efficient. | It is more efficient. |
5 | In Static Memory Allocation, there's no memory re-usability. | In Dynamics Memory Allocation, there's memory re-usability and memory are often freed when not required. |
6 | In static memory allocation, once the memory is allocated, the memory size can't change. | In dynamic memory allocation, when memory is allocated the memory size are often changed.
|
7 | During this memory allocation scheme, we cannot reuse the unused memory. this enables reusing the memory. | The user can allocate more memory when required. Also, the user can release the memory when the user needs it. |
8 | In this memory allocation scheme, execution is faster than dynamic memory allocation | In this memory allocation scheme, execution is slower than static memory allocation. |
9 | In this memory is allocated at compile time | During this memory is allocated at run time. |
10 | In this allocated memory remains from start to finish of the program | During this allocated memory are often released at any time during the program. |
11 | Example: This static memory allocation is usually used for array | Example: This dynamic memory allocation is usually used for linked list. |
Linear arrangement and their linked storage representation.
There are many applications where sequential allocation method is unacceptable due to following characteristics:-
The linked allocation method of storage may result in both efficient use of memory and computer time.
Linked List
Operations on linked list
1. Singly Linked List

2. Circular Linked List

3. Doubly Linked list

4. Doubly circular link list

Advantages of Linked List
Disadvantages of Linked List
1. Singly linked list
1. Insertion at start first position
Function: INSERT(X, First )
IF AVAIL = NULL
Then Write (“Availability Stack Underflow”)
Return(FIRST)
AVAIL←NEW
LINK(AVAIL)←AVAIL
X←INFO (NEW)
FIRST←LINK (NEW)
Return (NEW)
When INSERT is invoked it returns a pointer value to the variable FIRST
INSERT (X, FIRST)←FIRST
2. Insertion at end
Function: INSEND(X, First) (Insert at end)
INFO and LINK fields.
variable.
IF AVAIL = NULL
Then Write (“Availability Stack Underflow”)
Return(FIRST)
AVAIL←NEW
LINK(AVAIL)←AVAIL
X←INFO (NEW)
NULL←LINK (NEW)
If FIRST = NULL
then Return (NEW)
FIRST←SAVE
Repeat while LINK (SAVE) ≠ NULL
LINK (SAVE)←SAVE
NEW←LINK (SAVE)
Return (FIRST)
When INSERTEND is invoked it returns a pointer value to the variable FIRST
INSERTEND (X, FIRST)←FIRST
3. Insert a node into Ordered Linked List
- Remove a node from availability stack.
- Set the sector of latest node.
- If the linked list is empty then return the address of latest node.
- If node precedes all other nodes within the list then inserts a node at the front of the list and returns itsaddress.
- Repeat step 6 while information contain of the node within the list is a smaller amount than the knowledge content of the new node.
- Obtain subsequent node within the linked list.
- Insert the new node within the list and address of its first node.
Function: INSORD(X, FIRST)
INFO and LINK fields.
IF AVAIL = NULL
Then Write (“Availability Stack Underflow”)
Return(FIRST)
AVAIL←NEW
LINK(AVAIL)←AVAIL
If FIRST = NULL
NULL←then LINK (NEW)
Return (NEW)
If INFO(NEW) ≤ INFO (FIRST)
FIRST←then LINK (NEW)
Return (NEW)
FIRST←SAVE
Repeat while LINK (SAVE) ≠ NULL and INFO (NEW) ≥ INFO (LINK (SAVE))
LINK (SAVE)←SAVE
LINK (SAVE)←LINK (NEW)
NEW←LINK (SAVE)
Return (FIRST)
When INSERTORD is invoked it returns a pointer value to the variable FIRST
INSERTORD (X, FIRST)←FIRST
4. Deletion a node from Linked List
Function: DELETE(X, FIRST)
If FIRST = NULL
then write (‘Underflow’)
return
FIRST←SAVE
Repeat thru step-5 while SAVE ≠ X and LINK (SAVE) ≠ NULL
SAVE←PRED
LINK (SAVE)←SAVE
If SAVE ≠ X
then write (‘Node not found’)
return
If X = FIRST (if X is first node?)
LINK (FIRST)←then FIRST
LINK (X)←else LINK (PRED)
Free (X)
Function: COPY (FIRST)
- If the list is empty then return null
- If the supply stack is empty then write availability stack underflow and return else copy the primarynode.
- Report thru step 5 while the old list has not been reached.
- Obtain next node in old list and record its predecessor node.
- If availability stack is empty then write availability stack underflow and return else copy the node andadd it to the rear of latest list.
- Set link of the last node within the new list to null and return.
If FIRST = NULL
then return (NULL)
NODENEW
AVAIL←New
LINK (AVAIL)←AVAIL
INFO (FIRST)←FIELD (NEW)
NEW←BEGIN
FIRST←SAVE
Repeat thru step 6 while (SAVE) ≠ NULL
NEW←PRED
LINK (SAVE)←SAVE
If AVAIL = NULL
then write (‘Availability stack underflow’)
Return (0)
AVAIL←else NEW
LINK (AVAIL)←AVAIL
INFO (SAVE)←FIELD (NEW)
NEW←PTR (PRED)
NULL←PTR (NEW)
Return (BEGIN)
2. Doubly linked list
1. Insertion in first
Function: DOUBINS (L, R, M, X)
NEW NODE
2. [Copy information field]
INFO (NEW) ← X
3. [Insert into an empty list]
If R = NULL
Then LPTR (NEW) ← RPTR (NULL) ← NULL
L ← R ← NEW
Return
4. [Is left most insertion?]
If M = L
Then LPTR (NEW)←NULL
RPTR (NEW) ← M
LPTR (M)← NEW
L ← NEW
Return
5. [Insert in middle]
LPTR (NEW)← LPTR (M)
RPTR (NEW) ← M
LPTR (M) ← NEW
RPTR (LPTR (NEW)) ← NEW
6. Return
2. Insertion in middle
Function: DOUBINS_ORD (L, R, M, X)
NEW NODE
2. [ Copy information field]
INFO (NEW) ← X
3. [Insert into an empty list]
If R = NULL
Then LPTR (NEW) ← RPTR (NULL) ← NULL
L ← R ← NEW
Return
4. [Does the new node precedes all other nodes in List?]
If INFO(NEW) ≤ INFO(L)
Then RPTR (NEW) ← L
LPTR(NEW)← NULL
LPTR (L) ← NEW
L ← NEW
Return
5. [Initialize temporary Pointer]
SAVE ← L
6. [Search for predecessor of latest node]
Repeat while RPTR(SAVE) ≠ NULL and INFO(NEW) ≥ INFO(RPTR(SAVE))
SAVE ← RPTR (SAVE)
7. [Set link field of latest node and its predecessor]
RPTR (NEW) ←RPTR(SAVE)
LPTR (RPTR(SAVE))←NEW
RPTR (SAVE) ← NEW
LPTR (NEW) ← SAVE
If SAVE = R
Then RPTR(SAVE)←NEW
3. Deletion in doubly link list
Function: DOUBDEL (L, R, OLD)
If R=NULL
Then write (‘UNDERFLOW’)
return
2. 2. [Delete node]
If L = R (single node in list)
Then L ← R ← NULL
else If OLD = L (left most node)
Then L ←RPTR(L)
LPTR (L) ← NULL
else if OLD = R (right most)
Then R←LPTR (R)
RPTR (R) ← NULL
else RPTR (LPTR (OLD)) ← RPTR (OLD)
LPTR (RPTR (OLD)) ←LPTR (OLD)
3. 3. [ FREE deleted node]
FREE (OLD)
3. Circular link list
1. Insertion at start
PROCEDURE: CIRCULAR_LINK_INSERT_FIRST (X, FIRST, LAST)
NEW ← NODE
2. [Initialize fields of latest node and its link to the list]
INFO (NEW) ←X
If FIRST = NULL
Then LINK (NEW) ←NEW
FIRST ← LAST ←NEW
else LINK (NEW) ← FIRST
LINK (LAST)←NEW
FIRST ←NEW
Return
2. Insertion at end
PROCEDURE: CIR_LINK_INSERT_END (X, FIRST, LAST)
NEW ←NODE
2. [Initialize fields of latest node and its link to the list]
If FIRST = NULL
Then LINK (NEW) ←NEW
FIRST ←LAST ← NEW
else LINK(NEW) ← FIRST
LINK(LAST) ← NEW
LAST ← NEW
Return
3. Insertion in between
PROCEDURE: CIR_LINK_INSERT_ORDER (X, FIRST, LAST)
NEW ← NODE
2. [Copy information content into new node
INFO (NEW) ← X
3. [Is Linked List is empty?]
If FIRST = NULL
Then LINK (NEW) ← NEW
FIRST ← LAST ← NEW
Return
4. Does new node precedes all other nodes in List?]
If INFO (NEW) ≤ INFO (FIRST)
Then LINK (NEW) ← FIRST
LINK (LAST) ← NEW
FIRST ← NEW
Return
5. [Initialize Temporary Pointer]
SAVE ← FIRST
6. [Search for Predecessor of latest node]
Repeat while SAVE ≠ LAST and INFO(NEW) ≥ INFO(LINK(SAVE))
SAVE ←LINK(SAVE)
7. [Set link field of latest node and its Predecessor]
LINK(NEW) ← LINK(SAVE)
LINK(SAVE) ← NEW
If SAVE = LAST
Then LAST ← NEW
8. [Finish]
Return
4. Deletion in circular link list
PROCEDURE: CIR_LINK_DELETE (X, FIRST, LAST)
If FIRST = NULL
Then write (‘Linked List is Empty’)
Return
2. [Initialize look for X]
SAVE ← FIRST
3. [Find X]
Repeat thru step 5 while SAVE ≠ X and SAVE ≠ LAST
4. [Update predecessor marker]
PRED ← SAVE
5. [Move to next node]
SAVE ← LINK (SAVE)
6. [End of Linked List]
If SAVE ≠ X
Then write(‘Node not found’)
return
7. [Delete X]
If X = FIRST
Then FIRST ← LINK (FIRST)
LINK (LAST) ← FIRST
else LINK (PRED) ← LINK(X)
If X = LAST
Then LAST ← PRED
8. [Free Deleted Node]
Free (X)
4. Doubly circular link list
Insertion in CDLL
1. Insertion at the top of list or in an empty list
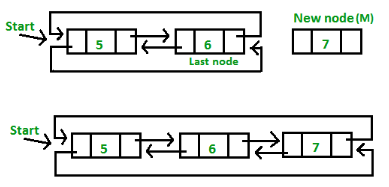
2. Insertion at the start of the list:
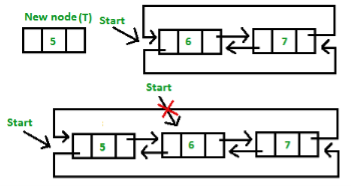
3. Insertion in between the nodes of the list: To insert a node in between the list, two data values are required one after which new node are going to be inserted and another is that the data of the new node.
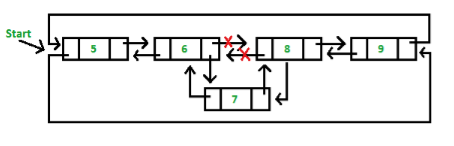
3. Deletion in CDLL
Case 1: Empty List(start = NULL)
Case 2:Initially the list contain few nodes, start points to first node of the List.
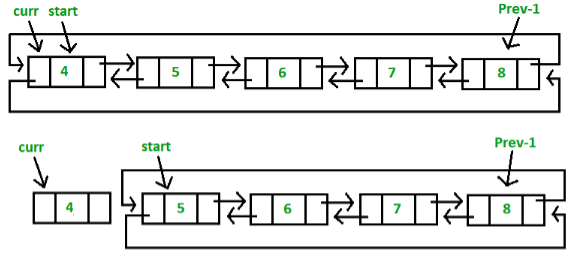
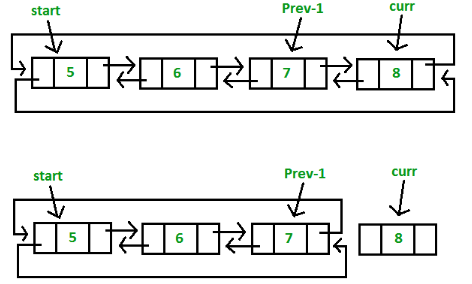
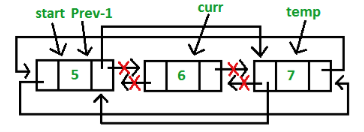
Advantages:
Disadvantages
Applications of Circular doubly linked list
Basic allocator functionality
1. malloc(n) –
2. free(p) –
To malloc a block,
When a block is freed,
node* new_node(long value, node* next)
{
node* n = (node*) malloc(sizeof(node));
n->value = value;
n->next = next;
return n;
}
A list will be identified by a node*. Hence, new_node above is also a kind of push_front, adding a new node to the beginning of a list.
Inserting a value
To insert a value, we pass a pointer to the node before the location to insert at, as well as the value to be inserted. In C, we would do
node* insert(node* p, long value)
{
node* n = new_node(value, p->next);
p->next = n;
return n;
}
Removing a node
Similarly, to remove a node, we pass a pointer to the node before it.
void remove(node* p)
{
node* n = p->next;
if(p->next)
p->next = p->next->next;
free(n);
}
Linked List as an ADT:
1. Insert
Insert ion at beginning
Insertion at end
Insertion in middle
2. Deletion
Delete from beginning
Deletion from end
Deletion from middle
3. Traverse
4. Concatenate
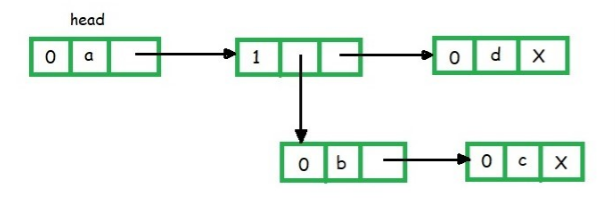
A Generalized Linked List L, is defined as a finite sequence of n>=0 elements, l1, l2, l3, l4, …,ln, such that li are either atom or the list of atoms. Thus
L = (l1, l2, l3, l4, …,ln)
where n is total number of nodes in the list.
Flag | Data | Down pointer | Next pointer |
To represent a list of items there are certain assumptions about the node structure.
Generalized linked lists are used because although the efficiency of polynomial operations using linked list is good but still, the disadvantage is that the linked list is unable to use multiple variable polynomial equation efficiently. It helps us to represent multi-variable polynomial along with the list of elements.
Typical ‘C’ structure of Generalized Linked List
typedefstruct node{
Char c; //data
int index; //flag
struct node*next,*down; //next and down pointer
} GLL;
Example of GLL {List representation}
( a, (b, c), d)
When first field is 0, it indicates that the second field is variable. If first field is 1 means the second field is a down pointer, means some list is starting.
The typical node structure will be:
Flag | Var | Exp | Next pointer |
Example:
9x5 + 7xy4 + 10xz
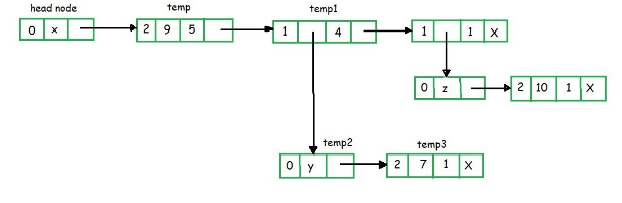
In the above example the top node is of variable x. The temp node shows the primary field as 2 means coefficient and exponent are present.

Since temp node is attached to go node and head node has variable x, temp node having coefficient = 9 and exponent = 5. The above two nodes are often read as 9x5.
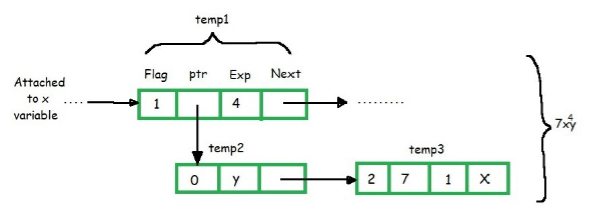
Similarly, within the above figure, the node temp1 are often read as x4.
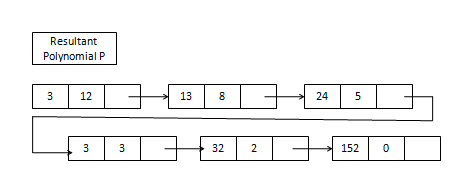
A linked list that's wont to store Polynomial seems like –
For all power, we'll check for the coefficients of the exponents that have an equivalent value of exponents and add them.
Input - Polynomial P1 and P2 represented as a linked list.
Polynomial
P1= 13x8 +7x5 + 32x2 +54
P2=3x12 +17x5 + 3x3 +98
Algorithm
Resultant polynomial
P =3x12 +13x8 +24x5 +3x3 +32x2 +152
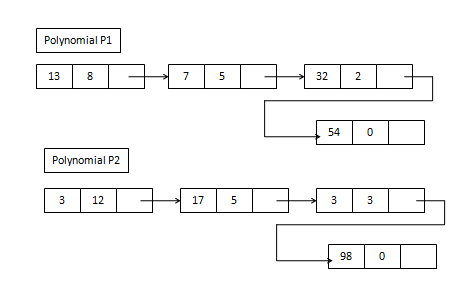
Resultant polynomial after adding 2 polynomials p1 and p2