5.1 Basic concept | unit 5 stack

FDS

Unit 5

Stack

5.1 Basic concept

Stack

A stack could also be a container of objects that are inserted and removed according to the last-in first-out (LIFO) principle.

Within the pushdown stacks only two operations are allowed: push the item into the stack, and pop the item out of the stack.

A stack could also be a limited access arrangement - elements are often added and away from the stack only at the very best.

Push adds an item to the very best of the stack, pop removes the item from the very best. A helpful analogy is to think about a stack of books; you'll remove only the very best book, also you'll add a replacement book on the very best.

A stack may be a recursive arrangement. Here may be a structural definition of a Stack: a stack is either empty or it consists of a top and thus the remainder which can be a stack;

A stack could also be a linear arrangement during which all the insertion and deletion of data otherwise you'll say its values are done at one end only, rather than within the middle. Stacks are often implemented by using arrays of type linear.

The stack is usually utilized in converting and evaluating expressions in Polish notations, i.e.:

Infix
Prefix
Postfix

Applications of stacks

The only application of a stack is to reverse a word. You push a given word to stack - letter by letter - then pop letters from the stack.

Another application is an "undo" mechanism in text editors; this operation is accomplished by keeping all text changes during a stack.

Backtracking. This is often a process once you bought to access the foremost recent data element during a series of elements. Consider a labyrinth or maze - how do i find how from an entrance to an exit?

Once you reach a dead end, you want to backtrack. But backtrack to where? To the previous choice point. Therefore, at each choice point you store on a stack all alternatives. Then backtracking simply means popping a next choice from the stack.

Language processing:

Space for parameters and native variables is made internally employing a stack.

Compiler's syntax check for matching braces is implemented by using stack.

support for recursion

5.2 Stack as Abstract Data Type

Stack as abstract data types

In Stack ADT Implementation rather than data being stored in each node, the pointer to data is stored.

The program allocates memory for the info and the address is passed to the stack ADT.

The head node and therefore the data nodes are encapsulated within the ADT. The calling function will only watch for the pointer to the stack.

The stack head structure also contains a pointer to the top and count of the number of entries currently in the stack.

A Stack contains elements of an equivalent type arranged in sequential order. All operations happen at one end that's top of the stack and the following operations are often performed:

Operations on stacks

Stack() creates a replacement stack that's empty. It doesn't require any parameters and returns an empty stack.

push(item) adds a replacement item to the highest of the stack. It needs the item and returns nothing.

pop() removes the highest item from the stack. It doesn't require any parameters and returns the item. The stack is modified.

peek() returns the highest item from the stack but doesn't remove it. It doesn't require parameters. The stack isn't modified.

isEmpty() tests to ascertain whether the stack is empty. It doesn't require any parameters and returns a boolean value.

size() returns the number of things on the stack. It needs no parameters and returns an integer.

The stacks of elements of any particular type may be a finite sequence of elements of that type alongside the subsequent operations:

initialize the stack to be empty

Determine whether the stack is empty or not

Check whether the stack is full or not

If the stack isn't full, add or insert a replacement node at the highest of the stack. This operation is termed as Push Operation

If the stack isn't empty, then retrieve the node at its top

If the stack isn't empty, the delete the node at its top.

This operation is named as push, pop peek

5.3 Representation of Stacks Using Sequential Organization

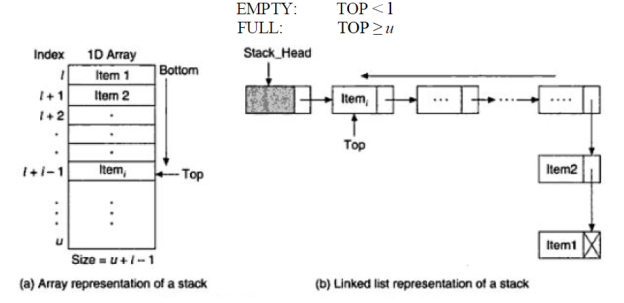
REPRESENTATION OF A STACK

A stack could also be represented within the memory in various ways. There are two main ways:

using a one-dimensional array
one linked list.

Array Representation of Stacks

First we've to allocate a memory block of sufficient size toaccommodate the complete capacity of the stack. Then, ranging from the primary location of the memory block, the items of the stack are often stored during a sequential fashion.

In Figure, Item i denotes the ith item within the stack;

l and u denote the index range of the array in use; usuallythe values of those indices are 1 and SIZE respectively.

TOP may be a pointer to point the position of the array upto which it's crammed with the things of the stack.

With this representation, the subsequent two ways are often stated

Linked List Representation of Stacks

Although array representation of stacks is extremely easy and convenientbut it allows the representation of only fixed sized stacks.

In several applications, the dimensions of the stack may vary during program execution.

A clear solution to the present problem is to represent a stack employing a linkedlist.

One linked list structure is sufficient to represent any stack. Here, the info field is for the ITEM,and the LINK field is, as usual, to point to the next' item. Above Figure b depicts such a stack employing a single linked list.

In the linked list representation, the primary node on the list is that the current item that's the item at the highest of thestack and therefore the last node is that the node containing the bottom-most item. Thus, a PUSH operation will add a replacement node within the front and a POP operation will remove a node from the front of the list.

$C:\Users\Kilua Zoldyck\Pictures\llkm.png$

5.4 Stack operations

Algorithms for Stack Operations – PUSH, POP, PEEP

A linear list which allows insertion and deletion of a component at one end only is named stack.

The insertion operation is named as PUSH and deletion operation as POP.

The most and least accessible elements in stack are referred to as top and bottom of the stack respectively.

Since insertion and deletion operations are performed at one end of a stack, the weather can only beremoved within the opposite orders from that during which they were added to the stack; such a linear list is mentioned as a LIFO (last in first out) list.

$C:\Users\Kilua Zoldyck\Pictures\1.png$

A pointer TOP keeps track of the highest element within the stack. Initially, when the stack is empty, TOP features a value of “one” then on.

Each time a replacement element is inserted within the stack, the pointer is incremented by “one” before, the element is placed on the stack. The pointer is decremented by “one” whenever a deletion is formed from the stack.

Procedure: PUSH (S, TOP, X)

This procedure inserts a component x to the highest of a stack which is represented by a vector S containing Nelements with a pointer TOP denoting the highest element within the stack.

1. [Check for stack overflow]

If TOP ≥ N

Then write (‘STACK OVERFLOW’)

Return

2. [Increment TOP]

TOP ←TOP + 1

3. [Insert Element]

[STOP] ←X

4. [Finished]

Return

Function: POP (S, TOP)

This function removes the highest element from a stack which is represented by a vector S and returns thiselement. TOP may be a pointer to the highest element of the stack.

1. [Check for underflow of stack]

If TOP = 0

Then Write (‘STACK UNDERFLOW ON POP’)

Take action in response to underflow

Return

2. [Decrement Pointer]

TOP ← TOP – 1

3. [Return former top element of stack]

Return (S[TOP + 1])

Function: PEEP (S, TOP, I)

This function returns the worth of the ith element from the highest of the stack which is represented by a vectorS containing N elements. The element isn't deleted by this function.

1. [Check for stack Underflow]

If TOP - I +1 ≤ 0

Then Write (‘STACK UNDERFLOW ON PEEP’)

Take action in response to Underflow

Exit

2. [Return Ith element from top of the stack

Return (S[TOP – I + 1])

Write an algorithm to vary the ith value of stack to value X

PROCEDURE: CHANGE (S, TOP, X, I)

This procedure changes the worth of the Ith element from the highest of the stack to the worth containing in X.

Stack is represented by a vector S containing N elements.

1. [Check for stack Underflow]

If TOP – I + 1 ≤ 0

Then Write (‘STACK UNDERFLOW ON CHANGE’)

Return

2. [Change Ith element from top of the stack]

S[TOP – I + 1] ← X

3. [Finished]

Return

Algorithm for push, pop and empty operations on stack.

Algorithm RECOGNIZE

Given an input string named STRING on alphabet ‘a’ and ‘b’ which contain blank (‘ ‘) on right most character

Function NEXTCHAR which returns subsequent symbol from STRING. This algorithm determines if an input string is of form ai bi where i>1 i.e. no of ‘a’ should be adequate to no of ‘b’. The vector S represent the stack and TOP isthe pointer to the highest element of stack. Counter may be a counter B for ‘b’ occurrence.

1. [Initialize stack and counter]

TOP←0

COUNTER_B ←0

2. [Get and stack character ‘a’ from whole string and count the occurrence of ‘b’ ]

NEXT ←NEXTCHAR(STRING)

Repeat while NEXT != ‘ ‘

IF NEXT = ‘a’

Then PUSH (S, TOP, NEXT)

Else COUNTER_B ←COUNTER_B+1

NEXT ←NEXTCHAR(STRING)

3. [Pop the stack until empty and decrement the COUNTER_B]

Repeat while TOP != 0

POP (S,TOP)

COUNTER_B←COUNTER_B-1

4. [Check for grammar]

If COUNTER_B != 0

Then write (‘INVALID STRING’)

Else write (‘VALID STRING’)

What is recursion? Write a C program for GCD using recursion.

Recursion

A procedure that contains a procedure call to itself or a procedure call to second procedure whicheventually causes the primary procedure to be called is understood as recursive procedure.

There are two important conditions that has got to be satisfied by any recursive procedure

whenever a procedure calls itself it must be nearer in some sense to an answer

There must be a choice criterion for stopping the method or computation

There are two sorts of recursion

Primitive Recursion: this is often recursive defined function. E.g. Factorial function

Non-Primitive Recursion: this is often recursive use of procedure. E.g. Find GCD of given two numbers

C program for GCD using recursion

#include

intFind_GCD(int, int);

void main()

{

int n1, n2, gcd;

scanf(“%d %d”,&n1, &n2);

gcd = Find_GCD(n1, &n2);

printf(“GCD of a kid and a light is %d”, n1, n2, gcd);

}

intFind_GCD(int m, int n)

{

intgcdVal;

if(n>m)

{

gcdVal = Find_GCD(n,m);

}

else if(n==0)

{

gcdVal = m;

}

else

{

gcdVal = Find_GCD(n, m%n);

}

return(gcdVal);

}

Algorithm for factorial

Algorithm: FACTORIAL

Given integer N, this algorithm computes factorial of N. Stack A is employed to store an activation record associatedwith each recursive call. Each activation record contains the present value of N and therefore the current addressRET_ADDE.TEMP_REC is additionally a record which contains two variables PARAM & ADDRESS.TOP may be a pointer to thetop element of stack A. Initially address is about to the most calling address. PARAM is about to initial value N.

1. [Save N and return Address]

CALL PUSH (A, TOP, TEMP_REC)

2. [Is the bottom criterion found?]

If N=0

Then FACTORIAL1

GO TO Step 4

Else PARAM←N-1

ADDRESS←Step 3

GO TO Step 1

3. [Calculate N!]

FACTORIAL←N * FACTORIAL

4. [Restore previous N and return address]

TEMP_REC←POP(A,TOP)

(i.e., PARAM←N, ADDRESSRET_ADDR)

GO TO ADDRESS

5.5 Multiple Stacks

Multiple stacks

When a stack is made using a single array, we will unable to store a great deal of knowledge, thus this problem is rectified using quite one stack within the same array of sufficient array. This system is named as Multiple Stack.

When an array of STACK[n] is employed to represent two stacks, say Stack A and Stack B. Then the worth of n is such the combined size of both the Stack[A] and Stack[B] will never exceed n. Stack[A] will grow from left to right, whereas Stack[B] will grow in another way i.e.) right to left.

Create a structure k Stacks that represents k stacks. Implementation of k Stacks should use just one array, i.e., k stacks should use an equivalent array for storing elements. The following functions must be supported by k stacks.

push(int x, intsn) –> pushes x to stack number ‘sn’ where sn is from 0 to k-1

pop(intsn) –> pops a component from stack number ‘sn’ where sn is from 0 to k-1

Method 1 (Divide the array in slots of size n/k)

A simple thanks to implementing k stacks is to divide the array in k slots of size n/k each, and fix the slots for various stacks, i.e., use arr[0] to arr[n/k-1] for the first stack, and arr[n/k] to arr[2n/k-1] for stack2 where arr[] is that the array to be wont to implement two stacks and size of the array be n.

The problem with this method is the inefficient use of array space. A stack push operation may end in stack overflow albeit there's space available in arr[]. for instance, say the k is 2 and array size (n) is 6 and that we push 3 elements to first and don't push anything to the second stack. once we push 4th element to first, there'll be overflow albeit we've space for 3 more elements in the array

Method 2 (A space-efficient implementation)

The idea is to use two extra arrays for the efficient implementation of k stacks in an array. This might not make much sense for integer stacks, but stack items are often large for instance stacks of employees, students, etc where every item is of many bytes. For such large stacks, the additional space used is relatively very less as we use two integer arrays as extra space.

The following are the 2 extra arrays are used:

top[]: this is often of size k and stores indexes of top elements altogether stacks.

next[]: this is often of size n and stores indexes of next item for the things in array arr[]. Here arr[] is an actual array that stores k stacks.

Together with k stacks, a stack of free slots in arr[] is additionally maintained. the highest of this stack is stored during a variable ‘free’.

All entries in top[] are initialized as -1 to point that each one stack are empty. All entries next[i] are initialized as i+1 because all slots are free initially and pointing to the next slot. Top of the free stack, ‘free’ is initialized as 0.

Time complexities of operations push() and pop() is O(1).

The best a part of implementing multiple stacks is, if there's a slot available in stack, then an item are often pushed in any of the stacks, i.e., no wastage of space.

5.6 Applications of Stack- Expression Evaluation and Conversion

Applications of stack

Recursion

Tail recursion
Non tail recursion
Indirect recursion
Nested recursion

Keeping track of function calls

Evaluation of expressions

Infix to postfix
Prefix to postfix
Postfix evaluations

Reversing characters

Servicing hardware interrupts

Tower of Hanoi

Fibonacci series

Solving combinatorial problems using backtracking.

5.7 Polish notation and expression conversion

Infix: The notation commonly utilized in mathematical formulae

Operand: the worth on which an operator is performed

Operator: a logo like minus that shows an operation

Postfix: A notation during which operators follow operands

Prefix: A notation during which operands follow operators

Reverse prefix notation (RPN): A notation during which operators follow operands

Infix-

Infix notation is seen a the “normal” thanks to creating mathematical formulae. we will take an easy addition sum

A+B

Prefix

Prefixnotation puts the operator before all of the operands. this suggests that the precedence is usually clear

+AB

Postfix

Postfix OR Reverse prefix notation in Postfix notation puts the operator before all of the operands.

This is a bit like the Lukasiewicz notation, but the operand comes at the top of the expression and similarly removes the necessity for brackets within any expressions.

It is called Polish thanks to the nationality of Jan Łukasiewicz who invented the notation.

AB+

5.8 Need for prefix and postfix expressions

Infix isn't the sole possible thanks to develop expressions, although it's quite easy for people to know. Computers are likely to use a stack to guage expressions — and thus Reverse prefix notation is usually used because it may be a good way to easily evaluate an expression employing a stack.

Algorithm for Prefix to Postfix:

Read the Prefix expression in reverse order (from right to left)

If the symbol is an operand, then push it onto the Stack

If the symbol is an operator, then pop two operands from the Stack

Create a string by concatenating the two operands and the operator after them.

string = operand1 + operand2 + operator

And push the resultant string back to Stack

Repeat the above steps until end of Prefix expression.

Postfix notation

Notation is defined as a way of writing arithmetic operations

Notation can be write as 3 ways

Prefix notation- operator are infixed to operands e.g.- +ab
Infix notation - simplest way of writing e.g.-a+b
postfix operators is prefixed to operands e.g.- ab+

Sr.No.	Infix Notation	Prefix Notation	Postfix Notation
1	a + b	+ a b	ab+
2	(a + b) ∗ c	*+abc	a b + c ∗
3	a ∗ (b + c)	∗ a + b c	a b c + ∗
4	a / b + c / d	+ / a b / c d	a b / c d / +
5	(a + b) ∗ (c + d)	∗ + a b + c d	a b + c d + ∗
6	((a + b) ∗ c) - d	- ∗ + a b c d	a b + c ∗ d -

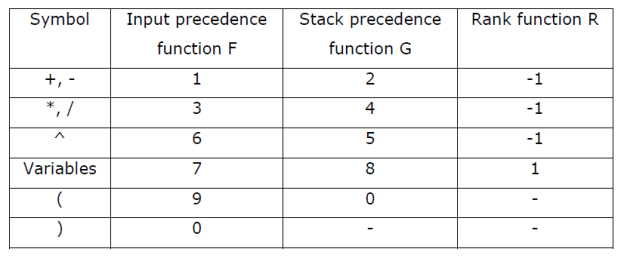
Precedence

When an operator is between two operands precedence decides which operator will be first evaluated

a+b*c a+(b*c)

Associativity

Associativity is the rule where operators with the same precedence appear in an expression

S no	Operator	Operator	Precedence	Associativity
1	Exponentiation	^	Highest	Right associative
2	Multiplication and division	‘*’ and ‘/’	Second highest	Left associative
3	Addition and subtraction	+ and -	Lowest	Left associative

5.9 Postfix expression evaluation

Step 1 − scan the expression from left to right

Step 2 − if it is an operand push it to stack

Step 3 − if it is an operator pull operand from stack and perform operation

Step 4 − store the output of step 3, back to stack

Step 5 − scan the expression until all operands are consumed

Step 6 − pop the stack and perform operation

Algorithm to convert infix to postfix

$C:\Users\Kilua Zoldyck\Pictures\2.png$

Algorithm: REVPOL

Given an input string INFIX containing an infix expression which has been padded on the proper with ‘)’ andwhose symbol have precedence value given by above table, a vector S used as a stack and a NEXTCHARwhich when invoked returns subsequent character of its argument. This algorithm converts INFIX into reversepolish and places the end in the string POLISH. The integer variable TOP denotes the highest of the stack.

Algorithm PUSH and POP are used for stack manipulation. The integer variable RANK accumulates the rankof expression. Finally the string variable TEMP is employed for temporary storage purpose.

1. [Initialize stack]

TOP ←1

S[TOP] ←‘(‘

2. [Initialize output string and rank count]

POLISH ←‘ ‘

RANK ←0

3. [Get first input symbol]

NEXT←NEXTCHAR (INFIX)

4. [Translate the infix expression]

Repeat thru step 7 while NEXT != ‘ ‘

5. [Remove symbols with greater precedence from stack]

IF TOP < 1

Then write (‘INVALID’)

EXIT

Repeat while G (S[TOP]) > F(NEXT)

TEMP ←POP (S, TOP)

POLISH ←POLISH O TEMP

RANK ←RANK + R(TEMP)

IF RANK <1

Then write ‘INVALID’)

EXIT

6. [Are there matching parentheses]

IF G(S[TOP]) != F(NEXT)

Then call PUSH (S,TOP, NEXT)

Else POP (S,TOP)

7. [Get next symbol]

NEXT ←NEXTCHAR(INFIX)

8. [Is the expression valid]

IF TOP != 0 OR RANK != 1

Then write (‘INVALID ‘)

Else write (‘VALID ’)

Trace the conversion of infix to postfix form in tabular form.

(i) (A + B * C / D - E + F / G / ( H + I ) )

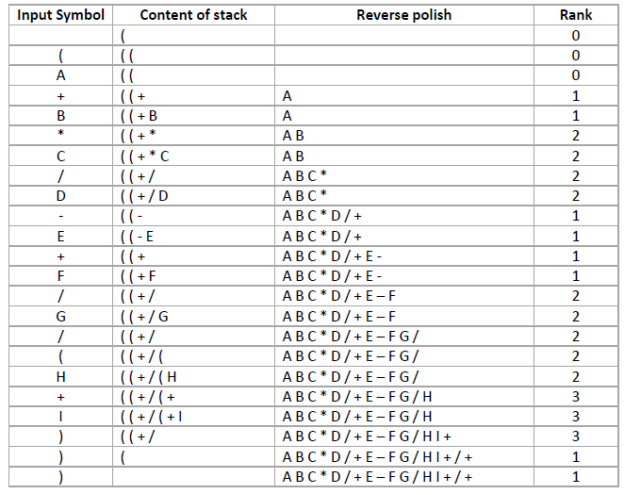
$C:\Users\Kilua Zoldyck\Pictures\23.png$

Postfix expression is: A B C * D / + E – F G / H I + / +

5.10 Linked Stack and Operations

Implement a stack using single linked list concept.

All the only linked list operations perform supported Stack operations LIFO(last in first out) and with the assistance of that knowledge we are getting to implement a stack using single linked list.

Using single linked lists so the way to implement here it's linked list means what we are storing the knowledge within the sort of nodes and that we got to follow the stack rules and that we got to implement using single linked list nodes

Implementation

A stack are often easily implemented through the linked list.

In stack Implementation, a stack contains a top pointer. which is “head” of the stack where pushing and popping items happens at the top of the list.

first node have null in link field and second node link have first node address in link field then on and last node address in “top” pointer.

The main advantage of using linked list over an arrays is that it's possible to implements a stack which will shrink or grow the maximum amount as required .

In using array will put a restriction to the utmost capacity of the array which may cause stack overflow. Here each new node are going to be dynamically allocate.

so overflow isn't possible.

Linked list implementation of stack

Instead of using array, we will also use linked list to implement stack. Linked list allocates the memory dynamically. However, time complexity in both the scenario is same for all the operations i.e. push, pop and peek.

Adding a node to the stack (Push operation)

Adding a node to the stack is mentioned as push operation.

Pushing a component to a stack in linked list implementation is different from that of an array implementation.

so as to push a component onto the stack, the subsequent steps are involved.

Create a node first and allocate memory thereto.

If the list is empty then the item is to be pushed because the start node of the list. This includes assigning value to the info a part of "> a part of the node and assign null to the address part of the node.

If there are some nodes within the list already, then we've to feature the new element within the beginning of the list (to not violate the property of the stack). For this purpose, assign the address of the starting element to the address field of the new node and make the new node, the starting node of the list.

Time Complexity : o(1)

Deleting a node from the stack (POP operation)

Deleting a node from the highest of stack is mentioned as pop operation. Deleting a node from the linked list implementation of stack is different from that within the array implementation. so as to pop a component from the stack, we'd like to follow the subsequent steps :

Check for the underflow condition: The underflow condition occurs once we attempt to pop from an already empty stack. The stack are going to be empty if the top pointer of the list points to null.

Adjust the top pointer accordingly: In stack, the weather are popped only from one end, therefore, the worth stored within the head pointer must be deleted and therefore the node must be freed. subsequent node of the top node now becomes the top node.

Time Complexity : o(n)

Display the nodes (Traversing)

Displaying all the nodes of a stack needs traversing all the nodes of the linked list organized within the sort of stack. For this purpose, we'd like to follow the subsequent steps.

Copy the top pointer into a short lived pointer.

Move the temporary pointer through all the nodes of the list and print the worth field attached to each node.

Time Complexity : o(n)

5.11 Recursion- concept, variants of recursion- direct, indirect, tail and tree

Recursion

The process during which a function calls itself directly or indirectly is named as recursion

The corresponding function is named as recursive function. Using recursive algorithm, certain problems are often solved quite easily. Examples of such problems are Towers of Hanoi (TOH), Inorder/Preorder/Postorder Tree Traversals, DFS of Graph, etc.

Base condition for recursion

In the recursive program, the answer to the bottom case is provided and therefore the solution of the larger problem is expressed in terms of smaller problems.

Sub-problems are easier to solve than the original problem

Solutions to sub-problems are combined to solve the original problem

Recursion function for factorial

int fact(int n)

{

if (n < = 1) // base case

return 1;

else

return n*fact(n-1);

}

In the above example, base case for n < = 1 is defined and bigger value of number are often solved by converting to smaller one till base case is reached.

Recursion process

The idea is to represent a drag in terms of 1 or more smaller problems, and add one or more base conditions that stop the recursion.

For example, we compute factorial n if we all know factorial of (n-1). The base case for factorial would be n = 0. We return 1 when n = 0.

Divide-and-conquer” is most often used to traverse or search data structures such as binary search trees, graphs, and heaps. It also works for many sorting algorithms, like quicksort and heapsort.

Recursion causes stack overflow

If the bottom case isn't reached or not defined, then the stack overflow problem may arise. Let us take an example to understand this.

Factorial using recursion

int fact(int n)

{

// wrong base case (it may cause // stack overflow).

if (n == 100)

return 1;

else

return n*fact(n-1);

}

If fact(10) is named , it'll call fact(9), fact(8), fact(7) then on but the amount will never reach 100. So, the bottom case isn't reached. If the memory is exhausted by these functions on the stack, it'll cause a stack overflow error.

Direct and indirect recursion

A function fun is named direct recursive if it calls an equivalent function fun.

A function fun is named indirect recursive if it calls another function say fun_new and fun_new calls fun directly or indirectly.

// An example of direct recursion

voiddirectRecFun()

{

// Some code....

directRecFun();

// Some code...

}

// An example of indirect recursion

void indirectRecFun1()

{

// Some code...

indirectRecFun2();

// Some code...

}

void indirectRecFun2()

{

// Some code...

indirectRecFun1();

// Some code...

}

Tail and non tail recursion

A recursive function is tail recursive when recursive call is that the last item executed by the function. Please refer tail recursion article for details.

Allocation of memory to different function calls in recursion

When any function is named from main(), the memory is allocated thereto on the stack.

A recursive function calls itself, the memory for a called function is allocated on top of memory allocated to calling function and different copy of local variables is made for every call.

When the bottom case is reached, the function returns its value to the function by whom it's called and memory is de-allocated and therefore the process continues.

5.12 Backtracking algorithmic strategy

Backtracking is an algorithmic-technique for solving problems recursively by trying to create an answer incrementally, one piece at a time, removing those solutions that fail to satisfy the constraints of the matter at any point of your time (by time, here, is mentioned the time elapsed till reaching any level of the search tree).

Backtracking are often defined as a general algorithmic technique that considers searching every possible combination so as to unravel a computational problem.

Problems in backtracking

Decision Problem – during this, we look for a feasible solution.

Optimization Problem – during this, we look for the simplest solution.

Enumeration Problem – during this, we discover all feasible solutions.

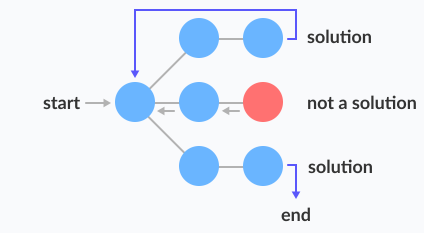
$C:\Users\Kilua Zoldyck\Pictures\bt.png$

Backtrack algorithm

Backtrack(x)

if x is not a solution

return false

if x is a new solution

add to list of solutions

backtrack(expand x)

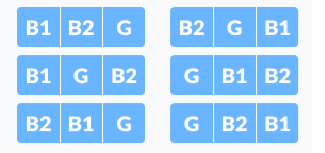
Example- Find all the possible ways of arranging 2 boys and 1 girl on 3 benches. Constraint: Girl should not be on the middle bench.

Solution There are a total of 3! = 6 possibilities. We will try all the possibilities and get the possible solutions. We recursively try all the possibilities.

Possible condition

$C:\Users\Kilua Zoldyck\Pictures\bt2.png$

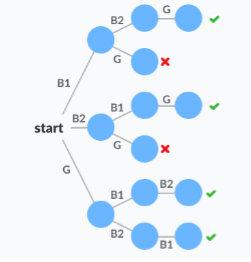
$C:\Users\Kilua Zoldyck\Pictures\bt5.png$

5.13 Use of stack in backtracking.

Backtracking

Backtracking is one among the algorithm designing technique.

For that purpose, we dive into how, if that way isn't efficient, we come to the previous state and enter another paths.

To urge back from current state, we'd like to store the previous state. For that purpose, we'd like stack.

Some samples of backtracking is finding the answer for Knight Tour problem or N-Queen Problem etc.

Backtracking using stack rat maze problem

A Maze is given as N*M binary matrix of blocks and there's a rat initially at (0, 0) i.e. maze[0][0] and therefore the rat wants to eat food which is present at some given block within the maze (fx, fy).

During a maze matrix, 0 means the block may be a dead end and 1 means the block are often utilized in the trail from source to destination. The rat can move in any direction (not diagonally) to any block provided the block isn't a dead end.

The task is to see if there exists any path in order that the rat can reach the food or not. It’s not needed to print the trail.

Recursion uses a call stack to stay the shop each recursive call then pop because the function ends. We’ll eliminate recursion by using our own stack to try to to an equivalent thing.

A node structure is employed to store the (i, j) coordinates and directions explored from this node and which direction to undertake out next.

Structure Used:

X : x coordinate of the node

Y : y coordinate of the node

dir: This variable are going to be wont to tell which all directions we've tried and which to settle on next. We’ll try all the directions in anti-clockwise manner ranging from Up. Initially it'll be assigned 0.

If dir=0 try Up direction.

If dir=1 try left direction.

If dir=2 try down direction.

If dir=3 try right direction.

Else retract back to the previous block of the maze.

Procedure

Initially, we'll push a node with indexes i=0, j=0 and dir=0 into the stack.

We’ll move to all or any the direction of the topmost node one by one in an anti-clockwise manner and every time as we try a replacement path we'll push that node (block of the maze) within the stack.

We’ll increase dir variable of the topmost node whenever in order that we will try a replacement direction whenever unless all the directions are explored i.e.dir=4.

If dir equals to 4 we'll pop that node from the stack meaning we are retracting one step back to the trail where we came from.

We will also maintain a visited matrix which can maintain which blocks of the maze are already utilized in the trail or in other words present within the stack. While trying out any direction we'll also check if the block of the maze isn't a dead end and isn't out of the maze too.

We will do that while either the topmost node coordinates become adequate to the food’s coordinates meaning we've reached the food or the stack becomes empty which suggests that there's no possible path to succeed in the food.

Maze[4][5] = {

{1, 0, 1, 1, 0},

{1, 1, 1, 0, 1},

{0, 1, 0, 1, 1},

{1, 1, 1, 1, 1}

}

fx = 2, fy=3

Path Found!

The path can be: (0, 0) -> (1, 0) -> (1, 1) -> (2, 1) -> (3, 1) -> (3, 2) -> (3, 3) -> (2, 3)