6.1 Basic concept | unit 6 queue

FDS

Unit 6

Queue

6.1 Basic concept

Queue

Queue is additionally an abstract data type or a linear arrangement , a bit like stack arrangement , during which the primary element is inserted from one end called the REAR(also called tail), and therefore the removal of existing element takes place from the opposite end called as FRONT(also called head).

This makes queue as FIFO(First in First Out) arrangement, which suggests that element inserted first are going to be removed first.

For e.g. If you attend a ticket counter to shop for movie tickets, and are first within the queue, then you'll be the primary one to urge the tickets. Right? Same is that the case with Queue arrangement.

Data inserted first, will leave the queue first.

The process to feature a component into queue is named Enqueue.

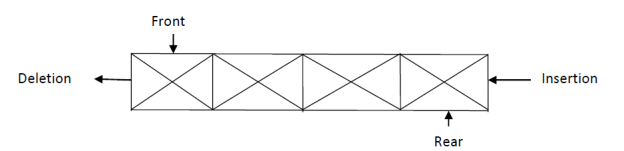
The process of removal of a component from queue is named Dequeue.

Basic features of Queue

Queue is an ordered list of elements of comparable data types.

Queue may be a FIFO (First in First Out) structure.

Once a replacement element is inserted into the Queue, all the weather inserted before the new element within the queue must be removed, to get rid of the new element.

peek ( ) function is often want to return the worth of first element without dequeuing it.

Applications of Queue

Queue is used to manage any group of objects in an order during which the primary one coming in, also gets out first while the others await their turn, like within the following scenarios:

Serving requests on one shared resource, sort of a printer, CPU task scheduling etc.

In real world scenario, call centre phone systems uses Queues to carry people calling them in an order, until a service representative is free.

Handling of interrupts in real-time systems. The interrupts are handled within the same order as they arrive i.e. First come first served.

Implementation of Queue arrangement

Queues are often implemented using an Array, Stack or Linked List. the simplest way of implementing a queue is by using an Array.

Initially the head (FRONT) and therefore the tail (REAR) of the queue points at the primary index of the array (starting the index of array from 0). As we add elements to the queue, the tail keeps on moving ahead, always pointing to the position where subsequent element are going to be inserted, while the top remains at the primary index.

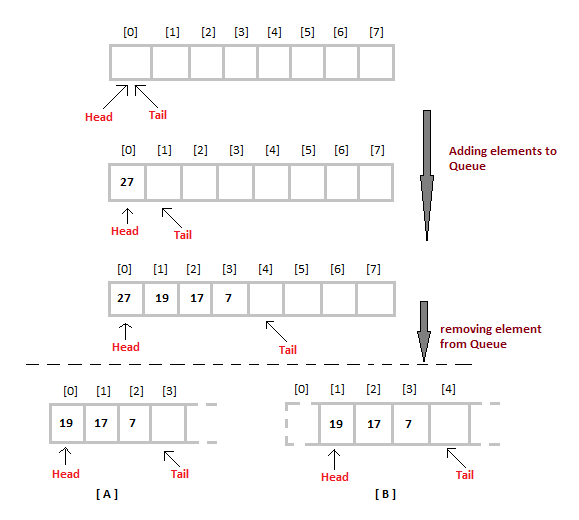
$C:\Users\Kilua Zoldyck\Pictures\s.png$

When we remove a component from Queue, we will follow two possible approaches (mentioned [A] and [B] in above diagram). In [A] approach, we remove the element at head position, then one by one shift all the opposite elements in forward position.

In approach [B] we remove the element from head position then move head to subsequent position.

In approach [A] there's an overhead of shifting the weather one position forward whenever we remove the primary element.

In approach [B] there's no such overhead, but whenever we move head one position ahead, after removal of first element, the dimensions on Queue is reduced by one space whenever

1. Queue

A linear list which allows deletion to be performed at one end of the list and insertion at the opposite end is named queue.

The information in such an inventory is processed FIFO (first in first out) of FCFS (first come first served) pattern.

Front is that the end of queue from that deletion is to be performed

Rear is that the end of queue at which new element is to be inserted.

The process to feature a component into queue is named Enqueu.

The process of removal of a component from queue is named Dequeue.

The familiar and traditional example of a queue is queue at Supermarket register where the primary person in line is typically the primary to be verified.

$C:\Users\Kilua Zoldyck\Pictures\1.png$

6.2 Queue as Abstract Data Type

A queue is an object or more specifically as abstract data structure that permits the subsequent operations

Enqueue: Add a component to the top of the queue

Dequeue: Remove a component from the front of the queue

IsEmpty: Check if the queue is empty.

IsFull: Check if the queue is full.

Peek: Get the worth of the front of the queue without removing it

Working of Queue

Queue operations work as follows:

two pointers FRONT and REAR

FRONT track the primary element of the queue

REAR track the last elements of the queue

initially, set value of FRONT and REAR to -1

Enqueue Operation

check if the queue is full

for the primary element, set value of FRONT to 0

increase the REAR index by 1

add the new element within the position pointed to by REAR

Dequeue Operation

check if the queue is empty

return the worth pointed by FRONT

increase the FRONT index by 1

for the last element, reset the values of FRONT and REAR to -1

Complexity Analysis of Queue Operations

Just like Stack, in case of a Queue too, we know exactly, on which position new element will be added and from where an element will be removed, hence both these operations requires a single step.

Enqueue: O(1)

Dequeue: O(1)

Size: O(1)

6.3 Representation of Queue using Sequential organization

Representation of queue using arrays

H	E	L	L	O

0 1 2 3 4 5 6

Front=0 rear=4

Algorithm to insert any element in a queue

Step 1: IF REAR = MAX - 1

Write OVERFLOW

Go to step

[END OF IF]

Step 2: IF FRONT = -1 and REAR = -1

SET FRONT = REAR = 0

ELSE

SET REAR = REAR + 1

[END OF IF]

Step 3: Set QUEUE[REAR] = NUM

Step 4: EXIT

0 1 2 3 4 5 6

Front=0 rear=5

Algorithm to delete an element from the queue

If, the value of front is -1 or value of front is greater than rear , write an underflow message and exit.

Otherwise, keep increasing the value of front and return the item stored at the front end of the queue at each time.

Algorithm

Step 1: IF FRONT = -1 or FRONT > REAR

Write UNDERFLOW

ELSE

SET VAL = QUEUE[FRONT]

SET FRONT = FRONT + 1

[END OF IF]

Step 2: EXIT

0 1 2 3 4 5 6

Front=1 rear=5

Queue using link list

To implement queue using linked list,

Step 1 - Include all the header files which are used in the program. And declare all the user defined functions.

Step 2 - Define a 'Node' structure with two members data and next.

Step 3 - Define two Node pointers 'front' and 'rear' and set both to NULL.

Step 4 - Implement the main method by displaying Menu of list of operations and make suitable function calls in the main method to perform user selected operation.

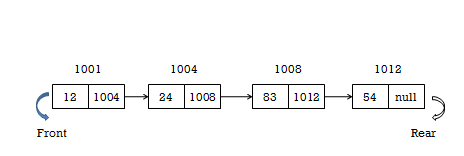
$C:\Users\Kilua Zoldyck\Pictures\asa.png$

1. To insert a new node into the queue...

enQueue(value) - Inserting an element into the Queue

Step 1 - Create a newNode with given value and set 'newNode → next' to NULL.

Step 2 - Check whether queue is Empty (rear == NULL)

Step 3 - If it is Empty then, set front = newNode and rear = newNode.

Step 4 - If it is Not Empty then, set rear → next = newNode and rear = newNode.

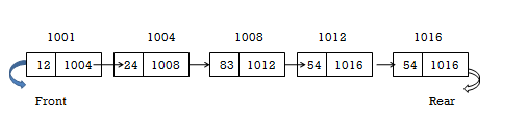
$C:\Users\Kilua Zoldyck\Pictures\swq.png$

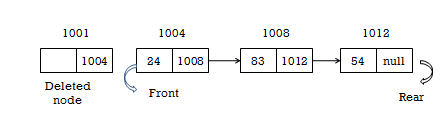
2. To delete a node from the queue

deQueue() - Deleting an Element from Queue

Step 1 - Check whether queue is Empty (front == NULL).

Step 2 - If it is Empty, then display "Queue is Empty!!! Deletion is not possible!!!" and terminate from the function

Step 3 - If it is Not Empty then, define a Node pointer 'temp' and set it to 'front'.

Step 4 - Then set 'front = front → next' and delete 'temp' (free(temp)).

$C:\Users\Kilua Zoldyck\Pictures\aqawq.png$

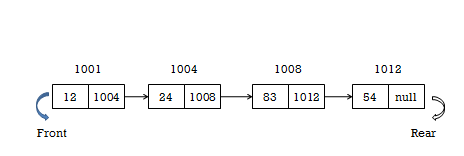
3. To display the elements (nodes) of a queue...

display() - Displaying the elements of Queue

Step 1 - Check whether queue is Empty (front == NULL).

Step 2 - If it is Empty then, display 'Queue is Empty!!!' and terminate the function.

Step 3 - If it is Not Empty then, define a Node pointer 'temp' and initialize with front.

Step 4 - Display 'temp → data --->' and move it to the next node. Repeat the same until 'temp' reaches to 'rear' (temp → next != NULL).

Step 5 - Finally! Display 'temp → data ---> ‘NULL’

$C:\Users\Kilua Zoldyck\Pictures\asa.png$

6.4 Queue Operations

1. Enqueue

Queues maintain two data pointers, front and rear. Therefore, its operations are comparatively difficult to implement than that of stacks.

The following steps should be taken to enqueue (insert) data into a queue –

Check if the queue is full.

If the queue is full, produce overflow error and exit.

If the queue is not full, increment rear pointer to point the next empty space.

Add data element to the queue location, where the rear is pointing.

return success.

Algorithm for enqueue operation

procedure enqueue(data)

{ if queue is full

return overflow

end if

rear ← rear + 1

queue[rear] ← data

return true

} end procedure

2. Dequeue

Accessing data from the queue is a process of two tasks − access the data where front is pointing and remove the data after access. The following steps are taken to perform dequeue operation −

Check if the queue is empty.

If the queue is empty, produce underflow error and exit.

If the queue is not empty, access the data where front is pointing.

Increment front pointer to point to the next available data element.

Return success.

Algorithm for dequeue operataion

procedure dequeue

{ if queue is empty

return underflow

end if

data = queue[front]

front ← front + 1

return true

} end procedure

3. Peek

peek()This function helps to see the data at the front of the queue.

Algorithm

begin procedure peek

{

return queue[front]

} end procedure

Example:- int peek()

{

return queue[front];

}

4. Isfull

isfull() if we are using single dimension array for implementation of queue, to check for the rear pointer to reach at MAXSIZE to determine that the queue is full. To maintain the queue in a circular linked-list, the algorithm will differ.

Algorithm

begin procedure isfull

{ if rear equals to MAXSIZE

return true

else

return false

endif

} end procedure

Example :- bool isfull()

{

if(rear == MAXSIZE - 1)

return true;

else

return false;

}

5. Isempty

isempty() If the value of front is less than MIN or 0, it tells that the queue is not yet initialized, hence empty.

Algorithm

begin procedure isempty

if front is less than MIN OR front is greater than rear

return true

else

return false

endif

end procedure

Example:- bool isempty()

{

if(front < 0 || front > rear)

return true:

else

return false;

}

6.5 Circular Queue and its advantage

A more suitable method of representing simple queue which prevents an excessive use of memory is to rearrange the weather Q[1], Q[2]….,Q[n] during a circular fashion with Q[1] following Q[n], this is often called circular queue

In a typical queue arrangement re-buffering problem occurs for every dequeue operation. to unravel this problem by joining the front and rear ends of a queue to form the queue as a circular queue

Circular queue may be a linear arrangement. It follows FIFO principle.

In circular queue the last node is connected back to the primary node to form a circle.

Circular linked list fallow the primary In First Out principle.

Elements are added at the buttocks and therefore the elements are deleted at front of the queue

Both the front and therefore the rear pointers points to the start of the array

It is additionally called as “Ring buffer”.

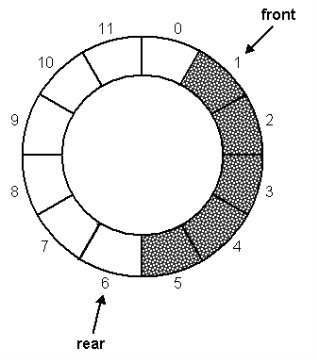
$C:\Users\Kilua Zoldyck\Pictures\r.png$

Figure: -Circular queue

Basic features of Circular Queue

1) In case of a circular queue, head pointer will always point to the front of the queue, and tail pointer will always point to the top of the queue.

2) Initially, the top and therefore the tail pointers are going to be pointing to an equivalent location, this is able to mean that the queue is empty.

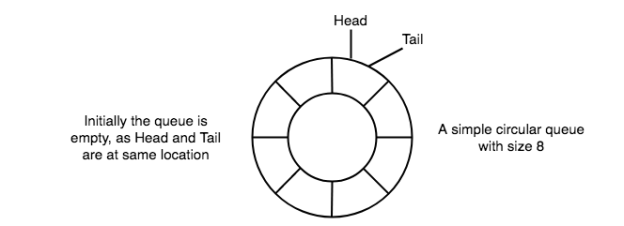
$C:\Users\Kilua Zoldyck\Pictures\2.png$

3) New data is usually added to the situation pointed by the tail pointer, and once the info is added, tail pointer is incremented to point to subsequent available location.

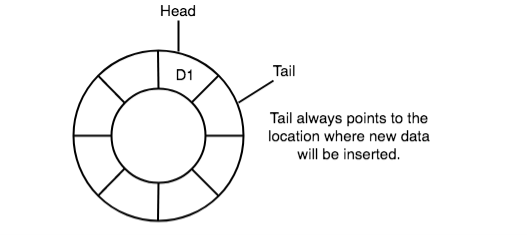
$C:\Users\Kilua Zoldyck\Pictures\3.png$

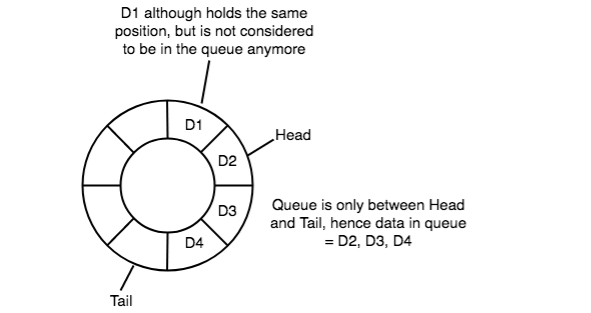
4) In a circular queue, data isn't actually far away from the queue. Only the top pointer is incremented by one position when dequeue is executed. Because the queue data is merely the info between head and tail, hence the info left outside isn't a neighborhood of the queue anymore, hence removed.

$C:\Users\Kilua Zoldyck\Pictures\4.png$

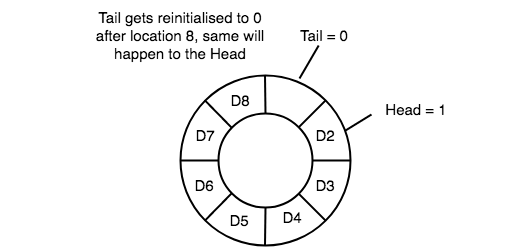
5) The head and therefore the tail pointer will get reinitialized to 0 whenever they reach the top of the queue.

$C:\Users\Kilua Zoldyck\Pictures\5.png$

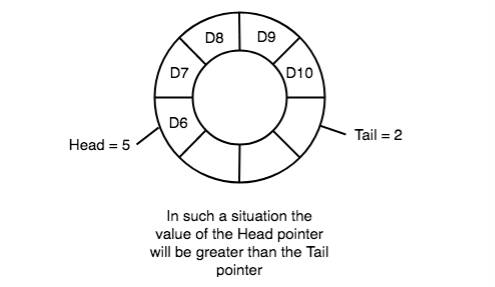
6) Also, the top and therefore the tail pointers can cross one another. In other words, head pointers are often greater than the tail. This may happen once we dequeue the queue a few of times and therefore the tail pointer gets reinitialized upon reaching the top of the queue.

$C:\Users\Kilua Zoldyck\Pictures\6.png$

Implementation of Circular Queue

Steps for implementing circular queue

1) Initialize the queue, with size of the queue defined (maxSize), and head and tail pointers.

2) Enqueue: Check if the amount of elements is adequate to max’Size - 1:

If yes, then return Queue is full.

If No, then add the new data element to the situation of tail pointer and increment the tail pointer.

3) Dequeue: Check if the amount of elements within the queue is zero:

If yes, then return Queue is empty.

If No, then increment the top pointer.

4) Finding the size:

If, tail >= head, size = (tail - head) + 1

But if, head > tail, then size = maxSize - (head - tail) + 1

Applications of Circular queue

Ring Buffers are common data structures frequently used when the input and output to a knowledge stream occur at different rates.

Buffering Data Streams

Computer Controlled Trafficking signal systems

Memory Management

CPU scheduling

Advantages of Circular queue

Circular Queues offer a fast and clean thanks to store FIFO data with a maximum size.

Doesn’t use dynamic memory → No memory leaks

Conserves memory as we only store up to our capacity (opposed to a queue which could still grow if input outpaces output.)

Simple Implementation → easy to trust and test

Never has got to reorganize / copy data around

All operations occur in constant time O(1)

Disadvantages of Circular queue

Circular Queues can only store the pre-determined maximum number of elements.

Have to know the max size beforehand

6.6 Multi-queues

Studies have proven that a single-line queue resulting in multiple servers is more efficient and leads to less variation within the amount of your time customers are kept waiting.

Still, the single-line queue can appear overwhelming customers who fail to know that one longer line is really a far better bet than taking their chances with one among many lines.

Single line queue

Has shorter average wait time. It can appear as if a single-line queue comes with an extended wait, but compared to multiple lines, people are standing in one line for a way shorter time than if that they had chosen from many lines service points are staggered therefore the entire line benefits from one fast cashier and therefore the agony of one slow customer is spread evenly among all who wait.

Promotes fairness. “First come, first served” is inarguably the fairest way for a line to make. When all customers are standing within the same line, the perception is that there's little question who was there when and who should be getting attention before others.

Cuts down on stress. Whether customers are during a rush or not, they stunning much always want to form good use of their time, and this will end in stress about selecting the “right” line. The single-line queue takes away this got to choose.

Reduces jockeying. Line switching is frustrating for patrons and businesses alike. Some people stand and scope out the multiple queues, trying to measure which one is their best bet for getting through the road as quickly as possible. Others pick a line and still rubberneck, seeing if there's a far better option, often jumping from line to line in an attempt to urge through the road faster.

Reduces sweet hearting. one among the foremost common sorts of employee theft, sweet hearting, is when a cashier neglects to scan a couple of items, or only scans the lower-priced items as a prefer to a lover or loved one . During a multiple-line queue, it’s easy for a customer to settle on the road staffed by their acquaintance. During a single-line queue, subsequent person in line has got to report back to subsequent available cashier. This random selection process dramatically reduces sweet hearting.

Multiple line queue

Creates flexibility. The customer has greater flexibility during a multiple-line queue because they get to pick the road during which they need to face. Providing they’re not of the jockeying nature, having the facility to settle on can make a customer happier because they’ve selected where they need to be and aren’t feeling forced to face during a single line.

Deters balking. When there's one line, serpentine or straight, long or short, a customer can feel trapped by the thought of being at the mercy of just one waiting option. Multiple-line queues maintain the illusion that there's more service available and, therefore, well worth the wait.

Implementation of k queues

Create a knowledge structure kQueues that represents k queues. Implementation of kQueues should use just one array, i.e., k queues should use an equivalent array for storing elements. Following functions must be supported by kQueues.

enqueue(int x, int qn) –> adds x to queue number ‘qn’ where qn is from 0 to k-1

dequeue(int qn) –> deletes a component from queue number ‘qn’ where qn is from 0 to k-1

Method 1 (Divide the array in slots of size n/k)

A simple thanks to implement k queues is to divide the array in k slots of size n/k each, and fix the slots for various queues, i.e., use arr[0] to arr[n/k-1] for the primary queue, and arr[n/k] to arr[2n/k-1] for queue2 where arr[] is that the array to be wont to implement two queues and size of array be n.

The problem with this method is an inefficient use of array space. An enqueue operation may end in overflow albeit there's space available in arr[]. For instance , consider k as 2 and array size n as 6. Let we enqueue 3 elements to first and don't enqueue anything to the second queue.

Once we enqueue the 4th element to the primary queue, there'll be overflow albeit we've space for 3 more elements within the array.

Method 2 (A space efficient implementation)

The idea is analogous to the stack post, here we'd like to use three extra arrays. In stack post, we would have liked two extra arrays, another array is required because in queues, enqueue() and dequeue() operations are done at different ends.

Following are the three extra arrays are used:

front[]: this is often of size k and stores indexes of front elements altogether queues.

rear[]: this is often of size k and stores indexes of rear elements altogether queues.

next[]: this is often of size n and stores indexes of next item for all items in array arr[].

Here arr[] is that the actual array that stores k stacks.

Together with k queues, a stack of free slots in arr[] is additionally maintained. The highest of this stack is stored during a variable ‘free’.

All entries in front[] are initialized as -1 to point that each one queues are empty

All entries next[i] are initialized as i+1 because all slots are free initially and pointing to subsequent slot. Top of the free stack, ‘free’ is initialized as 0.

6.7 Linked Queue and Operations

Algorithms for basic primitive operations on queue

1. Insertion at rear

Function: QINSERT_REAR (Q, F, R, N,Y)

Given F and R tips that could the front and rear elements of a queue respectively. Queue Q consisting of N element. This procedure inserts Y at rear end of Queue.

[Overflow]

IF R >= N

2. Then write (‘OVERFLOW’)

Return

[Increment REAR pointer]

R ←R + 1

3. [Insert element ]

Q[R] ←Y

4. [Is front pointer properly set

IF F=0

Then F ←1

Return

2. Deletion from front

Function: QDELETE_FRONT (Q, F, R)

•Given F and R tips that could the front and rear elements of a queue respectively. Queue Q consisting of N element. This function deleted and element from front of the Queue.

[Underflow]

IF F= 0

Then write (‘UNDERFLOW’)

Return (0) (0 denotes an empty Queue)

2. [Decrement element]

Y ←Q[F]

3. [Queue empty?]

IF F=R

Then F←R←0

Else F←F+1 (increment front pointer)

4. [Return element]

Return (Y)

Algorithms for basic primitive operations in Circular Queue

1. Insertion in circular queue

Function: CQINSERT (F, R, Q, N, Y)

Given F and R tips that could the front and rear elements of a circular queue respectively. Circular queue Q consisting of N elements. This procedure inserts Y at buttocks of Circular queue.

[Reset Rear Pointer]

If R = N

Then R← 1

Else R ← R + 1

2. [Overflow]

If F = R

Then Write (‘Overflow’)

Return

3. [Insert element]

Q[R] ← Y

4. [Is front pointer properly set?]

If F = 0

Then F ← 1

Return

2. Deletion in circular queue

Function CQDELETE (F, R, Q, N)

Given F and R tips that could the front and rear elements of a Circular queue respectively. Circular Queue Q consisting of N elements. This function deleted and element from front of the Circular Queue. Y is temporary pointer variable.

[Underflow?]

If F = 0

Then Write (‘UNDERFLOW’)

Return (0)

2. [Delete Element]

Y ← Q[F]

3. [Queue Empty?]

If F = R

Then F ← R ← 0

Return (Y)

4. [Increment front pointer]

If F = N

Then F ← 1

Else F ← F + 1

Return (Y)

Basic primitive operations for DeQueue

1. Insertion in dequeue

Function: -DQINSERT_FRONT (Q, F, R, N,Y)

Given F and R tips that could the front and rear elements of a queue, a queue consisting of N elements and a component Y, this procedure inserts Y at the front of the queue.

[Overflow]

IF F = 0

Then write (‘EMPTY’)

Return

IF F=1

Then write (‘OVERFLOW’)

Return

2. [Decrement front pointer]

F ←F-1

3. [Insert element ]

Q[F] ←Y

Return

2. Deletion in dequeue

Function: DQDELETE_REAR (Q, F, R)

• Given F and R tips that could the front and rear elements of a queue. And a queue Q to which they correspond, this function deletes and returns the last element from the front of a queue. And Y is temporary variable.

[Underflow]

IF R= 0

Then write (‘UNDERFLOW’)

Return (0)

2. [Delete element]

Y ←Q[R]

3. [Queue empty?]

IF R=F

Then R←F←0

Else R←R-1 (decrement front pointer)

4. [Return element]

Return (Y)

Display function in dequeue

Function: - DQUEUE_DISPLAY (F,R,Q)

•Given F and Rare tips that could the front and rear elements of a queue, a queue contains N element. This procedure display Queue contents

[Check for empty]

IF F >= R

Then write (‘QUEUE IS EMPTY’)

Return

2. [Display content]

FOR (I=FRONT; I=REAR;I++)

Write (Q[I])

3. [Return statement]

Return

6.8 Dequeue-Basic concept, types (Input restricted and Output restricted)

A dequeue (double ended queue) may be a linear list during which insertion and deletion are performed from the either end of the structure.

There are two variations of Dequeue

Input restricted dequeue- allows insertion at just one end
Output restricted dequeue- allows deletion from just one end

Such a structure are often represented by following fig.

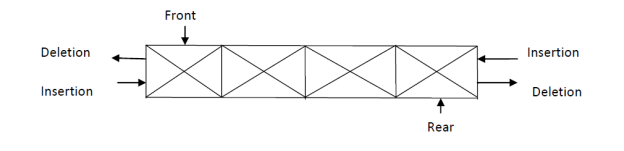
$C:\Users\Kilua Zoldyck\Pictures\3.png$

Double Ended Queue

Double ended queue may be a more generalized sort of queue arrangement which allows insertion and removal of elements from both the ends, i.e , front and back.

The enqueue operation takes place only at the rear, but the dequeue operation takes place at both rear and front

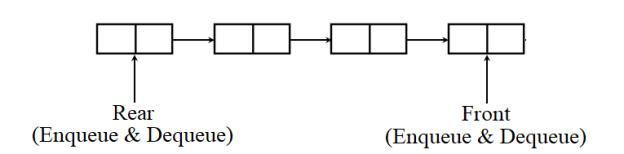
$C:\Users\Kilua Zoldyck\Pictures\d1.png$

An input-restricted queue is useful when we need to remove an item from the rear of the queue

The enqueue operation takes place at both rear and front, but the dequeue operation takes place only at the front:

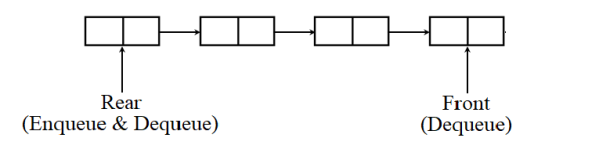
$C:\Users\Kilua Zoldyck\Pictures\d2.png$

An output-restricted queue is handy when we need to insert an item at the front of the queue

Implementation of Double ended Queue

Here we'll implement a double ended queue employing a circular array. It’ll have the subsequent methods:

push_back : inserts element at back

push_front : inserts element at front

pop_back : removes last element

pop_front : removes first element

get_back : returns last element

get_front : returns first element

empty : returns true if queue is empty

full : returns true if queue is full

1. Insert Elements at Front

First we check if the queue is full. If its not full we insert a component at front by following the given conditions

If the queue is empty then intialize front and rear to 0. Both will point to the primary element.

When one element is added- 10

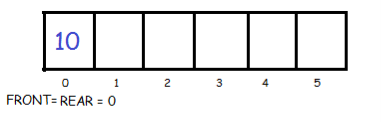
$C:\Users\Kilua Zoldyck\Pictures\q1.png$

Else we decrement front and insert the element. Since we are using circular array, we've to stay in mind that if front is adequate to 0 then rather than decreasing it by 1 we make it adequate to SIZE-1.

Now insert 12 at front

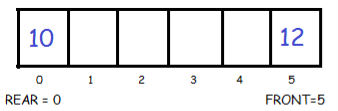
$C:\Users\Kilua Zoldyck\Pictures\q2.png$

Now insert 14 at front

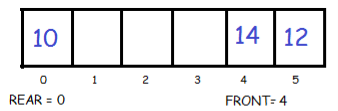
$C:\Users\Kilua Zoldyck\Pictures\q3.png$

2. Insert Elements at back

Again first we check if the queue is full. If it’s not full we insert a component at back by following the given conditions:

If the queue is empty then initialize front and rear to 0. Both will point to the primary element.

Else we increment rear and insert the element. Since we are using circular array, we've to stay in mind that if rear is adequate to SIZE-1 then rather than increasing it by 1 we make it adequate to 0.

Insert 21 at rear

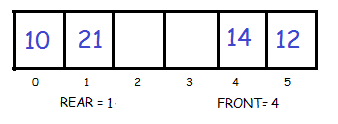
$C:\Users\Kilua Zoldyck\Pictures\q4.png$

3. Delete First Element

In order to try to this, we first check if the queue is empty. If it’s not then delete the front element by following the given conditions :

If just one element is present we once more make front and rear adequate to -1.

Else we increment front. But we've to stay in mind that if front is adequate to SIZE-1 then rather than increasing it by 1 we make it adequate to 0.

Delete from front

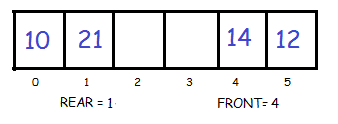
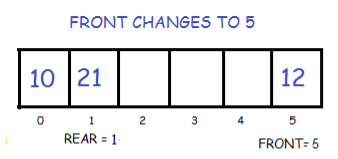
$C:\Users\Kilua Zoldyck\Pictures\q4.png$ $C:\Users\Kilua Zoldyck\Pictures\q6.png$

4. Delete Last Element

In order to try to this, we again first check if the queue is empty. If it’s not then we delete the last element by following the given conditions :

If just one element is present we make front and rear adequate to -1.

Else we decrement rear. But we've to stay in mind that if rear is adequate to 0 then rather than decreasing it by 1 we make it adequate to SIZE-1.

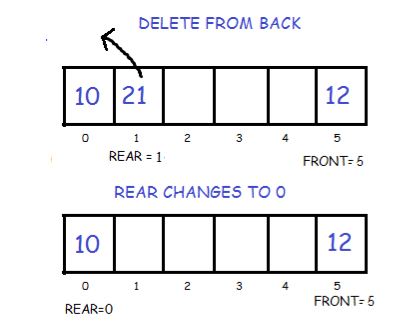
$C:\Users\Kilua Zoldyck\Pictures\q7.png$

6.9 Priority Queue- Basic concept, types (Ascending and Descending).

A priority queue may be a special quite queue during which each item features a predefined priority of service. During this queue, the enqueue operation takes place at the rear within the order of arrival of the things, while the dequeue operation takes place at the front supported the priority of the things.

In a priority queue weareable to insert delete items from any position based on some property (such as giving preference to prior it of the processing task).

An item with a high priority are going to be dequeued before an item with a coffee priority.

Priority Queue is an extension of queue with following properties.

Every item features a priority related to it.

An element with high priority is dequeued before a component with low priority.

If two elements have an equivalent priority, they're served consistent with their order within the queue.

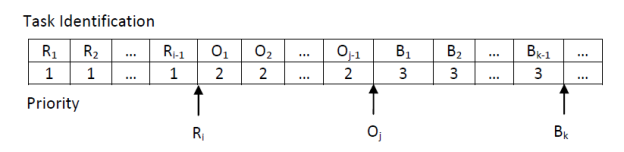$C:\Users\Kilua Zoldyck\Pictures\a.png$ Figure:-Priority Queue viewed as a single queue with insertion allowed at any position

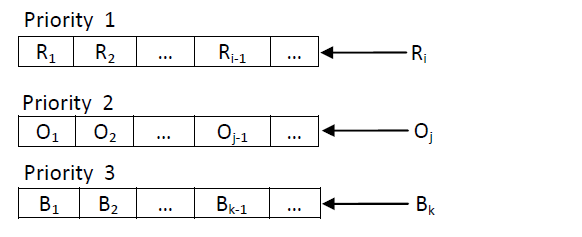
$C:\Users\Kilua Zoldyck\Pictures\b.png$

Figure: - Priority Queue viewed as a Viewed as a set of queue

Priority Queues

Priority queue arrangement is an abstract data type that gives how to take care of a group of elements, each with an associated value called key.

There are two sorts of priority queues: a max-priority queue and a min-priority queue. In both kinds, the priority queue stores a set of elements and is usually ready to provide the foremost “extreme” element, which is that the only due to interact with the priority queue.

Operations

A max-priority queue provides the subsequent operations:

insert: add a component to the priority queue.

maxElement: return the most important element within the priority queue.

removeMaxElement: remove the most important element from the priority queue.

A max-priority queue also can provide these additional operations:

size: return the amount of elements within the priority queue.

increaseKey: updates the key of a component to a bigger value.

updatePriorities: assume the values of the keys are changed and reorder the interior state of the priority queue.

Implementations

1) Unordered array: A simple, yet inefficient implementation, as retrieving the max element would require searching the whole array.

2) Sorted array: This is not a really efficient implementation either. Inserting a replacement element requires linearly searching the array for the right position. Removing similarly requires a linear time: the remainder of the weather got to be adjusted (shifted) into correct positions.

3) Hash table: Although inserting into a hash table takes constant time (given an honest hash function), finding the max element takes linear time. Therefore, this is able to be a poor choice for the underlying arrangement.

4) Heap: It seems that that a heap makes an efficient priority queue.

The complexities of the common operations on a priority queue:

Operations	Unordered array	Sorted array	Hash table	Binary heap
Insert	Θ(1)	Θ(N)	Θ(1)	Θ(log(N))
Max element	Θ(N)	Θ(1)	Θ(N)	Θ(1)
removeMaxElement	Θ(N)	Θ(1)	Θ(N)	Θ(log(N))

ASCENDING-->
Items are entered arbitrarily & only the smallest item may be removed. If apq is an ascending priority queue, the operation pqinsert (apq, x) inserts element x into apq and pqmindelete(apq) removes the minimum element from apq and returns its value.

DESCENDING-->
Items are entered arbitrarily & only the largest item may be removed. A descending priority queue is similar but allows deletion of only the largest item. The operations applicable to a descending priority queue, dpq, are pqinsert(dpq,x) and pqmaxdelete(dpq). pqinsert(dpq,x) inserts an element x into dpq and is logically identical to pqinsert for an ascending priority queue. pqmaxdelete(dpq) removes the maximum element from dpq and returns its value.

Using Heaps-
Heap is generally preferred for priority queue implementation because heaps provide better performance compared arrays or linked list. In a Binary Heap, getHighestPriority() can be implemented in O(1) time, insert() can be implemented in O(Logn) time and deleteHighestPriority() can also be implemented in O(Logn) time.
With Fibonacci heap, insert() and getHighestPriority() can be implemented in O(1) amortized time and deleteHighestPriority() can be implemented in O(Logn) amortized time.

Applications of Priority Queue:

1) CPU Scheduling

2) Graph algorithms like Dijkstra’s shortest path algorithm, Prim’s Minimum Spanning Tree, etc

3) All queue applications where priority is involved

Sign Up

Index

Notes

Highlighted

Underlined

Browse by Topics

Notes

Highlighted

Underlined