UNIT 3

Trees

3.1 Tree – Basic Terminology, General Tree and its Representation

Basic terminology

Static representation of tree

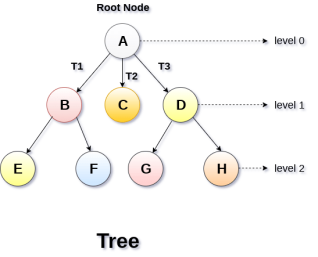
Dynamic representation of tree

Types of Tree

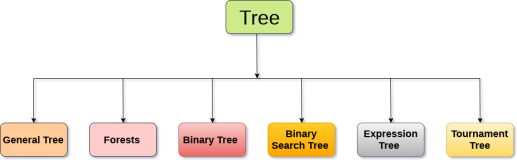
The tree data structure can be classified into six different categories.

General Tree

General Tree stores the elements in a hierarchical order in which the top level element is always present at level 0 as the root element. All the nodes except the root node are present at number of levels. The nodes which are present on the same level are called siblings while the nodes which are present on the different levels exhibit the parent-child relationship among them. A node may contain any number of sub-trees. The tree in which each node contains 3 sub-tree, is called ternary tree.

Forests

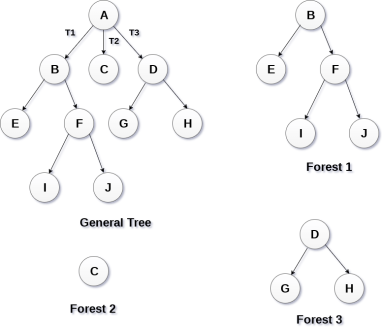
Forest can be defined as the set of disjoint trees which can be obtained by deleting the root node and the edges which connects root node to the first level node.

Binary Tree

Binary tree is a data structure in which each node can have at most 2 children. The node present at the top most level is called the root node. A node with the 0 children is called leaf node. Binary Trees are used in the applications like expression evaluation and many more. We will discuss binary tree in detail, later in this tutorial.

Binary Search Tree

Binary search tree is an ordered binary tree. All the elements in the left sub-tree are less than the root while elements present in the right sub-tree are greater than or equal to the root node element. Binary search trees are used in most of the applications of computer science domain like searching, sorting, etc.

Expression Tree

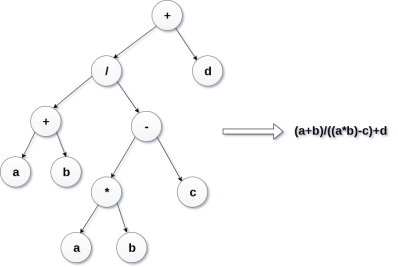
Expression trees are used to evaluate the simple arithmetic expressions. Expression tree is basically a binary tree where internal nodes are represented by operators while the leaf nodes are represented by operands. Expression trees are widely used to solve algebraic expressions like (a+b)*(a-b). Consider the following example.

Q. Construct an expression tree by using the following algebraic expression.

(a + b) / (a*b - c) + d

Tournament Tree

Tournament tree are used to record the winner of the match in each round being played between two players. Tournament tree can also be called as selection tree or winner tree. External nodes represent the players among which a match is being played while the internal nodes represent the winner of the match played. At the top most level, the winner of the tournament is present as the root node of the tree.

For example, tree .of a chess tournament being played among 4 players is shown as follows. However, the winner in the left sub-tree will play against the winner of right sub-tree.

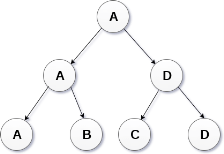
Key takeaway

3.2 Representation using Sequential and Linked Organization

Binary Tree

Binary Tree is a special type of generic tree in which, each node can have at most two children. Binary tree is generally partitioned into three disjoint subsets.

A binary Tree is shown in the following image.

Types of Binary Tree

1. Strictly Binary Tree

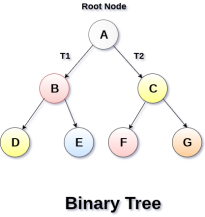
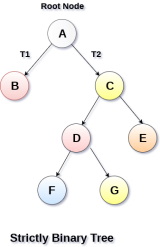
In Strictly Binary Tree, every non-leaf node contains non-empty left and right sub-trees. In other words, the degree of every non-leaf node will always be 2. A strictly binary tree with n leaves, will have (2n - 1) nodes.

A strictly binary tree is shown in the following figure.

2. Complete Binary Tree

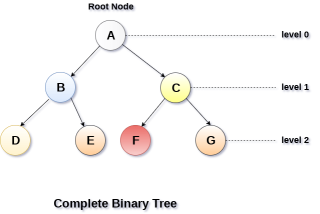
A Binary Tree is said to be a complete binary tree if all of the leaves are located at the same level d. A complete binary tree is a binary tree that contains exactly 2^l nodes at each level between level 0 and d. The total number of nodes in a complete binary tree with depth d is 2d+1-1 where leaf nodes are 2d while non-leaf nodes are 2d-1.

Binary Tree Traversal

Binary Tree representation

There are two types of representation of a binary tree:

1. Linked Representation

In this representation, the binary tree is stored in the memory, in the form of a linked list where the number of nodes are stored at non-contiguous memory locations and linked together by inheriting parent child relationship like a tree. every node contains three parts: pointer to the left node, data element and pointer to the right node. Each binary tree has a root pointer which points to the root node of the binary tree. In an empty binary tree, the root pointer will point to null.

Consider the binary tree given in the figure below.

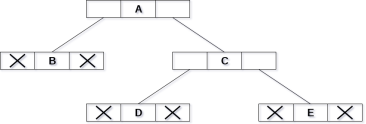
In the above figure, a tree is seen as the collection of nodes where each node contains three parts : left pointer, data element and right pointer. Left pointer stores the address of the left child while the right pointer stores the address of the right child. The leaf node contains null in its left and right pointers.

The following image shows about how the memory will be allocated for the binary tree by using linked representation. There is a special pointer maintained in the memory which points to the root node of the tree. Every node in the tree contains the address of its left and right child. Leaf node contains null in its left and right pointers.

2. Sequential Representation

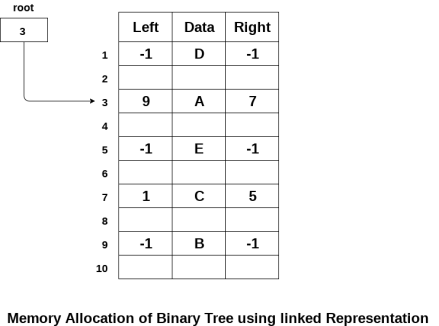
This is the simplest memory allocation technique to store the tree elements but it is an inefficient technique since it requires a lot of space to store the tree elements. A binary tree is shown in the following figure along with its memory allocation.

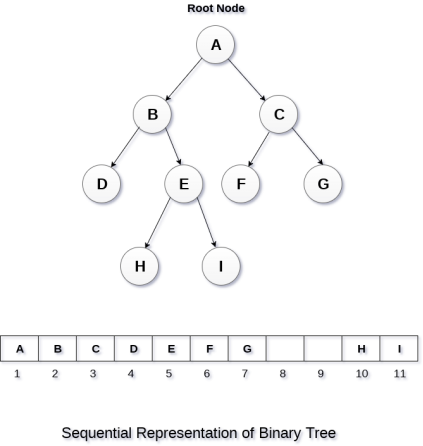
In this representation, an array is used to store the tree elements. Size of the array will be equal to the number of nodes present in the tree. The root node of the tree will be present at the 1st index of the array. If a node is stored at ith index then its left and right children will be stored at 2i and 2i+1 location. If the 1st index of the array i.e. tree[1] is 0, it means that the tree is empty.

Key takeaway

Binary Tree

Binary Tree is a special type of generic tree in which, each node can have at most two children. Binary tree is generally partitioned into three disjoint subsets.

3.3 Binary tree – Properties, Converting Tree to Binary Tree, Binary Tree Traversals (recursive and non-recursive) - Inorder, Preorder, Post Order, Depth First and Breadth First, Operations on Binary Tree

Binary tree is a special type of data structure. In binary tree, every node can have a maximum of 2 children, which are known as Left child and Right Child. It is a method of placing and locating the records in a database, especially when all the data is known to be in random access memory (RAM).

Definition:

"A tree in which every node can have maximum of two children is called as Binary Tree."

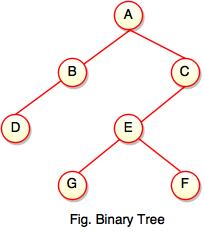
The above tree represents binary tree in which node A has two children B and C. Each child has one child namely D and E respectively.

Binary tree using array represents a node which is numbered sequentially level by level from left to right. Even empty nodes are numbered.

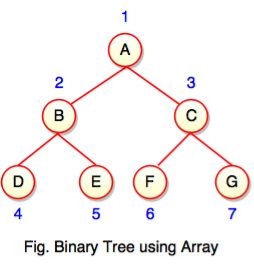
Array index is a value in tree nodes and array value gives to the parent node of that particular index or node. Value of the root node index is always -1 as there is no parent for root. When the data item of the tree is sorted in an array, the number appearing against the node will work as indexes of the node in an array.

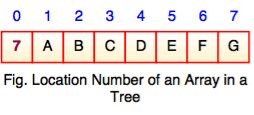
Location number of an array is used to store the size of the tree. The first index of an array that is '0', stores the total number of nodes. All nodes are numbered from left to right level by level from top to bottom. In a tree, each node having an index i is put into the array as its i th element.

The above figure shows how a binary tree is represented as an array. Value '7' is the total number of nodes. If any node does not have any of its child, null value is stored at the corresponding index of the array.

Binary Search Tree

For all nodes A and B,

 

I. If B belongs to the left subtree of A, the key at B is less than the key at A.

II. If B belongs to the right subtree of A, the key at B is greater than the key at A.

Each node has following attributes:

I. Parent (P), left, right which are pointers to the parent (P), left child and right child respectively.

II. Key defines a key which is stored at the node.

Definition:

"Binary Search Tree is a binary tree where each node contains only smaller values in its left subtree and only larger values in its right subtree."

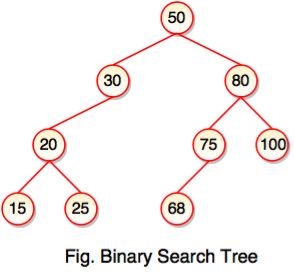
Note: Every binary search tree is a binary tree, but all the binary trees need not to be binary search trees.

Following are the operations performed on binary search tree:

The following algorithm shows the insert operation in binary search tree:

Step 1: Create a new node with a value and set its left and right to NULL.

 
Step 2: Check whether the tree is empty or not.

Step 3: If the tree is empty, set the root to a new node.

 
Step 4: If the tree is not empty, check whether a value of new node is smaller or larger than the node (here it is a root node).

 
Step 5: If a new node is smaller than or equal to the node, move to its left child.

 
Step 6: If a new node is larger than the node, move to its right child.

 
Step 7: Repeat the process until we reach to a leaf node.

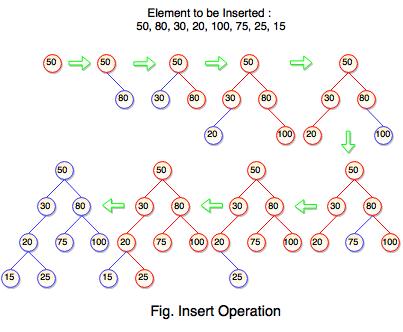
The above tree is constructed a binary search tree by inserting the above elements {50, 80, 30, 20, 100, 75, 25, 15}. The diagram represents how the sequence of numbers or elements are inserted into a binary search tree.

The following algorithm shows the search operation in binary search tree:

Step 1: Read the element from the user.

Step 2: Compare this element with the value of root node in a tree.  

Step 3: If element and value are matching, display "Node is Found" and terminate the function.

Step 4: If element and value are not matching, check whether an element is smaller or larger than a node value.

Step 5: If an element is smaller, continue the search operation in left subtree.  

Step 6: If an element is larger, continue the search operation in right subtree.

Step 7: Repeat the same process until we found the exact element.

Step 8: If an element with search value is found, display "Element is found" and terminate the function.

Step 9: If we reach to a leaf node and the search value is not matched to a leaf node, display "Element is not found" and terminate the function.

Binary tree traversing is a process of accessing every node of the tree and exactly once. A tree is defined in a recursive manner. Binary tree traversal also defined recursively.

There are three techniques of traversal:

1. Preorder Traversal

2. Postorder Traversal

3. Inorder Traversal

Algorithm for preorder traversal

Step 1: Start from the Root.

Step 2: Then, go to the Left Subtree.

Step 3: Then, go to the Right Subtree.

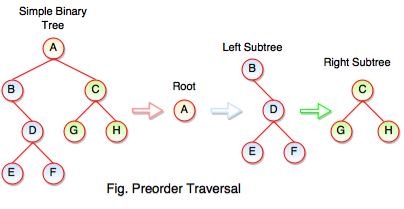
The above figure represents how preorder traversal actually works.

Following steps can be defined the flow of preorder traversal:

Step 1: A + B (B + Preorder on D (D + Preorder on E and F)) + C (C + Preorder on G and H)

Step 2: A + B + D (E + F) + C (G + H)

Step 3: A + B + D + E + F + C + G + H

Preorder Traversal: A B C D E F G H

Algorithm for postorder traversal

Step 1: Start from the Left Subtree (Last Leaf).

Step 2: Then, go to the Right Subtree.

Step 3: Then, go to the Root.

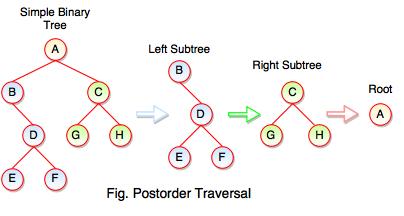
The above figure represents how postorder traversal actually works.

Following steps can be defined the flow of postorder traversal:

Step 1: As we know, preorder traversal starts from left subtree (last leaf) ((Postorder on E + Postorder on F) + D + B )) + ((Postorder on G + Postorder on H) + C) + (Root A)

Step 2: (E + F) + D + B + (G + H) + C + A

Step 3: E + F + D + B + G + H + C + A

Postorder Traversal: E F D B G H C A

Algorithm for inorder traversal

Step 1: Start from the Left Subtree.

Step 2: Then, visit the Root.

Step 3: Then, go to the Right Subtree.

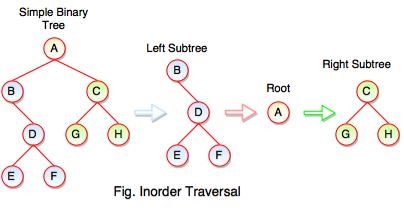
The above figure represents how inorder traversal actually works.

Following steps can be defined the flow of inorder traversal:

Step 1: B + (Inorder on E) + D + (Inorder on F) + (Root A ) + (Inorder on G) + C (Inorder on H)

Step 2: B + (E) + D + (F) + A + G + C + H

Step 3: B + E + D + F + A + G + C + H

Inorder Traversal: B E D F A G C H

#include<stdio.h>
#include<stdlib.h>

struct node  

{  

      int data;  

      struct node *rlink;  

      struct node *llink;  

}*tmp=NULL;  

typedef struct node NODE;  

NODE *create();  

void preorder(NODE *);

void inorder(NODE *);

void postorder(NODE *);

void insert(NODE *);

int main()

{

     int n,i,ch;

     do

     {

          printf("\n\n1.Create\n\n2.Insert\n\n3.Preorder\n\n4.Postorder\n\n5.Inor

er\n\n6.Exit\n\n");
          printf("\n\nEnter Your Choice : ");

          scanf("%d",&ch);

          switch(ch)
          {
               case 1:

                    tmp=create();

                    break;

               case 2:

                    insert(tmp);

                    break;

               case 3:

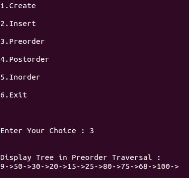
                    printf("\n\nDisplay Tree in Preorder Traversal : ");

                    preorder(tmp);

                    break;

               case 4:

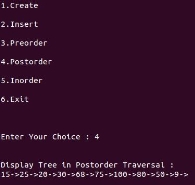
                    printf("\n\nDisplay Tree in Postorder Traversal : ");

                    postorder(tmp);

                    break;

               case 5:

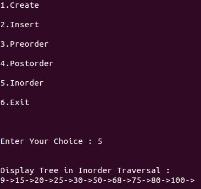
                    printf("\n\nDisplay Tree in Inorder Traversal : ");

                    inorder(tmp);
                    break;
               case 6:

                    exit(0);

                    default:

                    printf("\n Inavild Choice..");

          }
     }
     while(n!=5);
}
void insert(NODE *root)

{
     NODE *newnode;

     if(root==NULL)
     {
          newnode=create();
          root=newnode;
     }
     else
     {
          newnode=create();
          while(1)
          {
               if(newnode->data<root->data)
               {
                    if(root->llink==NULL)
                    {
                         root->llink=newnode;
                         break;
                    }
                    root=root->llink;
               }
               if(newnode->data>root->data)
               {
                    if(root->rlink==NULL)
                    {
                         root->rlink=newnode;
                         break;
                    }
                    root=root->rlink;
               }
          }
     }
}
NODE *create()

{
     NODE *newnode;

     int n;

     newnode=(NODE *)malloc(sizeof(NODE));

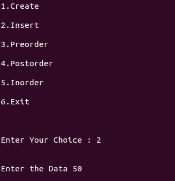
     printf("\n\nEnter the Data ");

     scanf("%d",&n);

     newnode->data=n;

     newnode->llink=NULL;

     newnode->rlink=NULL;

     return(newnode);
}
void postorder(NODE *tmp)

{
     if(tmp!=NULL)
     {
          postorder(tmp->llink);
          postorder(tmp->rlink);
          printf("%d->",tmp->data);
     }
}
void inorder(NODE *tmp)

{
     if(tmp!=NULL)
     {
          inorder(tmp->llink);
          printf("%d->",tmp->data);
          inorder(tmp->rlink);
     }
}
void preorder(NODE *tmp)

{
     if(tmp!=NULL)
     {
          printf("%d->",tmp->data);
          preorder(tmp->llink);
          preorder(tmp->rlink);
     }
}

Output:

1. Create

2. Insert

3. Pre-order Traversal

4. Post-order Traversal

5. In-order Traversal

Key takeaway

Binary tree is a special type of data structure. In binary tree, every node can have a maximum of 2 children, which are known as Left child and Right Child. It is a method of placing and locating the records in a database, especially when all the data is known to be in random access memory (RAM).

Definition:

"A tree in which every node can have maximum of two children is called as Binary Tree."

3.4 Huffman Tree (Concept and Use)

Definition

Huffman coding provides codes to characters such that the length of the code depends on the relative frequency or weight of the corresponding character. Huffman codes are of variable-length, and without any prefix (that means no code is a prefix of any other). Any prefix-free binary code can be displayed or visualized as a binary tree with the encoded characters stored at the leaves.

Huffman tree or Huffman coding tree defines as a full binary tree in which each leaf of the tree corresponds to a letter in the given alphabet.

The Huffman tree is treated as the binary tree associated with minimum external path weight that means, the one associated with the minimum sum of weighted path lengths for the given set of leaves. So the goal is to construct a tree with the minimum external path weight.

An example is given below-

Letter frequency table

Huffman code

The Huffman tree (for the above example) is given below -

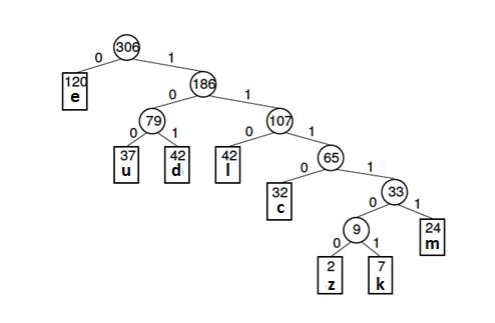
Huffman coding is a lossless data compression algorithm. In this algorithm, a variable-length code is assigned to input different characters. The code length is related to how frequently characters are used. Most frequent characters have the smallest codes and longer codes for least frequent characters.

There are mainly two parts. First one to create a Huffman tree, and another one to traverse the tree to find codes.

For an example, consider some strings “YYYZXXYYX”, the frequency of character Y is larger than X and the character Z has the least frequency. So the length of the code for Y is smaller than X, and code for X will be smaller than Z.

Complexity for assigning the code for each character according to their frequency is O(n log n)

Input and Output

Input:

A string with different characters, say “ACCEBFFFFAAXXBLKE”

Output:

Code for different characters:

Data: K, Frequency: 1, Code: 0000

Data: L, Frequency: 1, Code: 0001

Data: E, Frequency: 2, Code: 001

Data: F, Frequency: 4, Code: 01

Data: B, Frequency: 2, Code: 100

Data: C, Frequency: 2, Code: 101

Data: X, Frequency: 2, Code: 110

Data: A, Frequency: 3, Code: 111

Algorithm

HuffmanCoding(string)

Input: A string with different characters.

Output: The codes for each individual characters.

Begin

   define a node with character, frequency, left and right child of the node for Huffman tree.

   create a list ‘freq’ to store frequency of each character, initially, all are 0

   for each character c in the string do

      increase the frequency for character ch in freq list.

   done

   for all type of character ch do

      if the frequency of ch is non zero then

         add ch and its frequency as a node of priority queue Q.

   done

   while Q is not empty do

      remove item from Q and assign it to left child of node

      remove item from Q and assign to the right child of node

      traverse the node to find the assigned code

   done

End

traverseNode(n: node, code)

Input: The node n of the Huffman tree, and the code assigned from the previous call

Output: Code assigned with each character

if a left child of node n ≠φ then

   traverseNode(leftChild(n), code+’0’)     //traverse through the left child

   traverseNode(rightChild(n), code+’1’)    //traverse through the right child

else

   display the character and data of current node.

Example

#include

#include

#include

using namespace std;

struct node {

   int freq;

   char data;

   const node *child0, *child1;

   node(char d, int f = -1) { //assign values in the node

      data = d;

      freq = f;

      child0 = NULL;

      child1 = NULL;

   }

   node(const node *c0, const node *c1) {

      data = 0;

      freq = c0->freq + c1->freq;

      child0=c0;

      child1=c1;

   }

   bool operator<( const node &a ) const { //< operator performs to find priority in queue

      return freq >a.freq;

   }

   void traverse(string code = "")const {

      if(child0!=NULL) {

         child0->traverse(code+'0'); //add 0 with the code as left child

         child1->traverse(code+'1'); //add 1 with the code as right child

      }else {

         cout << "Data: " << data<< ", Frequency: "< qu;

   int frequency[256];

   for(int i = 0; i<256; i++)

      frequency[i] = 0; //clear all frequency

   for(int i = 0; i1) {

      node *c0 = new node(qu.top()); //get left child and remove from queue

      qu.pop();

      node *c1 = new node(qu.top()); //get right child and remove from queue

      qu.pop();

      qu.push(node(c0, c1)); //add freq of two child and add again in the queue

   }

   cout << "The Huffman Code: "<

Output

The Huffman Code:

Data: K, Frequency: 1, Code: 0000

Data: L, Frequency: 1, Code: 0001

Data: E, Frequency: 2, Code: 001

Data: F, Frequency: 4, Code: 01

Data: B, Frequency: 2, Code: 100

Data: C, Frequency: 2, Code: 101

Data: X, Frequency: 2, Code: 110

Data: A, Frequency: 3, Code: 111

Key takeaway

Definition

Huffman coding provides codes to characters such that the length of the code depends on the relative frequency or weight of the corresponding character. Huffman codes are of variable-length, and without any prefix (that means no code is a prefix of any other). Any prefix-free binary code can be displayed or visualized as a binary tree with the encoded characters stored at the leaves.

Huffman tree or Huffman coding tree defines as a full binary tree in which each leaf of the tree corresponds to a letter in the given alphabet.

The Huffman tree is treated as the binary tree associated with minimum external path weight that means, the one associated with the minimum sum of weighted path lengths for the given set of leaves. So the goal is to construct a tree with the minimum external path weight.

3.5 Binary Search Tree (BST), BST operations

Binary Search Tree

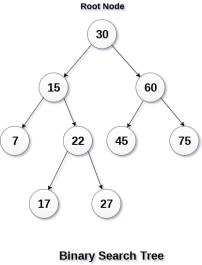
A Binary search tree is shown in the above figure. As the constraint applied on the BST, we can see that the root node 30 doesn't contain any value greater than or equal to 30 in its left sub-tree and it also doesn't contain any value less than 30 in its right sub-tree.

Advantages of using binary search tree

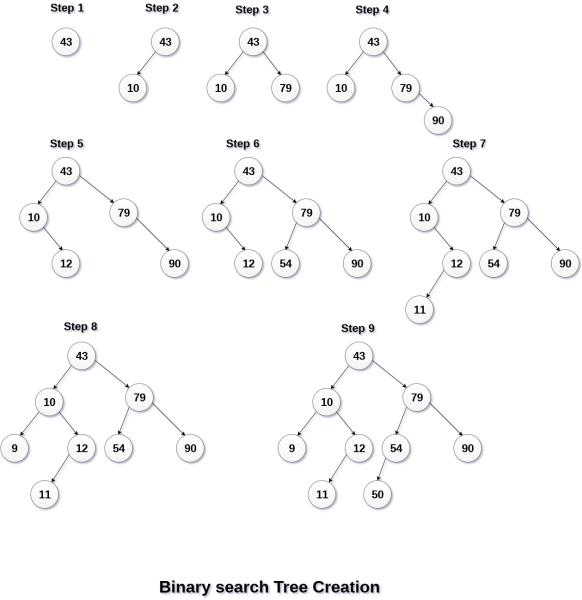
Q. Create the binary search tree using the following data elements.

43, 10, 79, 90, 12, 54, 11, 9, 50

The process of creating BST by using the given elements, is shown in the image below.

Operations on Binary Search Tree

There are many operations which can be performed on a binary search tree.

Program to implement BST operations

Output:

Enter value to be inserted? 10

Enter value to be inserted? 20

Enter value to be inserted? 30

Enter value to be inserted? 40

Enter value to be inserted?  5

Enter value to be inserted? 25

Enter value to be inserted? 15

Enter value to be inserted?  5

5 5 10 15 20 25 30 40 

5 5 15 20 25 30 40 

Searching

Searching means finding or locating some specific element or node within a data structure. However, searching for some specific node in binary search tree is pretty easy due to the fact that, element in BST are stored in a particular order.

Algorithm:

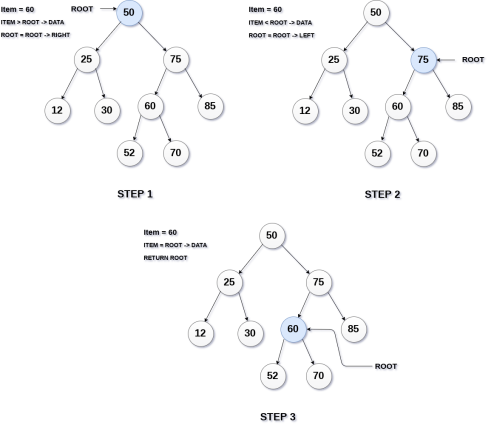
Search (ROOT, ITEM)

    Return ROOT

   ELSE

   IF ROOT < ROOT -> DATA

   Return search(ROOT -> LEFT, ITEM)

  ELSE

   Return search(ROOT -> RIGHT,ITEM)

  [END OF IF]

  [END OF IF]

Insertion

Insert function is used to add a new element in a binary search tree at appropriate location. Insert function is to be designed in such a way that, it must node violate the property of binary search tree at each value.

Insert (TREE, ITEM)

C Function

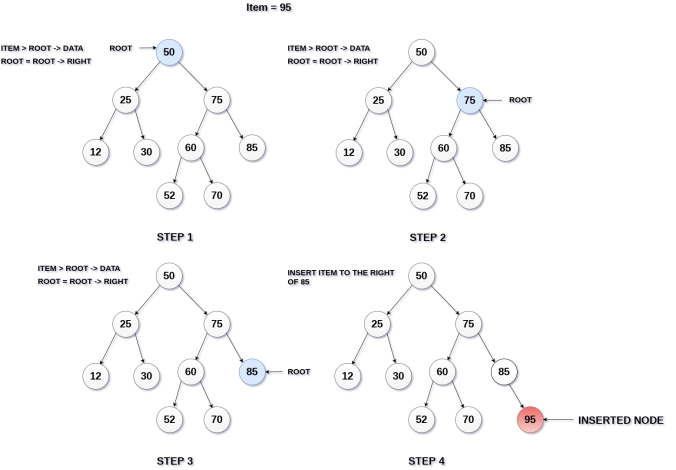
Output

Enter the item which you want to insert?

12

Node Inserted

Press 0 to insert more?

0

Enter the item which you want to insert?

23

Node Inserted

Press 0 to insert more?

1

Deletion

Delete function is used to delete the specified node from a binary search tree. However, we must delete a node from a binary search tree in such a way, that the property of binary search tree doesn't violate. There are three situations of deleting a node from binary search tree.

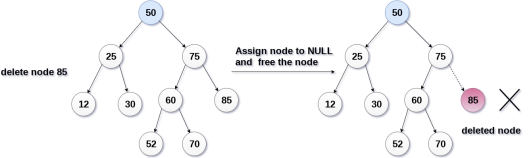
The node to be deleted is a leaf node

It is the simplest case, in this case, replace the leaf node with the NULL and simple free the allocated space.

In the following image, we are deleting the node 85, since the node is a leaf node, therefore the node will be replaced with NULL and allocated space will be freed.

The node to be deleted has only one child.

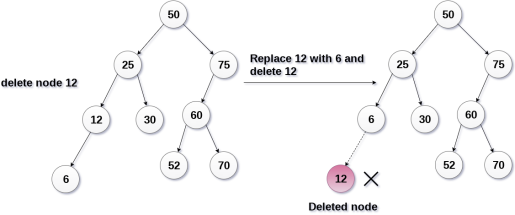
In this case, replace the node with its child and delete the child node, which now contains the value which is to be deleted. Simply replace it with the NULL and free the allocated space.

In the following image, the node 12 is to be deleted. It has only one child. The node will be replaced with its child node and the replaced node 12 (which is now leaf node) will simply be deleted.

The node to be deleted has two children.

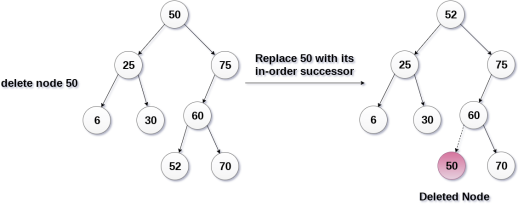
It is a bit complexed case compare to other two cases. However, the node which is to be deleted, is replaced with its in-order successor or predecessor recursively until the node value (to be deleted) is placed on the leaf of the tree. After the procedure, replace the node with NULL and free the allocated space.

In the following image, the node 50 is to be deleted which is the root node of the tree. The in-order traversal of the tree given below.

6, 25, 30, 50, 52, 60, 70, 75.

replace 50 with its in-order successor 52. Now, 50 will be moved to the leaf of the tree, which will simply be deleted.

Algorithm

Delete (TREE, ITEM)

Function:

Key takeaway

Binary Search Tree

3.6 Threaded Binary Search Tree – Concepts, Threading, Insertion and Deletion of Nodes in Inorder Threaded Binary Search Tree, In Order Traversal of In-order Threaded Binary Search Tree

Here we will see the threaded binary tree data structure. We know that the binary tree nodes may have at most two children. But if they have only one children, or no children, the link part in the linked list representation remains null. Using threaded binary tree representation, we can reuse that empty links by making some threads.

If one node has some vacant left or right child area, that will be used as thread. There are two types of threaded binary tree. The single threaded tree or fully threaded binary tree. In single threaded mode, there are another two variations. Left threaded and right threaded.

In the left threaded mode if some node has no left child, then the left pointer will point to its inorder predecessor, similarly in the right threaded mode if some node has no right child, then the right pointer will point to its inorder successor. In both cases, if no successor or predecessor is present, then it will point to header node.

For fully threaded binary tree, each node has five fields. Three fields like normal binary tree node, another two fields to store Boolean value to denote whether link of that side is actual link or thread.

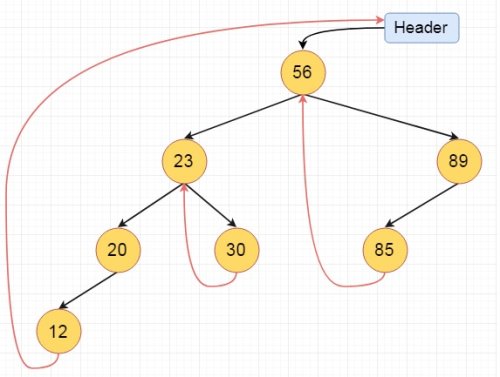
These are the examples of left and right threaded tree

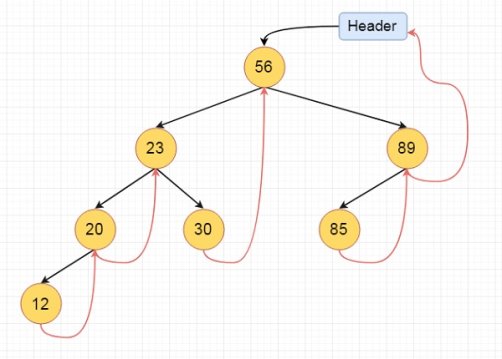
This is the fully threaded binary tree

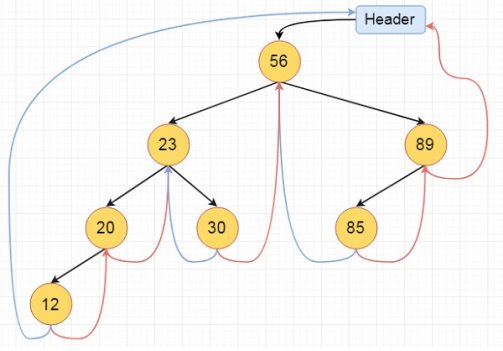
Inorder Traversal of a Threaded Binary Tree

Here we will see the threaded binary tree data structure. We know that the binary tree nodes may have at most two children. But if they have only one children, or no children, the link part in the linked list representation remains null. Using threaded binary tree representation, we can reuse that empty links by making some threads.

If one node has some vacant left or right child area, that will be used as thread. There are two types of threaded binary tree. The single threaded tree or fully threaded binary tree.

For fully threaded binary tree, each node has five fields. Three fields like normal binary tree node, another two fields to store Boolean value to denote whether link of that side is actual link or thread.

This is the fully threaded binary tree

Algorithm

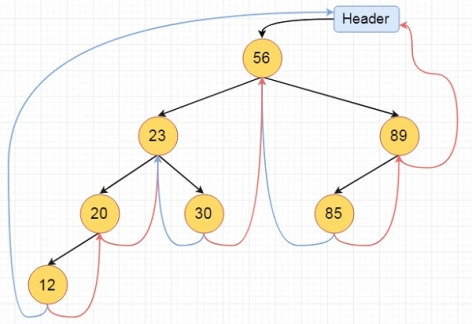
inorder():

Begin

   temp := root

   repeat infinitely, do

   p := temp

   temp = right of temp

   if right flag of p is false, then

      while left flag of temp is not null, do

         temp := left of temp

      done

   end if

   if temp and root are same, then

      break

   end if

      print key of temp

   done

End

Example

#include <iostream>

#define MAX_VALUE 65536

using namespace std;

class N { //node declaration

   public:

      int k;

      N *l, *r;

      bool leftTh, rightTh;

};

class ThreadedBinaryTree {

   private:

   N *root;

   public:

   ThreadedBinaryTree() { //constructor to initialize the variables

      root= new N();

      root->r= root->l= root;

      root->leftTh = true;

      root->k = MAX_VALUE;

   }

   void insert(int key) {

      N *p = root;

      for (;;) {

      if (p->k< key) { //move to right thread

         if (p->rightTh)

            break;

         p = p->r;

      }

      else if (p->k > key) { // move to left thread

         if (p->leftTh)

            break;

         p = p->l;

      }

      else {

         return;

      }

   }

   N *temp = new N();

   temp->k = key;

   temp->rightTh= temp->leftTh= true;

   if (p->k < key) {

      temp->r = p->r;

      temp->l= p;

      p->r = temp;

      p->rightTh= false;

   }

   else {

      temp->r = p;

      temp->l = p->l;

      p->l = temp;

      p->leftTh = false;

   }

}

void inorder() { //print the tree

   N *temp = root, *p;

   for (;;) {

      p = temp;

      temp = temp->r;

      if (!p->rightTh) {

         while (!temp->leftTh) {

            temp = temp->l;

         }

      }

      if (temp == root)

         break;

         cout<<temp->k<<" ";

      }

      cout<<endl;

   }

};

int main() {

   ThreadedBinaryTree tbt;

   cout<<"Threaded Binary Tree\n";

   tbt.insert(56);

   tbt.insert(23);

   tbt.insert(89);

   tbt.insert(85);

   tbt.insert(20);

   tbt.insert(30);

   tbt.insert(12);

   tbt.inorder();