A multiway tree is a tree that can have more than two children. A multiway tree of order m (or an m-way tree) is one in which a tree can have m children.
As with the other trees that have been studied, the nodes in an m-way tree will be made up of key fields, in this case m-1 key fields, and pointers to children.
multiway tree of order 5
To make the processing of m-way trees easier some type of order will be imposed on the keys within each node, resulting in a multiway search tree of order m (or an m-way search tree). By definition an m-way search tree is a m-way tree in which:
4-way search tree
M-way search trees give the same advantages to m-way trees that binary search trees gave to binary trees - they provide fast information retrieval and update. However, they also have the same problems that binary search trees had - they can become unbalanced, which means that the construction of the tree becomes of vital importance.
An extension of a multiway search tree of order m is a B-tree of order m. This type of tree will be used when the data to be accessed/stored is located on secondary storage devices because they allow for large amounts of data to be stored in a node.
A B-tree of order m is a multiway search tree in which:
These restrictions make B-trees always at least half full, have few levels, and remain perfectly balanced.
The nodes in a B-tree are usually implemented as a class that contains an array of m-l cells for keys, an array of m pointers to other nodes, and whatever other information is required in order to facilitate tree maintenance.
template <class T, int M>
class BTreeNode
{
public:
BTreeNode();
BTreeNode( const T & );
private:
T keys[M-1];
BTreeNode *pointers[M];
...
};
An algorithm for finding a key in B-tree is simple. Start at the root and determine which pointer to follow based on a comparison between the search value and key fields in the root node. Follow the appropriate pointer to a child node. Examine the key fields in the child node and continue to follow the appropriate pointers until the search value is found or a leaf node is reached that doesn't contain the desired search value.
The condition that all leaves must be on the same level forces a characteristic behavior of B-trees, namely that B-trees are not allowed to grow at the their leaves; instead they are forced to grow at the root.
When inserting into a B-tree, a value is inserted directly into a leaf. This leads to three common situations that can occur:
Case 1: A key is placed into a leaf that still has room
This is the easiest of the cases to solve because the value is simply inserted into the correct sorted position in the leaf node.
Inserting the number 7 results in:
Case 2: The leaf in which a key is to be placed is full
In this case, the leaf node where the value should be inserted is split in two, resulting in a new leaf node. Half of the keys will be moved from the full leaf to the new leaf. The new leaf is then incorporated into the B-tree.
The new leaf is incorporated by moving the middle value to the parent and a pointer to the new leaf is also added to the parent. This process is continues up the tree until all of the values have "found" a location.
Insert 6 into the following B-tree:
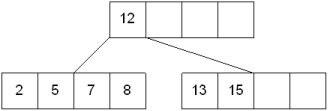
results in a split of the first leaf node:
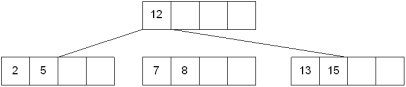
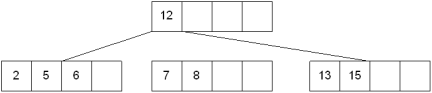
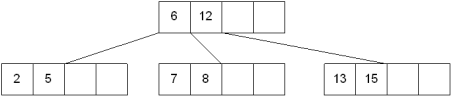
The new node needs to be incorporated into the tree - this is accomplished by taking the middle value and inserting it in the parent:
Case 3: The root of the B-tree is full
The upward movement of values from case 2 means that it's possible that a value could move up to the root of the B-tree. If the root is full, the same basic process from case 2 will be applied and a new root will be created. This type of split results in 2 new nodes being added to the B-tree.
Inserting 13 into the following tree:

Results in:

The 15 needs to be moved to the root node but it is full. This means that the root needs to be divided:

The 15 is inserted into the parent, which means that it becomes the new root node:

As usual, this is the hardest of the processes to apply. The deletion process will basically be a reversal of the insertion process - rather than splitting nodes, it's possible that nodes will be merged so that B-tree properties, namely the requirement that a node must be at least half full, can be maintained.
There are two main cases to be considered:
Case 1: Deletion from a leaf
1a) If the leaf is at least half full after deleting the desired value, the remaining larger values are moved to "fill the gap".
Deleting 6 from the following tree:

results in:

1b) If the leaf is less than half full after deleting the desired value (known as underflow), two things could happen:
Deleting 7 from the tree above results in:

1b-1) If there is a left or right sibling with the number of keys exceeding the minimum requirement, all of the keys from the leaf and sibling will be redistributed between them by moving the separator key from the parent to the leaf and moving the middle key from the node and the sibling combined to the parent.

Now delete 8 from the tree:

1b-2) If the number of keys in the sibling does not exceed the minimum requirement, then the leaf and sibling are merged by putting the keys from the leaf, the sibling, and the separator from the parent into the leaf. The sibling node is discarded and the keys in the parent are moved to "fill the gap". It's possible that this will cause the parent to underflow. If that is the case, treat the parent as a leaf and continue repeating step 1b-2 until the minimum requirement is met or the root of the tree is reached.
Special Case for 1b-2: When merging nodes, if the parent is the root with only one key, the keys from the node, the sibling, and the only key of the root are placed into a node and this will become the new root for the B-tree. Both the sibling and the old root will be discarded.


Case 2: Deletion from a non-leaf
This case can lead to problems with tree reorganization but it will be solved in a manner similar to deletion from a binary search tree.
The key to be deleted will be replaced by its immediate predecessor (or successor) and then the predecessor (or successor) will be deleted since it can only be found in a leaf node.
Deleting 16 from the tree above results in:

The "gap" is filled in with the immediate predecessor:

and then the immediate predecessor is deleted:

If the immediate successor had been chosen as the replacement:

Deleting the successor results in:

The vales in the left sibling are combined with the separator key (18) and the remaining values. They are divided between the 2 nodes:

and then the middle value is moved to the parent:

Indexing
We know that data is stored in the form of records. Every record has a key field, which helps it to be recognized uniquely.
Indexing is a data structure technique to efficiently retrieve records from the database files based on some attributes on which the indexing has been done. Indexing in database systems is similar to what we see in books.
Indexing is defined based on its indexing attributes. Indexing can be of the following types −
Ordered Indexing is of two types −
In dense index, there is an index record for every search key value in the database. This makes searching faster but requires more space to store index records itself. Index records contain search key value and a pointer to the actual record on the disk.
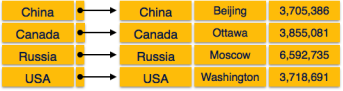
In sparse index, index records are not created for every search key. An index record here contains a search key and an actual pointer to the data on the disk. To search a record, we first proceed by index record and reach at the actual location of the data. If the data we are looking for is not where we directly reach by following the index, then the system starts sequential search until the desired data is found.
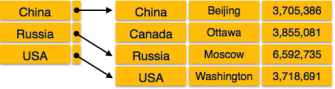
Index records comprise search-key values and data pointers. Multilevel index is stored on the disk along with the actual database files. As the size of the database grows, so does the size of the indices. There is an immense need to keep the index records in the main memory so as to speed up the search operations. If single-level index is used, then a large size index cannot be kept in memory which leads to multiple disk accesses.
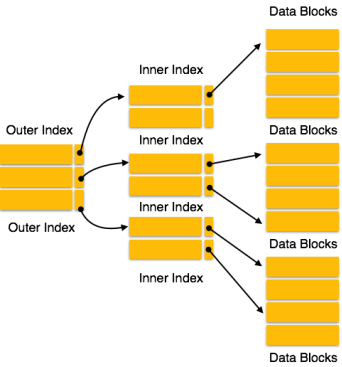
Multi-level Index helps in breaking down the index into several smaller indices in order to make the outermost level so small that it can be saved in a single disk block, which can easily be accommodated anywhere in the main memory.
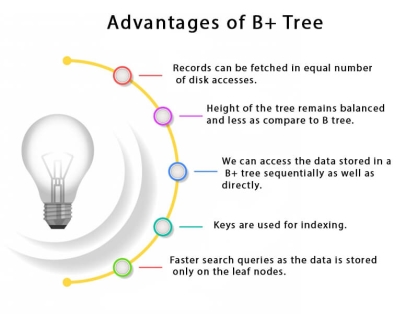
A B+ tree is a balanced binary search tree that follows a multi-level index format. The leaf nodes of a B+ tree denote actual data pointers. B+ tree ensures that all leaf nodes remain at the same height, thus balanced. Additionally, the leaf nodes are linked using a link list; therefore, a B+ tree can support random access as well as sequential access.
Every leaf node is at equal distance from the root node. A B+ tree is of the order n where n is fixed for every B+ tree.
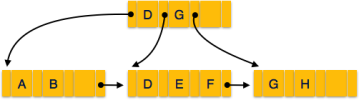
Internal nodes −
Leaf nodes −
- Split node into two parts.
- Partition at i = ⌊(m+1)/2⌋.
- First i entries are stored in one node.
- Rest of the entries (i+1 onwards) are moved to a new node.
- ith key is duplicated at the parent of the leaf.
- Split node into two parts.
- Partition the node at i = ⌈(m+1)/2⌉.
- Entries up to i are kept in one node.
- Rest of the entries are moved to a new node.
- If it is an internal node, delete and replace with the entry from the left position.
- If underflow occurs, distribute the entries from the nodes left to it.
- Distribute from the nodes right to it.
- Merge the node with left and right to it.
Key takeaway
A multiway tree is a tree that can have more than two children. A multiway tree of order m (or an m-way tree) is one in which a tree can have m children.
As with the other trees that have been studied, the nodes in an m-way tree will be made up of key fields, in this case m-1 key fields, and pointers to children.
The m-way search trees are multi-way trees which are generalised versions of binary trees here each node contains multiple elements. In an m-Way tree of order m, each node contains a maximum of m – 1 elements and m children.
The goal of m-Way search tree of height h calls for O(h) no. of accesses for an insert/delete/retrieval operation. Hence, it ensures that the height h is close to log_m(n + 1).
The number of elements in an m-Way search tree of height h ranges from a minimum of h to a maximum of  .
.
An m-Way search tree of n elements ranges from a minimum height of log_m(n+1) to a maximum of n
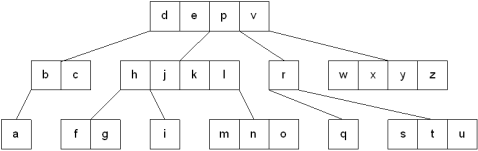
An example of a 5-Way search tree is shown in the figure below. Observe how each node has at most 5 child nodes & therefore has at most 4 keys contained in it.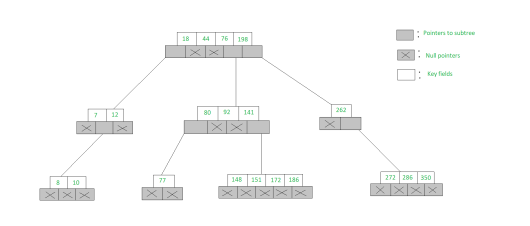
The structure of a node of an m-Way tree is given below:
struct node { int count; int value[MAX + 1]; struct node* child[MAX + 1]; }; |
Searching in an m-Way search tree:
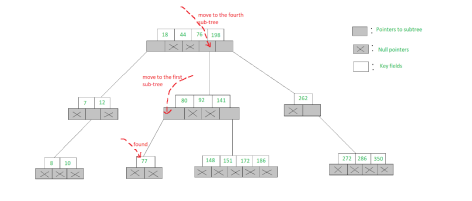
// Searches value in the node struct node* search(int val, struct node* root, int* pos) {
// if root is Null then return if (root == NULL) return NULL; else {
// if node is found if (searchnode(val, root, pos)) return root;
// if not then search in child nodes else return search(val, root->child[*pos], pos); } }
// Searches the node int searchnode(int val, struct node* n, int* pos) { // if val is less than node->value[1] if (val < n->value[1]) { *pos = 0; return 0; }
// if the val is greater else { *pos = n->count;
// check in the child array // for correct position while ((val < n->value[*pos]) && *pos > 1) (*pos)--; if (val == n->value[*pos]) return 1; else return 0; } } |
search():
searchnode():
Key takeaway
The m-way search trees are multi-way trees which are generalised versions of binary trees here each node contains multiple elements. In an m-Way tree of order m, each node contains a maximum of m – 1 elements and m children.
The goal of m-Way search tree of height h calls for O(h) no. of accesses for an insert/delete/retrieval operation. Hence, it ensures that the height h is close to log_m(n + 1).
The number of elements in an m-Way search tree of height h ranges from a minimum of h to a maximum of  .
.
An m-Way search tree of n elements ranges from a minimum height of log_m(n+1) to a maximum of n
B Tree is a specialized m-way tree that can be widely used for disk access. A B-Tree of order m can have at most m-1 keys and m children. One of the main reasons of using B tree is its capability to store large number of keys in a single node and large key values by keeping the height of the tree relatively small.
A B tree of order m contains all the properties of an M way tree. In addition, it contains the following properties.
It is not necessary that, all the nodes contain the same number of children but, each node must have m/2 number of nodes.
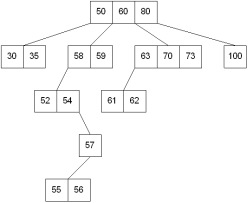
A B tree of order 4 is shown in the following image.
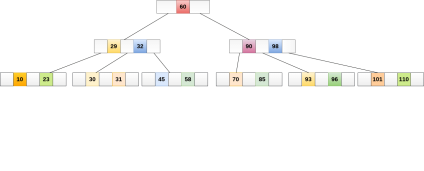
While performing some operations on B Tree, any property of B Tree may violate such as number of minimum children a node can have. To maintain the properties of B Tree, the tree may split or join.
Searching in B Trees is similar to that in Binary search tree. For example, if we search for an item 49 in the following B Tree. The process will something like following:
Searching in a B tree depends upon the height of the tree. The search algorithm takes O(log n) time to search any element in a B tree.
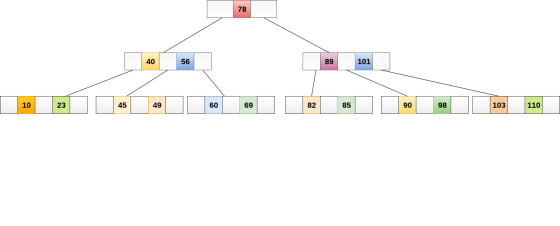
Insertions are done at the leaf node level. The following algorithm needs to be followed in order to insert an item into B Tree.
- Insert the new element in the increasing order of elements.
- Split the node into the two nodes at the median.
- Push the median element upto its parent node.
- If the parent node also contain m-1 number of keys, then split it too by following the same steps.
Example:
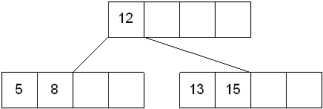
Insert the node 8 into the B Tree of order 5 shown in the following image.

8 will be inserted to the right of 5, therefore insert 8.

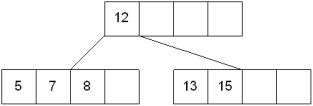
The node, now contain 5 keys which is greater than (5 -1 = 4 ) keys. Therefore split the node from the median i.e. 8 and push it up to its parent node shown as follows.

Deletion is also performed at the leaf nodes. The node which is to be deleted can either be a leaf node or an internal node. Following algorithm needs to be followed in order to delete a node from a B tree.
- If the left sibling contains more than m/2 elements then push its largest element up to its parent and move the intervening element down to the node where the key is deleted.
- If the right sibling contains more than m/2 elements then push its smallest element up to the parent and move intervening element down to the node where the key is deleted.
If the the node which is to be deleted is an internal node, then replace the node with its in-order successor or predecessor. Since, successor or predecessor will always be on the leaf node hence, the process will be similar as the node is being deleted from the leaf node.
Example 1
Delete the node 53 from the B Tree of order 5 shown in the following figure.

53 is present in the right child of element 49. Delete it.

Now, 57 is the only element which is left in the node, the minimum number of elements that must be present in a B tree of order 5, is 2. it is less than that, the elements in its left and right sub-tree are also not sufficient therefore, merge it with the left sibling and intervening element of parent i.e. 49.
The final B tree is shown as follows.

B tree is used to index the data and provides fast access to the actual data stored on the disks since, the access to value stored in a large database that is stored on a disk is a very time consuming process.
Searching an un-indexed and unsorted database containing n key values needs O(n) running time in worst case. However, if we use B Tree to index this database, it will be searched in O(log n) time in worst case.
Key takeaway
B Tree is a specialized m-way tree that can be widely used for disk access. A B-Tree of order m can have at most m-1 keys and m children. One of the main reasons of using B tree is its capability to store large number of keys in a single node and large key values by keeping the height of the tree relatively small.
A B tree of order m contains all the properties of an M way tree. In addition, it contains the following properties.
B+ Tree is an extension of B Tree which allows efficient insertion, deletion and search operations.
In B Tree, Keys and records both can be stored in the internal as well as leaf nodes. Whereas, in B+ tree, records (data) can only be stored on the leaf nodes while internal nodes can only store the key values.
The leaf nodes of a B+ tree are linked together in the form of a singly linked lists to make the search queries more efficient.
B+ Tree are used to store the large amount of data which can not be stored in the main memory. Due to the fact that, size of main memory is always limited, the internal nodes (keys to access records) of the B+ tree are stored in the main memory whereas, leaf nodes are stored in the secondary memory.
The internal nodes of B+ tree are often called index nodes. A B+ tree of order 3 is shown in the following figure.

SN | B Tree | B+ Tree |
1 | Search keys can not be repeatedly stored. | Redundant search keys can be present. |
2 | Data can be stored in leaf nodes as well as internal nodes | Data can only be stored on the leaf nodes. |
3 | Searching for some data is a slower process since data can be found on internal nodes as well as on the leaf nodes. | Searching is comparatively faster as data can only be found on the leaf nodes. |
4 | Deletion of internal nodes are so complicated and time consuming. | Deletion will never be a complexed process since element will always be deleted from the leaf nodes. |
5 | Leaf nodes can not be linked together. | Leaf nodes are linked together to make the search operations more efficient. |
Step 1: Insert the new node as a leaf node
Step 2: If the leaf doesn't have required space, split the node and copy the middle node to the next index node.
Step 3: If the index node doesn't have required space, split the node and copy the middle element to the next index page.
Insert the value 195 into the B+ tree of order 5 shown in the following figure.

195 will be inserted in the right sub-tree of 120 after 190. Insert it at the desired position.

The node contains greater than the maximum number of elements i.e. 4, therefore split it and place the median node up to the parent.

Now, the index node contains 6 children and 5 keys which violates the B+ tree properties, therefore we need to split it, shown as follows.

Step 1: Delete the key and data from the leaves.
Step 2: if the leaf node contains less than minimum number of elements, merge down the node with its sibling and delete the key in between them.
Step 3: if the index node contains less than minimum number of elements, merge the node with the sibling and move down the key in between them.
Delete the key 200 from the B+ Tree shown in the following figure.

200 is present in the right sub-tree of 190, after 195. delete it.

Merge the two nodes by using 195, 190, 154 and 129.

Now, element 120 is the single element present in the node which is violating the B+ Tree properties. Therefore, we need to merge it by using 60, 78, 108 and 120.
Now, the height of B+ tree will be decreased by 1.

Key takeaway
B+ Tree is an extension of B Tree which allows efficient insertion, deletion and search operations.
In B Tree, Keys and records both can be stored in the internal as well as leaf nodes. Whereas, in B+ tree, records (data) can only be stored on the leaf nodes while internal nodes can only store the key values.
The leaf nodes of a B+ tree are linked together in the form of a singly linked lists to make the search queries more efficient.
B+ Tree are used to store the large amount of data which can not be stored in the main memory. Due to the fact that, size of main memory is always limited, the internal nodes (keys to access records) of the B+ tree are stored in the main memory whereas, leaf nodes are stored in the secondary memory.
Trie is an efficient information reTrieval data structure. Using Trie, search complexities can be brought to optimal limit (key length). If we store keys in binary search tree, a well-balanced BST will need time proportional to M * log N, where M is maximum string length and N is number of keys in tree. Using Trie, we can search the key in O(M) time. However the penalty is on Trie storage requirements
Every node of Trie consists of multiple branches. Each branch represents a possible character of keys. We need to mark the last node of every key as end of word node. A Trie node field isEndOfWord is used to distinguish the node as end of word node. A simple structure to represent nodes of the English alphabet can be as following,
// Trie node
struct TrieNode
{
struct TrieNode *children[ALPHABET_SIZE];
// isEndOfWord is true if the node
// represents end of a word
bool isEndOfWord;
};
Inserting a key into Trie is a simple approach. Every character of the input key is inserted as an individual Trie node. Note that the children is an array of pointers (or references) to next level trie nodes. The key character acts as an index into the array children. If the input key is new or an extension of the existing key, we need to construct non-existing nodes of the key, and mark end of the word for the last node. If the input key is a prefix of the existing key in Trie, we simply mark the last node of the key as the end of a word. The key length determines Trie depth.
Searching for a key is similar to insert operation, however, we only compare the characters and move down. The search can terminate due to the end of a string or lack of key in the trie. In the former case, if the isEndofWord field of the last node is true, then the key exists in the trie. In the second case, the search terminates without examining all the characters of the key, since the key is not present in the trie.
The following picture explains construction of trie using keys given in the example below,
root
/ \ \
t a b
| | |
h n y
| | \ |
e s y e
/ | |
i r w
| | |
r e e
|
r
In the picture, every character is of type trie_node_t. For example, the root is of type trie_node_t, and it’s children a, b and t are filled, all other nodes of root will be NULL. Similarly, “a” at the next level is having only one child (“n”), all other children are NULL. The leaf nodes are in blue.
Insert and search costs O(key_length), however the memory requirements of Trie is O(ALPHABET_SIZE * key_length * N) where N is number of keys in Trie. There are efficient representation of trie nodes (e.g. compressed trie, ternary search tree, etc.) to minimize memory requirements of trie.
// C++ implementation of search and insert // operations on Trie #include <bits/stdc++.h> using namespace std;
const int ALPHABET_SIZE = 26;
// trie node struct TrieNode { struct TrieNode *children[ALPHABET_SIZE];
// isEndOfWord is true if the node represents // end of a word bool isEndOfWord; };
// Returns new trie node (initialized to NULLs) struct TrieNode *getNode(void) { struct TrieNode *pNode = new TrieNode;
pNode->isEndOfWord = false;
for (int i = 0; i < ALPHABET_SIZE; i++) pNode->children[i] = NULL;
return pNode; }
// If not present, inserts key into trie // If the key is prefix of trie node, just // marks leaf node void insert(struct TrieNode *root, string key) { struct TrieNode *pCrawl = root;
for (int i = 0; i < key.length(); i++) { int index = key[i] - 'a'; if (!pCrawl->children[index]) pCrawl->children[index] = getNode();
pCrawl = pCrawl->children[index]; }
// mark last node as leaf pCrawl->isEndOfWord = true; }
// Returns true if key presents in trie, else // false bool search(struct TrieNode *root, string key) { struct TrieNode *pCrawl = root;
for (int i = 0; i < key.length(); i++) { int index = key[i] - 'a'; if (!pCrawl->children[index]) return false;
pCrawl = pCrawl->children[index]; }
return (pCrawl != NULL && pCrawl->isEndOfWord); }
// Driver int main() { // Input keys (use only 'a' through 'z' // and lower case) string keys[] = {"the", "a", "there", "answer", "any", "by", "bye", "their" }; int n = sizeof(keys)/sizeof(keys[0]);
struct TrieNode *root = getNode();
// Construct trie for (int i = 0; i < n; i++) insert(root, keys[i]);
// Search for different keys search(root, "the")? cout << "Yes\n" : cout << "No\n"; search(root, "these")? cout << "Yes\n" : cout << "No\n"; return 0; } |
Output:
the --- Present in trie
these --- Not present in trie
their --- Present in trie
thaw --- Not present in trie
Key takeaway
Trie is an efficient information reTrieval data structure. Using Trie, search complexities can be brought to optimal limit (key length). If we store keys in binary search tree, a well-balanced BST will need time proportional to M * log N, where M is maximum string length and N is number of keys in tree. Using Trie, we can search the key in O(M) time. However the penalty is on Trie storage requirements
References:
1. Horowitz, Sahani, Dinesh Mehata, ―Fundamentals of Data Structures in C++‖, Galgotia Publisher, ISBN: 8175152788, 9788175152786.
2. M Folk, B Zoellick, G. Riccardi, ―File Structures‖, Pearson Education, ISBN:81-7758-37-5
3. Peter Brass, ―Advanced Data Structures‖, Cambridge University Press, ISBN: 978-1-107- 43982-5
4. A. Aho, J. Hopcroft, J. Ulman, ―Data Structures and Algorithms‖, Pearson Education, 1998, ISBN-0-201-43578-0.
5. Michael J Folk, ―File Structures an Object-Oriented Approach with C++‖, Pearson Education, ISBN: 81-7758-373-5.
6. Sartaj Sahani, ―Data Structures, Algorithms and Applications in C++‖, Second Edition, University Press, ISBN:81-7371522 X.
7. G A V Pai, ―Data Structures and Algorithms‖, The McGraw-Hill Companies, ISBN - 9780070667266.
8. Goodrich, Tamassia, Goldwasser, ―Data Structures and Algorithms in Java‖, Wiley Publication, ISBN: 9788126551903