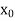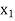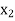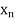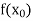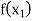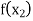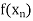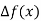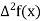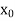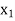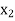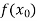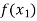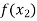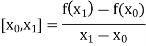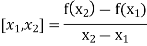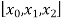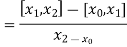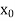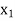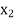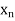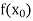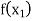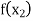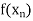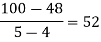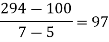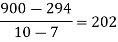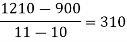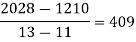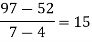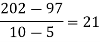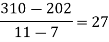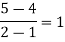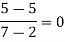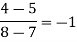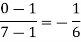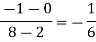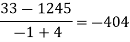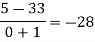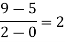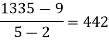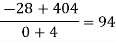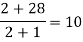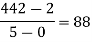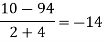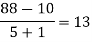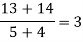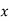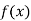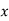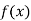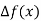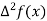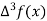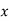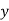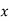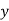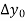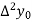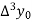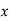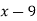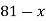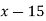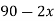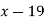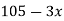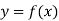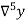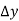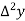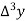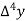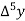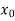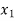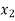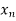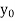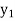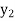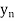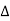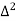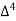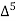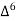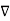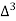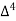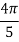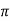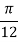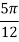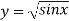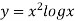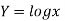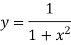Unit-6
Interpolation, Numerical integration, Solution of ordinary differential equations
Interpolation with an unequal interval-
Divided Difference:
In the case of interpolation, when the value of the arguments are not equispaced (unequal intervals) we use the class of differences called divided differences.
Definition: The difference which is defined by taking into consideration the change in the value of the argument are known as divided differences.
Let 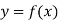 be a function defined as
be a function defined as
|
|
| ……. |
|
|
|
|
………… |
|
Where 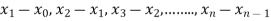 are unequal i.e. it is a case of unequal interval.
are unequal i.e. it is a case of unequal interval.
The First-order divided differences are:
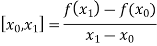
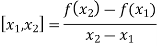
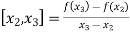 And so on.
And so on.
The second-order divided difference is:
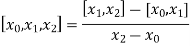
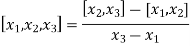
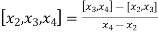 And so on.
And so on.
Similarly, the nth order divided difference is:
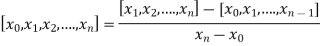
With the help of these we construct the divided difference table:
X | f(x) |
|
|
|
|
|
|
Newton’s Divided difference Formula:
Let 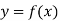 be a function defined as
be a function defined as
|
|
| ……. |
|
|
|
|
………… |
|
Where 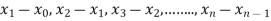 are unequal i.e. it is a case of unequal interval.
are unequal i.e. it is a case of unequal interval.
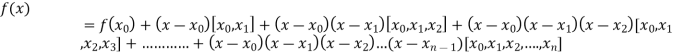 .
.
Example1: Using Newton’s divided difference formula, find the values of 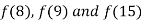 from the following table:
from the following table:
x | 4 | 5 | 7 | 10 | 11 | 13 |
f(x) | 48 | 100 | 294 | 900 | 1210 | 2028 |
We construct the divided difference table is given by:
x | f(x) | First-order divide difference | Second-order divide difference | Third-order divide difference | Fourth-order divide difference |
4
5
7
10
11
13 | 48
100
294
900
1210
2028 |
|
|
|
0
0 |
By Newton’s Divided difference formula
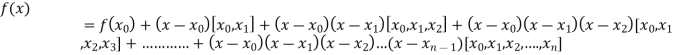 .
.
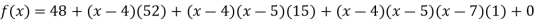
Now, putting 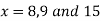 in above we get
in above we get
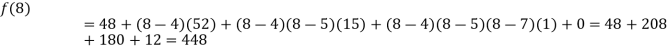 .
.
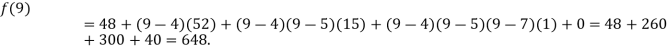
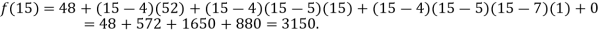
Example2: The following values of the function f(x) for values of x are given:
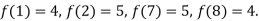
Find the value of 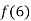 and also the value of x for which f(x) is maximum or minimum.
and also the value of x for which f(x) is maximum or minimum.
We construct the divide difference table:
x | f(x) | First-order divide difference | Second-order divide difference | Third-order divide difference |
1
2
7
8 | 4
5
5
4 |
|
|
0 |
By Newton’s divided difference formula
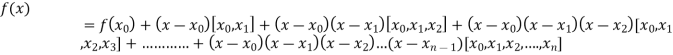 .
.
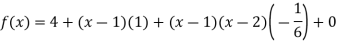
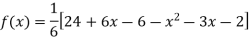
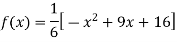
Putting 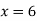 in above we get
in above we get
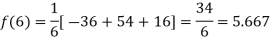
For maximum and minimum of 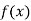 , we have
, we have
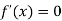
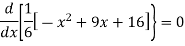
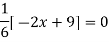
Or 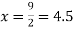
Example3: Find a polynomial satisfied by 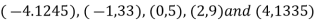 , by the use of Newton’s interpolation formula with a divided difference.
, by the use of Newton’s interpolation formula with a divided difference.
x | -4 | -1 | 0 | 2 | 4 |
F(x) | 1245 | 33 | 5 | 9 | 1335 |
Here
We will construct the divided difference table:
x | F(x) | First-order divided difference | Second-order divided difference | Third-order divided difference | Fourth-order divided difference |
-4
-1
0
2
4 | 1245
33
5
9
1335 |
|
|
|
|
By Newton’s divided difference formula
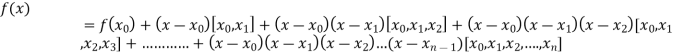 .
.
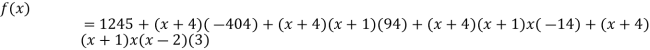
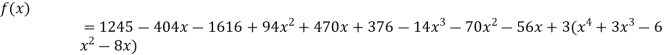
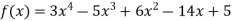
This is the required polynomial.
Newton Forward Difference formula:
This method is useful for interpolation near the beginning of a set of tabular values.
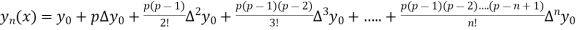
Where 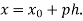
Example1: Using Newton’s forward difference formula, find the sum
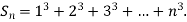
Putting 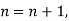
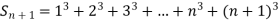
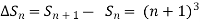
It follows that
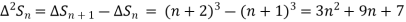
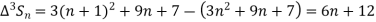
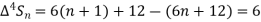
Since 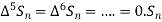 is a fourth-degree polynomial in n.
is a fourth-degree polynomial in n.
Further,
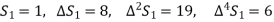
By Newton Forward Difference Method
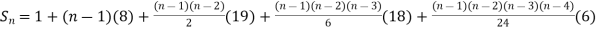
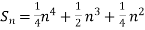
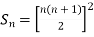
Example2: Given 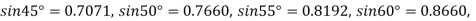 find
find 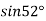 , by using Newton forward interpolation method.
, by using Newton forward interpolation method.
Let 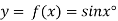 , then
, then
|
|
|
|
|
|
| 0.7071 | 0.7660 | - | 0.8192 | 0.8660 |
The table of forward finite difference is given below:
|
|
|
|
|
45
50
55
60 | 0.7071
0.7660
0.8192
0.8660 |
0.0589
0.0532
0.0468 |
-0.0057
-0.0064 |
-0.0007 |
By Newton forward difference method
Here initial value 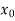 = 45, difference of interval h = 5 and the value to be calculated at x=52.
= 45, difference of interval h = 5 and the value to be calculated at x=52.
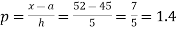
By Formula
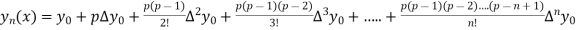
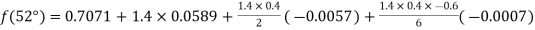
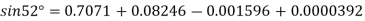
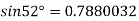
Example3: Find the missing term in the following:
| 0 | 1 | 2 | 3 | 4 |
| 1 | 3 | 9 | ? | 81 |
Let 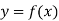
First, we construct the forward difference table:
|
|
|
|
|
0
1
2
3
4 | 1
3
9
81 |
2
6
|
4
|
|
Now, 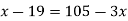
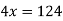
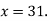
Newton Backward Difference Method:
This method is useful for interpolation near the ending of a set of tabular values.
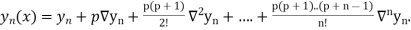
Where 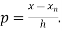
Example1: Find 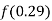 from the following table:
from the following table:
| 0.20 | 0.22 | 0.24 | 0.26 | 0.28 | 0.30 |
| 1.6596 | 1.6698 | 1.6804 | 1.6912 | 1.7024 | 1.7139 |
Consider the backward difference method
|
|
|
|
|
|
|
0.20
0.22
0.24
0.26
0.28
0.30 | 1.6596
1.6698
1.6804
1.6912
1.7024
1.7139 |
0.0102
0.0106
0.0108
0.0112
0.0115 |
0.0004
0.0002
0.0004
0.0003 |
-0.0002
0.0002
-0.0001 |
0.0004
-0.0003 |
-0.0007 |
Here 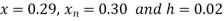
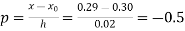
By Newton backward difference formula
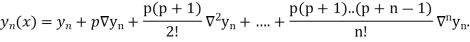
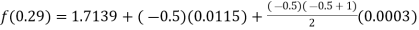
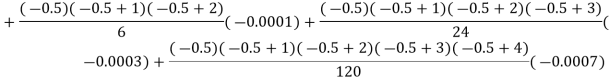
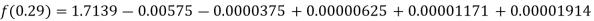
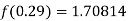
Example2:The following table gives the amount of a chemical dissolved in water:
Temp. |
|
|
|
|
|
|
Solubility | 19.97 | 21.51 | 22.47 | 23.52 | 24.65 | 25.89 |
Compute the amount dissolve at 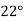
Consider the following backward difference table:
Temp. x | Solubility y |
|
|
|
|
|
10
15
20
25
30
35 | 19.97
21.51
22.47
23.52
24.65
25.89 |
1.54
0.96
1.05
1.13
1.24 |
-0.58
0.09
0.08
0.11 |
0.67
-0.01
0.03 |
-0.68
0.04 |
0.72 |
Here 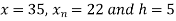
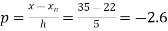
By Newton Backward difference formula
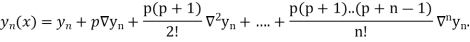
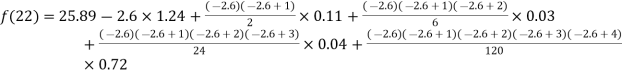
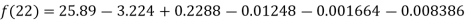
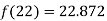
Example3: The following are the marks obtained by492 candidate in a certain examination
Marks | 0-40 | 40-45 | 45-50 | 50-55 | 55-60 | 60-65 |
No. of candidates | 210 | 43 | 54 | 74 | 32 | 79 |
Find out the number of candidates:
a) Who secured more than 48 but not more than 50 marks?
b) Who secured less than 48 but not less than 45 marks?
Consider the forward difference table given below:
Marks up to x | No. of candidates y |
|
|
|
|
|
40
45
50
55
60
65 | 210
210+43=253
253+54=307
307+74=381
381+32=413
413+79= 492 |
43
54
74
32
79 |
11
20
-42
47 |
9
-62
89 |
-71
151 |
222 |
Here 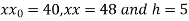
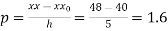
By Newton Forward Difference formula
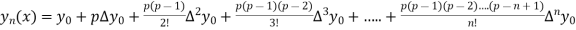
f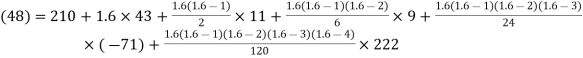
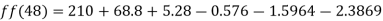
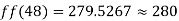
a) No. of candidate secured more than 48 but not more than 50 marks
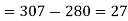
b) No. of candidate secured less than 48 but not less than 45 marks
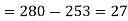
Lagrange interpolation
Given a set of values of x and y, the process of finding the value of x for a certain value of y is called inverse interpolation.
Lagrange’s Inverse interpolation:
Let 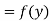 , be defined function we get
, be defined function we get
x |
|
|
| ….. |
|
f(Y) |
|
|
| …… |
|
Where the interval is not necessarily equal. We assume f(x) is a polynomial of degree n. Then Lagrange’s inverse interpolation formula is given by
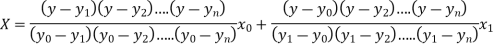
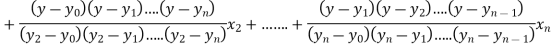
Example1: Use the inverse interpolation to find the value of x at 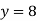 for the following data:
for the following data:
X | 1 | 3 | 4 |
Y | 4 | 12 | 19 |
Here 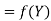 , we have the data
, we have the data
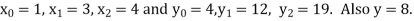
Lagrange’s inverse interpolation formula is given by
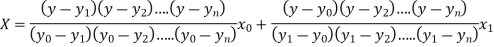
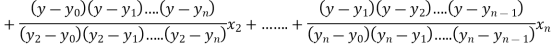
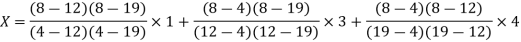
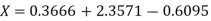
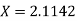 .
.
Example2: Use the inverse Lagrange’s method to find the root of the equation 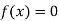 , give data
, give data 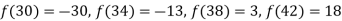
X | 30 | 34 | 38 | 42 |
F(x) | -30 | -13 | 3 | 18 |
Here 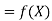 , we have the data
, we have the data
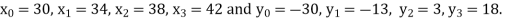
Also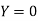 .
.
Lagrange’s inverse interpolation formula is given by
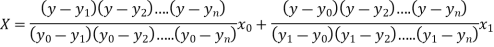
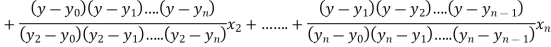
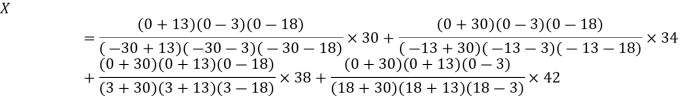
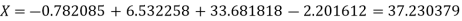
Thus the approximate root of the given equation is 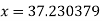 .
.
Example3: Find the value of x at 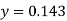 for the following data:
for the following data:
X | 1 | 2 | 4 | 5 | 8 |
Y | 1.000 | 0.500 | 0.250 | 0.200 | 0.125 |
Here 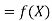 , we have the data
, we have the data
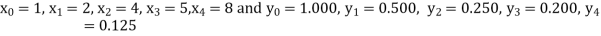
Also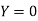 .
.
Lagrange’s inverse interpolation formula is given by
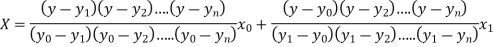
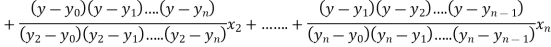

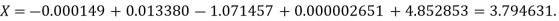
Thus the value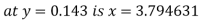 .
.
Newton’s forward Difference formula:
This method is useful for interpolation near the beginning of a set of tabular values.
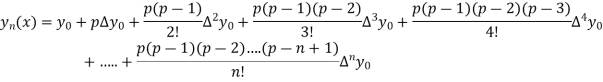
Where 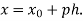
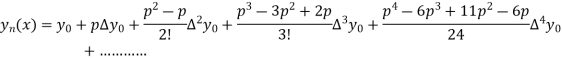
Differentiating both sides with respect to p, we get
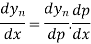
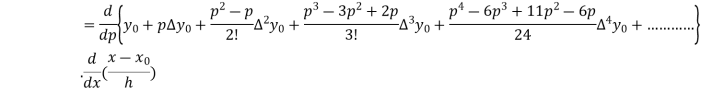
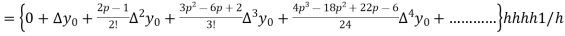 h
h
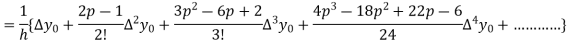
This formula is applicable to compute the value of 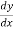 for non-tabular values of x.
for non-tabular values of x.
For tabular values of x, we can get formula by putting 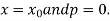
Therefore
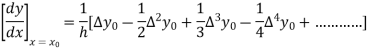
Similarly, we can get the formula for higher-order by differentiating the previous order formulas
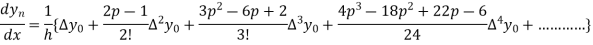
Again differentiating with respect to p, we get
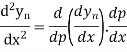
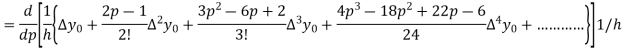
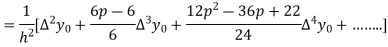
Hence
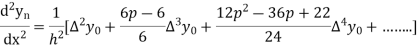
Also
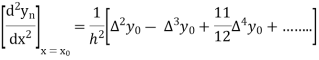
And so on.
Example1:Given that
X | 1.0 | 1.1 | 1.2 | 1.3 |
Y | 0.841 | 0.891 | 0.932 | 0.963 |
Find 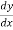 at
at 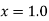 .
.
Here the first derivative is to be calculated at the beginning of the table, therefore forward difference formula will be used
Forward difference table is given below:
X | Y |
|
|
|
1.0
1.1
1.2
1.3 | 0.841
0.891
0.932
0.962 |
0.050
0.041
0.031 |
-0.009
-0.010 |
-0.001 |
By Newton’s forward differentiation formula for differentiation
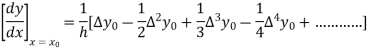
Here 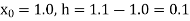
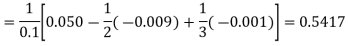
Example2: Find the first and second derivatives of the function given below at the point 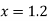 :
:
X | 1 | 2 | 3 | 4 | 5 |
Y | 0 | 1 | 5 | 6 | 8 |
Here the point of the calculation  is at the beginning of the table,
is at the beginning of the table,
Forward difference table is given by:
X | Y |
|
|
|
|
1
2
3
4
5 | 0
1
5
6
8 |
1
4
1
2 |
3
-3
1 |
-6
4
|
-10
|
By Newton’s forward differentiation formula for differentiation
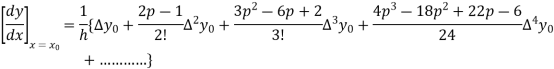
Here 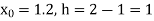 ,
, 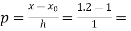 0.
0.
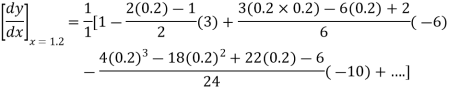
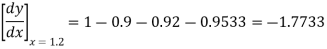
Again
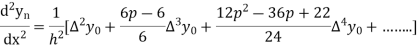
At 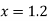
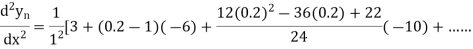
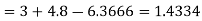
Example3: From the following table of values of x and y find 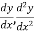 for
for 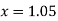
X | 1.00 | 1.05 | 1.10 | 1.15 | 1.20 | 1.25 | 1.30 |
Y | 1.0000 | 1.02470 | 1.04881 | 1.07238 | 1.09544 | 1.11803 | 1.14017 |
Here the value of the derivative is to be calculated at the beginning of the table.
Forward difference table is given by
X | Y |
|
|
|
|
|
|
1.00
1.05
1.10
1.15
1.20
1.25
1.30 | 1.0000
1.02470
1.04881
1.07238
1.09544
1.11803
1.14017 |
0.02470
0.02411
0.02357
0.02306
0.02259
0.02214 |
-0.00059
-0.00054
-0.00051
-0.00047
-0.00045 |
0.00005
0.00003
0.00004
0.00002 |
-0.00002
0.00001
-0.00002 |
0.00003
-0.00003 |
-0.00006 |
From Newton’s forward difference formula for differentiation we get
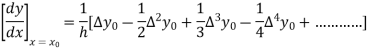
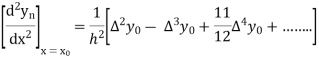
Here 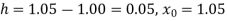
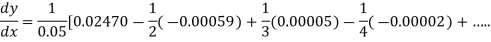
=0.48763
Newton Backward Difference Method:
This method is useful for interpolation near the ending of a set of tabular values.
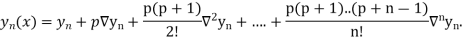
Where 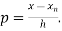
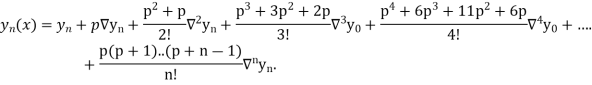
Differentiating both sides with respect to p, we get
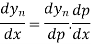
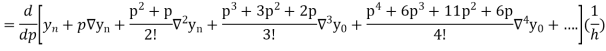
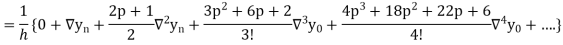
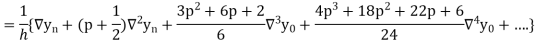
This formula is applicable to compute the value of 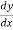 for non-tabular values of x.
for non-tabular values of x.
For tabular values of x, we can get formula by putting 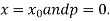
Therefore
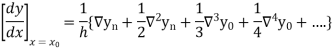
Similarly, we can get the formula for higher-order by differentiating the previous order formulas
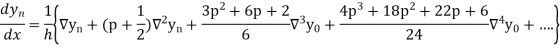
Differentiating both sides with respect to p, we get
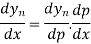
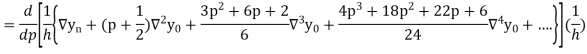
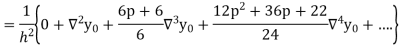
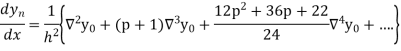
Also
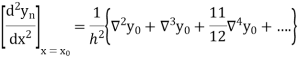
Example1:Given that
X | 0.1 | 0.2 | 0.3 | 0..4 |
Y | 1.10517 | 1.22140 | 1.34986 | 1.49182 |
Find 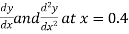 ?
?
Backward difference table:
X | Y |
|
|
|
0.1
0.2
0.3
0.4 | 1.10517
1.22140
1.34986
1.49182 |
0.11623
0.12846
0.14196 |
0.01223
0.01350 |
0.00127 |
Newton’s Backward formula for differentiation
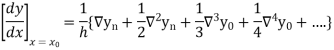
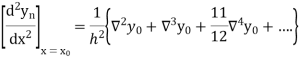
Here 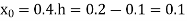
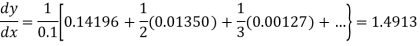
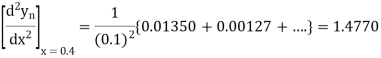
Example2: Given that
X | 1.0 | 1.2 | 1.4 | 1.6 | 1.8 | 2.0 |
Y | 0 | 0.128 | 0.544 | 1.296 | 2.432 | 4.0 |
Find the derivative of y at 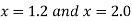 ?
?
The difference table is given below:
X | Y |
|
|
|
|
1.0
1.2
1.4
1.6
1.8
2.0 | 0
0.128
0.544
1.296
2.432
4.0 |
0.128
0.416
0.752
0.136
1.568
|
0.288
0.336
0.384
0.432 |
0.048
0.048
0.048 |
0
0 |
Since the point 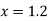 is at the beginning of the table therefore
is at the beginning of the table therefore
From Newton’s forward difference formula for differentiation we get
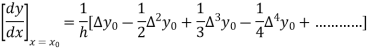
Here 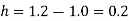
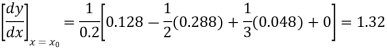
Since the point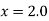 is at the end of the table therefore
is at the end of the table therefore
Backward difference table is :
X | Y |
|
|
|
|
1.0
1.2
1.4
1.6
1.8
2.0 | 0
0.128
0.544
1.296
2.432
4.000 |
0.128
0.416
0.752
0.136
1.568 |
0.288
0.336
0.384
0.432 |
0.048
0.048
0.048 |
0
0 |
Newton’s Backward formula for differentiation
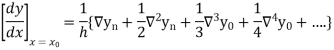
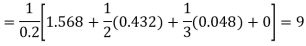
Numerical integration is a process of evaluating or obtaining a definite integral 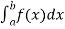 from a set of numerical values of the integrand f(x).In the case of the function of a single variable, the process is called quadrature.
from a set of numerical values of the integrand f(x).In the case of the function of a single variable, the process is called quadrature.
Trapezoidal Method:
Let the interval 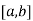 be divided into n equal intervals such that
be divided into n equal intervals such that 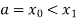 <
<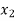 <….<
<….<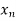 =b.
=b.
Here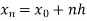 .
.
To find the value of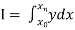 .
.
Setting n=1, we get
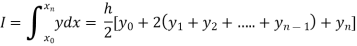
Or I = 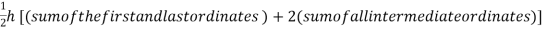
The above is known as the Trapezoidal method.
Note: In this method second and higher differences are neglected and so f(x) is a polynomial of degree 1.
Geometrical Significance: The curve y=f(x), is replaced by n straight lines with the points 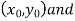 (
(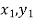 );(
);(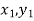 ) and (
) and (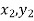 );…….;(
);…….;(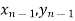 ) and (
) and (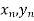 ).
).
The area bounded by the curve y=f(x), the ordinates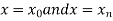 , and the x-axis is approximately equivalent to the sum of the area of the n trapeziums obtained.
, and the x-axis is approximately equivalent to the sum of the area of the n trapeziums obtained.
Example1: State the trapezoidal rule for finding an approximate area under the given curve. A curve is given by the points (x, y) given below:
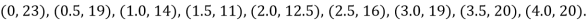
Estimate the area bounded by the curve, the x-axis, and the extreme ordinates.
We construct the data table:
X | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Y | 23 | 19 | 14 | 11 | 12.5 | 16 | 19 | 20 | 20 |
Here length of interval h =0.5, initial value a = 0 and final value b = 4
By Trapezoidal method
Area of curve bounded on x-axis =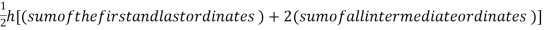
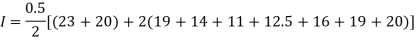
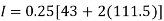
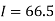
Example2: Compute the value of 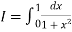 ?
?
Using the trapezoidal rule with h=0.5, 0.25, and 0.125.
Here 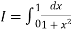
For h=0.5, we construct the data table:
X | 0 | 0.5 | 1 |
Y | 1 | 0.8 | 0.5 |
By Trapezoidal rule
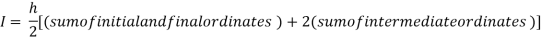
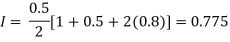
For h=0.25, we construct the data table:
X | 0 | 0.25 | 0.5 | 0.75 | 1 |
Y | 1 | 0.94117 | 0.8 | 0.64 | 0.5 |
By Trapezoidal rule
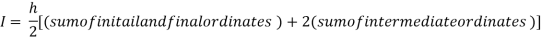
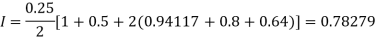
For h = 0.125, we construct the data table:
X | 0 | 0.125 | 0.25 | 0.375 | 0.5 | 0.625 | 0.75 | 0.875 | 1 |
Y | 1 | 0.98461 | 0.94117 | 0.87671 | 0.8 | 0.71910 | 0.64 | 0.56637 | 0.5 |
By Trapezoidal rule
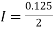 [(1+0.5)+2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]
[(1+0.5)+2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]
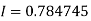
Example3:Evaluate , using trapezoidal rule with five ordinates
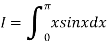
Here 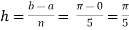
We construct the data table:
X | 0 |
|
|
|
|
|
Y | 0 | 0.3693161 | 1.195328 | 1.7926992 | 1.477265 | 0 |
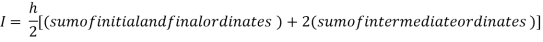
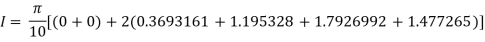
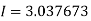
Simpson’s Rule:
Let the interval 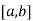 be divided into n equal intervals such that
be divided into n equal intervals such that 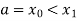 <
<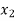 <….<
<….<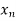 =b.
=b.
Here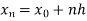 .
.
To find the value of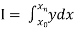 .
.
Setting n = 2,
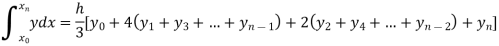
Which is known as Simpson’s 1/3- rule or Simpson’s rule.
Note: In this rule third and higher differences are neglected a so f(x) is a polynomial of degree 2.
Example1: Estimate the value of the integral
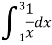
by Simpson’s rule with 4 strips and 8 strips respectively.
For n=4, we have 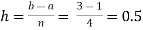
Construct the data table:
X | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
Y=1/x | 1 | 0.66666 | 0.5 | 0.4 | 0.33333 |
By Simpson’s Rule
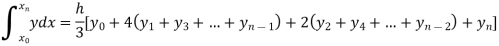
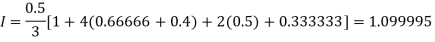
For n = 8, we have 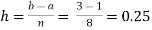
X | 1 | 1.25 | 1.50 | 1.75 | 2.0 | 2.25 | 2.50 | 2.75 | 3.0 |
Y=1/x | 1 | 0.8 | 0.66666 | 0.571428 | 0.5 | 0.444444 | 0.4 | 0.3636363 | 0.333333 |
By Simpson’s Rule
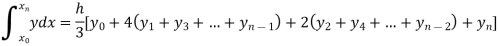
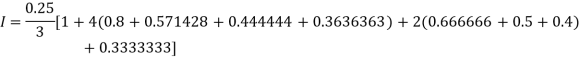
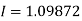
Example2: Evaluate 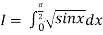
Using Simpson’s 1/3 rule with 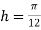 .
.
For 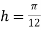 , we construct the data table:
, we construct the data table:
X | 0 |
|
|
|
|
|
|
| 0 | 0.50874 | 0.707106 | 0.840896 | 0.930604 | 0.98281 | 1 |
By Simpson’s Rule
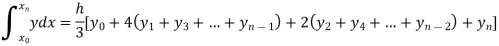
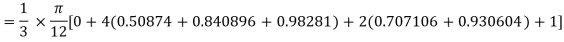
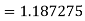
Example3: Using Simpson’s 1/3 rule with h = 1, evaluate
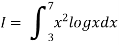
For h = 1, we construct the data table:
X | 3 | 4 | 5 | 6 | 7 |
| 9.88751 | 22.108709 | 40.23594 | 64.503340 | 95.34959 |
By Simpson’s Rule
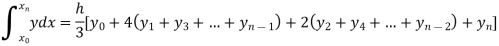
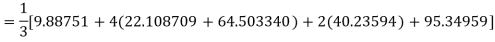
= 177.3853
Simpson’s 3/8 rule
Let the interval 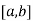 be divided into n equal intervals such that
be divided into n equal intervals such that 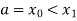 <
<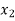 <….<
<….<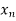 =b.
=b.
Here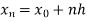 .
.
To find the value of 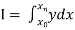 .
.
Setting n=3, we get
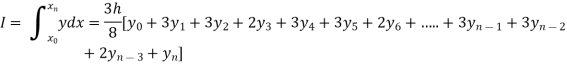
Is known as Simpson’s 3/8 rule which is not as accurate as Simpson’s rule.
Note: In this rule, the fourth and higher differences are neglected and so f(x) is a polynomial of degree 3.
Example1: Evaluate 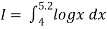
By Simpson’s 3/8 rule.
Let us divide the range of the interval [4, 5.2] into six equal parts.
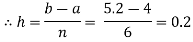
For h=0.2, we construct the data table:
X | 4.0 | 4.2 | 4.4 | 4.6 | 4.8 | 5.0 | 5.2 |
| 1.3863 | 1.4351 | 1.4816 | 1.5261 | 1.5686 | 1.6094 | 1.6487 |
By Simpson’s 3/8 rule
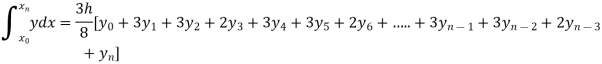

= 1.8278475
Example2: Evaluate 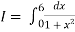
Let us divide the range of the interval [0,6] into six equal parts.
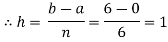
For h=1, we construct the data table:
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 0.5 | 0.2 | 0.1 | 0.0588 | 0.0385 | 0.027 |
By Simpson’s 3/8 rule
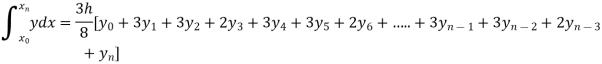
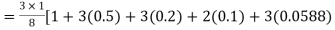 +3(0.0385)+0.027]
+3(0.0385)+0.027]
=1.3571
Error in Simpson’s 3/8 Rule
The error in this rule is given by
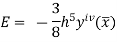
Where 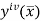 is the largest value of the derivative of y(x).
is the largest value of the derivative of y(x).
Error in Trapezoidal method
The total error in the trapezoidal method is given by
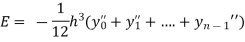
Let 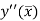 is the largest value of the n quantities on the right-hand side of the above equation then
is the largest value of the n quantities on the right-hand side of the above equation then
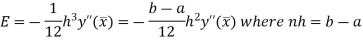
Error in Simpson’s Rule
The error in Simpson’s rule is given by
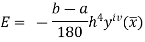
Where 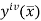 is the largest value of the fourth derivative of y(x).
is the largest value of the fourth derivative of y(x).
Error in Simpson’s 3/8 Rule
The error in this rule is given by
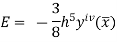
Where 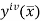 is the largest value of the derivative of y(x).
is the largest value of the derivative of y(x).
Euler’s Method:
The general First-order differential equation
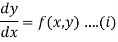
With the initial condition 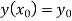
In this method, the solution is in the form of tabulated values.
Integrating both side of the equation (i) we get
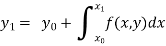
Assuming that 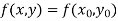 in
in 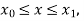 this gives Euler’s formula
this gives Euler’s formula
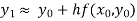
In general formula
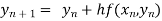 , n=0,1,2,…..
, n=0,1,2,…..
Error estimate for the Euler’s method
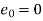
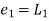
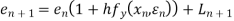
Example1:Use Euler’s method to find y(0.4) from the differential equation
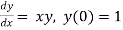 with h=0.1
with h=0.1
Given equation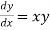
Here 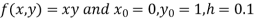
We break the interval into four steps.
So that 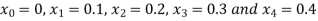
By Euler’s formula
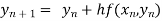 , n=0,1,2,3 ……(i)
, n=0,1,2,3 ……(i)
For n=0 in equation (i) we get
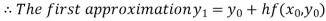
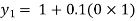
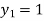
For n=1 in equation (i) we get
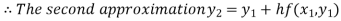
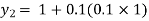
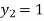 .01
.01
For n=2 in equation (i) we get
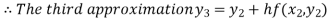
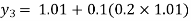
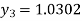
For n=3 in equation (i) we get
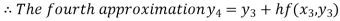
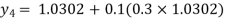
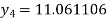
Hence y(0.4) =1.061106.
Example2:Using Euler’s method solves the differential equation for y at x=1 in five steps
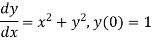
Given equation 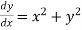
Here 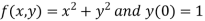
No. of steps n=5 and so that 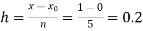
So that 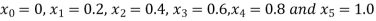
Also 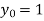
By Euler’s formula
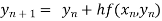 , n=0,1,2,3,4 ……(i)
, n=0,1,2,3,4 ……(i)
For n=0 in equation (i) we get
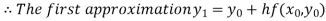
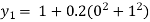
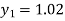
For n=1 in equation (i) we get
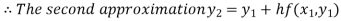
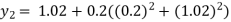
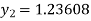
For n=2 in equation (i) we get
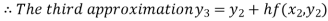
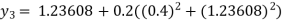
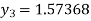
For n=3 in equation (i) we get
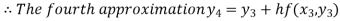
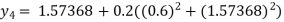
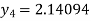
For n=4 in equation (i) we get
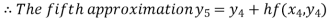
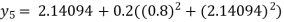
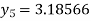
Hence 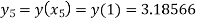
Example3:Given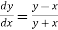 with the initial condition y=1 at x=0.Find y for x=0.1 by Euler’s method(five steps).
with the initial condition y=1 at x=0.Find y for x=0.1 by Euler’s method(five steps).
Given equation is 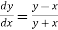
Here 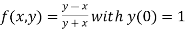
No. of steps n=5 and so that 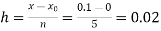
So that 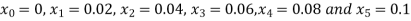
Also 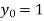
By Euler’s formula
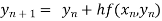 , n=0,1,2,3,4 ……(i)
, n=0,1,2,3,4 ……(i)
For n=0 in equation (i) we get
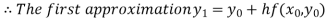
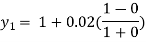
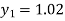
For n=1 in equation (i) we get
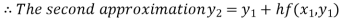
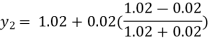
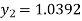
For n=2 in equation (i) we get
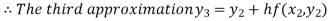
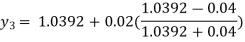
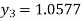
For n=3 in equation (i) we get
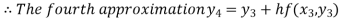
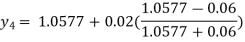
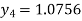
For n=4 in equation (i) we get
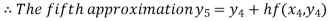
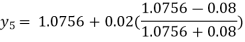
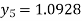
Hence 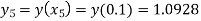
Modified Euler’s Method:
Instead of approximating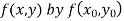 as in Euler’s method. In the modified Euler’s method, we have the iteration formula
as in Euler’s method. In the modified Euler’s method, we have the iteration formula
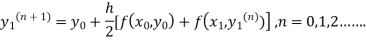
Where 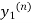 is the nth approximation to
is the nth approximation to 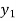 .The iteration started with Euler’s formula
.The iteration started with Euler’s formula
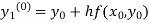
Example1: Use modified Euler’s method to compute y for x=0.05. Given that
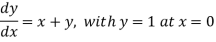
The result correct to three decimal places.
Given equation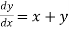
Here 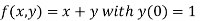
Take h = 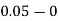 = 0.05
= 0.05
By modified Euler’s formula, the initial iteration is
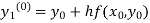
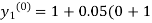 )
)
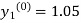
The iteration formula by modified Euler’s method is
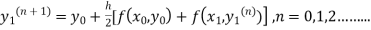 -----(i)
-----(i)
For n=0 in equation (i) we get
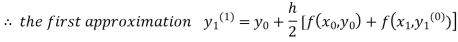
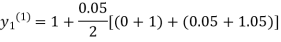
Where 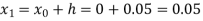 and
and 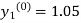 as above
as above
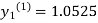
For n=1 in equation (i) we get
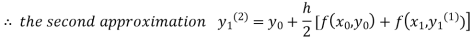
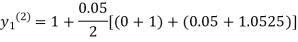
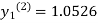
For n=3 in equation (i) we get
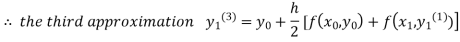
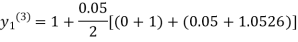
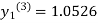
Since the third and fourth approximation is equal.
Hence y=1.0526 at x = 0.05 correct to three decimal places.
Example2: Using modified Euler’s method, obtain a solution of the equation
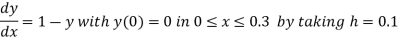
Given equation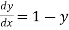
Here 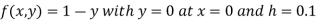
By modified Euler’s formula, the initial iteration is
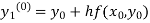
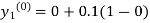
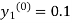
The iteration formula by modified Euler’s method is
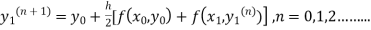 -----(i)
-----(i)
For n=0 in equation (i) we get
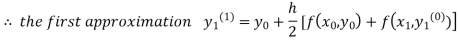
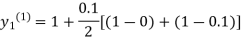
Where 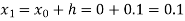 and
and 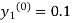 as above
as above
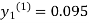
For n=1 in equation (i) we get
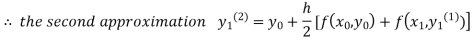
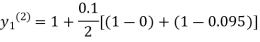
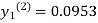
For n=2 in equation (i) we get
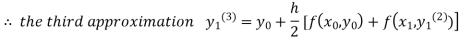
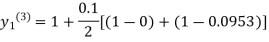
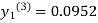
For n=3 in equation (i) we get
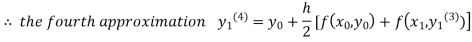
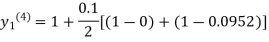
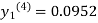
Since the third and fourth approximation is equal.
Hence y=0.0952 at x=0.1
To calculate the value of 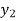 at x=0.2
at x=0.2
By modified Euler’s formula, the initial iteration is
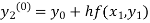
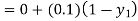
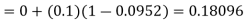
The iteration formula by modified Euler’s method is
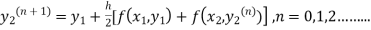 -----(ii)
-----(ii)
For n=0 in equation (ii) we get
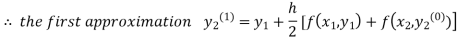
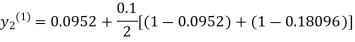
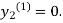 1814
1814
For n=1 in equation (ii) we get
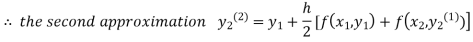
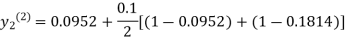
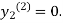 1814
1814
Since the first and second approximations are equal.
Hence y = 0.1814 at x=0.2
To calculate the value of 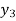 at x=0.3
at x=0.3
By modified Euler’s formula, the initial iteration is
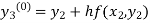
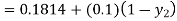
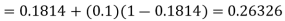
The iteration formula by modified Euler’s method is
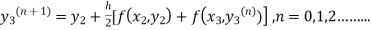 -----(iii)
-----(iii)
For n=0 in equation (iii) we get
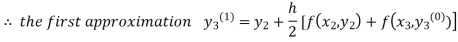
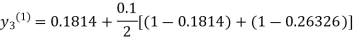
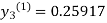
For n=1 in equation (iii) we get
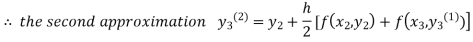
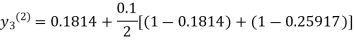
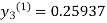
For n=2 in equation (iii) we get
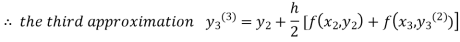
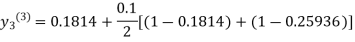
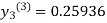
For n=3 in equation (iii) we get
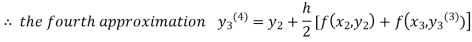
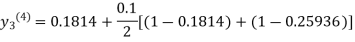
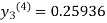
Since the third and fourth approximations are the same.
Hence y = 0.25936 at x = 0.3
This method is more accurate than Euler’s method.
Consider the differential equation of First-order
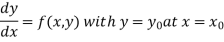
Let 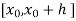 be the first interval.
be the first interval.
A Second-order Runge-Kutta formula
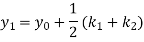
Where 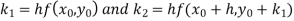
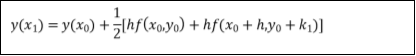 Rewrite as
Rewrite as
A fourth orderRunge-Kutta formula:
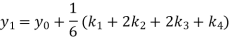
Where 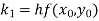
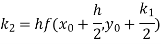
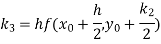
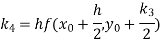
Example1: Use Runge-Kutta method to find y when x=1.2 in the step of h=0.1 given that
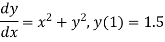
Given equation 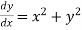
Here 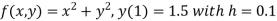
Also 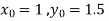
By Runge-Kutta formula for first interval
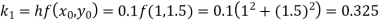
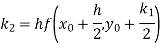
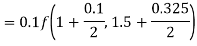
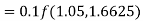
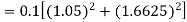
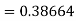
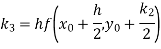
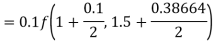
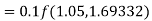
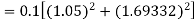
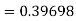
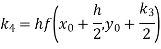
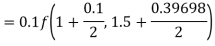
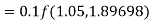
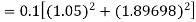
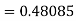
Again 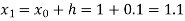
A fourth orderRunge-Kutta formula:
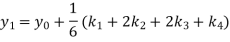

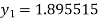
To find y at 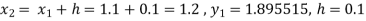
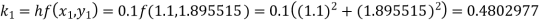
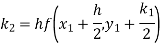
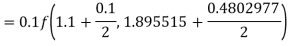
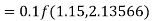
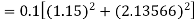
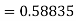
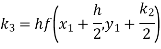
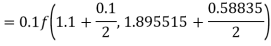
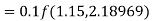
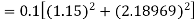
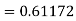
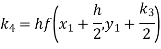
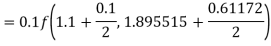
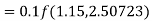
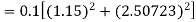
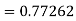
A fourth orderRunge-Kutta formula:
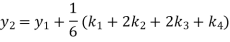

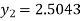
Example2: Apply Runge-Kutta fourth-order method to find an approximate value of y for x=0.2 in the step of 0.1, if
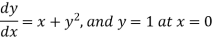
Given equation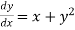
Here 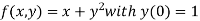
Also 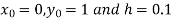
By Runge-Kutta formula for first interval
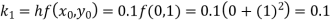
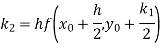
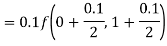
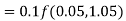
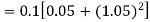
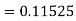
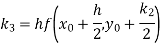
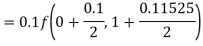
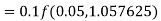
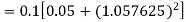
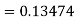
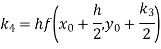
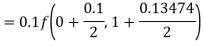
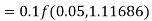
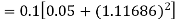
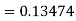
A fourth orderRunge-Kutta formula:
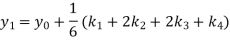
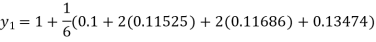
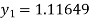
Again 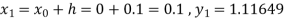
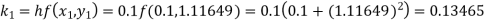
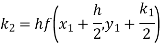
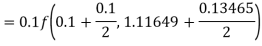
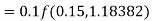
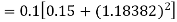
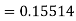
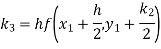
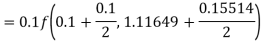
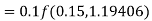
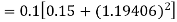
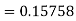
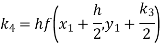
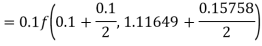
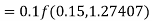
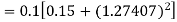
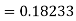
A fourth orderRunge-Kutta formula:
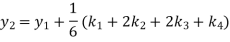
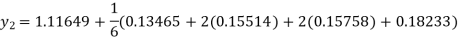
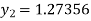
Example3: Using the Runge-Kutta method of fourth-order, solve
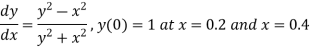
Given equation 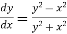
Here 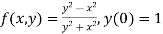
Also 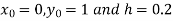
By Runge-Kutta formula for first interval
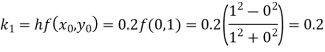
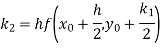
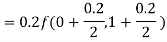
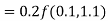
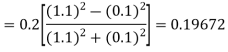
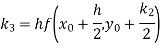
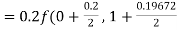 )
)
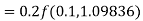
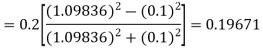
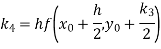
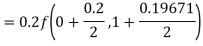
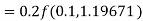
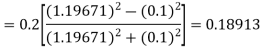
A fourth orderRunge-Kutta formula:
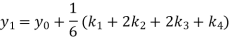
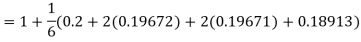
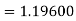
Hence at x = 0.2 then y = 1.196
To find the value of y at x=0.4. In this case 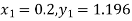
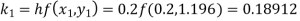
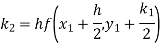
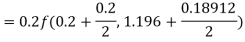
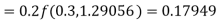
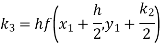
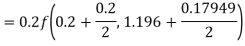
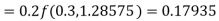
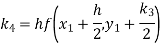
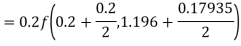
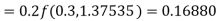
A fourth orderRunge-Kutta formula:
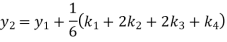
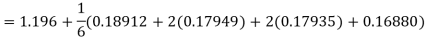
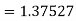
Hence at x = 0.4 then y=1.37527
The solution of Second-order ODE using the 4th order Runge-Kutta method:
The Second-order differential equation
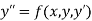
Let 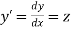 then the above equation reduces to a First-order simultaneous differential equation
then the above equation reduces to a First-order simultaneous differential equation
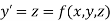
Then 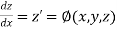
This can be solved as we discuss above by Runge-Kutta Method. Here 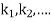 for
for 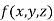 and
and 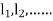 for
for 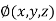 .
.
A fourth orderRungeKutta formula:
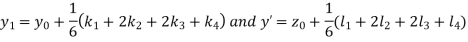
Where 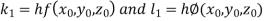
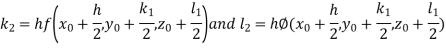
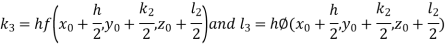
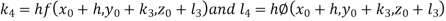
Example1: UsingRungeKutta method of order four, solve 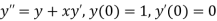 to find
to find 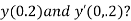
Given Second-order differential equation is
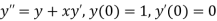
Let 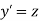 then above equation reduces to
then above equation reduces to
Or 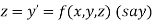
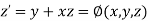 (say)
(say)
Or 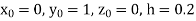 .
.
By RungeKutta Method we have
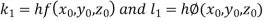
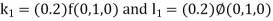
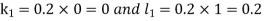
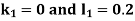
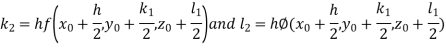
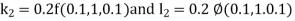
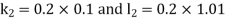
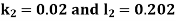
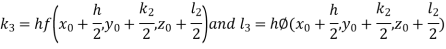
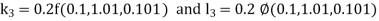
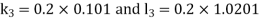
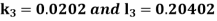
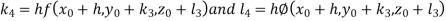
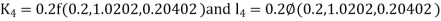
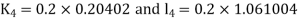
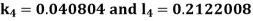
A fourth orderRungeKutta formula:
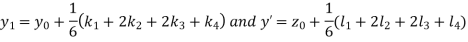

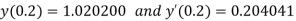
Example2: Using the RungeKutta method, solve
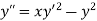 for
for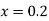 correct to four decimal places with initial condition
correct to four decimal places with initial condition 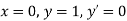 .
.
Given Second-order differential equation is
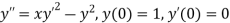
Let 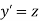 then above equation reduces to
then above equation reduces to
Or 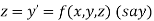
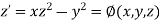 (say)
(say)
Or 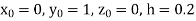 .
.
By RungeKutta Method we have
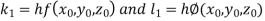
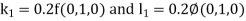
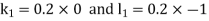
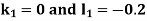
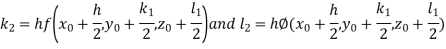
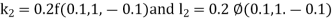
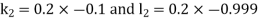
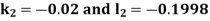
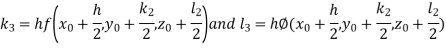
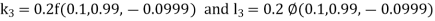
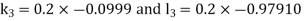
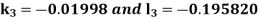
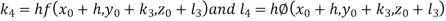
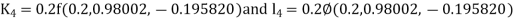
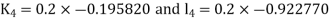

A fourth orderRungeKutta formula:
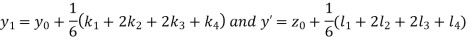
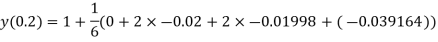
And 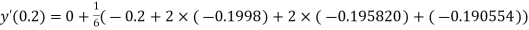
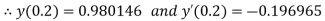 .
.
Example3: Solve the differential equations
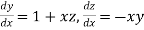 for
for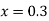
Using the four order RungeKutta method with initial conditions 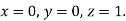
Given differential equation are
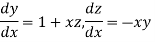
Let 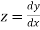
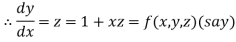
And 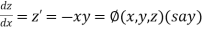
Also 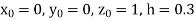
By RungeKutta Method we have
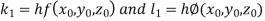
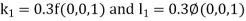
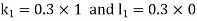
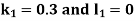
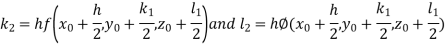
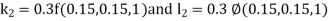
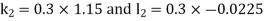
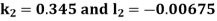
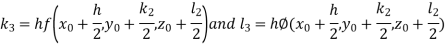
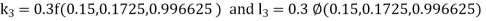
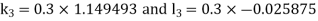
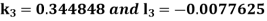
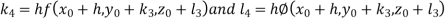
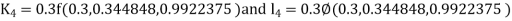
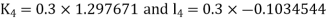

A fourth orderRungeKutta formula:
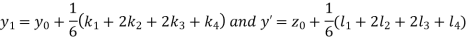
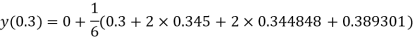
And 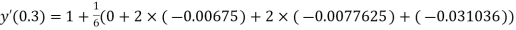
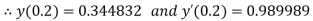 .
.
Predictor and corrector-
Predicator and corrector method uses more than one previous step to calculate the next value of y.
A general form predictor and corrector method is-
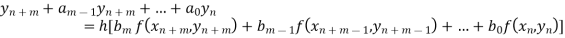
Where 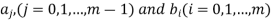 are the constants to be determined.
are the constants to be determined.
Note-
References
1. Erwin Kreyszig, Advanced Engineering Mathematics, 9thEdition, John Wiley & Sons, 2006.
2. N.P. Bali and Manish Goyal, A textbook of Engineering Mathematics, Laxmi Publications.
3. Higher engineering mathematic, Dr. B.S. Grewal, Khanna publishers