UNIT - 2
Z-transform and Pulse-transfer-function
The most important use of z-transform is its ability to completely characterise signals and linear systems in the most general ways possible. The z-transform is primarily used to convert the discrete time domain signal into discrete frequency domain signal. The z-transform for LTI system is defined as
H(z)=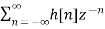
The z-transform of basic signals with ROC is given below
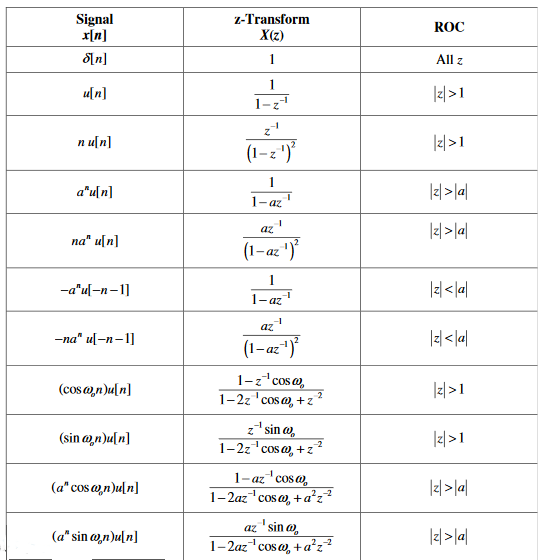
Region of Convergence (ROC):
The range of variation of z for which z-transform converges is called region of convergence of z-transform.
Properties of ROC of Z-Transforms
- ROC does not contain any poles.
- If x(n) is a finite sequence and x(z) converges for some value of z, then ROC can be entire z plane except at z=0 and ∞.
- If x(n) is a right sided sequence and x(z) converges for some value of z, then the ROC is the of the form |z|>Rmax where Rmax is the radius.
- If x(n) is left sided sequence and x(z) converges for some value of z then the ROC is of the form |z|<Rmin where Rmin is the smallest magnitude of any pole of x(z). Thus, the ROC is the entire circle having Rmin.
- If x(n) is a double sided sequence and x(z) converges for some value of z then the ROC is of the form
R1 <|z| < R2
Rmin < |z| <Rmax.
Where R1, R2 are the magnitude of two poles of x(z)
Initial Value and Final Value Theorems
Initial value and final value theorems of z-transform are defined for causal signal.
Initial Value Theorem
For a causal signal x(n), the initial value theorem states that
x(0) = ltz→∞X(z)
This is used to find the initial value of the signal without taking inverse z-transform
Final Value Theorem
For a causal signal x(n), the final value theorem states that
x(∞) = ltz→1[z−1]X(z)
This is used to find the final value of the signal without taking inverse z-transform.
Properties of z-transform:
a) Linearity Property:
x1[n]- X1[z]
x2[n]X2[z]
x[n]=a1x1[n]+a2x2[n]
X[z]=a1X1[z]+a2X2[z]
a1x1[n]+a2x2[n] = a1X1[z]+a2X2[z]
b) Time shifting Property:
X(n-n0)X(z)Z-n
X(n-1) z-1X(z)
c) Time Scaling Property:
anx(n)X(a-1z)
d) Differentiation Property:
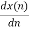=(1-z-1)X(z)
e) Convolution:
x1(n)*x2(n)X1(z).X2(z)
f) Differentiation in frequency:
Nx(n)-z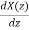
g) Multiplication in time:
x1(n).x2(n)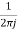
[X1(z)*X2(z)]
h) Conjugation in time:
X*(n)X*(z*)
The inverse z-transform can be determined by two methods
1) Power Series Method
Que) Find the inverse z-transform of X(z)=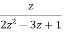
, |z|<
?
Sol: Finding inverse z-transform by power series method
X(z)=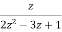
ROC :|z|<
From the given ROC it is clear that the sequence is left sided. Hence, the power of z should be positive.
1-3z+2z2) z (z+3z2+7z3+15z4
- z-3z2+2z3
-----------------
3z2-2z3
- 3z2-9z3+6z4
-----------------
7z3-6z4
- 7z3-21z4+14z5
-------------------
15z4-14z5
- 15z4-45z5+30z6
-------------------
31z5-30z6
=z+3z2+7z3+15z4+31z5+…………
=…………+15z4+7z3+3z2+z
=………….+15z-(-4)+7z-(-3)+3z-(-2)+z
X[n]={…….15,7,3,1,0}
2) Partial Fraction Method
Que) Find the inverse z-transform of X(z)=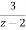
. Using partial fraction method. ROC |z|>2?
Sol: X(z)=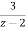
Dividing both sides by z
=
=
+
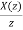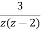
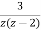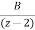
3=A(z-2)+Bz
Equating coefficients of z and z0 on both sides we get
A+B=0
-2A+B=3
Solving above two equations and we get A=-3/2 and B=3/2
=
+
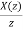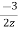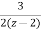
X(z)=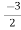
+
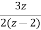
Taking inverse of above equation
X[n]=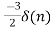
+
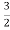(2)nu(n) [refer above table of z-transform]
The z transform is used to find the solution of linear differential equation with constant coefficients. Considering the sequence of form x[n-m], where m=1. Therefore, from definition of z-transform
Z{x[n-1]} =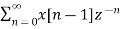 
=x(-1)+x(0)z-1+x(1)z-2+x(2)z-3+……..
=x(-1)+z-1[x(0)+x(1)z-1+x(2)z-2+……..]
Z{x[n-1]}=x(-1)+z-1X(z)
Generalised form can be Z[x(n-m)]=z-mZ[X(z)]
Z [x (n + 1)] = zZ [x (n)] − zx (0) = z [X (z) − x (0)]
Z[x(n+2)] = z2 [X (z) − x (0) -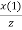 
]
Z[x(n+3)] = z3 [X (z) − x (0) -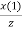 
- 
]
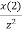Procedure for solution of difference equation
(i) Apply Z-transform on both sides of given difference equation.
(ii) Expand formulae.
(iii) Take Z[x(n)] as one side of the equation and remaining other side.
(iv) Take Z −1 on both sides.
(v) Apply partial fraction or power series method to find IZT.
Que) Solve the second order difference equation 2x(n-2)-2x(n-1)+x(n)=3n-2 n>0, where x(-2)=-4/9 and x(-1)=-1/3?
Sol: Taking Z-transform of both sides
Z[ 2x(n-2)-2x(n-1)+x(n)]=Z[3n-2 ]
Using the above equation of generalised form we get
2[z-2X(z)+z-1x(-1)+x(-2)]-3[z-1X(z)+x(-1)]+X(z)=3-2.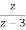 
Already given x(-2)=-4/9 and x(-1)=-1/3
Finally, substituting the values and solving above equation we get
X(z)=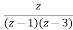
X(z)/z=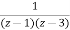
Now by partial fraction method we get
=
+ 
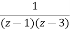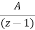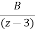
z=A(z-3)+B(z-1)
A+B=1
-3A-B=0
Solving above equations and finding A and B
A=-1/2 B=3/2
=
+ 
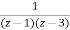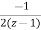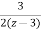
X(z)=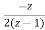
+ 
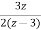
X(z)=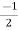
[
+ 
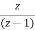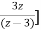
Taking inverse transform of above equation, we get (refer table of z-transform)
x[n]= 
[3n-1] n>0
Consider a system with hold circuit and closed loop system shown below.
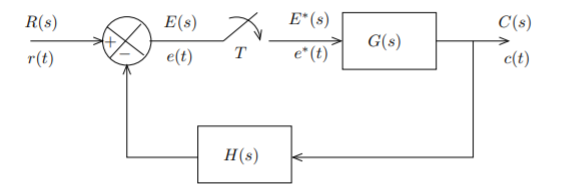
Fig: Closed loop system with hold circuit
The relation between input and output can be given as
E(s)=R(s)-G(s) H(s) E*(s)
C(s)=G(s)E*(s)
The pulse transform will then be
E*(s)=R*(s)-G*(s)H*(s)E*(s)
E*(s)=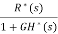
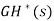=[G(s)H(s)]*
C(s)=G(s) E*(s)
=
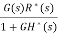
Taking pulse transform of above equation we get
C*(s)=[G(S)E*(s)]*
=
=
=
=
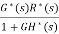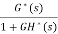
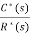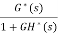
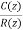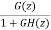
GH(z)=Z[G(s)H(S)]
The z-transfer function is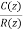 
=
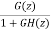
The pulse transfer function is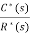 
=
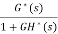
Pulse transfer function or z-transfer function characterizes the discrete data system responses only at sampling instants. The output information between the sampling instants is lost. Since the input of discrete data system is described by output of the sampler, for all practical purposes the samplers can be simply ignored and the input can be regarded as r∗(t).
The pulse transfer function relates the z-transform of the output to the z-transform of the input. Consider the following system where the system is subjected to digital signal r*(t).
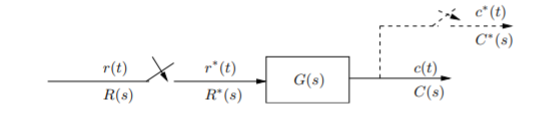
Fig: Sampled input system
The output is given as C(s)=G(s)R*(s)
From the above figure it is clear that the output is assumed to be c*(t). So, we can write the frequency domain function of the output as
C*(s)=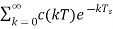
c(kT) is periodic we can again write,
C*(s)=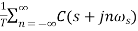
c(0)=0
Similarly, R*(s)=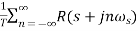
C*(s)=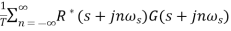
R*(s) is periodic. The above equation becomes
C*(s)=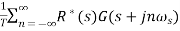
= R*(s)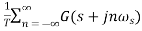
Let us suppose G*(s)=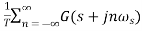
C*(s)= R*(s) G*(s)
G*(s)=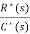
The above function is known as pulse transfer function.
G(z)=C(z)/R(z)
Then G(z) will be G(z)=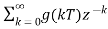
g(kT)= impulse response of g(t).
The transfer function of zero order hold is given as
Gho(s)=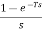
The pulse transfer function Gho(z)=Z[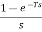
]
=(1-z-1)Z[1/s]
=(1-z-1)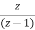
=1
The pulse transfer function is 1 because ZOH simply holds the discrete signal for one sampling period.
