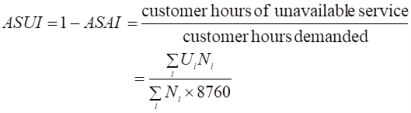Unit 6
Energy Control and Planning and Reliability of Power Systems
6.1.1 Interchange of power between interconnected utilities:
In some countries there are numerous, major electric utilities operating in parallel in three large AC interconnections. In many other parts of the world, simpler commercial structures of the electric power industry exist. Many countries have one to two major generation transmission utilities with local distribution utilities. The industry structure is important in discussing the interchange of power and energy since the purchase and sale of power and energy is a commercial business where the parties to any transaction expect to enhance their own economic positions under non emergency situations.
The market structures for electric energy and power are changing. In the past, interconnected electric utility systems dealt only with each other to buy and sell power and energy. Only occasionally did nonutility entities become involved, and these were usually large industrial organizations with their own generation. Many of these industrial firms had a need for process heat or steam and developed internal generation (i.e., cogeneration plants) to supply steam and electric power. Some developed electric power beyond the internal needs of the plant so that they could arrange for sale of the excess to the local utility system. The earlier markets only involved “wholesale transactions”, the sale and purchase of electric energy to utilities for ultimate delivery to the consumer. With the exception of industrial co-generators, all aspects of the interchange arrangements were made between interconnected utilities.
The movement towards more nonutility participation continues and more entities are becoming involved in the operation of the interconnected systems. Most all of the nonutility participants are involved in supplying power and energy to utilities or large industrial firms. The use of a transmission system by parties other than its owner may involve “wheeling” arrangements (that is, an arrangement to use the transmission system owned by another party to deliver power). There have been wheeling arrangements as long as there have been interconnections between more than two utilities. In most cases, the development of transmission service (i.e., wheeling) rates has been based on simplified physical models designed to facilitate commercial arrangements. As long as the market was restricted to a few parties, these arrangements were usually mutually satisfactory. With the introduction of nonutility participants, there is a need for the development of rate structures based on more realistic models of the power system.
The AGC scheme is an autonomous, local control based upon ACE. It is predicated (implicitly, at least) on the existence of a well-defined control area that usually corresponds to the geographical and electrical boundaries of one or more utilities. Interchanges are presumed to be scheduled between utility control centres so that the net interchange schedule is well defined and relatively stable over time. With many participants engaged in transactions and, perhaps, private generators selling power to entities beyond the local control area, the interchange schedule may be subject to more frequent changes and some local loads may no longer be the primary responsibility of the local utility. AGC systems may have to become more complex with more information being supplied in real time on all local generation, load substations, and all transactions. New arrangements may be needed to assign responsibility for control actions and frequency regulation. Utilities have done these tasks in the past out of their own self-interest. A new incentive may be needed as the need for frequency and tie-line control becomes a marketplace concern; not just the concern of the utility.
There are evolving market structures that include nonutility participants. These may include organizations that have generation resources, distributing utilities, and consumers, usually larger industrial firms. In these areas, we must venture into questions involving price. No transactions take place without involving prices, even those between utilities. Disputes naturally arise over what are fair price levels. (Price and fairness, like beauty, are in the eye of the beholder. The price level wanted for an older automobile may seem very fair to me as the seller and outrageous to the purchaser. We may both be correct and no sale will take place. Or one, or both, of us may be willing to change our views so that we do consummate a sale; in which case, the price agreed upon is “fair,” by definition.)
In areas where there is regulation of utility charges to consumers, prices are usually based on costs. (In most markets in capitalistic economies, prices are based on market action rather than being administered by governments.) There is usually a stated principal that utilities may recover no more than a given margin above “cost.” There may be some dispute over what costs should be included and how they should be allocated to each consumer class, but, generally, the notion of cost-based pricing is firmly established. Where utilities are dealing with each other or with nonutility entities, there may, or may not, be an obligation to base prices on costs. In many situations, market forces will set price levels. Transactions will be negotiated when both parties can agree upon terms that each considers advantageous, or at least satisfactory.
In the concept of wheeling, the delivery of power and energy over a transmission system (or systems) not owned by controlled by the generating entity or the purchasing entity. At the centre of the idea of selling transmission capacity to others is the definition and measurement of the available transmission capacity for transferring power.
6.1.2 Economy interchange evaluation:
Power systems interconnect because the interconnected system is more reliable, it is a better system to operate, and it may be operated at less cost than if left as separate parts. A load change in any of the systems is taken care of by all units in the interconnection, not just the units in the control area where the load change occurred. This fact also makes interconnections more reliable since the loss of a generating unit in one of them can be made up from spinning reserve among units throughout the interconnection. Thus, if a unit is lost in one control area, governing action from units in all connected areas will increase generation outputs to make up the deficit until standby units can be brought on-line. If a power system were to run in isolation and lose a large unit, the chance of the other units in that isolated system being able to make up the deficit are greatly reduced. Extra units would have to be
Run as spinning reserve, and this would mean less-economic operation. Furthermore, a generation system will generally require a smaller installed generation capacity reserve if it is planned as part of an interconnected system.
One of the most important reasons for interconnecting with neighbouring systems centres on the better economics of operation that can be attained when utilities are interconnected. This opportunity to improve the operating economics arises any time two power systems are operating with different incremental costs. As Example 10A will show, if there is a sufficient difference in the incremental cost between the systems, it will pay both systems to exchange power at an equitable price. To see how this can happen, one need merely reason as follows. Given the following situation:
- Utility A is generating at a lower incremental cost than utility B.
- If utility B were to buy the next megawatt of power for its load from utility A at a price less than if it generated that megawatt from its own generation, it would save money in supplying that increment of load.
- Utility A would benefit economically from selling power to utility B, as long as utility B is willing to pay a price that is greater than utility A’s cost of generating that block of power.
The key to achieving a mutually beneficial transaction is in establishing a “fair”price for the economy interchange sale.
There are other, longer-term interchange transactions that are economically advantageous to interconnected utilities. One system may have a surplus of power and energy and may wish to sell it to an interconnected company on a long-term firm-supply basis. It may, in other circumstances, wish to arrange to see this excess only on a “when, and if available” basis. The purchaser would probably agree to pay more for a firm supply (the first case) than for the interruptible supply of the second case.
Economy interchange evaluation:
Unless the two power systems have formed a power, pool or transmit this information to each other, or a third party, who will arrange the transaction; this assumption is incorrect. The most common situation involves system operations personnel, located in offices within each of the control areas, who can talk to each other by telephone. We can assume that each office has the data and computation equipment needed to perform an economic dispatch calculation for its own power system and that all information about the neighbouring system must come over the telephone (or some other communications network).
Way to coordinate the operations of the two power systems:
The simplest way to coordinate the operations of the two power systems is to note that if someone were performing an economic dispatch for both systems combined, the most economical way to operate would require the incremental cost to be the same at each generating plant, assuming that losses are ignored. The two operations offices can achieve the same result by taking the following steps:
1. Assume there is no interchange power being transmitted between the two systems.
2. Each system operations office runs an economic dispatch calculation for its own system.
3. By talking over the telephone, the offices can determine which system has the lower incremental cost. The operations office in the system with lower incremental cost then runs a series of economic dispatch calculations, each one having a greater total demand (that is, the total load is increased at each step). Similarly, the operations office in the system having higher incremental cost runs a series of economic dispatch calculations, each having a lower total demand.
4. Each increase in total demand on the system with lower incremental cost will tend to raise its incremental cost, and each decrease in demand on the high incremental cost system will tend to lower its incremental cost. By running the economic dispatch steps and conversing over the telephone, the two operations offices can determine the level of interchange energy that will bring the two systems toward most economic operation.
Under idealized “free market” conditions where both utilities are attempting to minimize their respective operating costs, and assuming no physical limitations on the transfer, their power negotiations (or bartering) will lead to the same economic results as a pool dispatch performed on a single area basis.
6.1.3 Interchange evaluation with unit commitment:
Assumption that conditions remained constant on the two power systems as the interchange is a good one if the interchange is to take place for a period of up to 1 h. However, there may be good economic reasons to transmit interchange power for periods extending from several hours to several days. Obviously, when studying such extended periods, we will have to take into account many more factors than just the relative incremental costs of the two systems.
Extended interchange transactions require that a model of the load to be served in each system (i.e., the expected load levels as a function of time) be included, as well as the unit commitment schedule for each.
The procedure for studying interchange of power over extended periods of time is as follows.
1. Each system must run a base-unit commitment study extending over the length of the period in question. These base-unit commitment studies are run without the interchange, each system serving its own load as given by a load forecast extending over the entire time period.
2. Each system then runs another unit commitment, one system having an increase in load, the other a decrease in load over the time the inter change is to take place.
3. Each system then calculates a total production cost for the base-unit commitment and for the unit commitment reflecting the effect of the interchange. The difference in cost for each system represents the cost of the interchange power (a positive change in cost for the selling system and a negative change in cost for the buying system). The price for the interchange can then be negotiated. If the agreed-on pricing policy is to “split the savings,” the price will be set by splitting the savings of the purchaser and adding the change in the cost for the selling system. If the savings are negative, it obviously would not pay to carry out the interchange contract.
The unit commitment calculation allows the system to adjust for the start-up and shut-down times to take more effective advantage of the interchange power. It may pay for one system to leave an uneconomical unit off-line entirely during a peak in load and buy the necessary interchange power instead.
6.1.4 Types of interchange:
There are other reasons for interchanging power than simply obtaining economic benefits. Arrangements are usually made between power companies to interconnect for a variety of reasons.
- Capacity Interchange:
Normally, a power system will add generation to make sure that the available capacity of the units it has equals its predicted peak load plus a reserve to cover unit outages. If for some reason this criterion cannot be met, the system may enter into a capacity agreement with a neighbouring system, provided that neighbouring system has surplus capacity beyond what it needs to supply its own peak load and maintain its own reserves. In selling capacity, the system that has a surplus agrees to cover the reserve needs of the other system. This may require running an extra unit during certain hours, which represents a cost to the selling system. The advantage of such agreements is to let each system schedule generation additions at longer intervals by buying capacity when it is short and selling capacity when a large unit has just been brought on-line and it has a surplus. Pure capacity reserve interchange agreements do not entitle the purchaser to any energy other than emergency energy requirements.
2. Diversity Interchange:
Daily diversity interchange arrangements may be made between two large systems covering operating areas that span different time zones. Under such circumstances, one system may experience its peak load at a different time of the day than the other system simply because the second system is 1 h behind. If the two systems experience such a phenomenon, they can help each other by interchanging power during the peak. The system that peaked first would buy power from the other and then pay it back when the other system reached its peak load.
This type of interchange can also occur between systems that peak at different seasons of the year. Typically, one system will peak in the summer due to air-conditioning load and the other will peak in winter due to heating load. The winter-peaking system would buy power during the winter months from the summer-peaking system whose system load is presumably lower at that time of year. Then in the summer, the situation is reversed and the summer-peaking system buys power from the winter-peaking system.
6.1.5 Energy Banking:
Energy-banking agreements usually occur when a predominantly hydro system is interconnected to a predominantly thermal system. During high water runoff periods, the hydro system may have energy to spare and will sell it to the thermal system. Conversely, the hydro system may also need to import energy during periods of low runoff. The prices for such arrangements are usually set by negotiations between the specific systems involved in the agreement.
Instead of accounting for the interchange and charging each other for the transactions on the basis of hour-by-hour operating costs, it is common practice in some areas for utilities to agree to a banking arrangement, whereby one of the systems acts as a bank and the other acts as a depositor. The depositor would “deposit” energy whenever it had a surplus and only the MWh “deposited” would be accounted for. Then, whenever the depositor needed energy, it would simply withdraw the energy up to MWh it had in the account with the other system. Which system is “banker” or “depositor”, this depends on the exchange contract. It may be that the roles are reversed as a function of the time of year.
6.1.6 Emergency Power Interchange:
It is very likely that at some future time a power system will have a series of generation failures that require it to import power or shed load. Under such emergencies, it is useful to have agreements with neighbouring systems that commit them to supply power so that there will be time to shed load. This may occur at times that are not convenient or economical from an incremental cost point of view. Therefore, such agreements often stipulate that emergency powerbe priced very high.
6.1.7 Inadvertent Power Exchange:
The AGC systems of utilities are not perfect devices with the result that there are regularly occurring instances where the error in controlling interchange results in a significant, accumulated amount of energy. This is known as inadvertent interchange. Under normal circumstances, system operators will “pay back” the accumulated inadvertent interchange energy megawatt-hour for megawatt-hour, usually during similar time periods in the next week. Differences in cost rates are ignored.
Occasionally, utilities will suffer prolonged shortages of fuel or water, and the inadvertent interchange energy may grow beyond normal practice. If done deliberately, this is known as “leaning on the ties.” When this occurs, systems will normally agree to pay back the inadvertent energy at the same time of day that the errors occurred. This tends to equalize the economic transfer. In severe fuel shortage situations, interconnected utilities may agree to compensate each other by paying for the inadvertent interchange at price levels that reflect the real cost of generating the exchange energy.
6.1.8 Power Pools:
Interchange of power between systems can be economically advantageous, as has been demonstrated previously. However, when a system is interconnected with many neighbours, the process of setting up one transaction at a time with each neighbour can become very time consuming and will rarely result in the optimum production cost. To overcome this burden, several utilities may forma power pool that incorporates a central dispatch office. The power pool is administered from a central location that has responsibility for setting up interchange between members, as well as other administrative tasks. The pool members relinquish certain responsibilities to the pool operating office in return for greater economies in operation.
The agreement the pool members sign is usually very complex. The complexity arises because the members of the pool are attempting to gain greater benefits from the pool operation and to allocate these benefits equitably among the members. In addition to maximizing the economic benefits of interchange between the pool members, pools help member companies by coordinating unit commitment and maintenance scheduling, providing a centralized assessment of system security at the pool office, calculating better hydro-schedules for member companies, and so forth. Pools provide increased reliability by allowing members to draw energy from the pool transmission grid during emergencies as well as covering each other’s reserves when units are down for maintenance or on forced outage.
A list of operating advantages for centrally dispatched power pools, ordered by greatest expected economic advantage, might look as follows:
1. Minimize operating costs (maximize operating efficiency).
2. Perform a system-wide unit commitment.
3. Minimize the reserves being carried throughout the system.
4. Coordinate maintenance scheduling to minimize costs and maximize reliability by sharing reserves during maintenance periods.
5. Maximize the benefits of emergency procedures.
There are disadvantages that must be weighed against these operating and economic advantages. Although it is generally true that power pools with centralized dispatch offices will reduce overall operating costs, some of the individual utilities may perceive the pool requirements and disciplines as disadvantageous. Factors that have been cited include.
1. The complexity of the pool agreement and the continuing costs of supporting the inter-utility structure required to manage and administer the pool.
2. The operating and investment costs associated with the central dispatch office and the needed communication and computation facilities.
3. The relinquishing of the right to engage in independent transactions outside of the pool by the individual companies to the pool office and the requirement that any outside transactions be priced on a split-saving basis based on pool members’ costs.
4. The additional complexity that may result in dealing with regulatory agencies if the pool operates in more than one state.
5. The feeling on the part of the management of some utilities that the pool structure is displacing some of an individual system’s management responsibilities and restricting some of the freedom of independent action possible to serve the needs of its own customers.
Power pools without central dispatch control centres can be administered through a central office that simply acts as a brokerage house to arrange transactions among members. In the opposite extreme, the pool can have a fully staffed central office with real-time data telemeter to central computers that calculate the best pool-wide economic dispatch and provide control signals to the member companies.
6.1.9 The Energy-Broker System:
As with sales and purchases of various commodities or financial instruments (e.g., stock), it is often advantageous for interconnected power systems to deal through a broker who sets up sales and purchases of energy instead of dealing directly with each other. The advantage of this arrangement is that the broker can observe all the buy and sell offers at one time and achieve better economy of operation. When utilities negotiate exchanges of power and energy in pairs, the “market place” is somewhat haphazard like a bazaar. The introduction of a central broker to accept quotations to sell and quotations to purchase creates an orderly marketplace where supply, demand, and prices are known simultaneously.
The simplest form of “broker” scheme is the “bulletin board.” In this type of scheme, the utility members post offers to buy or sell power and energy at regular, frequent intervals. Members are free to access the bulletin board (via some sort of data exchange network) at all times. Members finding attractive offers are free to contact those posting the offers and make direct arrangements for the transaction. Like any such informally structured market, many transactions will be made outside the marketplace. More complex brokers are those set up to arrange the matching of buyers and sellers directly, and, perhaps, to set transaction prices.
In one power broker scheme in use, the companies that are members of the broker system send hourly buy and sell offers for energy to the broker who matches them according to certain rules. Hourly, each member transmits an incremental cost and the number of megawatt-hours it is willing to sell or its decremental cost and the number of megawatt-hours it will buy. The broker sets up the transactions by matching the lowest cost seller with the highest cost buyer, proceeding in this manner until all offers are processed. The matched buyers and sellers will price the transaction on the basis of rules established in setting up the power broker scheme. A common arrangement is to compensate the seller for this incremental generation costs and split the savings of the buyer equally with the seller. The pricing formula for this arrangement is as follows.
Let
Fi = incremental cost of the selling utility (R/MWh)
FI, = decremental cost of the buying utility (R/MWh)
F, = cost rate of the transaction (R/MWh)
Then,
FC= F’S+ 
(F’b - F’S)
= F’S+ 
(F’b+ F’S)
In words, the transaction’s cost rate is the average of the seller’s incremental cost and the purchaser’s decremental cost. In this text, decremental cost is the reduction in operating cost when the generation is reduced a small amount.
6.1.10 Allocating Pool Savings:
All methods of allocating the savings achieved by a central pool dispatch are based on the premise that no pool member should have higher generation production expenses than it could achieve by dispatching its own generation to meet its own load.
Previously in the pool broker system that one of the ways to allocate pool savings is simply to split them in proportion each system’s net interchange during the interval. In the broker method of matching buyers and sellers based on their incremental and decremental costs, calculations of savings are relatively easy to make since the agreed incremental costs and amounts of energy must be transmitted to the broker at the start. When a central economic dispatch issued, it is easier to act as if the power were sold to the pool by the selling systems and then bought from the pool by the buying systems. In addition, allowances may be made for the fact that one system’s transmission system is being used more than others in carrying out the pool transactions.
Power system planning is a process in which the aim is to decide on new as well as upgrading existing system elements, to adequately satisfy the loads for a foreseen future. The elements may be Generation facilities, Substations, Transmission lines, and/or cables, Capacitors/Reactors, Etc.
The decision should be
• Where to allocate the element (for instance, the sending and receiving end of a line),
• When to install the element,
• What to select, in terms of the element specifications (for instance, number of bundles and conductor type).
Obviously, the loads should be adequately satisfied.
In the following subsections, some classifications of the subject are provided.
6.2.1 Need of short-term planning and long-term planning in generation:
- Static Versus Dynamic Planning:
Let us assume that our task is to decide on the subjects given above for 2015–2020.If the peak loading conditions are to be investigated, the studies involve six loading conditions. One way is to, study each year separately irrespective of the other years. This type of study is referred to as static planning which focuses on planning for a single stage. The other is to focus on all six stages, simultaneously, so that the solution is found for all six stages at the same time. This type of study is named as dynamic planning.
Obviously, although the static planning for a specific year provides some useful information for that year, the process as given above leads to impractical results for the period as the solutions for a year cannot be independent from the solution from the preceding years. One way to solve the problem is to include the results of each year in the studies for the following year. This may be referred to as semi-static, semi-dynamic, quasi-static or quasi-dynamic planning. It is apparent that the dynamic planning solution can be more optimal in comparison with the semi-static planning solution.
2. Transmission Versus Distribution Planning:
We may distinguish three main levels for a power system structure, namely, transmission, sub-transmission and distribution. Distribution level is often planned; or at least operated, radially. Figure 1 depicts a typical distribution network, starting from a 63 kV: 20 kV substations, ending to some types of loads, via both 20 kV and 400 V feeders. Note that switches A and B are normally open and may be closed if required. Switches C and D are normally closed and may be opened if required. A small generation is also connected to the network, as some types of local generations (named as Distributed Generations, or DGs) connected to the distribution systems, are of current industrial practices.
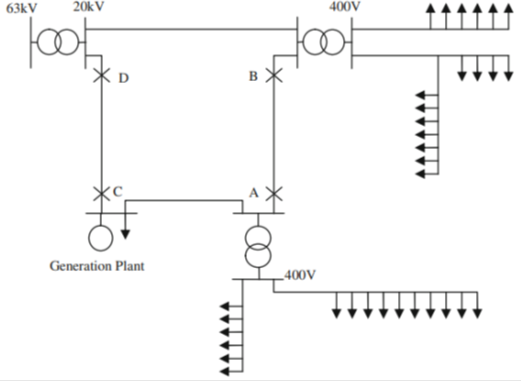
Fig.1. A typical radial distribution network
Looking at transmission and sub-transmission levels, these are generally interconnected. Normally both may be treated similarly, in terms of, the studies required and involved. From here on, with transmission, we mean both transmission and/or sub-transmission levels, except otherwise specified.
As seen, both transmission and distribution networks comprise of lines/cables, substations and generations. However, due to specific characteristic of a distribution system (such as its radial characteristics), its planning is normally separated from a transmission system. Although much of the ideas may be similar.
3. Long-term Versus Short-term Planning:
Power system planning issues may cover a period of 1–10 years, or even more. Suppose that, for the peak loading condition of the coming year, a power system utility expert notices that from the two lines, feeding a substation, one would be overloaded by 10% of its rating, while, the other would be loaded by 60% of its rating. After careful studies, he or she finds out that if a control device is installed on one line, the load distribution may be balanced on both lines. Once decided, the installation process of this device can be performed in such a way that no problem arises for the coming year. This is a typical short-term transmission planning decision.
Looking at the other extreme end, suppose that the load forecasting for the coming years shows that with all already available and planned generations, there would be a shortfall of generation in 9 years from now, onward. After a careful study, the planner decides on adding a new 2 9 500 MW steam power plant at a specific bus in that year. Its construction should start well in advance so that it would be available at the required time. His or her decision is a typical long-term (9-year) transmission planning decision.
There is no golden rule in specifying short-term or long-term planning issues. Normally, <1-year falls into the operational planning and operational issues in which the aim is typically to manage and operate available resources in an efficient manner. More than that falls into the planning stages. If installing new equipment and predicting system behaviour are possible in a shorter time (for instance, for distribution systems, 1–3 years), the term of short-term planning maybe used. More than that (3–10 years and even higher) is called long-term planning (typically transmission planning) in which predicting the system behaviour is possible for these longer periods. Moreover, installing a new element (such as a765 kV UHV line or a nuclear power plant) should be decided well in advance so that it would be available in due course.
6.2.2 Definition of reliability of power system
Introduction to power system reliability evaluation
Availability (AV) and forced outage rate (FOR)
Experience has shown that no machine is so reliable and dependable that it is available in successful operating condition all the time. That means that the machine needs to be off service (out of service) for maintenance or it may be off due to some other problems affecting its operation. As such, an off-service status includes planned outages and forced outages. Planned out ages(scheduled outages) are the ones when (a) unit(s) is purposely shutdown or taken out of service for maintenance or replacement. Forced outages are defined as the ones when (a) unit(s) is out of service due to failure (also called unscheduled or unplanned outage). The last one is the most severe and important factor in power system planning and operation and can be defined as
Forced outage rate (FOR) =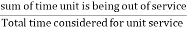 
FOR =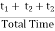 
Also, availability can be defined as
Availability AV =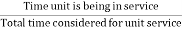 
And AV + FOR = 1.
The two terms “availability and forced outage rate” represent the probability of successful and failure event occurrence. According to the probability theory, it is known that the product AV1 X AV2 represents the probability that both unit 1 and unit 2 are simultaneously in operation during a specified interval of time, and, also,AV1X AV2 X AV3 means 1 and 2 and 3 are in operation at the same time, andFOR1X FOR2X FOR3 means that units 1, 2, and 3 are out of service in the same time.
Also, AV1X FOR2 means the probability that unit 1 is available (in service) and unit 2 is unavailable (out of service) in the same time.
For system generation reliability evaluation (including system expansion planning and/or systems interconnection), two models, namely, capacity model and load model, are needed; these are demonstrated and elaborated in the next two sections.
6.2.3 Load model:
The load model is known as the “load duration curve (LDC)” which is the most favourable one to be used instead of the regular load variation curve. There are some facts about the LDC that should be realized and can be summarized as follows:
a. The LDC is an arrangement of all load levels in a descending order of magnitude.
b. The area under the LDC represents the energy demanded by the system (consumed).
c. LDC can be used in economic dispatching, reliability evaluation, and power system planning and operation.
d. It is more convenient to deal with than the regular timely load variation curve.
The above discussion for the load duration curve is depicted in Figure 3 with all pertinent captions related to it.
6.2.4 Loss of load expectation (LOLE):
The LOLE risk index is the most widely accepted and utilized probabilistic method in power generation reliability evaluation for purposes of system expansion and interconnection. The two models, namely, the COPT and the LDC, mentioned in the preceding sections are convolved (combined) in the process. The unit of the LOLE is in days per year (d/y). The LOLE evaluation method is expressed in the following mathematical formula:
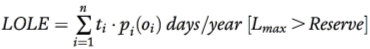
By observing the above equation, the LOLE would be applicable if, and only if, the maximum load (L max) exceeds the system reserve.
6.2.5 Expected energy not supplied (EENS):
Since power systems are in fact energy systems, the expected energy not supplied index may be deduced as per Figure 2. The ϵENS index is used in order to calculate energy sale, which is the real revenue for any electric company.
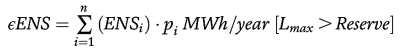
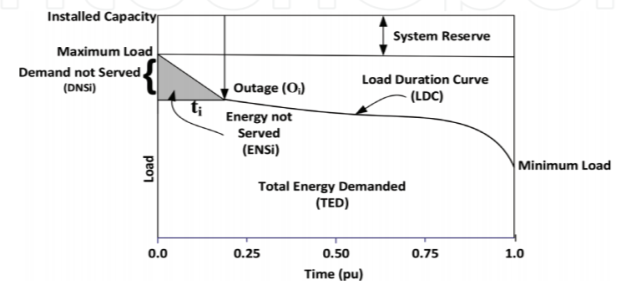
Fig.2. Load duration curve with energy not served.
6.2.6 Hierarchical levels for reliability study:
It has grown to be traditional within the field of power system reliability evaluation to divide the power system into 3 functional zones: generation, transmission, and distribution. It has been convenient to do so because utilities have traditionally been divided into these functional zones for purposes of organization, planning, operations and/or analysis. Although deregulation has affected the disaggregation of the traditional utility into many separated organizations, most of these organizations still have these corresponding internal divisions or are solely dedicated to the oversight of one of these functional zones.
• The main purpose of the functional zone division, in terms of reliability evaluation, is to provide a succinct means for identifying the part of the power system being analysed. It seems that we could evaluate any one functional zone, any combination of two of them, or all three simultaneously. Fig. 3 illustrates an organization of the functional zones by hierarchical levels, where the levels increase according to analysis complexity.
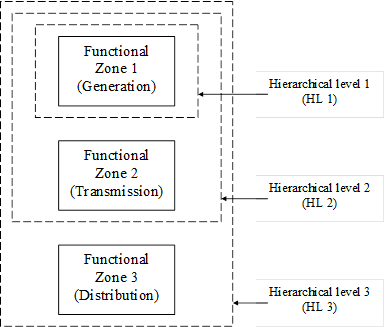
Fig. 3 Hierarchical levels
In HL-I evaluation, the reliability of the transmission is ignored, and the only concern is in estimating the necessary generating capacity to satisfy the system demand and to perform corrective and preventive maintenance on the generating units. Traditionally, this problem was handled in one of two ways:
• Require the reserve to be equal to or greater than a fixed percentage of either the installed capacity or the predicted load.
• Require the reserve to be equal to the capacity of the largest connected unit.
These deterministic methods for HL-I are still used today but have also been supplanted by probabilistic methods.
The above discussion applies to what is called single-area HL-I evaluation, which considers a single control area.
This approach can be extended to what is referred to as multi-area HL-I evaluation, where multiple control areas are considered together with the capacity of the transmission linkage between them. It is important to distinguish multi-area HL-I evaluation from HL-II evaluation:
• Multi-area HL-I: Model only the transmission links between areas. Account for the capacity of these links but not their possible failures.
• HL-II: Model entire transmission systems, including the capacity of each circuit and their possible failures.
Hierarchical level II
From Fig. 4, we see that hierarchical level II (HL-II) involves evaluation of two functional zones: generation and transmission. HL-II evaluation is commonly referred to as G&T, composite system, or bulk transmission system evaluation.
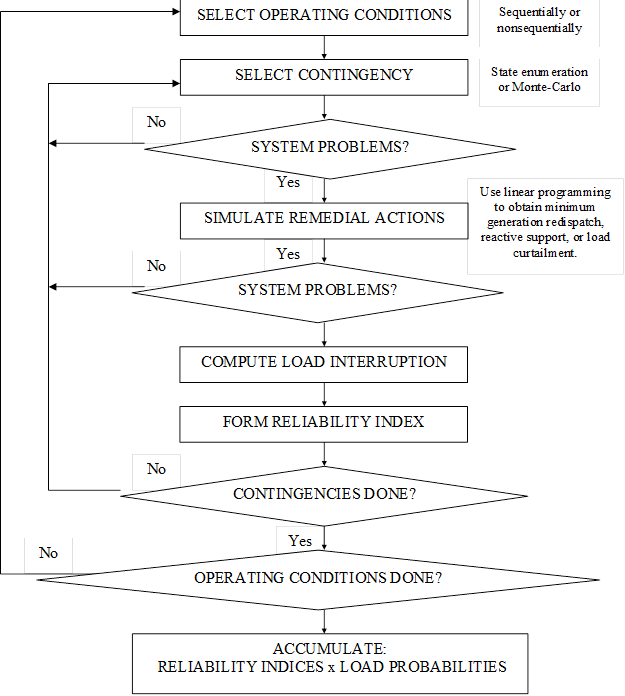
Fig.4 Generic HL-II Evaluation Algorithm
HL-II evaluation has been an extremely challenging problem for three basic reasons:
• Modelling: Models are required for
o failure/repair processes associated with generators, transformers, lines, and
Protection equipment,
o load
o effects of weather on failure/repair processes and load
o remedial actions including those of the operator
• Computations: It is necessary to achieve acceptable trade-off between speed and accuracy. A particularly intensive part of the computations involves determination of whether each state is a failure state or not.
• Data: This is an issue for any probabilistic analysis, but it is particularly troublesome for HL-II because data is required for characterizing failure rates of all equipment, and there are many difficulties associated with the related collection procedures.
Review of the literature reveals that most HL-II evaluation procedures are characterized by two attributes:
• Method of representing stochastic nature of the operating conditions:
By “operating conditions,” we are referring to the base case network configuration (topology and unit commitment) together with the loading and dispatch.
o Non sequential: The non sequential approach assumes a particular network configuration to be evaluated. Then several loading conditions are selected based on their occurrence probability (as indicated by a load duration curve), and for each chosen loading condition, the dispatch is developed through an economic dispatch calculation (or an equivalent market-dispatch tool). The evaluation is performed once for each loading condition, and then indices are computed as a function of the loading probabilities.
o Sequential: The sequential approach assumes a particular network configuration to be evaluated together with an hourly or daily peak load forecast for an extended time period (e.g., year or several years). The method then steps through a series of sequential-in-time operating conditions, evaluating the reliability indices at each step, with final indices an accumulation of those evaluated at each step. Each sequential evaluation performed is called a trajectory. It is possible to compute indices based on a single trajectory or based on multiple trajectories. In the latter case, Monte-Carlo simulation may be used to select the trajectory.
The advantage to non-sequential simulation is it is typically faster than sequential simulation. The advantage to sequential simulation is that it captures the effects of inter-temporal effects such as hydro-scheduling, maintenance, and unit commitment.
• Method of representing stochastic nature of contingencies:
o Contingency enumeration: Here, the “contingency states” corresponding to different numbers and combinations of outaged components are evaluated one by one, usually with some sort of intelligence to eliminate evaluation of some states.
o Monte-Carlo: Here, the “contingency states” evaluated are chosen as a result of random draw where the chance of drawing a particular state is the same as the probability of that state.
Hierarchical level III
Again, from Fig.4we see that hierarchical level III (HL-III) involves evaluation of all three functional zones, with modelling requirements starting at the generating points and terminating at the individual consumer load points. HL-III evaluations have not yet been carried out to any significant degree because
• There has been no decision problem with enough significance and occurrence frequency to drive its development, and
• Reliability assessment at HL-III poses significant challenges in modelling and computations.
Normally, therefore, the distribution functional zone is analysed as a separate entity.
6.2.7 State probabilities:
The probability of failing to satisfy the criterion of service adequacy and continuity can be evaluated. Provided the appropriate component reliability indices are known, it is relatively simple to evaluate the expected failure rate (λ) of the system, the average duration of the outage I, and the unavailability or annual outage time (µ). To do this, the values of λ, r, and µ are required for each component of the system.
The state-space transition diagram for a two-component system is shown in Figure 4.
The probability of a component being in the up state is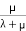
Also, the probability of a component being in the down state is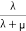
Probability of being in state 1=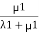 
.
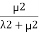
Probability of being in state 2=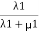
.
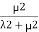
Probability of being in state 3=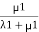
.
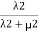
Probability of being in state 4=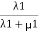
.
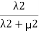
He most accurate method for analysing networks including weather states is to use the Markov modelling. However, this becomes impractical for all except the simplest system. Instead, therefore, an approximate method is used based upon simple rules of probability.
6.2.8 Distribution system reliability evaluation for radial and parallel system
Series components (Radial System):
The requirement is to find the reliability indices of a single component that is equivalent to a set of series-connected components as shown in Figure 5.
If the components are in series from a reliability point of view, both must operate, i.e., be in upstate, for the system to be successful, i.e., the upstate of a series system is state 1 of the state-space diagram shown in Figure 5.
From the above equation (state 1), the probability of being in this upstate is
In addition, since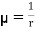
, the above equation becomes
rs =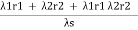 
=
=
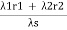
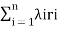
Also, the rate of transition from state 1 of the two-component state-space
Diagram is λ1 + λ2, therefore
Fig. 5 State-space diagram for two-component system.
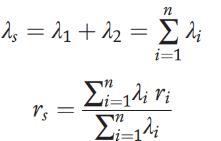
Thus, the unavailability for series systems (µS) can be expressed as
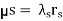
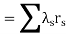
In particular, the order of evaluation is usually
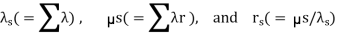
Although these equations were derived from the assumption of exponential distribution, they are expected or average values and can be shown to be valid irrespective of the distribution assumption.
Parallel components:
Many systems consist of both series and parallel connections. These systems can be seen in transmission lines, in combinations of transformers, cables, feeders, relays, protection and control devices, etc. As an example, Figure 6 displays two parallel lines that are both connected in series with another line. In these situations, and from a reliability point of view, it is essential to consequently reduce the network in order to estimate its overall reliability. This is accomplished by repeatedly combining sets of parallel and series components into equivalent network components until a single component remains. The reliability of the last component is equal to the reliability of the original system (Figure 6).
In this case, the requirement is to find the indices of a single component that is equivalent to two parallel components as shown in Figure 6.If the components are in parallel from a reliability point of view, both must fail for resulting in a system failure, the probability of being in this downstate is
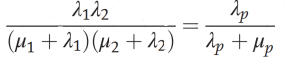
Also, the rate of transition from state 4 of the two-component state-space diagram is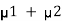
, Therefore 
.
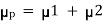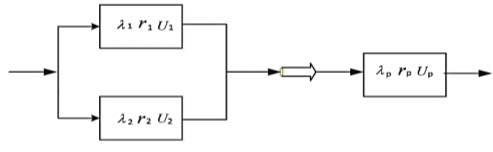
Fig. 6 State-space diagram for a two-component system. (Parallel)
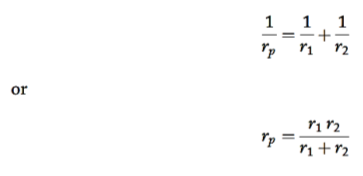
From the above equations, it yields that
=
= 
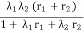
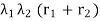
Thus, the unavailability for parallel systems µpcan be expressed as
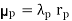
In practice, the order of evaluation is usually,
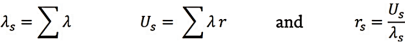
Although these equations were derived from the assumption of exponential distribution, they are expected or average values and can be shown to be valid irrespective of the distributional assumption.
6.2.9 Customer-based reliability indices:
The most widely used reliability indices are averages that weight each customer equally. Customer-based indices are popular with electric companies, since a small residential customer has just as much importance as a large industrial customer. Regardless of the limitations they have, these are generally considered acceptable techniques showing adequate measures of reliability. Indeed, they are often used as reliability benchmarks and improvement targets. The formulae for customer-based indices include:
• SAIFI, system average interruption frequency index:
SAIFI is a measure of how many sustained interruptions an average customer will experience over the course of a year. This measure can be defined as,
Where λi is the failure rate at load point i
And Ni is the number of customers at load point i.
• CAIFI, customer average interruption frequency index:
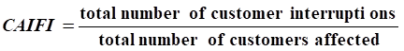
Where this index differs from SAIFI only in the denominator, where here, we count only those customers affected rather than total customers. In application of this index, customers affected should be counted only once, independent of the number of times they are interrupted.
• SAIDI, system average interruption duration index, given by:
Where Ui is the annual outage time at load point i.
SAIDI is a measure of how many interruption hours an average customer will experience over the course of a year. For a fixed number of customers, SAIDI can be improved by reducing the number of interruptions or by reducing the duration of these interruptions. Since both of these reflect reliability improvements, a reduction in SAIDI indicates an improvement in reliability.
• CAIDI, customer average interruption duration index:
CAIDI is a measure of how long an average interruption lasts and is used as a measure of utility response time to the system contingencies. CAIDI can be improved by reducing the length of interruptions but can also be reduced by increasing the number of short interruptions. Consequently, a reduction in CAIDI does not necessarily reflect an improvement in system reliability.
• ASAI, average service availability index:
ASAI is the customer-weighted availability of the system and provides the same information as SAIDI. Higher ASAI values reflect higher levels of system reliability.
• ASUI, average service unavailability index:
