Unit 1

Design of combinational circuit

1.1 Booleans algebra

Theorems and Properties of Boolean Algebra:

• It deals with binary numbers & variables.
• Therefore, also known as Binary Algebra or logical Algebra.
• A mathematician named George Boole had developed this algebra in 1854.
• The variables that are used in this algebra are known as Boolean variables.
• Considering the range of voltages as logic ‘High’ is represented with ‘1’ and logic ‘Low’ is represented with ‘0’.

Postulates and Basic Laws of Boolean Algebra

Here, the Boolean postulates and basic laws that are used are given underneath.

Boolean Postulates

• Considering the binary numbers 0 and 1, boolean variable (x) and its complement (x’).
• They are known as literal.
• The possible logical OR operations are:

x + 0 = x

x + 1 = 1

x + x = x

x + x’ = 1

• Similarly, the possible logical AND operations are:

x.1 = x

x.0 = 0

x.x = x

x.x’ = 0

• These are the simple Boolean postulates and verification can be done by substituting the Boolean variable with ‘0’ or ‘1’.

Basic Laws of Boolean Algebra

• The three basic laws of Boolean Algebra are:

• Commutative law
• Associative law
• Distributive law

Commutative Law

• The logical operation carried between two Boolean variables when gives the same result irrespective of the order the two variables, then that operation is said to be Commutative. The logical OR & logical AND operations between x & y are shown below

x + y = y + x

x.y = y.x

• The symbol ‘+’ and ‘.’ indicates logical OR operation and logical AND operation.
• Commutative law holds good for logical OR & logical AND operations.

Associative Law

• If a logical OR operation of any two Boolean variables is performed first and then the same operation is performed with the remaining variable providing the same result, then that operation is said to be Associative. The logical OR & logical AND operations of x, y & z are:

x + (y + z) = (x + y) + z

x.(y.z) = (x.y).z

• Associative law holds good for logical OR & logical AND operations.

Distributive Law

• If a logical OR operation of any two Boolean variables is performed first and then AND operation is performed with the remaining variable, then that logical operation is said to be Distributive. The distribution of logical OR & logical AND operations between variables x, y & z are :

x.(y + z) = x.y + x.z

x + (y.z) = (x + y).(x + z)

• Distributive law holds good for logical OR and logical AND operations.
• These are the Basic laws of Boolean algebra and we can verify them by substituting the Boolean variables with ‘0’ or ‘1’.

Theorems of Boolean Algebra

• The following theorems are used in Boolean algebra.
  • Duality theorem
  • De Morgan’s theorem

Duality Theorem

• It states that “The dual of the Boolean function is obtained by interchanging the logical AND operator with logical OR operator and zeros with ones”.
• For every Boolean function, there is a Dual-function.
• Let us make the Boolean equations (relations) of Boolean postulates and basic laws into two groups. The following table shows these two groups.

• Every row comprises two Boolean equations and they are dual to one other.
• We can also verify the Boolean equations of Group1 and 2 by using the duality theorem.

Simplification of Boolean Functions

Numerical

• Simplify the Boolean function,

f = p’qr + pq’r + pqr’ + pqr

Method 1

Given

f = p’qr + pq’r + pqr’ +pqr.

In the first and second terms, r is common and in third and fourth terms pq is common.

So, taking out the common terms by using Distributive law we get,

⇒ f = (p’q + pq’)r + pq(r’ + r)

The terms present in the first parenthesis can be simplified by using the Ex-OR operation.

The terms present in the second parenthesis is equal to ‘1’ using Boolean postulate we get

⇒ f = (p ⊕q)r + pq(1)

The first term can’t be simplified further.

But, the second term is equal to pq using Boolean postulate.

⇒ f = (p ⊕q)r + pq

Therefore, the simplified Boolean function is f = (p⊕q)r + pq

Method 2

Given f = p’qr + pq’r + pqr’ + pqr.

Using the Boolean postulate, x + x = x.

Hence we can write the last term pqr two more times.

⇒ f = p’qr + pq’r + pqr’ + pqr + pqr + pqr

Now using the Distributive law for 1st and 4th terms, 2nd and 5th terms, 3rdand 6th terms we get.

⇒ f = qr(p’ + p) + pr(q’ + q) + pq(r’ + r)

Using Boolean postulate, x + x’ = 1 and x.1 = x for further simplification .

⇒ f = qr(1) + pr(1) + pq(1)

⇒ f = qr + pr + pq

⇒ f = pq + qr + pr

Therefore, the simplified Boolean function is f = pq + qr + pr.

Hence we got two different Boolean functions after simplification of the given Boolean function. Functionally, these two functions are the same. As per requirement, we can choose one of them.

Numerical

Find the complement of the Boolean function,

f = p’q + pq’.

Solution:

Using DeMorgan’s theorem, (x + y)’ = x’.y’ we get

⇒ f’ = (p’q)’.(pq’)’

Then by second law, (x.y)’ = x’ + y’ we get

⇒ f’ = {(p’)’ + q’}.{p’ + (q’)’}

Then by using, (x’)’=x  we get

⇒ f’ = {p + q’}.{p’ + q}

⇒ f’ = pp’ + pq + p’q’ + qq’

Using x.x’=0 we get

⇒ f = 0 + pq + p’q’ + 0

⇒ f = pq + p’q’

Therefore, the complement of Boolean function, p’q + pq’ is pq + p’q’.

1.2 De-Morgan theory

• It is useful in finding the complement of the Boolean function.
• It states that “The complement of logical OR of at least two Boolean variables is equal to the logical AND of each complemented variable”.
• It can be represented using 2 Boolean variables x and y as

(x + y)’ = x’.y’

• The dual of the above Boolean function is

(x.y)’ = x’ + y’

• Therefore, the complement of logical AND of the two Boolean variables is equivalent to the logical OR of each complemented variable.
• Similarly, DeMorgan’s theorem can be applied for more than 2 Boolean variables also.

1.3 Karnaugh map: structure for two, three, and four Variables

KARNAUGH MAP

• Karnaugh introduced a method for simplification of Boolean functions in a very easy way.
• This method is known as the Karnaugh map method or K-map method.
• It is a graphical method, which comprises 2n cells for ‘n’ variables.
• Here, the adjacent cells vary only in a single bit position.

2 Variable K-Map

It has 4 number of cells since the number of variables is two.

The 2 variable K-Map is :

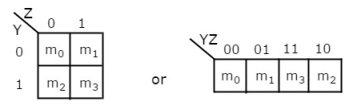
Fig: 2 variable K-Map (ref. 1)

• The only way to group 4 adjacent min terms.
• The possible combinations are {(m0, m1), (m2, m3), (m0, m2) and (m1, m3)}.

3 Variable K-Map

It has 8 number of cells since the number of variables is 3.

The 3 variable K-Map is:

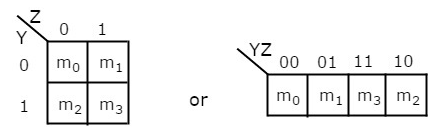
Fig: 3 variable K-Map

• The only way to group 8 adjacent min terms.
• The possible are {(m0, m1, m3, m2), (m4, m5, m7, m6), (m0, m1, m4, m5), (m1, m3, m5, m7), (m3, m2, m7, m6) and (m2, m0, m6, m4)}.
• The possible combinations of grouping 2 adjacent min terms are {(m0, m1), (m1, m3), (m3, m2), (m2, m0), (m4, m5), (m5, m7), (m7, m6), (m6, m4), (m0, m4), (m1, m5), (m3, m7) and (m2, m6)}.
• If x=0, then 3 variable K-map becomes 2 variable K-map.

4 Variable K-Map

It has 16 numbers of cells since the number of variables is 4.

The 4 variable K-Map is:

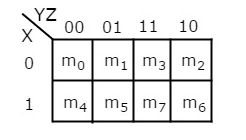
Fig: 4 variable K-Map

• The only way to group 8 adjacent min terms.
• Let R1, R2, R3, and R4 represent the min terms of the first row, second row, third row, and fourth row respectively.
• Similarly, C1, C2, C3, and C4 represent the min terms of the first column, second column, third column, and fourth column respectively.
• The possible combinations are {(R1, R2), (R2, R3), (R3, R4), (R4, R1), (C1, C2), (C2, C3), (C3, C4), (C4, C1)}.
• If w=0, then 4 variable K-map becomes 3 variable K-map.

Rules for simplifying K-maps:

• Selecting K-map based on the number of variables present in the Boolean function.
• If the Boolean function is in Max terms form, then place the zeroes at respective Max term cells in the K-map.
• If the Boolean function is in PoS form, then place the zeroes wherever required in K-map for which the given sum terms are valid.
• The maximum possibilities of grouping are checked for adjacent zeroes.
• It should be of powers of two.
• Starting from the highest power of two and to the least power of two.
• The highest power is equivalent to the number of variables considered in K-map and the least power is zero.
• Each group will give either a literal or one sum term.
• It is known as prime implicant.
• The prime implicant is an essential prime implicant when at least a single ‘0’ is not covered with any other groups but only that grouping covers.
• The simplified Boolean function contains all essential prime implicants and only the required prime implicants.

Numericals

Simplify  f(X,Y,Z)=∏M(0,1,2,4)f(X,Y,Z)=∏M(0,1,2,4)using K-map.

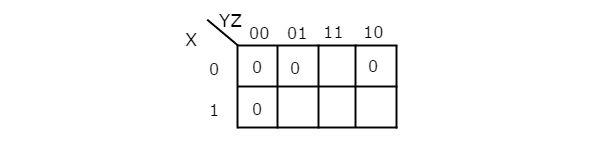
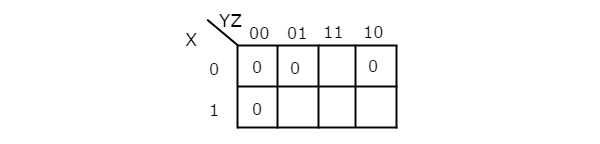
Therefore, the simplified Boolean function is

f = (X + Y).(Y + Z).(Z + X)

Simplify:

F(P,Q,R,S)=∑(0,2,5,7,8,10,13,15)

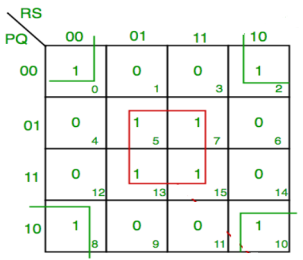
F = P’Q’R’S’ + PQ’R’S’ + P’Q’RS’ +PQ’RS’ + QS

F = P’Q’S’ + PQ’S’ + QS

F = Q’S’ +QS

Simplify:

F(A,B,C)=π(0,3,6,7)

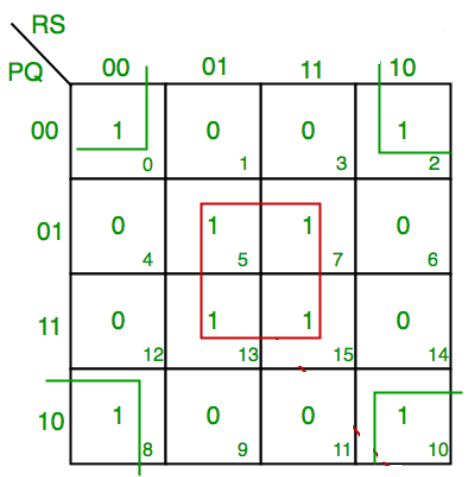
F = A’BC +ABC +A’B’C’ +ABC’

F = BC + C’ ( A’B’ + AB )

Key Takeaways:

• K-map is a graphical method, which comprises 2n cells for ‘n’ variables.
• It is a method for simplification of Boolean functions in a very easy way.
• It is used for 5 variables at the max.

1.4 SOP, and POS form reduction of Boolean expressions by K-map

Reduction rules for SOP using K-map

There are a couple of rules that we use to reduce SOP using K-map . There are some rules for this :

Pair reduction Rule

Consider the following 4 variables K-map

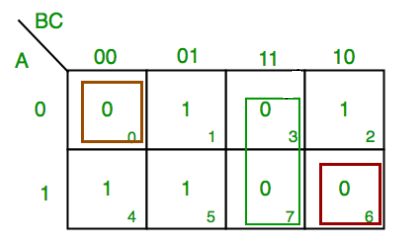
Now we mark the cells in pair (set of 2) having value 1.

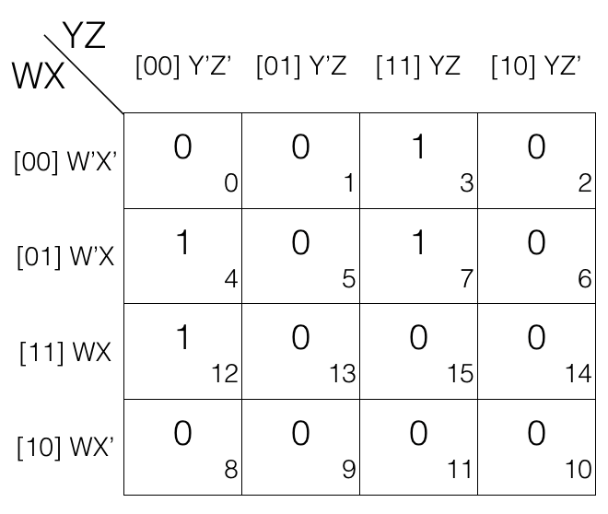
The 1st pair = W’XY’Z’ + WXY’Z’
the 2nd pair = W’X’YZ + W’XYZ
(the pairs are in Sum of Products SOP form)

Now we will remove the variable that changed in the 1st and 2nd pair. Looking at the 1st pair W’ changed to W so we remove it. And looking at the 2nd pair X’ changed to X so we remove it.

So the updated pairs after reduction are given below.
1st pair
= W’XY’Z’ + WXY’Z’
= XY’Z’

2nd pair
= W’X’YZ + W’XYZ
= W’YZ

Note!
Pair reduction rule removes 1 variable.

Quad reduction Rule

Consider the following 4 variables K-map.

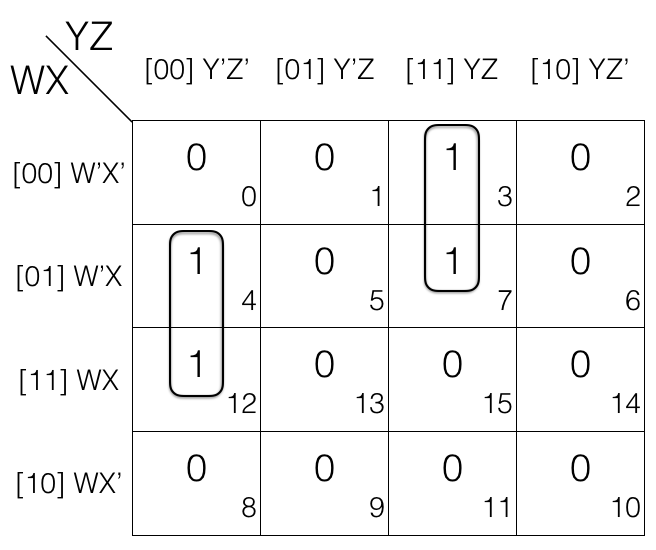
Mark the cells in quad (set of 4) having value 1.

The 1st quad = W’X’Y’Z’ + W’XY’Z’ + WXY’Z’ + WX’Y’Z’
The 2nd quad = W’X’YZ + W’XYZ + W’X’YZ’ + W’XYZ’
(the quads are in Sum of Products SOP form)

Now we will remove the variable that changed in the 1st and 2nd quad.

Looking at the 1st quad W’ and X’ changed to W and X so, we remove them. And looking at the 2nd quad X’ and Z changed to X and Z’ so, we remove them.

So the updated quads after reduction.

1st quad
= (W’X’Y’Z’ + W’XY’Z’) + (WXY’Z’ + WX’Y’Z’)
= W’Y’Z’ + WY’Z’
= Y’Z’

2nd quad
= (W’X’YZ + W’XYZ) + (W’X’YZ’ + W’XYZ’)
= W’YZ + W’YZ’
= W’Y

Note!
quad reduction rule removes 2 variables.

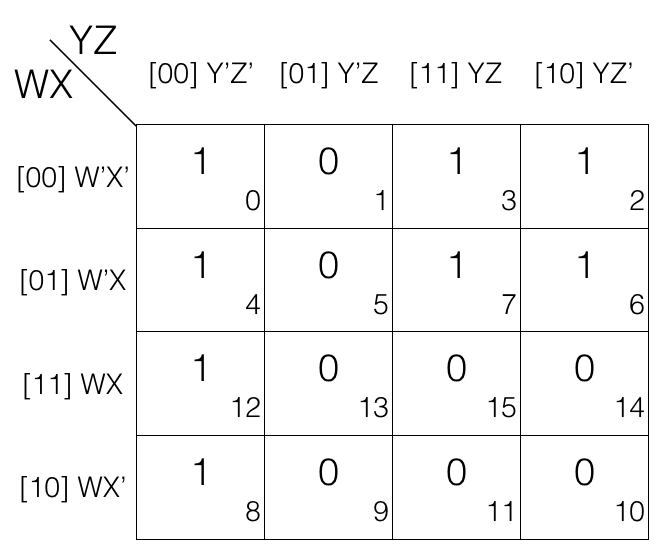
Octet reduction Rule

Consider the following 4 variables K-map.

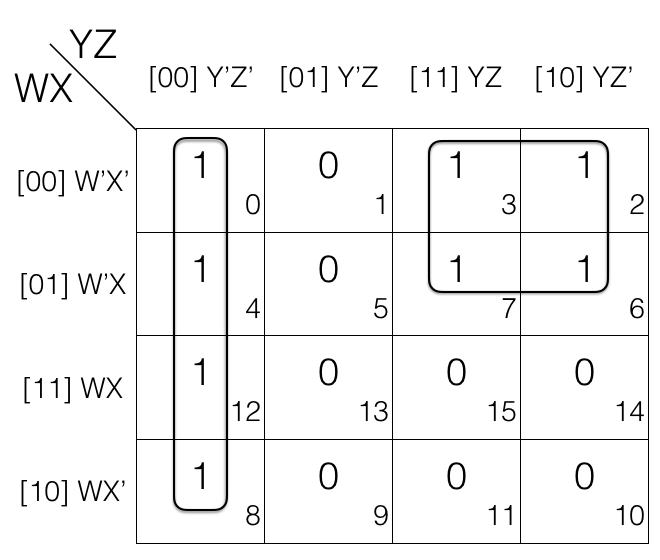
Mark the cells in octet (set of 8) having value 1.

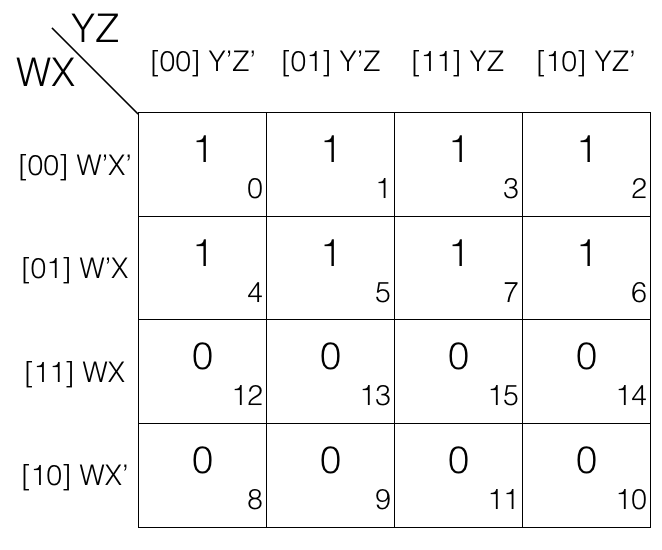
Octet = W’X’Y’Z’ + W’X’Y’Z + W’X’YZ + W’X’YZ’ + W’XY’Z’ + W’XY’Z + W’XYZ + W’XYZ’
(the octet is in Sum of Products SOP form)

Now we will remove the variable that changed in the octet. Looking at the octet moving top to bottom: X’ changed to X. Moving from left to right: Y’ changed to Y. Moving from left to right: Z’ changed to Z.

Updated octet after reduction
octet
= (W’X’Y’Z’ + W’X’Y’Z) + (W’X’YZ + W’X’YZ’) + (W’XY’Z’ + W’XY’Z) + (W’XYZ + W’XYZ’)
= (W’X’Y’ + W’X’Y) + (W’XY’ + W’XY)
= W’X’ + W’X
= W’

Note!
octet reduction rule will remove 3 variables.

Map Rolling reduction Rule

In this we consider that the K-map top edge is connected with the bottom edge and left edge is connected with the right edge. Then we mark the pairs, quads and octets. Lets check few examples.

Map Rolling reduction Rule - marking the pairs

Consider the following 4 variables K-map

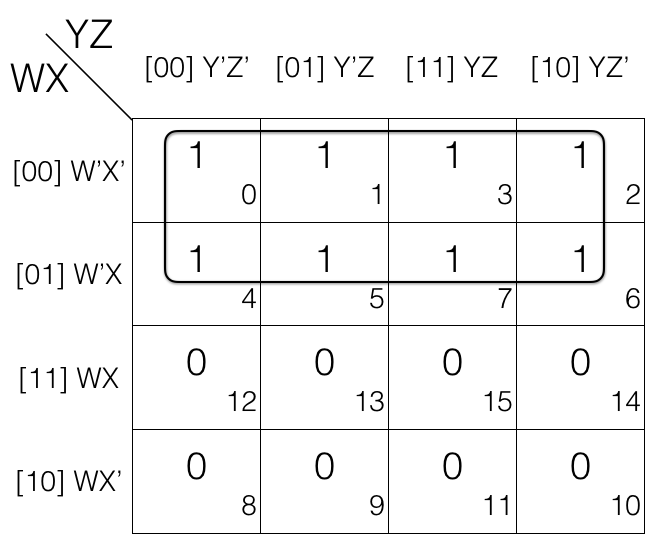
In the above k-map we have rolled it and then marked the pairs.

1st pair = W’X’Y’Z + WX’Y’Z
2nd pair = WXY’Z’ + WXYZ’

In 1st pair W’ change to W and in 2nd pair Y’ change to Y. So we will remove them.

Updated pairs after reduction
1st pair
= W’X’Y’Z + WX’Y’Z
= X’Y’Z

2nd pair
= WXY’Z’ + WXYZ’
= WXZ’

Map Rolling reduction Rule - marking the quads

Consider the following 4 variables K-map

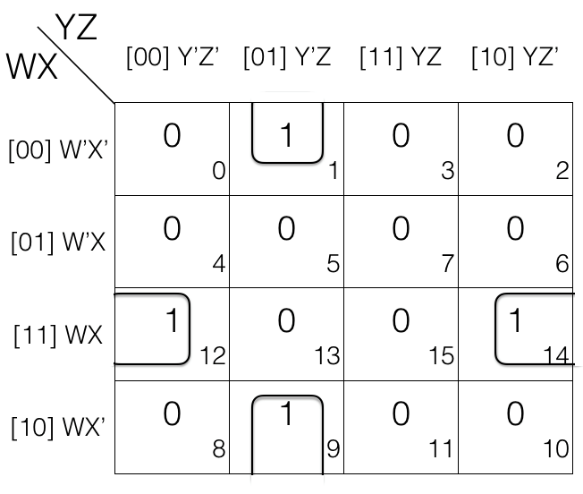
In the above k-map we have rolled it and then marked the quads.

1st quad
= W’X’Y’Z + W’X’YZ + WX’Y’Z + WX’YZ

2nd quad
= W’XY’Z’ + WXY’Z’ + W’XYZ’ + WXYZ’

In 1st quad and 2nd quad W’ change to W and Y’ changes to Y. So we will remove them.

Updated quads after reduction

1st quad
= (W’X’Y’Z + W’X’YZ) + (WX’Y’Z + WX’YZ)
= W’X’Z + WX’Z
= X’Z

2nd quad
= (W’XY’Z’ + WXY’Z’) + (W’XYZ’ + WXYZ’)
= XY’Z’ + XYZ’
= XZ’

Map Rolling reduction Rule - marking the octets

Consider the following 4 variables K-map

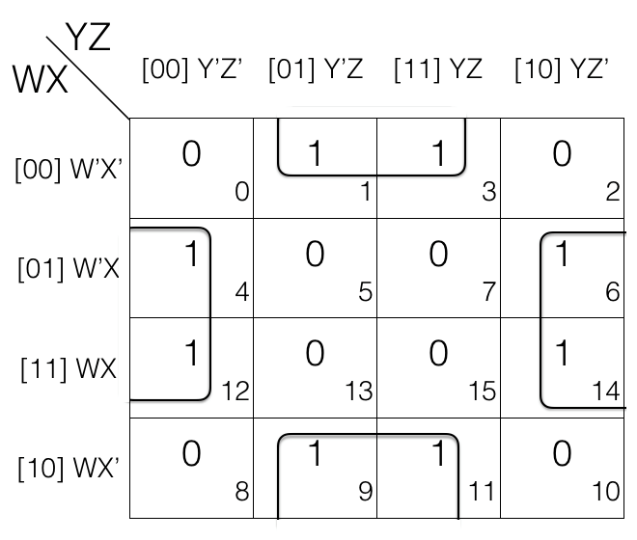
In the above k-map we have rolled it and then marked the octet.

Octet
= W’X’Y’Z’ + W’X’Y’Z + W’X’YZ + W’X’YZ’ + WX’Y’Z’ + WX’Y’Z + WX’YZ + WX’YZ’

Looking at the octet we can tell that W’ changed to W, Y’ changed to Y and Z’ changed to Z. So we will remove them.

Updated octet after reduction

octet
= (W’X’Y’Z’ + W’X’Y’Z) + (W’X’YZ + W’X’YZ’) + (WX’Y’Z’ + WX’Y’Z) + (WX’YZ + WX’YZ’)
= (W’X’Y’ + W’X’Y) + (WX’Y’ + WX’Y)
= W’X’ + WX’
= X’

Overlapping Groups

When a value in a cell of K-map is encircled in more that one group (pair, quad or octet) then we call such groups an overlapping groups. Lets check an example.

Consider the following 4 variables K-map.

1st pair = W’XY’Z’ + W’XY’Z
= m4 + m5

2nd pair = WXYZ + WXYZ’
= m15 + m14

quad = W’XY’Z + W’XYZ + WXY’Z + WXYZ
= m5 + m7 + m13 + m15

If we look at m5 and m15, they are overlapping.

Overlapping groups helps in getting simpler expression after reduction.

Updated pair and quad after reduction

1st pair = W’XY’Z’ + W’XY’Z
= W’XY’

2nd pair = WXYZ + WXYZ’
= WXY

quad = W’XY’Z + W’XYZ + WXY’Z + WXYZ
= W’XZ + WXZ
= XZ

Redundant Groups

After marking out the overlapping groups it is important to also check for redundant groups. If all the values of a group G (pair, quad or octet) is covered (overlapping) with other groups then that group G is redundant and ignored. Lets check an example.

Consider the following 4 variables K-map.

1st pair = W’XY’Z + W’XYZ = m5 + m7

2nd pair = WXY’Z’ + WXY’Z = m12 + m13

3rd pair = W’XY’Z + WXY’Z = m5 + m13

If we look at m5 and m13 i.e. 3rd pair, it is a redundant group as m5 and m13 is covered in 1st and 2nd pair so we will remove the redundant group (3rd pair).

Updated pairs after reduction

1st pair = W’XY’Z + W’XYZ
= W’XZ

2nd pair = WXY’Z’ + WXY’Z
= WXY’

Summary of Reduction rules for SOP using K-map

1. Prepare the truth table for the function
2. Draw an empty K-map (2-variables, 3-variables, so on)
3. Fill the cells with value 1 for which the output is 1
4. Fill rest of the cells with value 0
5. Mark the Octets, Quads and Pairs by encircling the value 1s (also check map rolling, overlapping groups and remove redundant groups)
6. Write the final reduced expression and OR (+) them to get the answer

Now let us solve a problem.

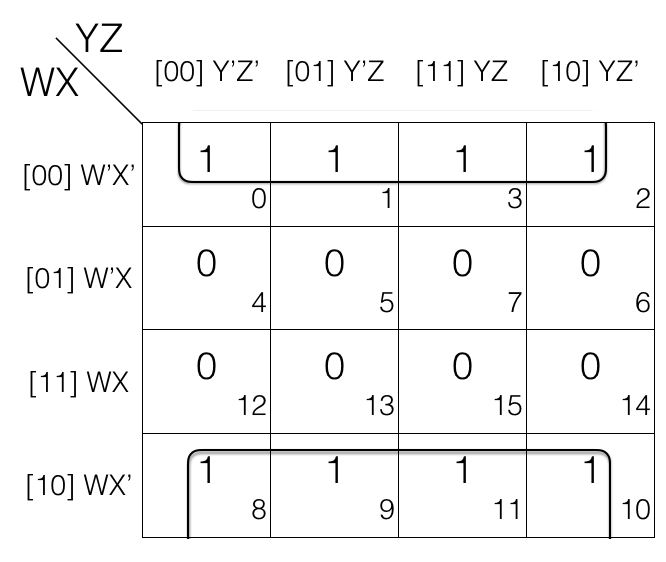
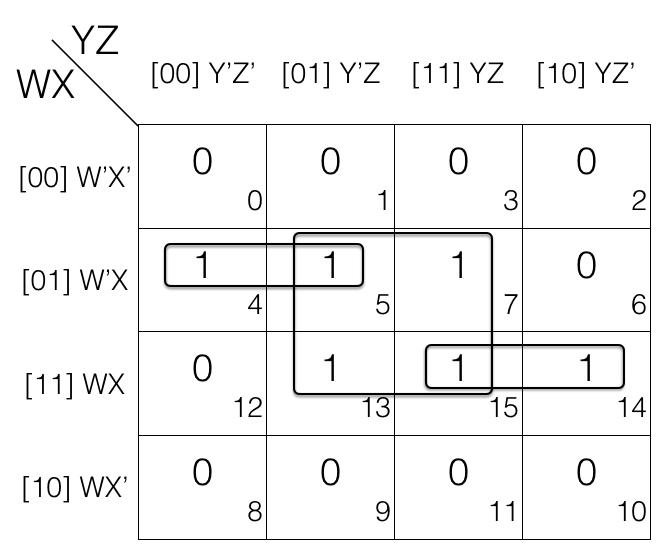
Reduce F(A,B,C,D) = ∑(0,1,2,4,5,7,10,15) using K-map

Since function F has 4 variables so we will create a 4 variable K-map having 24 = 16 cells.

Now fill the cell marked with subscript 0,1,2,4,5,7,10 and 15 with value 1 as we are dealing with Sum of Products SOP.

And fill rest of the cells with value 0

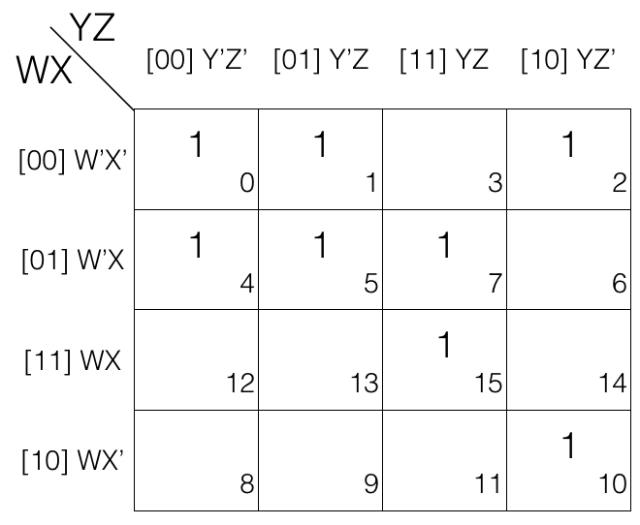
Now we will mark the octets, quads and pairs.

Looking at the K-map we can tell that there is no octets so we will look for quads.

The k-map has quad so we will mark it.

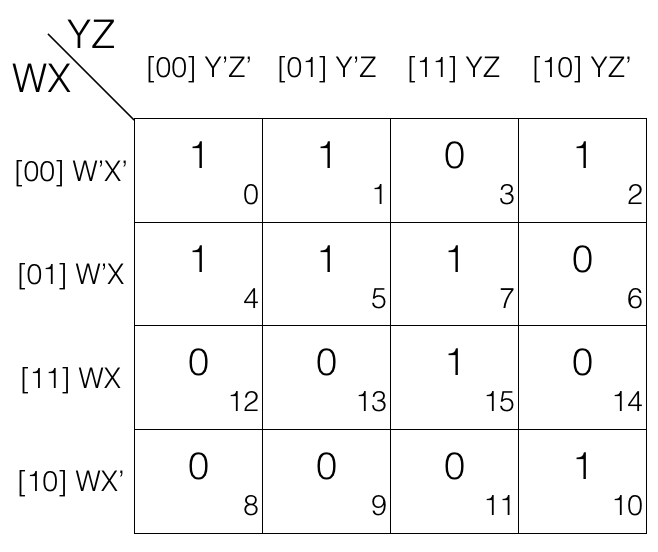
Now we will look for pairs. If we look close we can tell that the k-map has some pairs. So we will mark them.

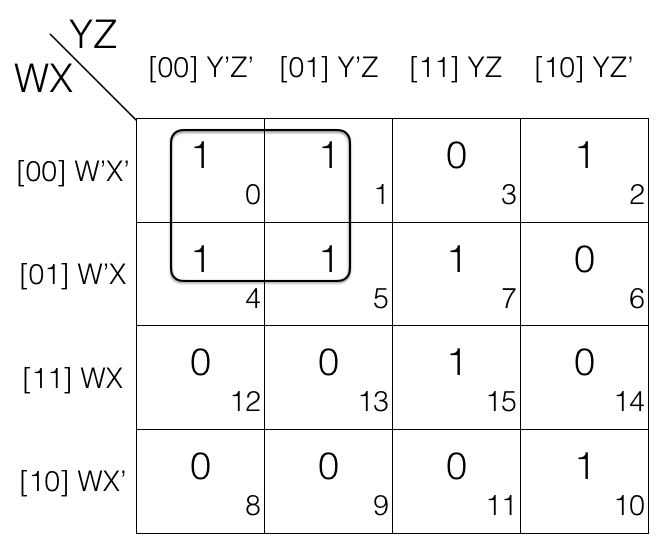
Now we will map-roll and look for octets. If we look at the k-map we can tell that after map rolling we don't get any octet. So we will now check for quads.

We roll the k-map again and this time we are looking for quads. But giving a closer look we can tell that there is no quad after we do map rolling. So time for us to look for pairs.

Looking closer we can tell that after map rolling the k-map we have a pair. So we will mark it.

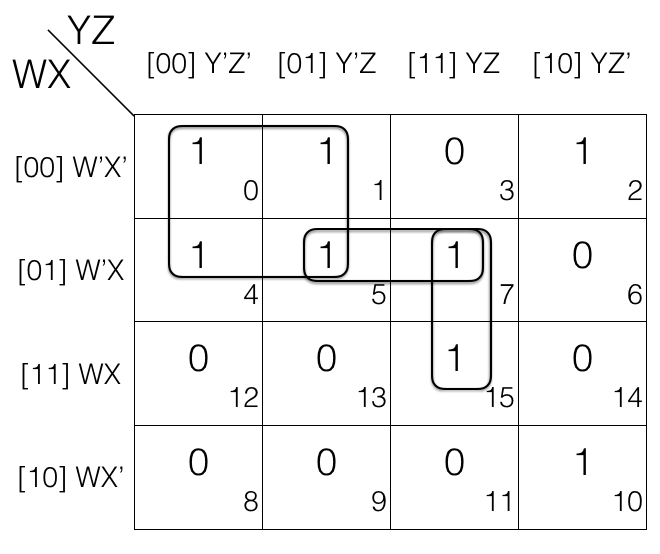
Now we will look for overlapping groups.

If we look at the K-map we will see that m7 in pair (m5, m7) and pair (m7, m15) is shared in both the groups. So both the pairs are overlapping groups.

Similarly m5 in pair (m5, m7) and quad (m0, m1, m4, m5) is shared in both the groups. So the pair and quad are overlapping groups.

And there is no other overlapping groups so, we will now check for redundant groups.

Looking at the K-map we can tell pair (m5, m7) is redundant as m5 is covered in quad (m0, m1, m4, m5) and m7 is covered in pair (m7, m15). So we will remove the pair (m5, m7).

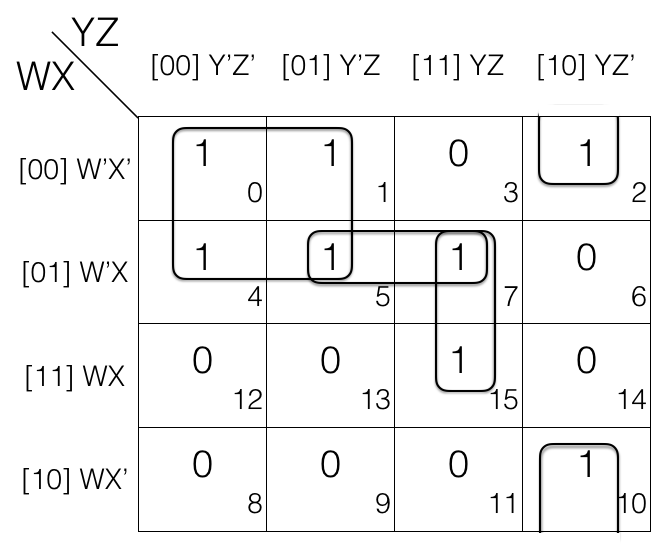
Now we will write down the marked groups and find the reduced expression.

Quad = (m0, m1, m4, m5) = (W’X’Y’Z’ + W’X’Y’Z) + (W’XY’Z’ + W’XY’Z)
= W’X’Y’ + W’XY’ [Z’ changed, so removed]
= W’Y’ [X’ changed to X, so removed]

1st pair = (m7, m15)
= W’XYZ + WXYZ
= XYZ [W’ changed to W, so removed]

2nd pair = (m2, m10)
= W’X’YZ’ + WX’YZ’
= X’YZ’ [W’ changed to W, so removed]

Now we OR (+) the results to get the final reduced expression.

F = W’Y’ + XYZ + X’YZ’

This is the required answer.

POS form reduction using K-map

Reduction rules for POS using K-map

There are a couple of rules that we use to reduce POS using K-map. First we will cover the rules step by step then we will solve problem. So lets start...

Pair reduction Rule

Consider the following 4 variables K-map.

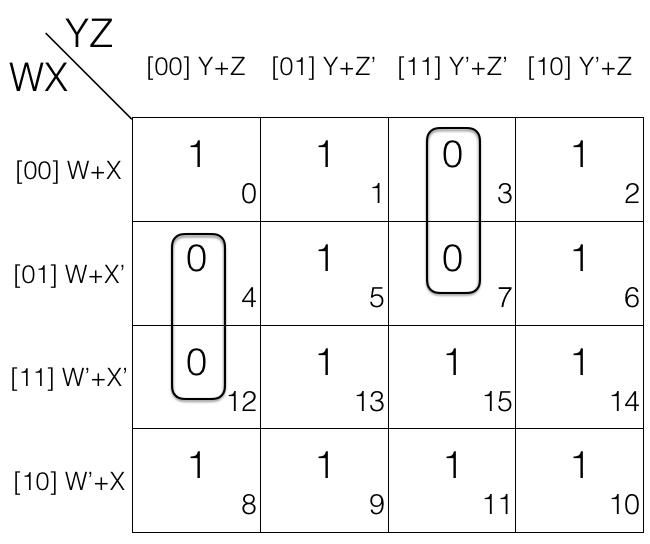
Now we mark the cells in pair (set of 2) having value 0.

1st pair = (W+X’+Y+Z) . (W’+X’+Y+Z)
2nd pair = (W+X+Y’+Z’) . (W+X’+Y’+Z’)
(the pairs are in Product of Sums POS form)

Now we will remove the variable that changed in the 1st and 2nd pair. Looking at the 1st pair W changed to W’ so we remove it. Looking at the 2nd pair X changed to X’ so we remove it.

So the updated pairs after reduction are given below.

1st pair
= (W+X’+Y+Z) . (W’+X’+Y+Z)
= (X’+Y+Z)

2nd pair
= (W+X+Y’+Z’) . (W+X’+Y’+Z’)
= (W+Y’+Z’)

Note! pair reduction rule removes 1 variable.

Quad reduction Rule

Consider the following 4 variables K-map.

Mark the cells in quad (set of 4) having value 0.

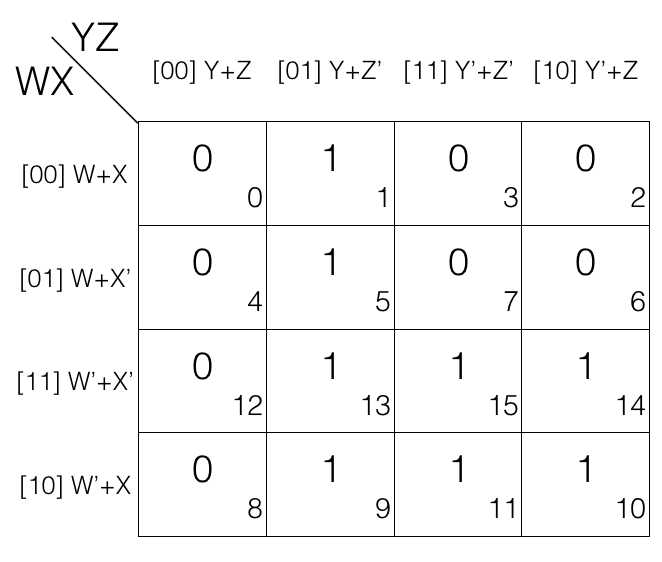
1st quad = (W+X+Y+Z) . (W+X’+Y+Z) . (W’+X’+Y+Z) . (W’+X+Y+Z)
2nd quad = (W+X+Y’+Z’) . (W+X+Y’+Z) . (W+X’+Y’+Z’) . (W+X’+Y’+Z)
(the quads are in Product of Sums POS form)

Now we will remove the variable that changed in the 1st and 2nd quad. Looking at the 1st quad W’ and X’ changed to W and X so, we remove them and looking at the 2nd quad X’ and Z changed to X and Z’ so, we remove them.

So the updated quads after reduction

1st quad
= [(W+X+Y+Z) . (W+X’+Y+Z)] . [(W’+X’+Y+Z) . (W’+X+Y+Z)]
= (W+Y+Z) . (W’+Y+Z)
= (Y+Z)

2nd quad
= [(W+X+Y’+Z’) . (W+X+Y’+Z)] . [(W+X’+Y’+Z’) . (W+X’+Y’+Z)]
= (W+X+Y’) . (W+X’+Y’)
= (W+Y’)

Note! quad reduction rule removes 2 variables.

Octet reduction Rule

Consider the following 4 variables K-map.

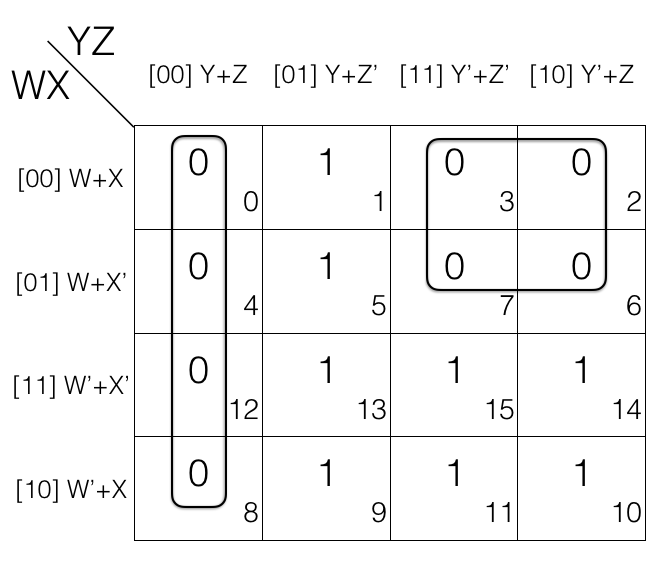
Mark the cells in octet (set of 8) having value 0.

Octet
= (W+X+Y+Z) . (W+X+Y+Z’) . (W+X+Y’+Z’) . (W+X+Y’+Z)
. (W+X’+Y+Z) . (W+X’+Y+Z’) . (W+X’+Y’+Z’) . (W+X’+Y’+Z)

(the octet is in Product of Sums POS form)

Now we will remove the variable that changed in the octet. Looking at the octet moving top to bottom: X’ changed to X, moving from left to right: Y’ changed to Y and moving from left to right: Z’ changed to Z.

Updated octet after reduction

octet
= [(W+X+Y+Z) . (W+X+Y+Z’)]
. [(W+X+Y’+Z’) . (W+X+Y’+Z)]
. [(W+X’+Y+Z) . (W+X’+Y+Z’)]
. [(W+X’+Y’+Z’) . (W+X’+Y’+Z)]

= [(W+X+Y) . (W+X+Y’)]
. [(W+X’+Y) . (W+X’+Y’)]

= (W+X) . (W+X’)
= W

Note! octet reduction rule will remove 3 variables.

Map Rolling reduction Rule

In this we consider that the K-map top edge is connected with the bottom edge and left edge is connected with the right edge then we mark the pairs, quads and octets. Lets check few examples.

Map Rolling reduction Rule - marking the pairs

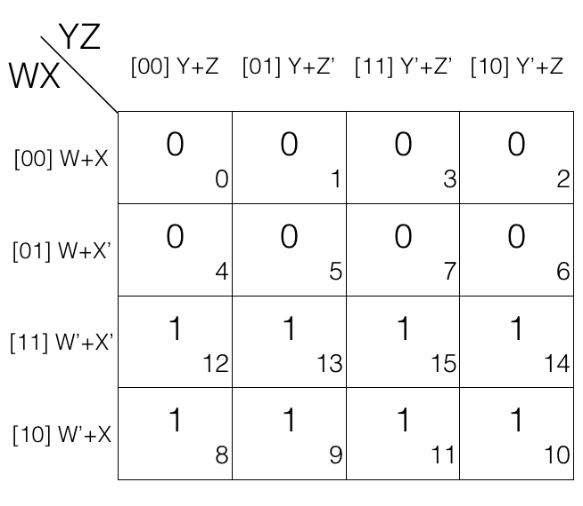
Consider the following 4 variables K-map.

1st pair = (W+X+Y+Z’) . (W’+X+Y+Z’)

2nd pair = (W’+X’+Y+Z) . (W’+X’+Y’+Z)

in 1st pair W change to W’
in 2nd pair Y change to Y’

so we will remove them.

Updated pairs after reduction

1st pair
= (W+X+Y+Z’) . (W’+X+Y+Z’)
= (X+Y+Z’)

2nd pair
= (W’+X’+Y+Z) . (W’+X’+Y’+Z)
= (W’+X’+Z)

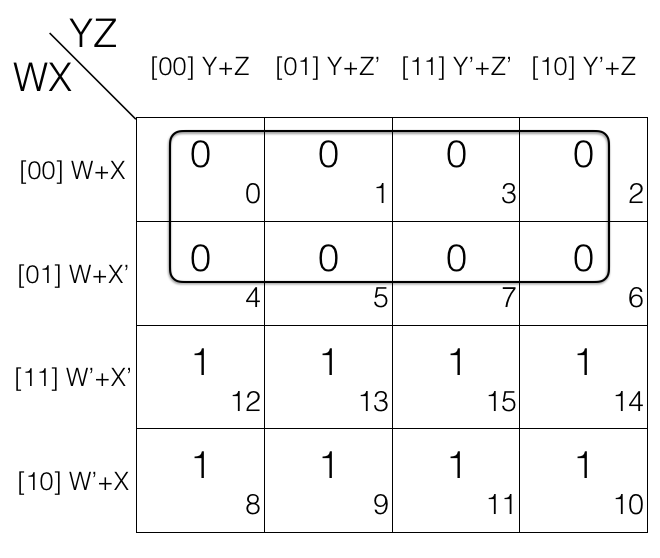
Map Rolling reduction Rule - marking the quads

Consider the following 4 variables K-map.

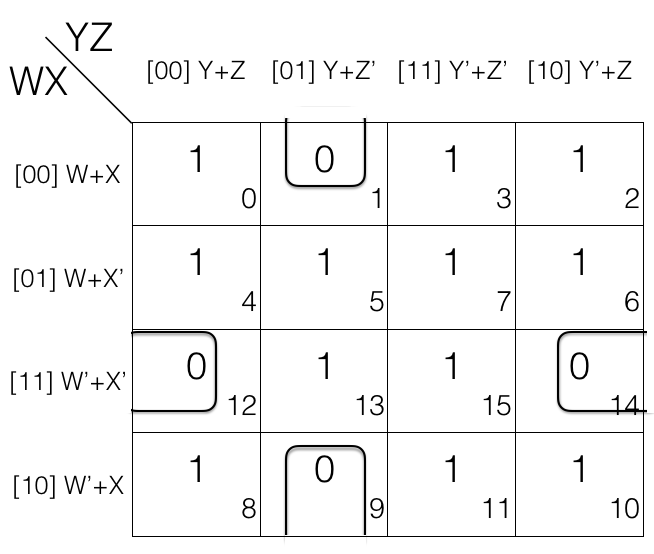
1st quad
= (W+X+Y+Z’) . (W+X+Y’+Z’) . (W’+X+Y+Z’) . (W’+X+Y’+Z’)

2nd quad
= (W+X’+Y+Z) . (W’+X’+Y+Z) . (W+X’+Y’+Z) . (W’+X’+Y’+Z)

In 1st quad and 2nd quad W’ change to W and Y’ changes to Y so we will remove them.

Updated quads after reduction

1st quad
= [(W+X+Y+Z’) . (W+X+Y’+Z’)] . [(W’+X+Y+Z’) . (W’+X+Y’+Z’)]
= (W+X+Z’) . (W’+X+Z’)
= (X+Z’)

2nd quad
= [(W+X’+Y+Z) . (W’+X’+Y+Z)] . [(W+X’+Y’+Z) . (W’+X’+Y’+Z)]
= (X’+Y+Z) . (X’+Y’+Z)
= (X+Z)

Map Rolling reduction Rule - marking the octets

Consider the following 4 variables K-map.

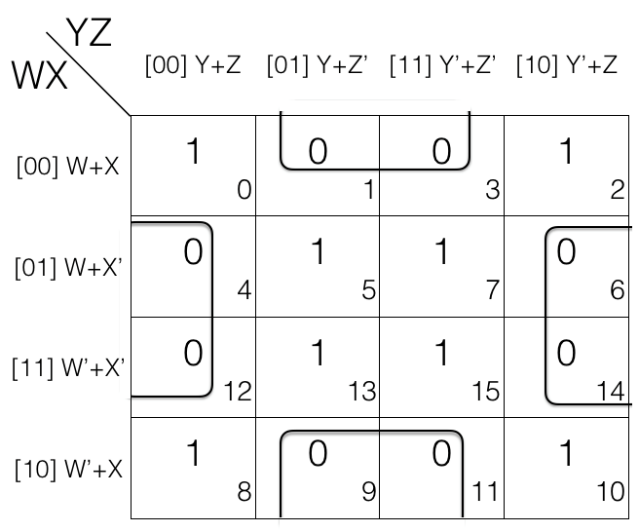
Octet
= (W+X+Y+Z) . (W+X+Y+Z’)
. (W+X+Y’+Z’) . (W+X+Y’+Z)
. (W’+X+Y+Z) . (W’+X+Y+Z’)
. (W’+X+Y’+Z’) . (W’+X+Y’+Z)

Looking at the octet we can tell that W’ changed to W, Y’ changed to Y and Z’ changed to Z so we will remove them.

Octet
= [(W+X+Y+Z) . (W+X+Y+Z’)]
. [(W+X+Y’+Z’) . (W+X+Y’+Z)]
. [(W’+X+Y+Z) . (W’+X+Y+Z’)]
. [(W’+X+Y’+Z’) . (W’+X+Y’+Z)]

= [(W+X+Y) . (W+X+Y’)]
. [(W’+X+Y) . (W’+X+Y’)]
= (W+X) . (W’+X)
= X

Overlapping Groups

When a value in a cell of K-map is encircled in more that one group (pair, quad or octet) then we call such groups an overlapping groups. Lets check an example...

Overlapping Groups - marking the overlapping groups

Consider the following 4 variables K-map.

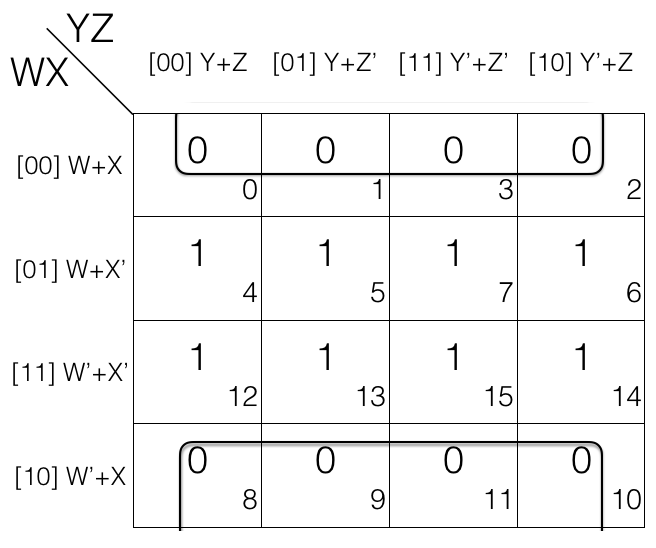
1st pair = (W+X’+Y+Z) . (W+X’+Y+Z’)
= M4 . M5

2nd pair = (W’+X’+Y’+Z’) . (W’+X’+Y’+Z)
= M15 . M14

quad = [(W+X’+Y+Z’) . (W+X’+Y’+Z’)]
. [(W’+X’+Y+Z’) . (W’+X’+Y’+Z’)]
= M5 . M7 . M13 . M15

If we look at M5 and M15 they are overlapping.

Overlapping groups helps in getting simpler expression after reduction.

1st pair = (W+X’+Y+Z) . (W+X’+Y+Z’)
= (W+X’+Y)

2nd pair = (W’+X’+Y’+Z’) . (W’+X’+Y’+Z)
= (W’+X’+Y’)

quad = [(W+X’+Y+Z’) . (W+X’+Y’+Z’)]
. [(W’+X’+Y+Z’) . (W’+X’+Y’+Z’)]
= (W+X’+Z’) . (W’+X’+Z’)
= X’+Z’

Redundant Groups

After marking out the overlapping groups it is important to also check for redundant groups. If all the values of a group G (pair, quad or octet) is covered (overlapping) with other groups then that group G is redundant and ignored. Lets check an example.

Finding the redundant groups

Consider the following 4 variables K-map.

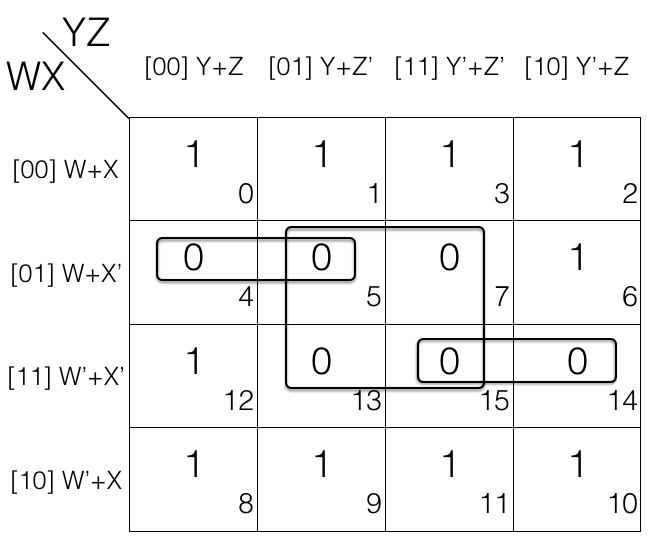
1st pair = M5 . M7

2nd pair = M12 . M13

3rd pair = M5 . M13

If we look at M5 and M13 i.e. 3rd pair, it is a redundant group as M5 and M13 is covered in 1st and 2nd pair so we will remove the redundant group (3rd pair).

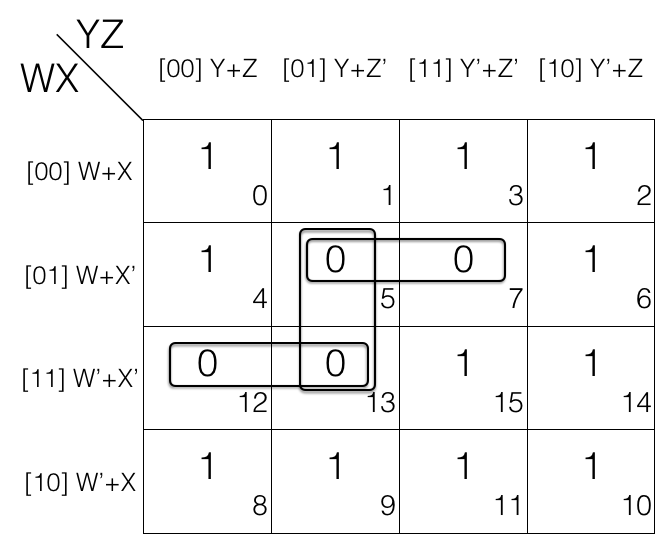
Updated pairs after reduction

1st pair = M5 . M7
= (W+X’+Y+Z’) . (W+X’+Y’+Z’)
= (W+X’+Z’)

2nd pair = M12 . M13
= (W’+X’+Y+Z) . (W’+X’+Y+Z’)
= (W’+X’+Y)

Summary of Reduction rules for POS using K-map

1. Prepare the truth table for the function
2. Draw an empty K-map (2-variables, 3-variables, so on)
3. Fill the cells with value 0 for which the output is 0
4. Fill rest of the cells with value 1
5. Mark the Octets, Quads and Pairs by encircling the value 0s
(also check map rolling, overlapping groups and remove redundant groups)
6. AND (.) the reduced expression to get the final answer

Time to solve problem :-)

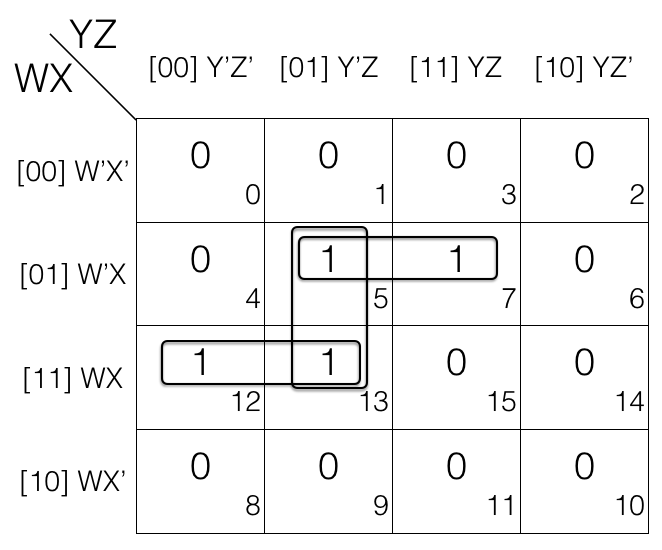
POS reduction using K-map

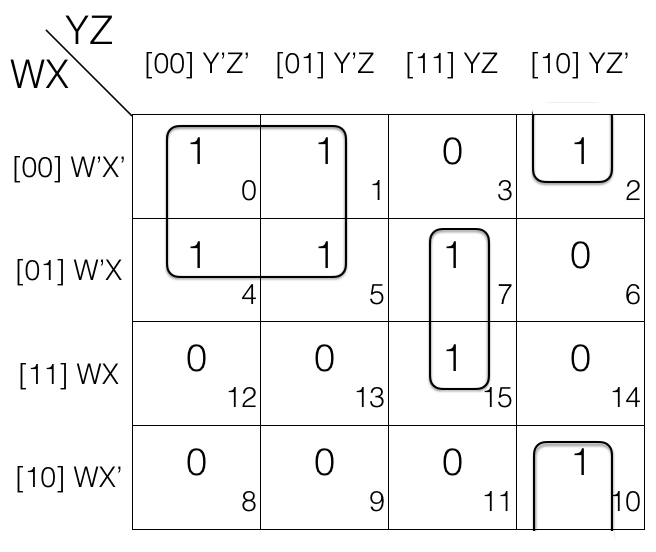
Reduce F(A,B,C,D) = ∏(0,1,2,4,5,7,10,15) using K-map. Since function F has 4 variables so we will create a 4 variable K-map having 24 = 16 cells.

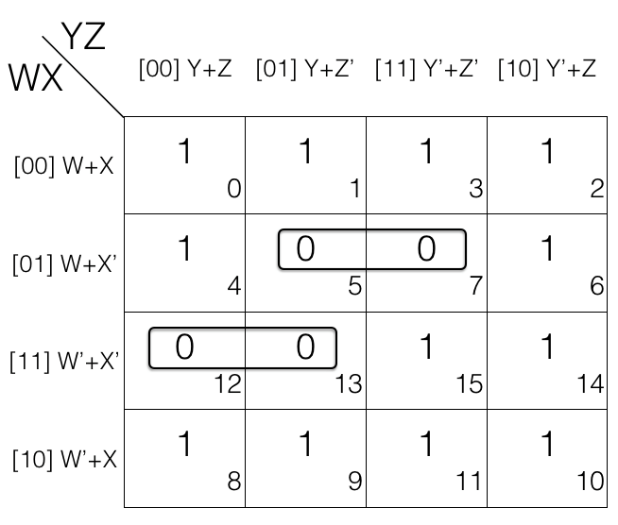
Now fill the cell marked with subscript 0,1,2,4,5,7,10 and 15 with value 0 as we are dealing with Product of Sums POS. And fill rest of the cells with value 1.

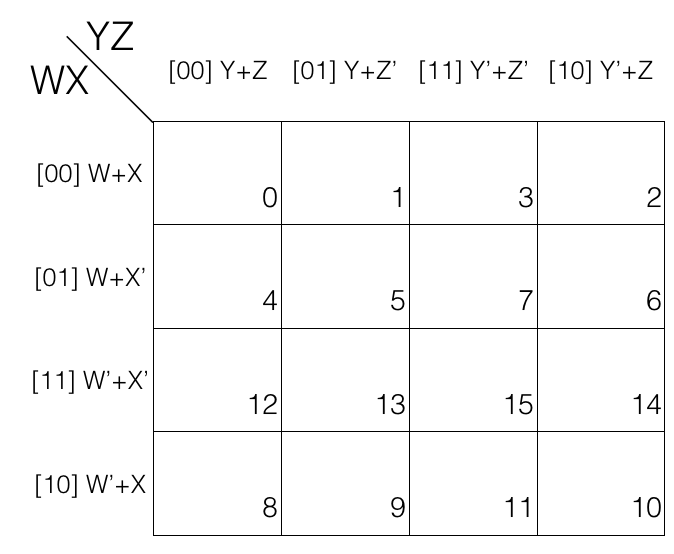
Now we will mark the octets, quads and pairs.

Looking at the K-map we can tell that there is no octets so we will look for quads.

Looking for quads and marking them.

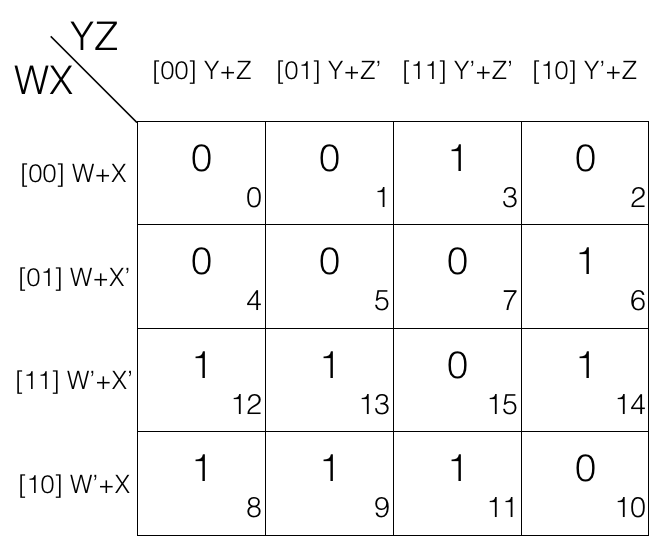
No more quad left so we will now look for pairs and mark them.

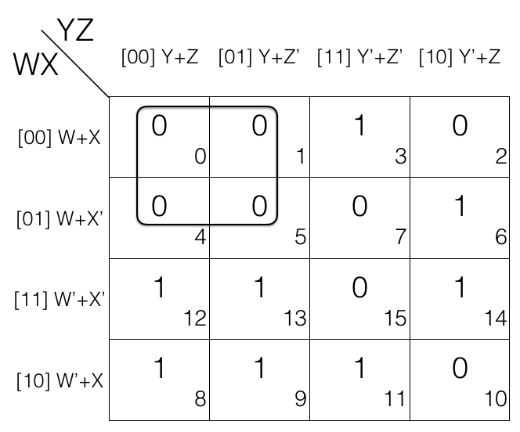
No more pairs left so we will move to map rolling and look for octet, quad and pair.

There is no octet and quad but on map rolling we do find a pair. So marking the pair.

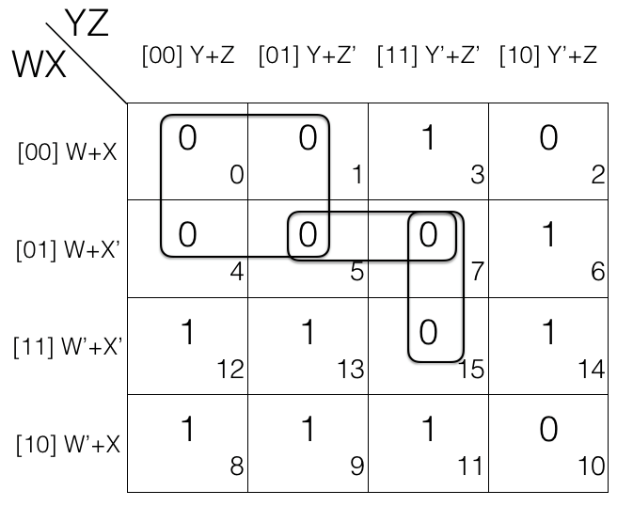
Now looking for overlapping groups.

If we look at the K-map we will see that M7 in pair (M5,M7) and pair (M7, M15) is shared in both the groups so both the pairs are overlapping groups.

Similarly M5 in pair (M5,M7) and quad (M0, M1, M4, M5) is shared in both the groups so the pair and quad are overlapping groups.

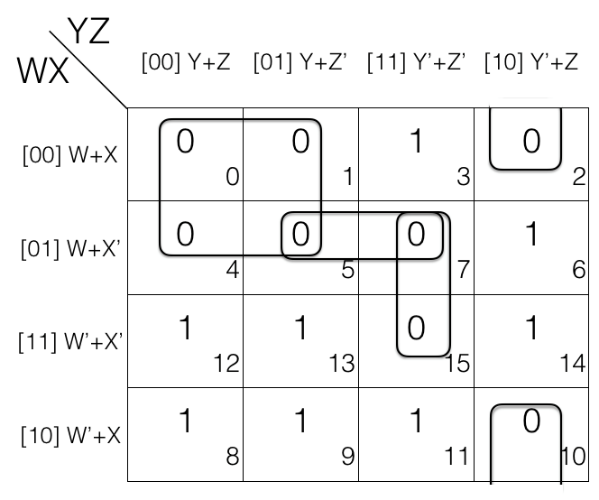
And there is no other overlapping groups so we will now check for redundant groups.

Check for redundant groups.

Looking at the K-map we can tell pair (M5,M7) is redundant as M5 is covered in quad (M0, M1, M4, M5) and M7 is covered in pair (M7, M15) so we will remove the pair (M5,M7).

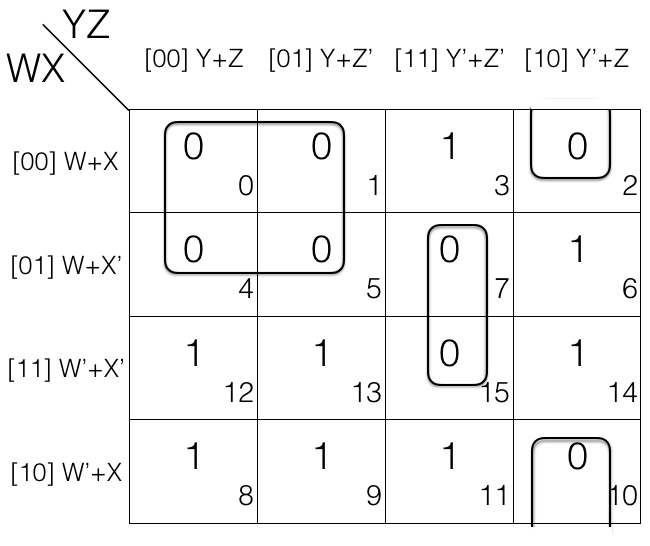
Now we will write down the marked groups and find the reduced expression.

Quad = M0 . M1 . M4 . M5
= [(W+X+Y+Z) . (W+X+Y+Z’)]
. [(W+X’+Y+Z) . (W+X’+Y+Z’)]
= (W+X+Y) . (W+X’+Y)      [Z’ changed, so removed]
= (W+Y)      [X’ changed, so removed]

1st pair = M7 . M15
= [(W+X’+Y’+Z’) . (W’+X’+Y’+Z’)]
= (X’+Y’+Z’)      [W’ changed to W, so removed]

2nd pair = M2 . M10
= [(W+X+Y’+Z) . (W’+X+Y’+Z)]
= (X+Y’+Z)      [W’ changed to W, so removed]

Now we AND (.) the results to get the final reduced expression.

F = (W+Y) . (X’+Y’+Z’) . (X+Y’+Z)

This is the required answer.

1.5 Design of combinational circuits using Boolean expression and K-map

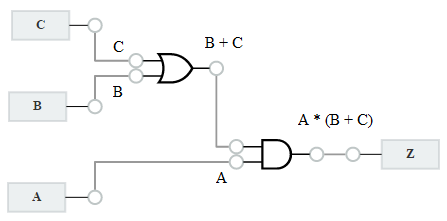
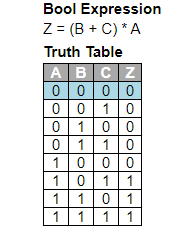
To obtain the boolean expressions and truth tables from the combinational logic circuit, we need to analyse the circuit. First ensure that the circuit is combinational - that is there is no feedback of an output to an input that the output depends on.

Boolean Expressions

1. Label all inputs -- input variables
2. Label all outputs -- output functions
3. Label all intermediate signals (outputs that feed inputs)

For each output functions, write it in terms of its input variables and intermediate signals, and then expand intermediate signals until the outputs are expressed only in terms of the inputs.

Truth tables

The truth table can be derived from the Boolean expressions, or by directly working out from the circuit, the outputs for each possible combination of inputs.

If there are n input variables

• There are 2n possible binary input combinations
• There are 2n entries in the truth table for each output

From the examples below, change the inputs to observe the outputs.

Example Circuits

Karnaugh introduced a method for simplification of Boolean functions in an easy way. This method is known as Karnaugh map method or K-map method. It is a graphical method, which consists of 2n cells for ‘n’ variables. The adjacent cells are differed only in single bit position.

K-Maps for 2 to 5 Variables

K-Map method is most suitable for minimizing Boolean functions of 2 variables to 5 variables. Now, let us discuss about the K-Maps for 2 to 5 variables one by one.

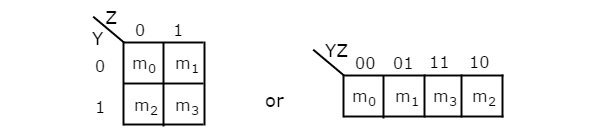
2 Variable K-Map

The number of cells in 2 variable K-map is four, since the number of variables is two. The following figure shows 2 variable K-Map.

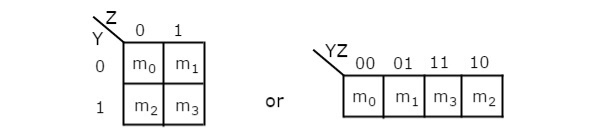
• There is only one possibility of grouping 4 adjacent min terms.
• The possible combinations of grouping 2 adjacent min terms are {(m0, m1), (m2, m3), (m0, m2) and (m1, m3)}.

3 Variable K-Map

The number of cells in 3 variable K-map is eight, since the number of variables is three. The following figure shows 3 variable K-Map.

• There is only one possibility of grouping 8 adjacent min terms.
• The possible combinations of grouping 4 adjacent min terms are {(m0, m1, m3, m2), (m4, m5, m7, m6), (m0, m1, m4, m5), (m1, m3, m5, m7), (m3, m2, m7, m6) and (m2, m0, m6, m4)}.
• The possible combinations of grouping 2 adjacent min terms are {(m0, m1), (m1, m3), (m3, m2), (m2, m0), (m4, m5), (m5, m7), (m7, m6), (m6, m4), (m0, m4), (m1, m5), (m3, m7) and (m2, m6)}.
• If x=0, then 3 variable K-map becomes 2 variable K-map.

4 Variable K-Map

The number of cells in 4 variable K-map is sixteen, since the number of variables is four. The following figure shows 4 variable K-Map.

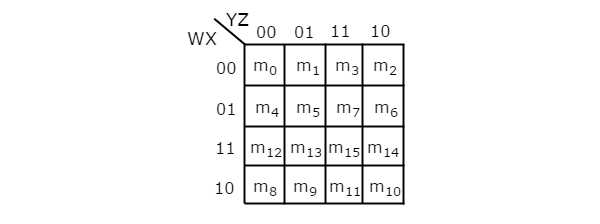
• There is only one possibility of grouping 16 adjacent min terms.
• Let R1, R2, R3 and R4 represents the min terms of first row, second row, third row and fourth row respectively. Similarly, C1, C2, C3 and C4 represents the min terms of first column, second column, third column and fourth column respectively. The possible combinations of grouping 8 adjacent min terms are {(R1, R2), (R2, R3), (R3, R4), (R4, R1), (C1, C2), (C2, C3), (C3, C4), (C4, C1)}.
• If w=0, then 4 variable K-map becomes 3 variable K-map.

5 Variable K-Map

The number of cells in 5 variable K-map is thirty-two, since the number of variables is 5. The following figure shows 5 variable K-Map.

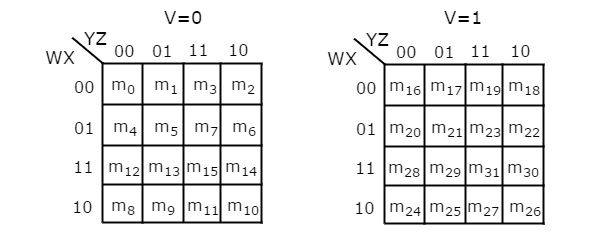
• There is only one possibility of grouping 32 adjacent min terms.
• There are two possibilities of grouping 16 adjacent min terms. i.e., grouping of min terms from m0 to m15 and m16 to m31.
• If v=0, then 5 variable K-map becomes 4 variable K-map.

In the above all K-maps, we used exclusively the min terms notation. Similarly, you can use exclusively the Max terms notation.

1.6 Encoder, decoder, half, and full adder.

ENCODER

• It is a combinational circuit that converts binary information in the form of a 2N input lines into N output lines, which represent N bit code for the input.
• For simple encoders, only one input line is active at a time.
• For example, Octal to Binary encoder takes 8 input lines and generates 3 output lines.

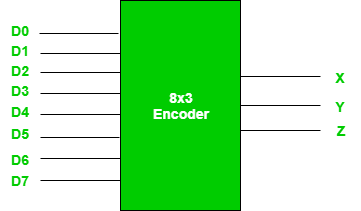
Fig: 8X3 Encoder (ref. 2)

Truth Table –

• From the above truth table it is seen that the output is 000 when D0 is active; 001 when D1 is active; 010 when D2 is active and so on.

Implementation –
 

• From the above truth table, the output Z is active when the input octal digit is 1, 3, 5, or 7.
• Y is active when input octal digit is 2, 3, 6, or 7 and X is active when input octal digits 4, 5, 6, or 7.
• Hence, the Boolean functions would be:

X = D4 + D5 + D6 + D7

Y = D2 +D3 + D6 + D7

Z = D1 + D3 + D5 + D7

• Hence, the encoder is realized with OR gates as follows:

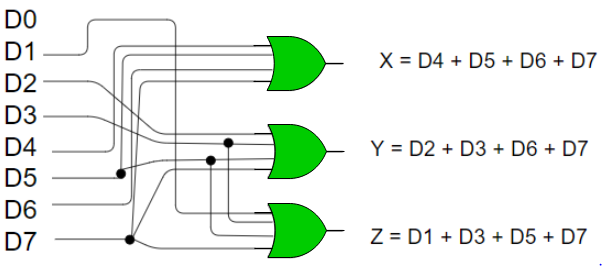
Fig: 12 8:3 encoder (ref.2)

• The limitation of the encoder is that only one input is active at a time.
• If more than one input is active, then the output of the encoder is undefined.
• For example, if D6 and D3 are both active, then, our output would be 111 which is the output for D7.
• The problem arises when all inputs are 0.
• The encoder gives output 000 which is the output for D0. To avoid this, an extra bit is added to the output which is called the valid bit whose value is 0 when all inputs are 0 or 1.

Key Takeaways:

1. It is a combinational circuit that converts binary information in the form of a 2N input lines into N output lines, which represent N bit code for the input.
2. For simple encoders, only one input line is active at a time.

DECODER

• It works as an inverse of an encoder.
• It is a combinational circuit that converts n input lines into 2n output lines.
• Taking an example of a 3-to-8 line decoder.

Truth Table –

Implementation

D0 is high when X = 0, Y = 0 and Z = 0. Hence,

D0 = X’ Y’ Z’

Similarly,

D1 = X’ Y’ Z

D2 = X’ Y Z’

D3 = X’ Y Z

D4 = X Y’ Z’

D5 = X Y’ Z

D6 = X Y Z’

D7 = X Y Z

Hence,

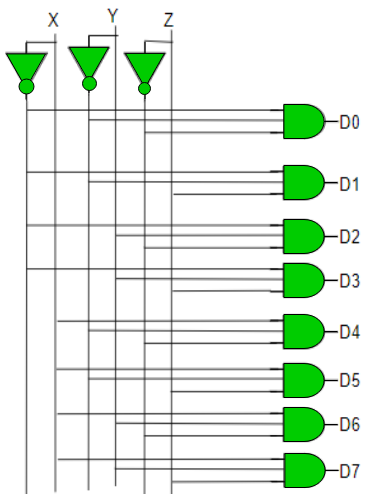
Fig: Decoder (ref.2)

Key Takeaways:

1. It works as an inverse of an encoder.
2. It is a combinational circuit that converts n input lines into 2n output lines.

HALF ADDER

      It is a combinational circuit which has two inputs and two outputs.

      It is designed to add two single bit binary number A and B.

      It has two outputs carry and sum.

Block diagram

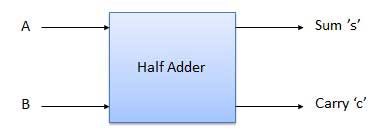
Fig: Half adder (ref. 2)

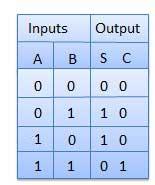
Truth Table

Circuit Diagram

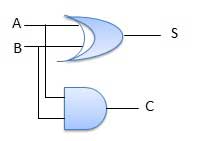
Fig: Half adder (ref. 2)

FULL ADDER

      It is developed to overcome the drawback of the Half Adder circuit.

      It can add two one-bit numbers A and B and a carry C.

      It is a three-input and two output combinational circuit.

Block diagram

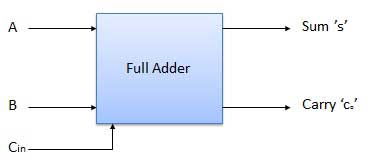
Fig: Full adder (ref. 2)

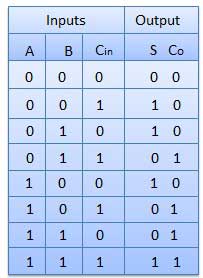
Truth Table

Circuit Diagram

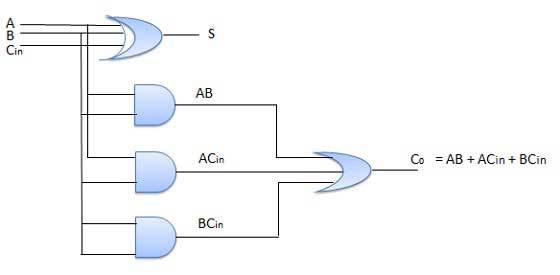
Fig: Full adder (ref. 2)

Key Takeaways:

1. Half adder is a combinational circuit that has two inputs and two outputs.
2. Since there is no provision for carrying in the half adder, the full adder is developed to overcome the drawback.

Reference Books:

[R1] Tokheim, “Digital Electronics-Principles and Application”, 6th edition, Tata McGraw Hill, New Delhi.

[R2] A Jaico and Charles H. Roth, “Fundamentals of Logic Design” Jr. Forth Edition.

[R3] K. R. Botkar, “Integrated Circuits”, Khanna Publication, New Delhi.

[R4] James, “Operational Amplifier and Linear Integrated Circuits Theory and Application.”

[R5] P John Paul, “Electronics Devices and Circuits”, New Age International Publications.

[R6] P. S. Bimbhra, “Power Electronics”, Khanna Publications.

[R7] NPTEL course on Digital Electronics Circuit, IIT, Kharagpur.

Https://nptel.ac.in/courses/108105132/

[R8] NPTEL course on Integrated circuit, MOSFET, OPAMP, and their applications IISC Banglore. Https://nptel.ac.in/courses/108/108/108108111/

[R9] NPTEL course on power electronics by IIT Kharagpur.

Https://nptel.ac.in/courses/108/105/108105066/