Unit – 2
Laplace Transform
Let f(t) be any function of t defined for all positive values of t. Then the Laplace transform of the function f(t) is defined as-
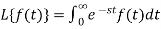
Provided that the integral exists, here ‘s’ is the parameter which could be real or complex.
The inverse of the Laplace transform can be defined as below-
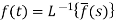
Here 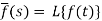
f(t) is called the inverse Laplace transform of 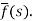
L is called the Laplace transformation operator.
Conditions for the existence of Laplace transforms-
The Laplace transform of f(t) exists for s>a, if
1. f(t) is a continuous function.
2. 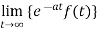 is finite.
is finite.
Important formulae-
1. 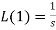
2. 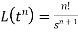
3. 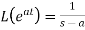
4. 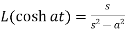
5. 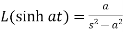
6. 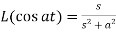
7. 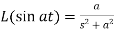
Example-1: Find the Laplace transform of the following functions-
1. 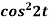 2.
2. 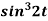
Sol. 1.
Here 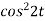
So that we can write it as-
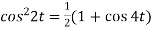
Now-
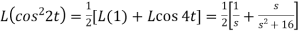
2. Since 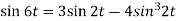
Or 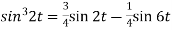
Now-
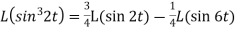
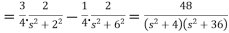
Example-2: Find the Laplace transform of (1 + cos 2t)
Sol. 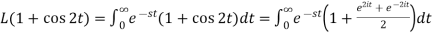
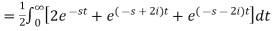
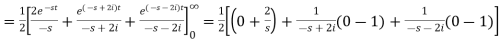
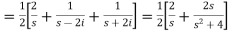
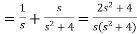
So that-
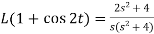
Inverse Laplace transforms-
The inverse of the Laplace transform can be defined as below-
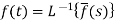
Here 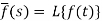
f(t) is called the inverse Laplace transform of 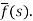
L is called the Laplace transformation operator.
Important formulae-
1. 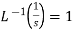 2.
2. 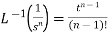
3. 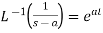 4.
4. 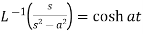
5. 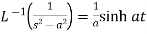 6.
6. 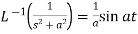
7. 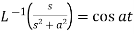 8.
8. 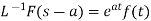
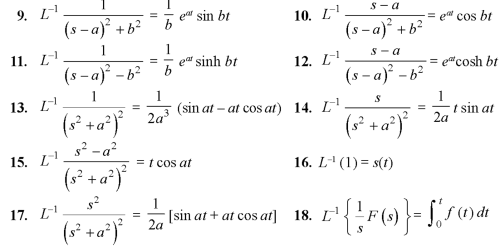
1. Linearity property-
Let a and b be any two constants and 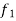 ,
, 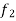 any two functions of t, then-
any two functions of t, then-
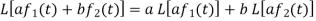
Proof: 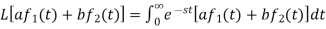
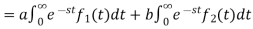
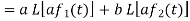
Hence proved.
2. First shifting property (Theorem)- If 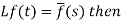
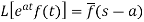
Proof: By definition-
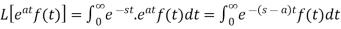
Let (s – a) = r
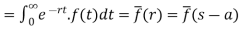
Hence proved.
We can find the following results with the help of the above theorem-
1. 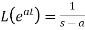
2. 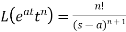
4. 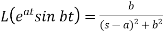
5. 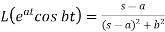
6. 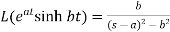
7. 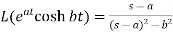
Here s>a in each case.
Example-1: Find the Laplace transform of t sin at.
Sol. Here-
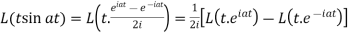
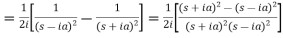
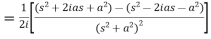
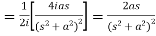
Example-2: Find the Laplace transform of 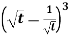
Sol. Here-
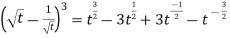
So that-
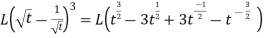
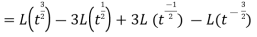
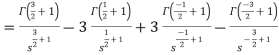
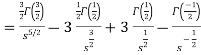
As we know that- 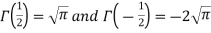
So that-
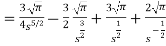
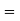
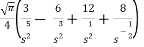
Hence-
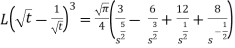
Example-3: Find the Laplace transform of the following function-
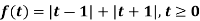
Sol. The given function f(t) can be written as-
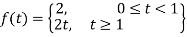
So that, by definition,
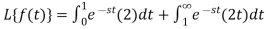
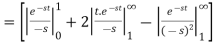
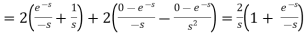
1. 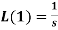
Proof: by the definition of Laplace transform-
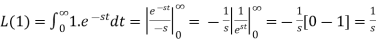
So that-
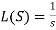
2. 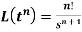
Proof: by the definition of Laplace transform-
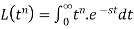
Let 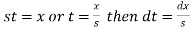
So that-
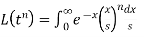
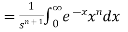
We know that-
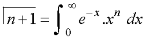
Then-
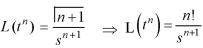
3. 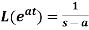
Proof: by the definition of Laplace transform-
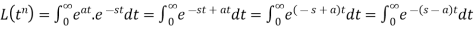
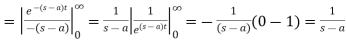
4. 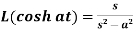
Proof: here we know that,
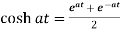
So that-
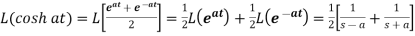
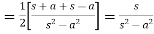
5. 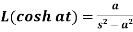
Proof: here we know that,
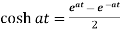
So that-
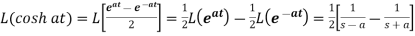
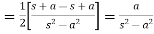
6. 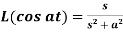
Proof: here we know that,
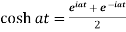
So that-
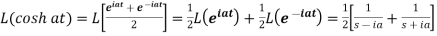
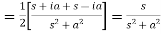
7. 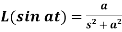
Proof: here we know that,
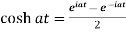
So that-
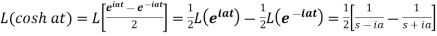
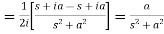
1. Transforms of periodic functions-
If f(t) is a periodic function with f(t + T) = f(t), then-
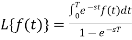
2. Transforms of Bessel functions 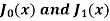 -
-
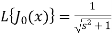
Since,
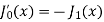
So that-
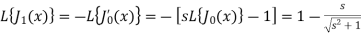
3. Transforms of Laguerre’s functions 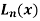 -
-
We know that-
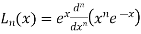
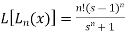
4. Transforms of error functions-
We know that-
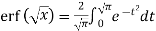
So that it Laplace transform will be-
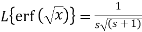
Example-1: Find the Laplace transform of the following function (Half-wave rectifier)-
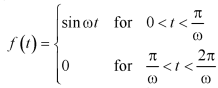
Sol. By the definition-
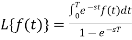
f(t) is a periodic function and 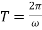
So that-
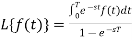
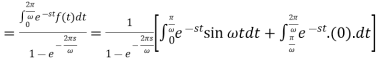
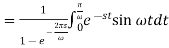
As we know that-
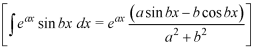
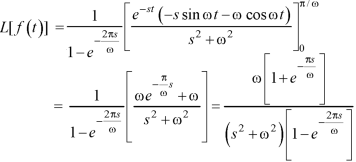
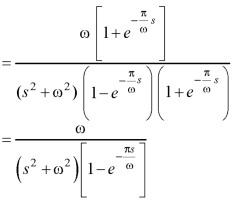
Example-2: Find the Laplace transform of the periodic function-
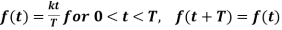
Sol. By the definition-
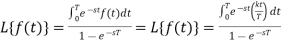
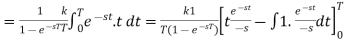
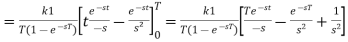
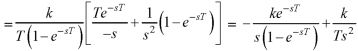
Example-3: Evaluate the following-
1. 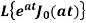
2. 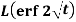
Sol. 1.
As we know that-
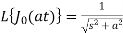
Now, by shifting property-
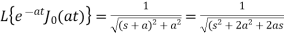
2.
We know that-
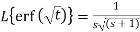
So that-
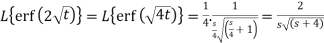
Laplace transform of the derivative of f(t)-
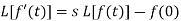
Here 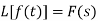
Proof: by the definition of Laplace transform-
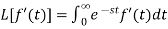
On integrating by parts, we get-
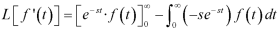
Since 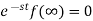
Then-
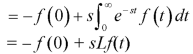
So that-
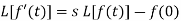
Laplace transform of integral of f(t) -
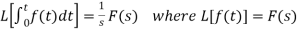
Proof: Suppose
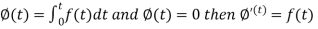
We know that-
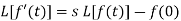
So that-
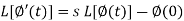
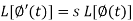
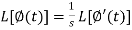
Putting the values of 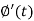 and
and 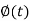 , we get-
, we get-
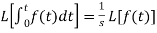
Laplace transform of the function 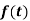 multiplied by t
multiplied by t
If 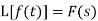 , then-
, then-
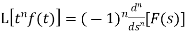
Proof: 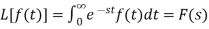
Differentiate w.r.t. x, we get-
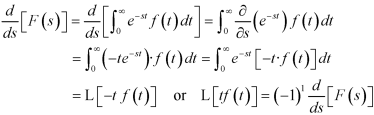
Similarly-
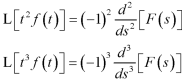
And
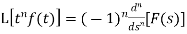
Example-4: Find the Laplace transform of 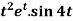 .
.
Sol. Here-
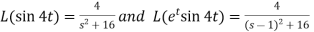
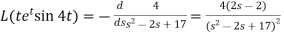
Now-
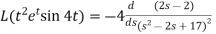
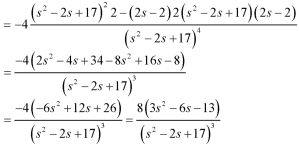
The unit step function u(t – a) is defined as-
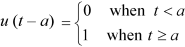
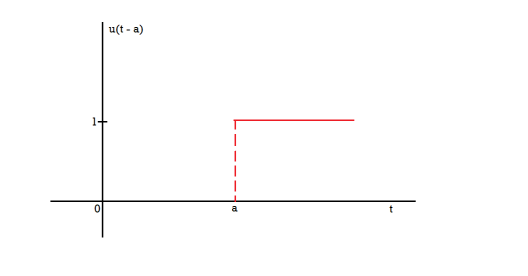
Laplace transform of unit functions-
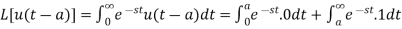
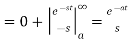
Example-1: Express the function given below in terms of unit step function and find its Laplace transform as well-
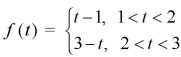
Sol. Here we are given-
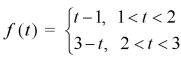
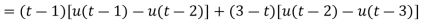
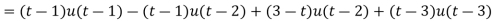
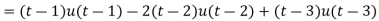
So that-
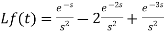
Example-2: Find the Laplace transform of the following function by using unit step function-
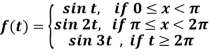
Sol. 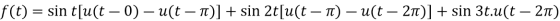
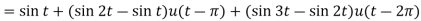
Since 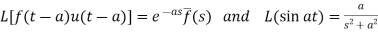
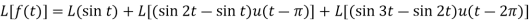
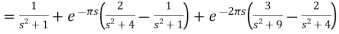
Second shifting theorem-
If 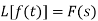
Then,
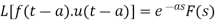
Proof: 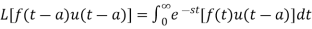
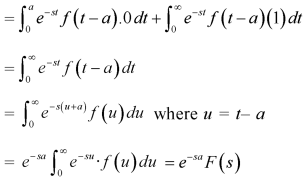
Example-3: Find the Laplace transform of 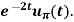
Where-
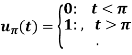
Sol. Here we are given—
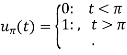
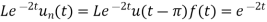
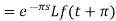
As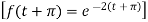
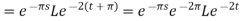
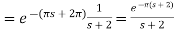
Impulse- When a large force acts for a short time, then the product of the force and the time is called impulse.
The unit impulse function is the limiting function.
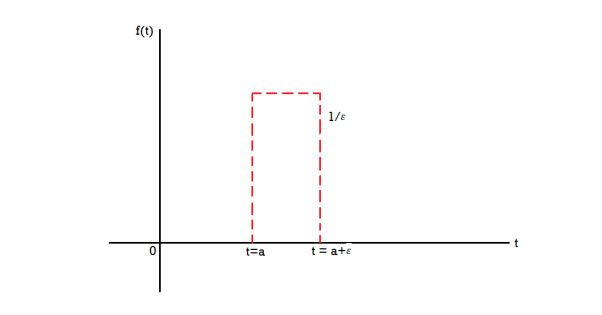
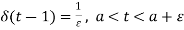
= 0, otherwise
The unit impulse function can be defined as-
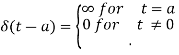
And
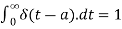
Laplace transform of unit impulse function-
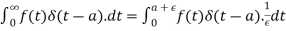
We know that-
Mean value theorem- 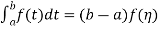
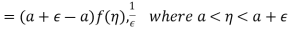
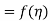
As 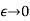 , then we get-
, then we get- 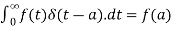
When 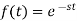 then we have
then we have 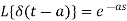
Example-1: Evaluate-
1. 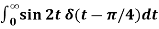
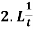
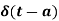
Sol.1. As we know that- 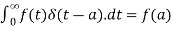
So that-
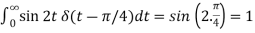
2. As we know that-
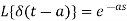
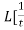
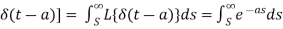
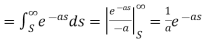
Example-2: 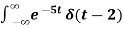
Sol. 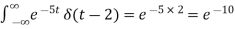
Step by step procedure to solve a linear differential equation by using Laplace transform-
1. Take Laplace transform of both sides of the given differential equation.
2. Transpose the terms with negative sign to the right.
3. Divide by the coefficient of 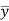 , getting
, getting 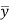 as a known function of s.
as a known function of s.
4. Resolve the function of s into partial fractions and take the inverse transform of both sides.
We will get y as a function of t. Which is the required solution.
Example-1: Use Laplace transform method to solve the following equation-
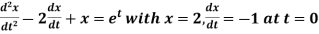
Sol. Here we have-
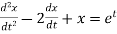
Take Laplace transform of both sides, we get-
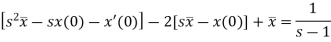
It becomes-
(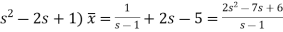
So that-
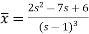
Now breaking it into partial fractions-
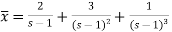
We get the following results on inversion-
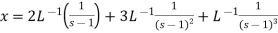
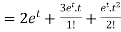
Example-2: Use Laplace transform method to solve the following equation-
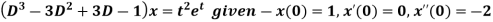
Sol.
Here, taking the Laplace transform of both sides, we get
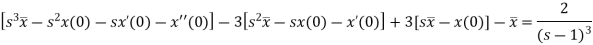
It becomes-
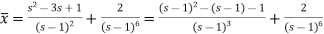
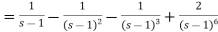
On inversion, we get-
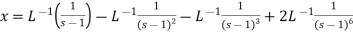
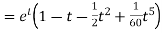
Example-3: Use Laplace transform method to solve the following equation-
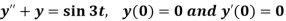
Sol. Here we have-
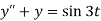
Taking Laplace transform of both sides, we get-
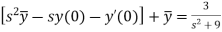
We get on putting given values-
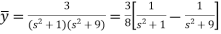
On inversion, we get-
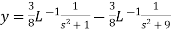
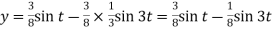
Example-4: Find the solution of the initial value problem by using Laplace transform-
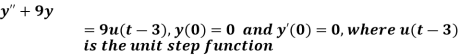
Sol. Here we have-
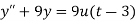
Taking Laplace transform, we get-
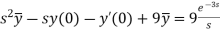
Putting the given values, we get-
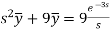
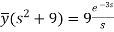
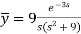
On inversion, we get-
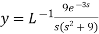
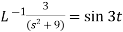
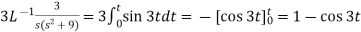 4
4
Now-
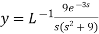
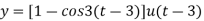
Reference Books
1. Erwin Kreyszig, “Advanced Engineering Mathematics”, Wiley India,10th Edition.
2. M.D. Greenberg, “Advanced Engineering Mathematics”, Pearson Education, 2 nd Edition.
3. Peter. V and O‟Neil, “Advanced Engineering Mathematics”, Cengage Learning,7th Edition.
4. S.L. Ross, “Differential Equations”, Wiley India, 3rd Edition.
5. S. C. Chapra and R. P. Canale, “Numerical Methods for Engineers”, McGraw-Hill, 7th Edition.
6. J. W. Brown and R. V. Churchill, “Complex Variables and Applications”, McGraw-Hill Inc, 8th Edition.