Unit – 6
Complex Variables
In the narrow sense of the term, the theory of function of a complex variable is the theory of analytic functions (cf. Analytic function) of one or several complex variables. As an independent discipline, the theory of functions of a complex variable took shape in about the middle of the 19th century as the theory of analytic functions.
Complex function-
x + iy is a complex variable which is denoted by z
If for each value of the complex variable z = x + iy in a region R, we have one or more than one values of w = u + iv, then w is called a complex function of z.
And it is denoted as-
w = u(x , y) + iv(x , y) = f(z)
Neighbourhood of 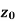
Let a point 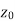 in the complex plane and z be any positive number, then the set of points z such that-
in the complex plane and z be any positive number, then the set of points z such that-
|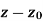 |<ε
|<ε
Is called ε- neighbourhood of 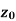
Limit of a function of a complex variable-
Suppose f(z) is a single valued function defined at all points in some neighbourhood of point 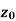 -
-
The-
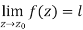
Example-1: Find-
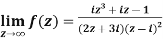
Sol. Here we have-
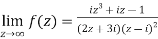
Divide numerator and denominator by 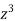 , we get-
, we get-
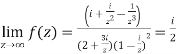
Continuity- A function w = f(z) is said to be continuous at z = 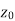 , if
, if
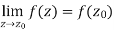
Also if w = f(z) = u(x , y) + iv(x , y) is continuous at z = 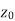 then u(x , y), v(x , y) are also continuous at z =
then u(x , y), v(x , y) are also continuous at z = 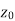 .
.
Differentiability-
Let f(z) be a single valued function of the variable z, then
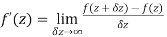
Provided that the limit exists and has the same value for all the different ways in which 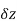 approaches to zero.
approaches to zero.
Example-2: if f(z) is a complex function given below, then discuss 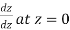
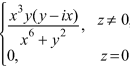
Sol. If z→0 along radius vector y = mx
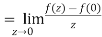
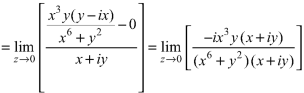
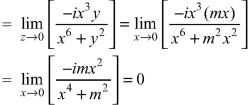
But along 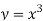 ,
,
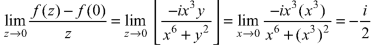
In different paths we get different value of 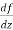 that means 0 and –i/2, in that case the function is not differentiable at z = 0.
that means 0 and –i/2, in that case the function is not differentiable at z = 0.
A function 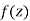 is said to be analytic at a point
is said to be analytic at a point 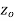 if f is differentiable not only at
if f is differentiable not only at 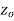 but an every point of some neighborhood at
but an every point of some neighborhood at 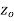 .
.
Note-
1. A point at which the function is not differentiable is called singular point.
2. A function which is analytic everywhere is called an entire function.
3. An entire function is always analytic, differentiable and continuous function.( converse is not true)
4. Analytic function is always differentiable and continuous but converse is not true.
5. A differentiable function is always continuous but converse is not true.
The necessary condition for f(z) to be analytic-
f(z) = u + i(v) is to be analytic at all the points in a region R are-
1. 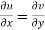 …………. (1)
…………. (1)
2. 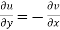 ……...…. (2)
……...…. (2)
Provided 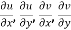 exists
exists
Equation (1) and (2) are known as Cauchy-Riemann equations.
The sufficient condition for f(z) to be analytic-
f(z) = u + i(v) is to be analytic at all the points in a region R are-
1. 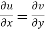 …………. (1)
…………. (1)
2. 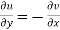 ……...…. (2)
……...…. (2)
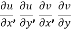 are continuous function of x and y in region R.
are continuous function of x and y in region R.
Important note-
1. If a function is analytic in a domain D, then u and v will satisfy Cauchy-Riemann conditions.
2. C-R conditions are necessary but not sufficient for analytic function.
3. C-R conditions are sufficient if the partial derivative are continuous.
State and prove sufficient condition for analytic functions
Statement – The sufficient condition for a function 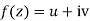 to be analytic at all points in a region R are
to be analytic at all points in a region R are
1 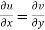
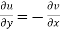
2 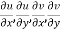 are continuous function of x and y in region R.
are continuous function of x and y in region R.
Proof :- Let f(z) be a simple valued function having 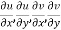 at each point in the region R. Then Cauchy-Reimann equation are satisfied by Taylor’s Theorem
at each point in the region R. Then Cauchy-Reimann equation are satisfied by Taylor’s Theorem
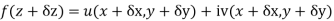
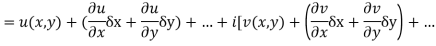
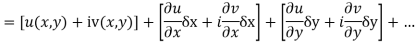
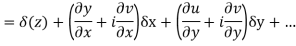
Ignoring the terms of second power and higher power
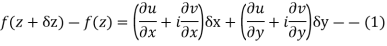
We know C-R equation
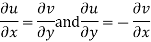
Replacing 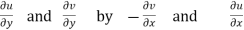
Respectively in (1) we get
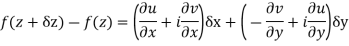
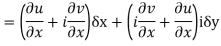
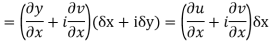
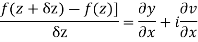
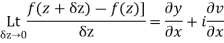
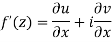
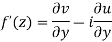
Show that 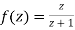 is analytic at
is analytic at 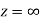
Ans The function f(z) is analytic at 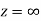 if the function
if the function 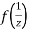 is analytic at z=0
is analytic at z=0
Since 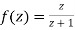
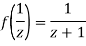
Now 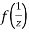 is differentiable at z=0 and at all points in its neighbourhood Hence the function
is differentiable at z=0 and at all points in its neighbourhood Hence the function 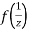 is analytic at z=0 and in turn f(z) is analytic at
is analytic at z=0 and in turn f(z) is analytic at 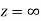
Example-1: If w = log z, then find 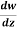 . Also determine where w is non-analytic.
. Also determine where w is non-analytic.
Sol. Here we have 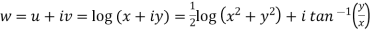
Therefore-
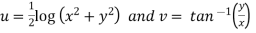
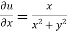 and
and 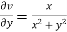
Again-
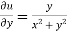
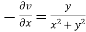
Hence the C-R conditions are satisfied also the partial derivatives are continuous except at (0 , 0).
So that w is analytic everywhere but not at z = 0
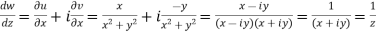
Example-2: Prove that the function 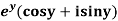 is an analytical function.
is an analytical function.
Sol. Let 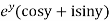 =u+iv
=u+iv
Let 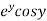 =u and
=u and 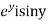 =v
=v
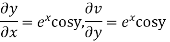
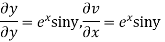
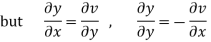
Hence C-R-Equation satisfied.
Example-3: Prove that 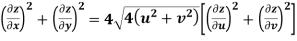
Sol. Given that
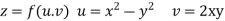
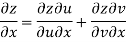
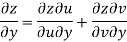
Since 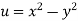

V=2xy

Now 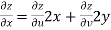
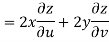
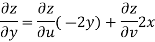
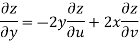
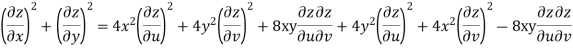
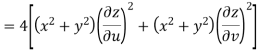
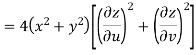
But 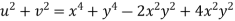
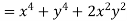
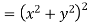
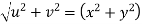
Hence 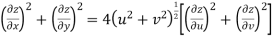
Example-4: Show that polar form of C-R equations are-
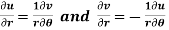
Sol. z = x + iy = 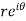
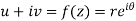
U and v are expressed in terms of r and θ.
Differentiate it partially w.r.t. r and θ, we get-
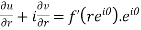
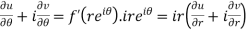
By equating real and imaginary parts, we get-
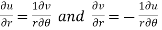
Theorem; The necessary condition for a function 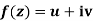 to be analytic at all the points in a region R are
to be analytic at all the points in a region R are
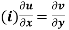 (ii)
(ii) 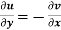
Provided, 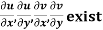
Proof:
Let 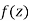 be an analytic function in region R.
be an analytic function in region R.
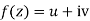
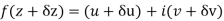
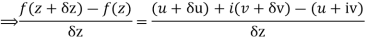
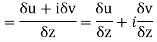
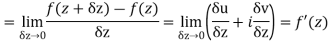
Along real axis
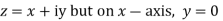
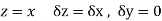
Then f’(z), becomes-
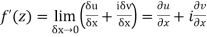 ………… (1)
………… (1)
Along imaginary axis
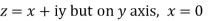
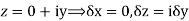
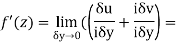
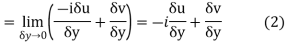
From equation (1) and (2)
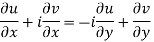
Equating real and imaginary parts
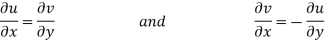
Therefore-
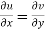 and
and 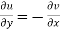
These are called Cauchy Riemann Equations.
Example-1: Check whether the function w = sin z is analytic or not.
Sol. Here-
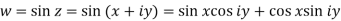
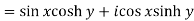
Now-
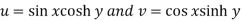
And
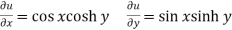
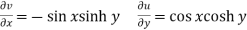
Here we see that C-R conditions are satisfied and partial derivatives are continuous.
Example-2: Prove that the real and imaginary parts of the function w = log z satisfies C-R equations.
Sol.
We put 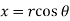 and
and 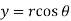 to separate the real and imaginary parts of log z.
to separate the real and imaginary parts of log z.
w = log z = log (x + iy)
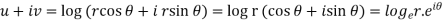
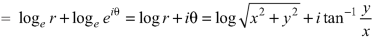
Here 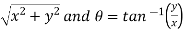
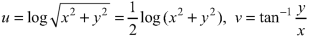
On differentiating u and v, we get-
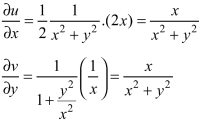
From the above two equations, we have-
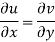
Again differentiating u and v, we get-
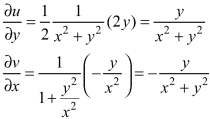
We have form the above equation-
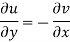
Hence the C-R condition is satisfied.
If the sense of the relation as well as magnitude of the angle is preserved the transformation is said to be conformal.
Example-1: Find the conformal transformation of  .
.
Answer. Let 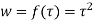
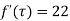
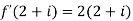
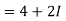
Theorem: If W=f(z) represents a conformal transformation of a domain D in the z-plane into a domain D of the W plane then f(z) is an analytic function of z in D.
Proof: We have u + iv = u (x, y) + iv (x, y)
So that u=u (x, y) and v=v (x, y)
Let ds and 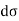 denote elementary arc length in the z-plane and w-plane respectively Then
denote elementary arc length in the z-plane and w-plane respectively Then
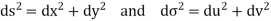
Now 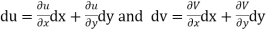
Hence 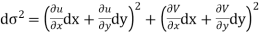
Or 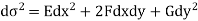
Where 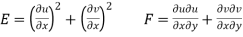
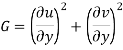
Now 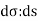 is independent of direction if
is independent of direction if
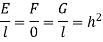
Where h depends on x and y only and is not zero. Thus the conditions for an isogonal transformation
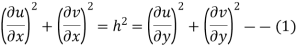
And 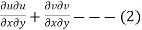
The equation are satisfied if we get
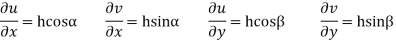
Then substituting these values in 2 we get
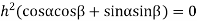
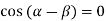
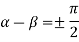
Taking 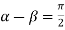 i.e.
i.e. 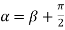
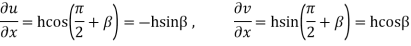
Also 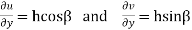
Hence 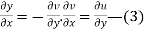
Similarly 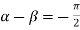 i.e.
i.e. 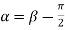
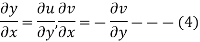
The equation (4) are the well known Cauchy -Reimann
Conformal mapping
Show that the mapping 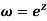 is conformal in the whole of the z plane.
is conformal in the whole of the z plane.
Sol.
Let z=x+iy
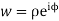
Then 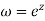
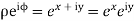
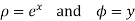
Consider the mapping of the straight line x=a in z plane the w plane which gives 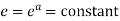 which is a circle in the w plane in the anticlockwise direction similarly the straight line y=b is mapped into
which is a circle in the w plane in the anticlockwise direction similarly the straight line y=b is mapped into 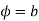 which is a radius vector in the w plane.
which is a radius vector in the w plane.
The angle between the line x=a and y=b in the z plane is a right angle. The corresponding angle in the w plane between the circle e = constant and the radius vector 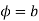 is also a right angle which establishes that the mapping
is also a right angle which establishes that the mapping 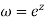 is conformal.
is conformal.
Example: Show that the curve u = constant and v = constant cut orthogonally at all intersections but the transformation w = u + iv is not conformal. Where-
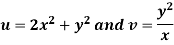
Sol.
Let 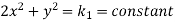 …………. (1)
…………. (1)
Differentiate (1), we get-
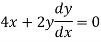
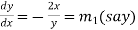 …………… (2)
…………… (2)
Now-
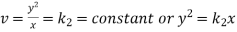 …………….. (3)
…………….. (3)
Differentiate (3), we get-
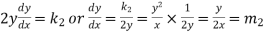 ………. (4)
………. (4)
As we know that for the condition for orthogonallity, from (2) and (4)
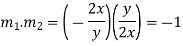
So that these two curves cut orthogonally.
Here,
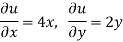
And
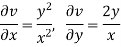
Here the C-R equation is not satisfied so that the function u + iv is not analytic.
Hence the transformation is not conformal.
Bilinear transformation is a correction of backwards difference method.
The bilinear transformation (also known as Tuatn’s method transformation) is defined as substitution:
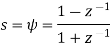
Example 1:
Find the bi-linear transformation which aps points z=2,1,0 ontpo the points w=1,0,i
Sol.
Let 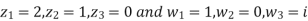
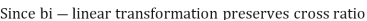
Thus we have
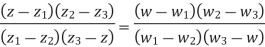
= 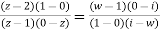
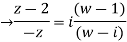

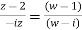
Example 2:
How that the bilinear transformation w= 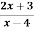 transforms
transforms 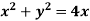 in the z-plane to 4u+3=0 in w-plane.
in the z-plane to 4u+3=0 in w-plane.
Sol.
Consider 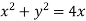 the circle in z-plane
the circle in z-plane

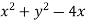 = 0
= 0
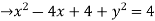

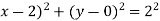
Thus, centre of the circle is (h,k) c(2,0) and radius r=2.
c(2,0) and radius r=2.
Thus in z-plane it is given as 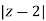 =2....(1)
=2....(1)
Consider w= 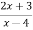
W(z-4) = 2z+3
Wz-4w=2z+3
Wz-2z=4w+3
Z(w-2) = (4w+3)
 z =
z = 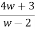
z-2 = 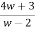 - 2
- 2
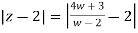
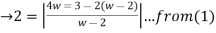
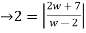
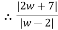
If a function f(z) is analytic and its derivative f’(z) continuous at all points inside and on a closed curve c, then 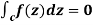
Proof: Suppose the region is R which is closed by curve c and let-
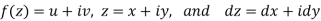
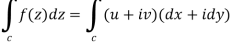
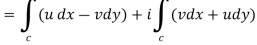
By using Green’s theorem-
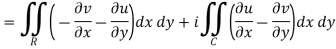
Replace 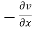 by
by 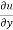 and
and 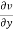 by
by 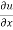 -
-
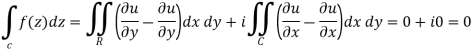
So that-
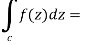
Example-1: Evaluate 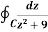 where C is |z + 3i| = 2
where C is |z + 3i| = 2
Sol.
Here we have-
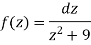
Hence the poles of f(z),
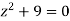
Note- put determine equal to zero to find the poles.
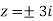
Here pole z = -3i lies in the given circle C.
So that-

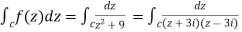
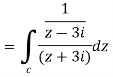
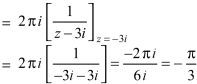
Example 2:
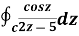 where C =
where C = 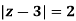
Sol.
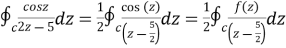 where f(z) = cosz
where f(z) = cosz
= 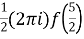 by cauchy’s integral formula
by cauchy’s integral formula
= 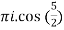
Example 3:
Solve the following by cauchy’s integral method:
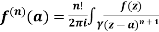
Solution:
Given,
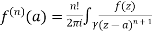
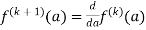
= 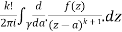
= 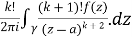
= 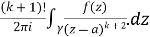
Cauchy’s integral formula-
Cauchy’s integral formula can be defined as-
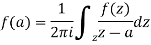
Where f(z) is analytic function within and on closed curve C, a is any point within C.
Example-1: Evaluate 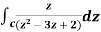 by using Cauchy’s integral formula.
by using Cauchy’s integral formula.
Here c is the circle |z - 2| = 1/2
Sol. It is given that-
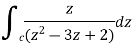
Find its poles by equating denominator equals to zero.
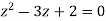
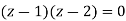
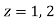
There is one pole inside the circle, z = 2,
So that-
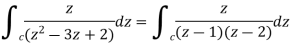
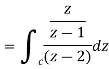
Now by using Cauchy’s integral formula, we get-
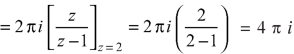
Example-2: Evaluate the integral given below by using Cauchy’s integral formula-

Sol. Here we have-
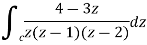
Find its poles by equating denominator equals to zero.
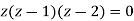
We get-
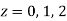
There are two poles in the circle-
Z = 0 and z = 1
So that-

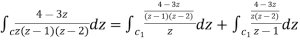
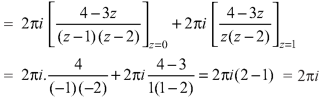
Example-3: Evaluate 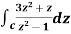 if c is circle |z - 1| = 1.
if c is circle |z - 1| = 1.
Sol. Here we have-
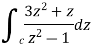
Find its poles by equating denominator equals to zero.
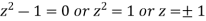
The given circle encloses a simple pole at z = 1.
So that-

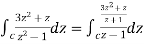
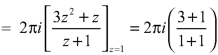
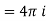
If 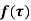 is analytic in a closed curve c except at a finite number of poles within c then
is analytic in a closed curve c except at a finite number of poles within c then
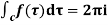 [Sum of residue at the pole within c]
[Sum of residue at the pole within c]
Example: Evaluate the following integral using residue theorem
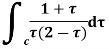
Where c is the circle.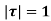 .
.
Sol. The poles of the integral are given by putting the denominator equal to zero
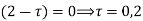
The integral is analytic on 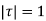 and all points inside except
and all points inside except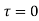 as a pole at
as a pole at 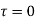 is inside the circle
is inside the circle 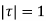
Hence by residue theorem
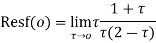
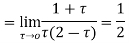
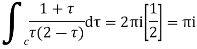
Example: Evaluate 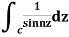 where c;|z|=4
where c;|z|=4
Sol.
Here f(z)=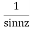
Poles are 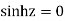
Sin iz=0
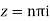
Poles 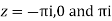
Lie inside the circle |z|=4
The given function 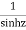 is of the form
is of the form 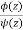
Its pole at z=a is 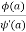
Residue (at 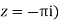
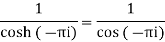
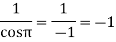
Residue at z=0=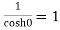
Residue at 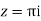 =
=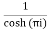
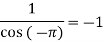
Residue at 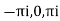 are
are
Respectively -1,1 and -1
Hence the required integrand
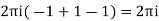
Example: Evaluate 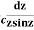 : c is the unit circle about the origin.
: c is the unit circle about the origin.
Sol.
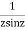 =
=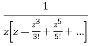
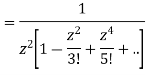
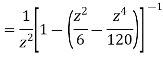
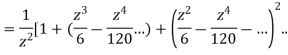
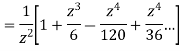
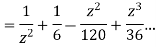
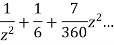
This shows that z=0 is a pole of order 2 for the function 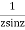 and the residue of the poles is zero(coefficient of 1/z)
and the residue of the poles is zero(coefficient of 1/z)
Now the pole at z=0 lies within c

Example: Evaluation of definite integrand
Show that 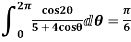
Sol.
I= 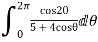
Real part of 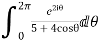
Now I= 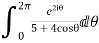 =
=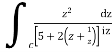
Putting z=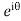 where c is the unit circle |z|=1
where c is the unit circle |z|=1
I=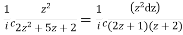
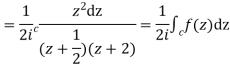
Now f(z) has simple poles at 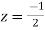 and z=-2 of which only
and z=-2 of which only 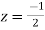 lies inside c.
lies inside c.
Residue at 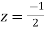 is
is 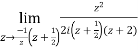
=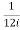
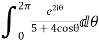 =
=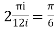
Now equating real parts on both sides we get
I=
- Prove that
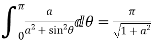
Solution Let 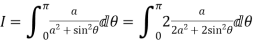
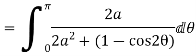
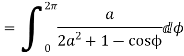
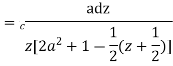
Putting 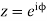 where c is the unit circle |z|=1
where c is the unit circle |z|=1
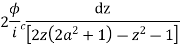
2ai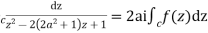
Poles of f(z) are given by the roots of
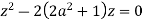
Or 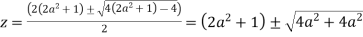
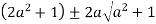
Let 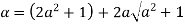
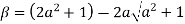
Clearly 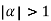 and since
and since 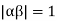 we have
we have 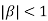 Hence the only pole inside c is at z=
Hence the only pole inside c is at z=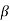
Residue (at 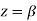 )
)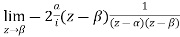
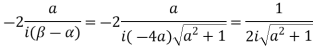
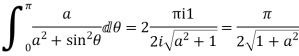
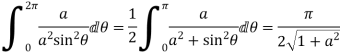
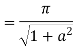
Example: Evaluate 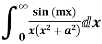
Sol.
Consider 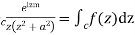
Where c is the closed contour consisting of
1) Real axis from 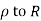
2) Large semicircle in the upper half plane given by |z|=R
3) The real axis -R to 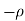 and
and
4) Small semicircle given by |z|=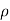
Now f(z) has simple poles at z=0 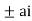 of which only z=
of which only z=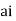 is avoided by indentation
is avoided by indentation
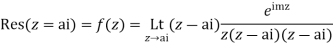
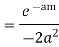
Hence by Cauchy’s Residue theorem
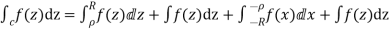
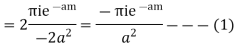
Since 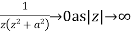 and
and
Hence by Jordan’s Lemma 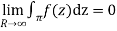
Also since 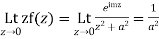
Hence 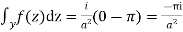
Hence as 
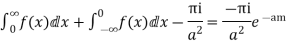
Equating imaginary parts we get
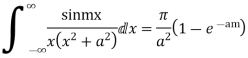
Example: Prove that 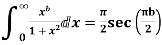
Sol.
Consider 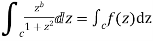
Where c is the contour consisting of a large semicircle in the upper half plane indented at the origin as shown in the figure
Here we have avoided the branch point o, of 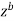 by indenting the origin
by indenting the origin
Then only simple of f(z) within c is at z=i
The residue(at z=i) =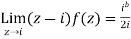
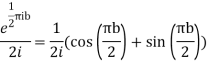
Hence by residue theorem
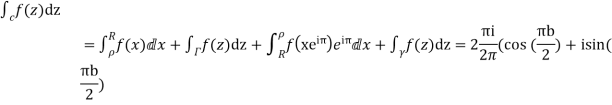
Since 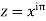 on -ve real axis.
on -ve real axis.
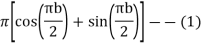
Now 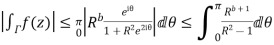
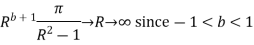
Similarly 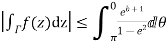
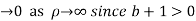
Hence when 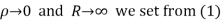
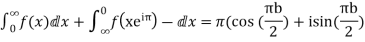
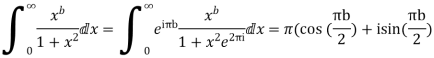
Equating real parts we get
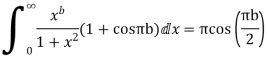
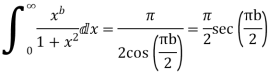
Reference Books:
1. Erwin Kreyszig, “Advanced Engineering Mathematics”, Wiley India,10th Edition.
2. M.D. Greenberg, “Advanced Engineering Mathematics”, Pearson Education, 2 nd Edition.
3. Peter. V and O‟Neil, “Advanced Engineering Mathematics”, Cengage Learning,7th Edition.
4. S.L. Ross, “Differential Equations”, Wiley India, 3rd Edition.
5. S. C. Chapra and R. P. Canale, “Numerical Methods for Engineers”, McGraw-Hill, 7th Edition.
6. J. W. Brown and R. V. Churchill, “Complex Variables and Applications”, McGraw-Hill Inc, 8th Edition.