Unit 3

D.C. Machines (Part–1)

3.1 Construction, Main Parts, Magnetic Circuits, Poles, Yoke, Field Winding, Armature Core

They convert mechanical energy into electrical energy. The energy conversion is based on the principle of production of induced emf. The construction and working are explained below.

Construction – A simple generator is shown below, the essential parts of which are

1)     Yoke – It is the outer frame of machine which carries the magnetic flux produced by poles and also provides mechanical support to the poles. The yoke is generally made of cast steel or rolled steel.

2)     Pole shoes – They are made up of thin lamination of annealed steel, which are piled up under hydraulic pressure. They spread out the flux in the air gap. They reduce the reluctance as they have large cross-sectional area.

3)     Held coils –They are the copper wire which are wounded around the core, the flux is produced when the current passes through these coils.

4)     Armature core – It provides the low reluctance path to the flux through the armature. It carries the conductor coils and makes them to rotate, which in turn tells the magnetic flux produced. It is cylindrical in shape and made of circular steel sheets.

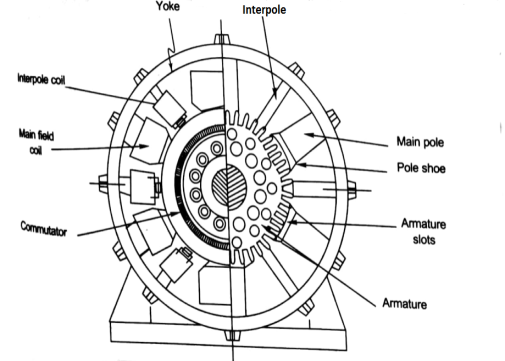
Fig. 1: Cross Section of DC Machine

5)     Armature Windings – These windings are arranged in armature slots, the slots are lined with tough insulating material. The useful EMF is encouraged in these findings and is received across brushes.

6)     Commutator - It collects the current from armature and supplies to the load. It is cylindrical in shape. It periodically reverses the current direction between the rotor and external circuit. It is composed of multiple metal segments insulated from each other by thin layer of Mica. The number of segments is equal to number of armature coil.

7)     Brushes and bearings - The brushes are usually made of carbon or graphite. The main function of brushes is to collect current from commutator. They are housed in brush holders and mounted on a spindle. The number of brushes per spindle depends upon the magnitude of the current to be collected from commutator.

Key takeaway

They convert mechanical energy into electrical energy. The energy conversion is based on the principle of production of induced emf

3.2 Armature Windings: Simple Lap and Wave Winding, Commutator and Brush Assembly

Armature windings

Simple lap winding –

1)     In this type of winding, the back and front pitches are odd and opposite in sign. They have difference of 2 or multiple of 9r.

2)     The back and front pitches should be equal to pole pitch.

3)     Average pitch,

4)     Commutator pitch, Yc = ±m.

5)     Resultant pitch, YR = YB – YF.

6)     The number of slots is half the number of coil sides.

7)     YB = YF ± 2m (m=1, simplex wave winding)

If YB> YF, YB = YF + 2 (Right-handed winding). Yc = +1

If YB< YF, YB = YF – 2 (Left-handed winding). Yc = -1.

8)     They are useful for low voltage, high current generators.

Simple Wave Winding

1)     The back and front pitches both are odd and of same sign.

2)     YB and YF are nearly equal to the pole pitches.

3)     Resultant pitch, YR = YB + YF

4)     Commutator pitch, YC= YA (for lap winding YC = ±1).

5)     Average pitch,

6)     The number of coils,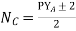

7)     The number of armature parallel paths =2m

m = multiplicity of windings.

8)     They are suitable for low current and high voltage generators.

9)     It gives more emf than lap winding.

Key takeaway

For lap winding

1)     The back and front pitches should be equal to pole pitch.

2)     Average pitch,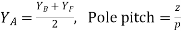

3)     Commutator pitch, Yc = ±m.

For wave winding

1)     The number of armature parallel paths =2m

m = multiplicity of windings.

3.3 Generating Action

The basic circuit model for a dc machine is shown below:

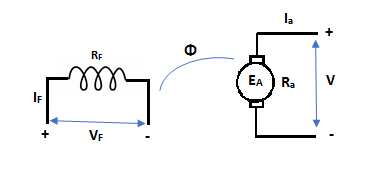
Fig. 2: Generating Action

The machine operates in generating mode when the armature current is in the direction of induced emf Ea.

V = Ea – Ia Ra  Ea> V

Pmech = Ea Ra = Pelect

The output power,

P0 = VIa

EaIa – VIa = Ia2 Ra

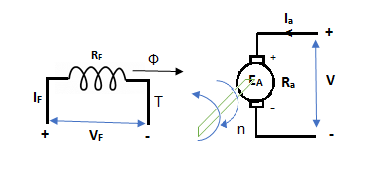
Fig. 3: Generation of Torque in armature

Key takeaway

In this mode, the torque of electromagnetic origin is in opposite direction of rotation of armature.

[Pmech]gross = Shaft power = [Pmech]net + Rotational loss.

3.4 E.M.F. Equation

The average coil emf

Wm = armature speed rad/s.

As parallel path emf is equal to armature emf,

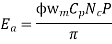
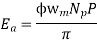
Np = turns / parallel path =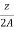

Z = Total armature conductors

A = Number of parallel paths.

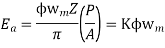
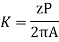
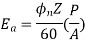
n = armature speed rpm

3.5 Magnetization Curve

1. Separately Excitation

It is the curve which relates the field current and armature terminal voltage on open circuit. For generating mode, we already know that generated emf is directly proportional to flux per pole and speed of armature.

The circuit is given below-

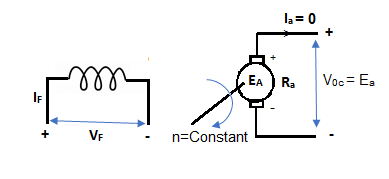
Fig. 4: Separately Excited DC Motor

From above figure,

Voc = Ea

The magnetization characteristic of dc machines is determined by measuring Voc at rated armature speed and gradually increasing If from zero till Voc reaches above rated value of machine.

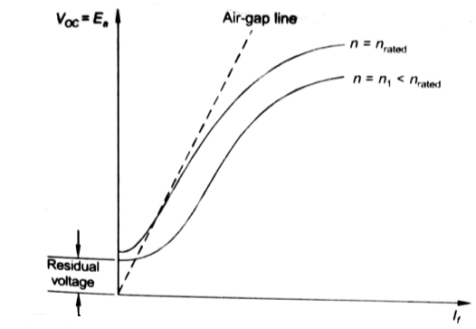
Fig. 5: Speed current characteristic curve

From above curve, we can conclude

1)     A small residue voltage is present when field is unexcited.

2)     The field current If increases from initial value, the flux and hence generated emf is increased.

3)     The air-gap line is the magnetic behaviour of machines air-gap. The iron being unsaturated in this region consumes negligible power.

4)     The open circuit cost is conducted by exciting the main field winding.

5)     The equivalent main field current is given

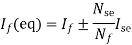
Nf, main field turns

If, main field current

Nse, main series turn

Ise, main series current

As induced emf is reduced by demagnetizing effect of armature reaction in saturation region of curve. So, the modified magnetization characteristics are shown below with Ia = 0, Ia = Ia1, Ia = Ia2.

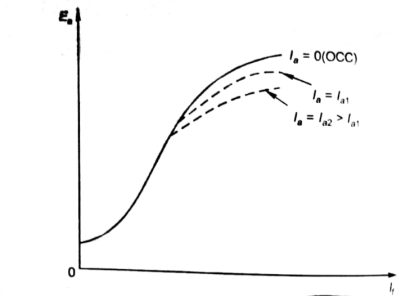
Fig. 7: Armature reaction in Speed current characteristics

B.     Self-excitation

The magnetization curve relates the no load voltage to the field current. The circuit is shown below

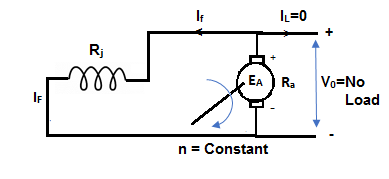
Fig. 8: Self Excited DC motor

The field is introduced after the armature has been brought to rated speed. Just the moment after switching on the field, residue armature voltage exists which causes small value of field current. A fine steady state value is attained because of the saturation state of machines magnetic circuit. The magnetization curve is shown below:

The current in armature can be related to field current as

Ia = If

V = Ea- If Ra

In this case, field current is very small, so

V ≈ Ea (If) [magnetization characteristic]

For field current,

V = If Rf

• The intersection point P on Rf line gives the values of no-load voltage Vo and corresponding field current If.
• Vo can be adjusted by varying Rf.
• Further, the above plot can be assessed by keeping armature speed constant and varying Rf. The plot is shown below.

Fig. 9: Magnetising Curve

• As Rf is increased, the value of Vo decreases.
• Value of Vo is not defined for (Rf3 = Rfc).
• As the value of field resistance here is increased to high value but does not produce high Vo, rather its value is close to residue voltage. Hence, machine field fails to excite and this value of resistance is called critical resistance Rc.

• Now keeping Rf fixed and varying armature speed, the plot is shown below:

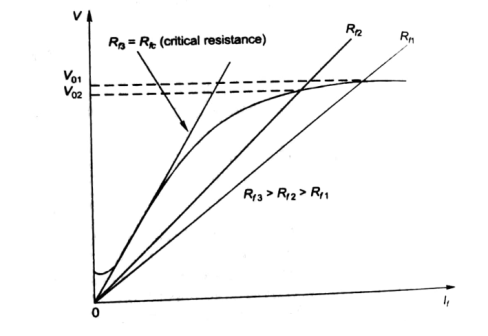
Fig. 10: Characteristic curve with Rf fixed

• As the speed decreases, the open circuit characteristics also decrease proportionally.
• At critical Speed, the generator fails to excite.

Key takeaway

For separately excited DC Motor Voc = Ea

For Self-Excited DC Motor

In this case, field current is very small, so

V ≈ Ea (If) [magnetization characteristic]

For field current,

V = If Rf

3.6 Flashing of Generator

As the induced EMF (in the armature due to the field connections) due to residue magnetism destroys the residue magnetism giving a negative feedback. So, to overcome this we can either reverse the field connections to armature or the direction of rotation can be reversed. But in large generators with permanent connections, the problem is solved by exciting the filed temporarily from a battery source.

3.7 Motoring Action

In this mode, the armature current Ia flows opposite to the emf induced i.e. Ea. The basic circuit showing this mode is below:

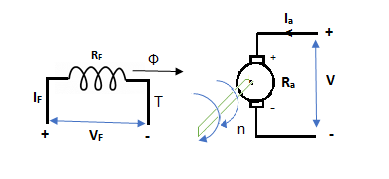
Fig. 11: DC Motor

(Ea – Eb) is called as back emf here as it opposes the armature emf.

V = Ea + IaRa

Electrical power connected to mechanical form

Pelec / net = EaIa

Power input, Pi = V Ia

V Ia – EaIa = Ia2Ra = armature copper loss.

Key takeaway

The back emf is given as

Eb =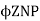

3.8 Types of DC Motors

1)     Shunt motor – In this, the field winding is connected in parallel with the armature.

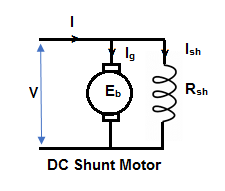
Fig. 12: DC Shunt Motor

The input current I = Ia + Ish

For field winding, V = IshRsh

For armature, V = Eb + IaRa

Ia = armature current

Ish = shunt field current

V = input voltage

I = Input current

Power Input = Mechanical power + losses in armature + losses in field

VI = Pmech + Ia2Ra + Ish2Rsh

Pmech = VI – VIsh - = Ia2Ra

= V(I – Ish) – Ia2Ra

= VIa - = Ia2Rsh = (V – IaRa)Ia

Pmech = EaIa

2)     Series motor – In this, the field winding is connected in series with the armature.

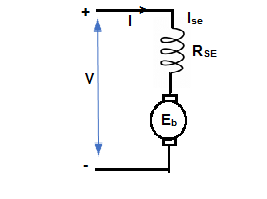
Fig. 13: DC Series Motor

Ise = series field current

I = Ia = Ise

V = Ea + I(Ra + Rse)

VI = EaI + I2(Ra + Rse)

VI = Pmech + I2 Ra + I2Rse

Pmech = Ea I

3)     Compound Motor – It is a type of dc motor which had both shunt and series field windings.

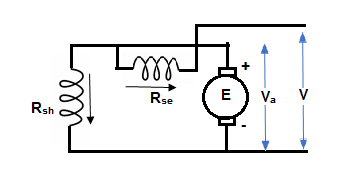
Fig. 14: Compound Motor

V = Ea ± Ia (Ra + Rse)

IL = Ia ± IF

They are basically of 2 types- long shunt and short shunt.

Key takeaway

For Shunt Motor

The input current I = Ia + Ish

For field winding, V = IshRsh

For Series Motor

Ise = series field current

I = Ia = Ise

For Compound Motor

V = Ea ± Ia (Ra + Rse)

IL = Ia ± IF

3.9 Significance of Back E.M.F.

In a DC motor when the armature rotates the conductors also rotate and hence cut the flux. According to the lower electromagnetic induction, the induced EMF is in the opposite direction (by Fleming’s Right hand rule) to the applied voltage. As it has opposite direction so it is referred to as back EMF (Eb).

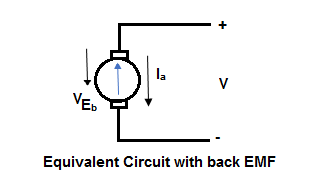
Fig. 15: Equivalent Circuit with Back EMF

This back emf Eb is like battery put across main supply. This back emf is given as

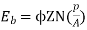  N is in rpm.

• If speed of armature is high, Eb is large.
• If speed of armature is low, Eb is less.

Motor Torque

1)     Armature Torque (Ta) of motor –

Power developed = Ta × 2πN     W

As electrical power is converted to mechanical =EbIb

So, power developed = Power converted

Ta × 2πN = EbIb

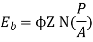
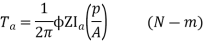
We can also conclude from the above eqn.

For series,

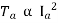
For shunt,

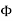is constant practically.

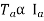
2)     Shaft Torque (Tsh) –

The torque doing useful work is called as shaft torque, Tsh.

Motor output =Tsh × 2πN

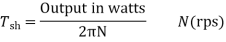
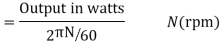
Due to iron and friction losses in motor Ta – Tsh difference torque exists called as lost torque.

Key takeaway

For series,

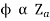
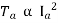
For shunt,

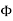is constant practically.

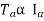
For Shunt

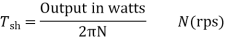
Q. 1 A 4 pole dc generator runs at 650 rpm and generates emf of 220V. The armature is wave wound and has 790 conductors. If total flux/pole is 0.0145 Wb in each pole, find leakage coefficient.

Soln.  Leakage coefficient =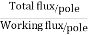

Working flux is given as

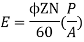
A = 2 for simple wave winding.

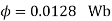
Leakage coefficient =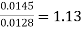

Q. 2 A 4 pole lap wound dc shunt generator has a useful flux per pole of 0.05 Wb. The armature winding consists of 200 turns each of 0.06 u ohm resistance. Calculate the terminal voltage when running at 900 rpm with armature current of 50 A.

Soln. Terminal voltage V =Ea – Ia Ra

Ia Ra = 50×Ra.

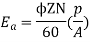
Z = 200×2=400 (each turn has two sides).

N = 900 rpm 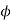  = 0.05 Wb  P = A = 4

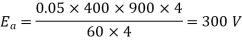
Total resistance of 200 turns = 200 × 0.004 = 0.8 ohm

As there are 4 parallel paths, so resistance of each path = 0.8/4 = 0.2 ohm

There are 4 resistances in parallel of each of 0.2 ohm

Ra = 0.2/4 = 0.05 ohm

Ia Ra = 50×0.05 = 25 V

V = Ea – Ia Ra = 300 – 25 = 275 V

Q. 3 A 220 V 4 pole wave wound dc series motor has 780 conductors on its armature. It has armature and series field resistance of 0.75 ohm. The motor takes a current of 30A. Find the speed and gross torque developed if flux/pole is 20 mWb?

Soln.  Back emf,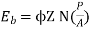

Eb = V – IaRa = 220 – (30×0.75) = 197.5 V

197.5 = 20 × 10-3 ×780×N×0.75

N = 16.88 ≈ 17

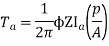
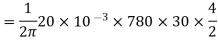
Ta = 158.97 Nm.

3.10 Torque equation

Average conductor force

Fav = Bav l Ic

Bav = avg. Flux density over pole.

l = active conductor length.

Force, F = ZFav = BavlIcZ

T = f.r

T = Bav l IC Zr

r = mean of r gap radius.

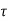Flux/pole = BavPl

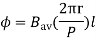
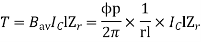
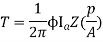
The torque is uniform for given flux/pole and armature current.

Key takeaway

The EMF equation is

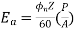
The torque is given as

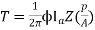Nm

3.11 Working at No-Load and On-Load Losses

Losses

1)     Copper loss –

Armature Cu loss = Ia2 Ra

Field Cu loss: a) For shunt = Ish2Rsh

b) For series = Ise2Rse

2) Magnetic loss

a) hysteresis loss: Wh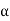B1.6max f

b) Eddy current loss: We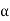  B2max f2

2)      Mechanical loss – They are basically the frictional losses at bearings and commutators.

3.12 Power Flow Diagram and Efficiency

Power flow diagram

Efficiency-

1)     Mechanical Efficiency

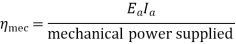
2)     Electrical efficiency

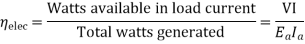
3)     Overall efficiency

3.13 Descriptive Treatment of Armature Reaction

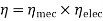
Armature Reactions

When armature of a DC Machine carries current, the distributed armature winding produces its own mmf which is known as armature reaction. The figure is shown below.

The nature of armature reaction in a DC machine is cross magnetizing with its axis along the (90° to main pole).

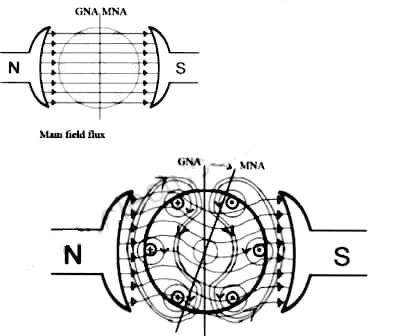
Fig. 16: Generation of Armature Reaction

MNA (Magnetic Neutral Axis) It is the axis along which no EMF generated in the armature conductors.

GNA (Geometrical Neutral Axis)  It is perpendicular to the field axis.

When DC machine is running the flux due to armature and field winding exists. The armature flux is dominant on the later and hence disturbing the main field flux. This effect is called armature reaction in DC machines.

Key takeaway

MNA (Magnetic Neutral Axis) It is the axis along which no EMF generated in the armature conductors.

GNA (Geometrical Neutral Axis)  It is perpendicular to the field axis.

Q. 1 A 4 pole, 210 V shunt motor has 450 lap wound conductor. It takes 32 A from supply mains and develops output power of 4.5 kW. The field takes 1 A. The armature resistance is 0.09 ohm and flux per pole is 30 mWb. Calculate speed and torque.

Soln. Ia = 32-1 = 31 n

Eb = V – Ia Ra = 210 - (0.09×31) = 207.21 V

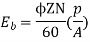
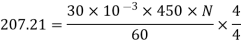
N = 920.9 rpm

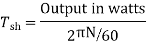
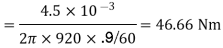
Q. 2 A 220 V, dc shunt motor has an armature resistance of 0.3 ohm and field resistance of 105 ohm. At no load speed is 1200 rpm and armature current is 2.3 A on application of rated load speed drops to 1120 rpm. Find the current and power input when motor delivers rated load.

Soln. N1 = 1200 rpm  Eb1 = 220 – (0.3×2.3) = 219.31 V

N2 = 1120 rpm  Eb2 = 220 – 0.3 Ia2

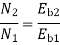
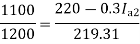
Ia2 = 37.93 A

Line current = Ia2 + Ish = 37.93 + (220/105) = 40 A

Power input = 220 × 40 = 8800 W

Q. 3 A 230 V shunt motor runs at 1000 rpm at no load and takes 6A. The total armature resistance is 0.2 ohm and field resistance is 210 ohm. Calculate the speed when loaded and taking 40 A. Assume flux constant.

Soln.
 

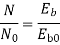
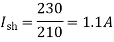
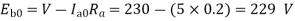
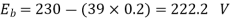
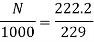
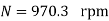
Q. 4 The armature resistance of a 15 kW, 230 V series motor is 0? 1 ohm, the brush voltage drop is 3 V and series field resistance is 0.05 ohm. The motor takes 60 A speed is 600 rpm. Calculate speed when current is 100 A.

Soln.

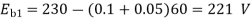
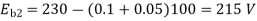
Φ1 60

Φ2 100

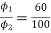
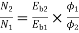
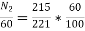
N2=350.22 rpm

Q.5 A 230V DC Shunt motor takes 4A at no load when running at 600 rpm. The field resistance is 100 ohms. The resistance of armature at standstill gives a drop of 6V across armature terminals when 10A were passed through it. Find i)Speed at no load (ii) Torque. Normal input of motor is 6kW

Soln

i)Speed

Ish= 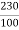=2.3A

F.L Power=6000

F.L line current= 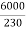=26.08A

Ia=26.08-2.3=23.78A

Ra=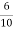=0.6Ω

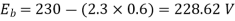
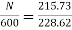
N=566.2 rpm

Ii)Torque Ta=

=

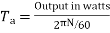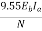
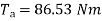
References:

1. [R1] A.E. Clayton and N. N. Hancock, “Performance and Design of Direct Current

Machines”, CBS Publishers, Third Edition.

2.     [R2] A.E. Fitzgerald, Charles Kingsley, Stephen D. Umans, “Electrical Machines”, Tata

McGraw Hill Publication Ltd., Fifth Edition.

3.     [R3] A.S. Langsdorf, “Theory and performance of DC machines”, Tata McGraw Hill.

4.     [R4] M.G. Say, “Performance and Design of AC. Machines”, CBS Publishers and

Distributors.

5.     [R5] SmarajitGhosh, “Electrical Machines”, Pearson Education, New Delhi.

6.     [R6] Charles I Hubert, “Electrical Machines Theory, Application, & Control”, Pearson

Education, New Delhi, Second Edition.