Unit-1
Numerical Computations, Errors, and Concept of the root of the equation
Introduction of numerical analysis-
Numerical analysis is a branch of mathematics that deals with solving difficult mathematical problems by using efficient methods
Sometimes the mathematical problems are very hard then an approximation to a difficult Mathematical problem is very important to make it easier to solve numerical approximation has become more popular and a modern tool there are three parts of numerical analysis. The first part of the subject is about the development of a method to a problem. The second part deals with the analysis of the method, which includes the error analysis and the efficiency analysis. Error analysis gives us an understanding of how accurate the result will be if we use the method and efficiency analysis tells us how fast we can compute the result
The third part of the subject is the development of an efficient algorithm to implement the method as a computer code.
Mathematical preliminaries-
Continuity of a function-
Continuity- suppose that a function f(x) is defined in the interval I, then it is said to be continuous at x=a, if
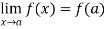
Differentiability- A function f(x) is said to be differentiable at x = a if
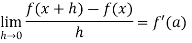
Exists where ‘a’ belongs to I
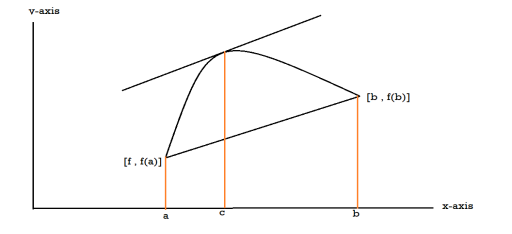
Rolle’s theorem-
Let f(x) be a continuous function on the bounded interval [a, b] and differentiable on (a, b). If f(a) = f(b) then-
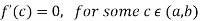
Mean value theorem for derivatives-
Suppose that f(x) be a function of x such that,
1. If it is continuous in [a, b]
2. If it is differentiable in (a, b)
Then there at least exists a value cϵ (a, b)
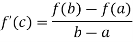
Proof:
Lets define a function g(x),
g(x) = f(x) – Ax ………………..(1)
Here A is a constant which is to be determined,
So that,
g(a) = g(b)
Now,
g(a) = f(a) – Aa
g(b) = f(b) – Ab
So,
g(a) = g(b),
f(a) – Aa = f(b) – Ab,
Which gives,
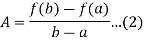
As right hand side of eq.(1) is continuous in [a,b], so that g(x) is continuous.
And right hand side of eq.(1) is differential in (a,b), so that g(x) is differentiable in (a,b).
And g(a) = g(b) , because of the choice of A.
Hence g(x) satisfies all the conditions of Rolle’s theorem.
So that,
There exists a value c such that a<c<b at which g’(c) = 0
Now, differentiate eq. (1) with respect to x, we get
g’(x) = f’(x) – A
Here we know that, x = c,
g’(c) = f’(c) – A
As g’(c) = 0, then
f’(c) – A =0
So that,
f’(c) = A,
From equation (2), we get
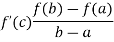
Hence proved
Example: Verify Lagrange’s mean value theorem for f(x) = (x-1)(x-2)(x-3) in [0,4].
Sol. As we see that the given function is a polynomial and we know that the polynomial is continuous in [0,4] and differentiable in (0,4).
f(x) = (x-1)(x-2)(x-3)
f(x) = x-6x²+11x-6
Now at x = 0, we get
f(0) = -6 and
At x = 4, we get.
f(4) = 6
Diff. The function w.r.t.x , we get
f’(x) = 3x²-6x+11
Suppose x = c, we get
f’(c) = 3c²-6c+11
By Lagrange’s mean value theorem,
f’(c) = 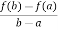 =
= 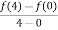 =
= 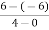 = 3
= 3
Now we get,
3c²-6c+11 = 3
3c²-6c+8 = 0
On solving the quadratic equation, we get
C = 2 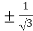
Here we see that the value of c lies between 0 and 4
Therefore the given function is verified.
Taylor’s formula-
Taylor’s theorem for a function f(x) can be expressed as an infinite series as follows-
f(x) = f(a) + (x – a)f’(a) + 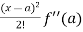 + ………
+ ………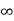 .
.
Example: Expand the function 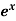 in ascending powers of (x – 1) by using Taylor’s theorem.
in ascending powers of (x – 1) by using Taylor’s theorem.
Sol. We know that the Taylor’s theorem for the function f(x) in ascending powers of (x – a) is,
f(x) = f(a) + (x – a)f’(a) + 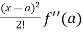 + ………
+ ………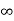 . ………….(1)
. ………….(1)
Here f(x) = 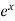 and a = 1
and a = 1
Now,
f’(x) = 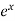 and f’(a) = e
and f’(a) = e
f’’(x) = 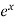 and f’’(a) = e
and f’’(a) = e
Put these values in equation (1),
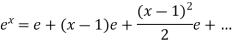
Take ‘e’ as common,
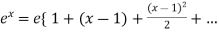
Which is the required expansion.
Floating-point form-
Let x be a non-zero real number. An n-digit floating-point number in base 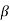 has the form-
has the form-
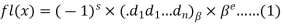
Where
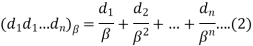
Is a 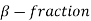 called mantissa,
called mantissa,
s = 0 or 1 called the sign, and e is an integer called the exponent.
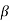 is called a radix.
is called a radix.
The point preceding 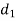 in equation (1) is called the radix point.
in equation (1) is called the radix point.
Note-
- When
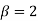 , the floating-point representation in equation (1) is called the binary floating-point representation.
, the floating-point representation in equation (1) is called the binary floating-point representation. - When
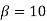 , is called the decimal floating-point representation.
, is called the decimal floating-point representation.
Normalization-
A floating-point number is said to be normalized if either 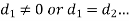 =
=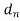 =0
=0
Rounding a chopping a number-
The chopped machine approximation of x is defined as-
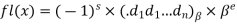
The rounded machine approximation of x is defined as-
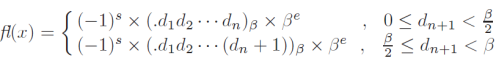
The numerical method provides a much wider range to solve the problem that is not possible by analytical methods. There are two ways to solve the numerical methods
a) Exact method: This provides the exact solution to the problem so there will be no error in this.
b) Trial and error or iteration or Approximation method: This will provide the approximate solution that contains a certain amount of error that can be tolerated.
Types of Error:
- Absolute Error:
The Approximate error is the numerical difference between the quantity of the exact solution and the approximate value of the solution.
Let X be the exact solution and the approximate value of the solution is denoted by 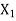 , then the absolute error is defined as
, then the absolute error is defined as
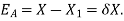
2. Relative Error:
The error obtained by dividing the approximate solution by the exact solution is known as relative error and is denoted by 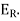
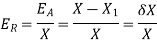
The percentage error is the 100 times of the relative error i.e.
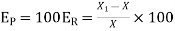 .
.
The absolute accuracy is magnitude absolute error.
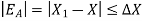 .
.
The relative accuracy is the magnitude of the relative error.
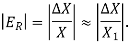
3. Algorithmic Error: A error caused due to rounding off the number or truncation is called an algorithmic error.
4. Truncation Error:
The truncation errors are caused by approximated values or by replacing the infinite process with a finite value.
Example: 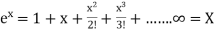 is replaced by
is replaced by 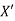 .
.
Then truncation error is 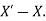
5. Round off Error:
The digit that is used to express a number is called significant digits or significant figures. Eg 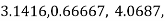 etc.
etc.
In numerical computation, the large number of digits cutting the usual figure is called rounding off. The rule to rounding off is
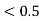 in the nth place, leave the nth digit unaltered.
in the nth place, leave the nth digit unaltered.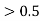 in the nth place, increase the nth digit =nth digit +1.
in the nth place, increase the nth digit =nth digit +1.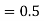 in the nth place, increase the nth digit=nth digit +1 if it is odd; otherwise, leave it unchanged.
in the nth place, increase the nth digit=nth digit +1 if it is odd; otherwise, leave it unchanged.
The number thus rounded-off is said to be correct to n significant figures.
The round-off error can be reduced by carrying out the computation to more significant figures at each step of the computation.
Example: Numbers –Round off
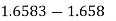 here 0.0003<0.0005 unchanged
here 0.0003<0.0005 unchanged
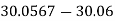 here 0.006>0.005 so, 5=5+1
here 0.006>0.005 so, 5=5+1
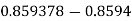 here 0.00007>0.00005 so, 8=8+1
here 0.00007>0.00005 so, 8=8+1
6. Error Propagation :
The error propagation is carried out in the number of steps to get the solution.
The approximate value of the two numbers X and Y is X’ and Y’
Then the absolute error is
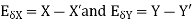
- Absolute error besides operation
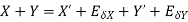
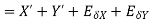
2. Absolute error in subtraction operation
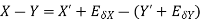
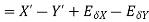
3. Absolute error in the multiplication operation
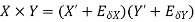
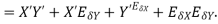
4. Absolute error in a division operation
The absolute error 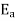 in the quotient of two numbers X and Y
in the quotient of two numbers X and Y
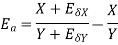
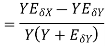
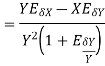
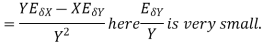
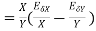 .
.
Example 1: An approximate value of 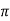 is given by
is given by 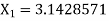 and its exact value is
and its exact value is 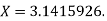 Find the absolute and relative errors.
Find the absolute and relative errors.
The absolute error is 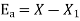
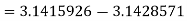
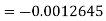 .
.
The relative error is
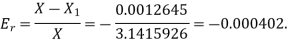
Example 2: Find the difference 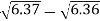 to three significant figures?
to three significant figures?
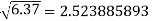
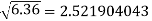
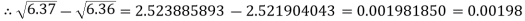
Correct to three decimal places.
Example 3: Round –off the following number to two decimal places
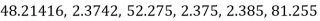
Number | Compare | Changes | Rounded-off number |
48.21416 | 0.004<0.005 | No change | 48.21 |
2.3 742 | 0.004<0.005 | No change | 2.37 |
52.275 | 0.005=0.005 | 0.07+0.01=0.08 | 52.28 |
2.375 | 0.005=0.005 | 0.07+0.01=0.08 | 2.38 |
2.385 | 0.005=0.005 | 0.08+0.01=0.09 | 2.39 |
81.255 | 0.005=0.005 | 0.05+0.01=0.06 | 81.26 |
Example 4: Find the absolute error if the number 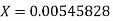 is truncated to three decimal places?
is truncated to three decimal places?
The given number is 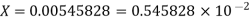
After truncating it to three decimal places the rounded value is 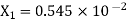
Therefore the absolute error is 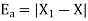
= 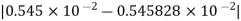
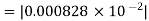
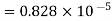 .
.
Generalized error formula (Derivation and Numerical)
Let-
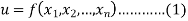
Be the function of 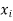 and let the error in each
and let the error in each 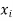 be
be 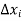 .
.
The error in u is given by-
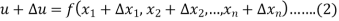
By using Taylor’s theorem we expand RHS-
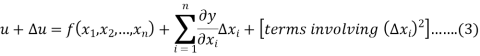
Let's assume that the errors in 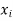 are small, so that the higher powers of
are small, so that the higher powers of 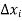 can be neglected,
can be neglected,
The above relation yields-
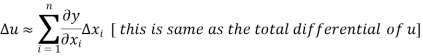
The formula for the relative error follows-
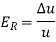
There are two types of equations Linear and Non-linear equations. Linear equations are those in which dependent variable y is directly proportional to independent variable x and is of degree one. On the other hand, a non-linear equation is those in which y does not directly proportional to x and of degree more than one.
Ex: 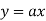 +b, where a and b are constant is a linear equation.
+b, where a and b are constant is a linear equation.
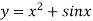 is a non-linear equation.
is a non-linear equation.

Algebraic Equation: If f(x) is a pure polynomial, then the equation 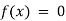 is called an algebraic equation in x.
is called an algebraic equation in x.
Ex: 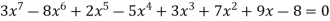
Transcendental Equation: If f(x) is an expression contain a function as trigonometric, exponential and logarithmic, etc. Then 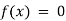 is called the transcendental equation.
is called the transcendental equation.
Ex 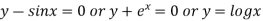
A non –linear equation can be solved by using various analytical methods. The transcendental equations and higher-order algebraic equations are difficult to solve even sometimes are impossible. Finding the solution of the equation means just to calculate its roots.
Numerical methods are often repetitive. They consist of repetitive calculation of the same process wherein each step the result of preceding values are used (substitute). This is known as the iteration process and is repeated till the result is obtained to the desired accuracy.
In the analytical methods used to solve equations; the exact value of the root is obtained whereas in the numerical method approximate value is obtained.
Method to find the roots-
Bisection method-
This method is consists of finding the root of the equation 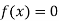 which lies between a and b (say).
which lies between a and b (say).
The function 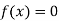 is a continuous function between a and b and f (a) and f (b) are of opposite signs then there is a least one root between a and b.
is a continuous function between a and b and f (a) and f (b) are of opposite signs then there is a least one root between a and b.
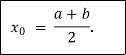 Suppose f (a) is negative and f (b) is positive, then the first approximate value of the root is
Suppose f (a) is negative and f (b) is positive, then the first approximate value of the root is
If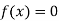 , then the correct root is
, then the correct root is 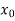 .But if
.But if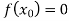 , then the root either lies between a and
, then the root either lies between a and 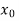 or
or 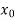 and b according to
and b according to 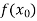 is positive or negative, we again bisect the interval as above and the process is repeated the root is found to the desired accuracy.
is positive or negative, we again bisect the interval as above and the process is repeated the root is found to the desired accuracy.
Example1 Find a real root of 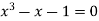 using bisection method correct to five decimal places.
using bisection method correct to five decimal places.
Let 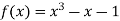 then by hit and trial we have
then by hit and trial we have
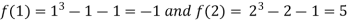
Thus 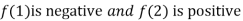 . So the root of the given equation should lie between 1 and 2.
. So the root of the given equation should lie between 1 and 2.
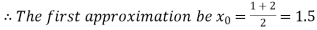
Now, 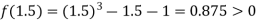
i.e. positive so the root of the given equation must lie between 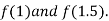
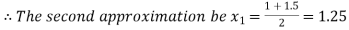
Now, 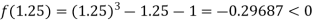
i.e. negative so the root of the given equation lies between 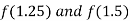
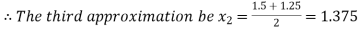
Now, 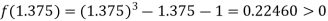
i.e. positive so the root of the given equation lies between 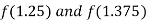
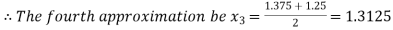
Now, 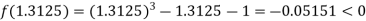
i.e. negative so that the root of the given equation lies between 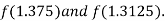
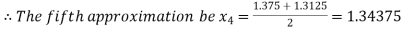
Now, 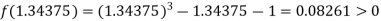
i.e. positive so that the root of the given equation lies between 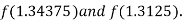
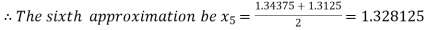
Now, 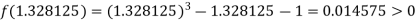
i.e. positive so that the root of the given equation lies between 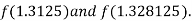
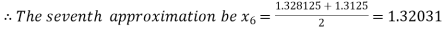
Now, 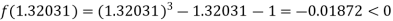
I.e. negative so that the root of the given equation lies between 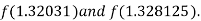
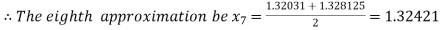
Now, 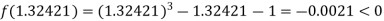
i.e. negative so that the root of the given equation lies between 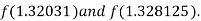
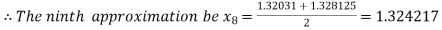
Hence the approximate root of the given equation is 1.32421
Example2 Find the root of the equation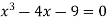 , using the bisection method.
, using the bisection method.
Let 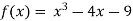 then by hit and trial we have
then by hit and trial we have
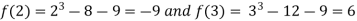
Thus 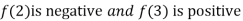 . So the root of the given equation should lie between 2 and 3.
. So the root of the given equation should lie between 2 and 3.
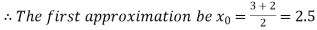
Now, 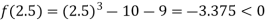
i.e. negative so the root of the given equation must lie between 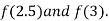
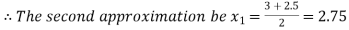
Now, 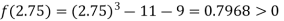
i.e. positive so the root of the given equation must lie between 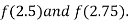
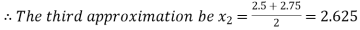
Now, 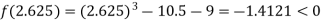
i.e. negative so the root of the given equation must lie between 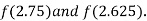
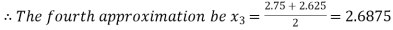
Now, 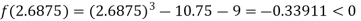
i.e. negative so the root of the given equation must lie between 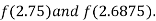
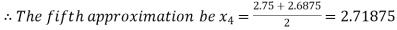
Now, 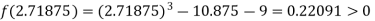
i.e. positive so the root of the given equation must lie between 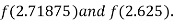
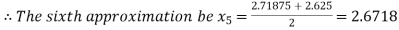
Now, 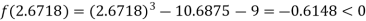
i.e. negative so the root of the given equation must lie between 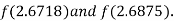
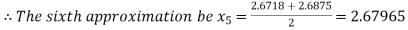
Hence the root of the given equation correct to two decimal places is 2.67965.
Descartes’ rule of sign-
According to this rule- A polynomial equation p(x) =, 0 can not have more positive roots than the number of changes in sign of its coefficients.
Similarly, p(x) = 0 cannot have more negative roots than the number of changes in sign of the coefficient of p(x).
Note-
- An equation of odd degree with real coefficient has at least one real root whose sign is opposite to that of the last term.
- An equation of even degree whose constant term has the sign opposite to that of the leading coefficient has at least two real roots one positive and another negative.
We can define the relationship between roots and coefficient of polynomial equation as-
Suppose 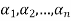 be n roots of the polynomial-
be n roots of the polynomial-
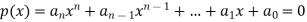
Then
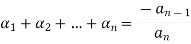
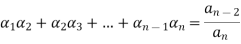
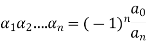
Example: Let us consider a polynomial equation-
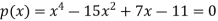
Now going from left to right there are changes between 1 and -15, between -15 and 7, and between 7 and -11.
The total number of changes is 3 and hence it can have the most 3 positive roots.
Now consider-
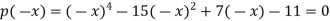
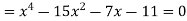
There is one change only between 1 and -15 hence the equation cannot have more than one negative root.
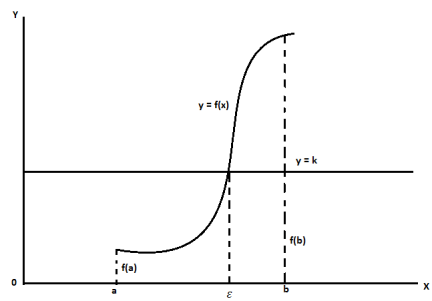
Intermediate value theorem-
Let f(x) be continuous in [a, b] and let k be any number between f(a) and f(b).
Then there exists a number 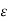 in (a, b) such that f(
in (a, b) such that f(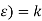
This method is the modified form of the Newton-Raphson method.
Let us consider a polynomial equation of degree ‘n’-
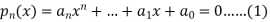
Suppose 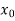 be an initial approximation to the root of
be an initial approximation to the root of 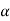 .
.
The Newton-Raphson iteration formula for improving this approximation-
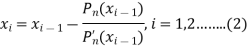
We shall be able to find both 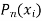 and
and 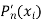 at any
at any 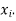
We will evaluate as-
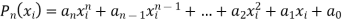
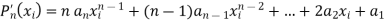
Because of a lot of computations involved and due to round off errors, this method is not efficient.
Let us consider the evaluation of 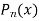 and
and 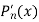 at
at 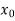 by using Horner’s method-
by using Horner’s method-
We have-
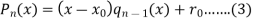
Where
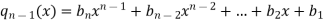
And
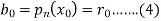
Now we shall find the derivative 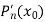 by using Horner’s method.
by using Horner’s method.
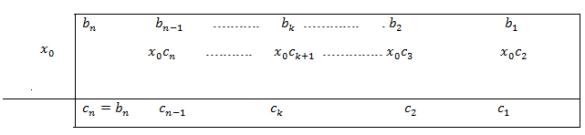
We divide 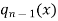 by
by 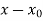 using Horner’s method,
using Horner’s method,
We write-
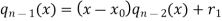
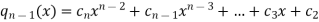
We get 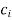 as given in table-
as given in table-
We have-
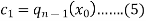
Now from equations (3) and (4), we have-
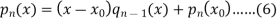
Now differentiate both sides of equation (6) w.r.t. x-
We get-
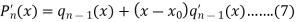
Putting 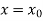 in equation (7), we get-
in equation (7), we get-
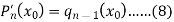
Comparing (5) and (8), we get-
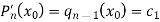
Hence the Newton-Raphson method simplifies to-
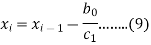
Example: Find all the roots of polynomial equation 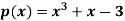 rounded off to three decimal places.
rounded off to three decimal places.
[Stop the iteration if |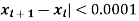
Sol.
The equation has three roots.
As there is only one change in the sign of the coefficient, by Descartes’ rule of sign the equation can have at most one positive real root.
The equation has no negative real roots since p(-x) = 0 has no change of sign of coefficients.
Here p(x) = 0 is of one degree, it has at least one real root.
So that the given equation has one positive real root and a complex pair.
Now let's find the real roots by Birge-Vieta method-
The initial iteration is-

So that-
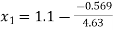 = 1.22289
= 1.22289
Similarly
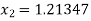
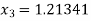
Here we see that 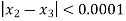 so that we stop the iteration.
so that we stop the iteration.
Hence the value of root is 1.213
Now we get the deflated polynomial of p(x).
In order to obtain a deflated polynomial, we need to find the quadratic equation by using the final approximation.[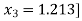

Here we notice p(1.213) = -0.0022,
That is, the magnitude of the error in satisfying p(x) = 0 is 0.0022.
We get-
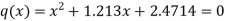
The roots of this quadratic equation are given by-[using quadratic equation]-
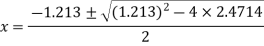
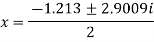
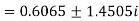
The three roots of the equation rounded off to three decimal places are 1.213, 0.6065+1.4505i and -0.6065 - 1.4505i
References:
[R1] J. B. Scarborough, “Numerical Mathematical Analysis”, Oxford & IBH, New Delhi.
[R2] Steven Chapra, Raymond P. Canale, “Numerical Methods for Engineers”, Tata McGraw Hill Publication.
[R3] S.S. Sastry, “Introductory Methods of Numerical Analysis”, PHI Learning Private Ltd.
[R4] P. Thangaraj, “Computer oriented Numerical Methods”, PHI Learning Private Ltd.
[R5] Yashwant Kanitkar, “Let us Python”, pbp publications
[R6] NPTEL course on Numerical Analysis, IIT, Roorkee.
[R7] NPTEL course on MATLAB Programming on Numerical Computation, IIT Madras
[R8] NPTEL course on Python for Data Science, IIT Madras
[R9] Jaan Kiusalaas, “Numerical Methods in Engineering with Python”, Cambridge University Press