Unit 6
Performance of Transmission Line
The transmission line has resistance R, inductance L, capacitance C and the shunt or leakage conductance G. These parameters along with the load and the transmission line determine the performance of the line.
Short Transmission Line
If the line is not more than 80 KV or if the voltage is not over than 66 KV then the line is known as the short transmission line. The capacitance of the line is governed by their length.
The effect of capacitance on the short transmission line is negligible, but for cable where the distance between the conductor is small, the effect of capacitance cannot be ignored.
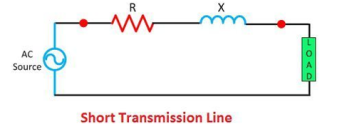
Figure1. Short transmission line
Medium Transmission Line
The line which is ranging from 80 to 240 km is termed as a medium transmission line. The capacitance of the medium transmission line cannot be ignored. The capacitance of the medium transmission line is lumped at one or more point of the lines.
The effect of the line is more at high frequency, and their leakages inductance and capacitance considered to be neglected. The medium transmission line is sub-divided into Pi – model and T – model.
Long Transmission Line
The line having a length more than 240 km is considered a long transmission line. All the four parameters (resistance, inductance, capacitance, and leakage conductance) are found to be equally distributed along the entire length of the line.
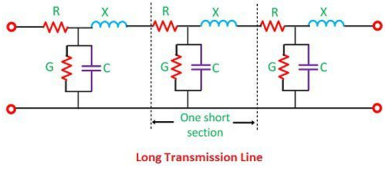
Figure2. Long transmission line
Key Takeaways:
The classification of the transmission lines depends on its voltage and the length of the conductor. The transmission line is the medium of transferring the power from the generating station to the load centre
The equivalent circuit of a short transmission line is shown in Figure where R and X represent the total resistance and inductive reactance of both the conductors that is go and return of a single- phase transmission line.
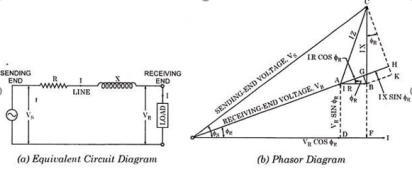
Figure3. Short transmission line
Fig (a) represent a 3-phase short transmission line if R and X represent the resistance and inductive reactance to neutral, I is the current in one conductor, VR is the receiving-end voltage to neutral, VS is the sending-end voltage to neutral, and the load is that in one phase; the voltage drop found in this way is the drop between a phase and neutral.
The Receiving-end voltage, VR = VS – I (R + j X) = VS – IZ … (1)
The quantity I Z is the voltage drop along the line.
In Fig. (b) phasor OI, OA AB, BC, AC and OC represent the load current I, receiving-end voltage VR, resistive drop I R in line, reactive drop I X in line, line impedance drop I Z and sending-end voltage VS respectively.
From phasor diagram shown in Fig. (b),
Sending-end voltage Vs = OC = √ OF 2 + FC 2
= √ (OD + DF) 2 + (FB +BC) 2
= √ (VR cos ɸ R + IR) 2 + ( VR sin ɸR + IX) 2 -------(2)
Sending end phase angle ɸs = tan -1 FC/OF = VR sin ɸR + IX / VR cos ɸR + IR ----(3)
And sending end power factor cos ɸs = OF/OC = VR cos ɸR + IR/ Vs
Key Takeaways:
A short transmission line is defined as a transmission line with an effective length less than 80 km (50 miles), or with a voltage less than 69 kV.
Nominal T Method
In Nominal T model of Transmission line, the whole shunt capacitance of line is assumed to be lumped at the middle of the line.
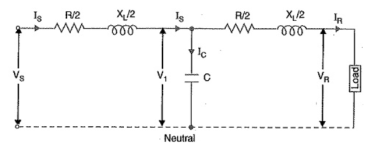
Figure 4. Nominal T
Let us now try to find the sending end voltage and current.
For that, we will apply kirchhof’s law.
Each parameter is shown in figure above with their meaning.
As the voltage across the shunt capacitance
V1 = (R/2 + jX/2)IR + VR ………(1)
Also, using Kirchhof’s current law,
Is = IR + Ic (phasor sum) ………………………….(2)
Therefore,
Vs = (R/2 + jX/2)Is + V1
= (R/2 + jX/2)IR + (R/2 + jX/2)Is + VR …………………….(3)
Let us now take the receiving end voltage as reference and assume that receiving end current or load current is lagging by some angle ØR.
Therefore,
VR = VR + j0
And IR = IR<-ØR = IR (CosØR – jSinØR)
As the current through the shunt capacitor lead by an angle 90° with respect to voltage across it i.e. V1, therefore
Ic = jωCV1
From equation (2),
Is = IR (CosØR – jSinØR) + jωCV1
= IR CosØR + j(ωCV1 – SinØR) ………………..(4)
Thus, by putting the value of V1 from equation (1) in equation (4), sending end current can be found.
Similarly, the sending end voltage can be calculated by putting the value of Is in equation (3). can also be calculated as we know the sending and receiving end voltage.
Nominal π Method
In Nominal π Method, the shunt capacitance of each line i.e. phase to neutral is divided into two equal parts. One part is lumped at the sending end while the other is lumped at receiving end as shown in figure below.
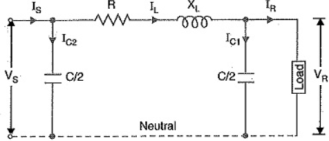
Figure 5. Nominal π method
In this method there is no effect of shunt capacitance at sending end on the line voltage drop and hence on voltage regulation but this accounts for the charging current in sending end.
Let
IR = Load Current per phase
R = Resistance per phase
X = Reactance per phase
C = Capacitance per phase
CosØR = Receiving end power factor (lagging)
Vs = Sending end voltage
Key Takeaways:
A transmission line having a length of more than 80 kms but less than 250 kms is considered as a medium transmission line.
Ferranti effect
The Ferranti effect is a phenomenon that describes the increase in voltage that occurs at the receiving end of a long transmission line relative to the voltage at the sending end.
The Ferranti effect is more prevalent when the load is small, or no load is connected that is an open circuit. The Ferranti effect can be stated as a factor, or as percent increase.
Representation of ‘T’ and ‘π’ models of lines as two port networks
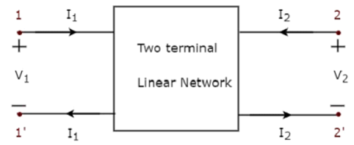
Figure 6: Two port network
Transmission parameters
A two-port network can be described by transmission parameters.
V1 = a11 V2 – a12 I2 ------------------------------------------(1)
I1 = a21 V2 – a22 I2 ------------------------------------------(2)
Where V2 and I 2 are independent variables and V1 and I1 are dependent variables. In matrix form, the above two equations can be rewritten as
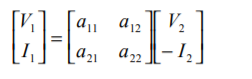
The transmission parameters can be found as
a11 = V1/V2 | I2 =0
a12 = -V1/I2 | V2=0
a21 = I1/V2 | I2=0
a22 = -I1/I2 | V2=0
The transmission parameters express the primary (sending end) variables V1 and I1 in terms of the secondary (receiving end) variables V2 and - I 2 .
The negative of I 2 is used to allow the current to enter the load at the receiving end.
Π Model
A two-port network can also be represented using y-parameters.
The describing equations are
I1 = y11 V1 + y12 V2 -------------------------------------------------------(1)
I2 = y21 V1 + y22 V2 ---------------------------------------------------------(2)
Where
V1 and V2 are independent variables
I1 and I2 are dependent variables
y 11= I1/V1 | V2 =0
y12= I1/V2 | V1=0
y21 = I2/V1 |V2=0
y22 = I2/V2| V1=0
The y-parameters are also called short-circuit admittance parameters. They are obtained as a ratio of current and voltage and the parameters are found by short-circuiting port 2 (V2 = 0) or port 1 (V1 = 0).
Find the y-parameters of the pi (π) network shown in Figure
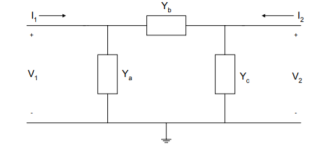
Figure7. Pi network
Using KCL, we have
I1 = V1 Ya + (V1 -V2) Yb = V1(Ya +Yb) – V2 Yb
I2 = V2 Yc + (V2-V1) Yb = -V1 Yb + V2(Yb + Yc)
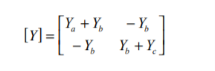
Key Takeaways:
In nominal 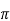 representation the lumped series impedance is placed in the middle while the shunt admittance is divided into two equal parts and placed at the two ends
representation the lumped series impedance is placed in the middle while the shunt admittance is divided into two equal parts and placed at the two ends
In any four- terminal network, the input voltage and input current can be expressed in terms of output voltage and output current.
The Circuit Constants of a Transmission Line is a 4-terminal network; two input terminals where power enters the network and two output terminals where power leaves the network.
Therefore, the input voltage (VS) and input current (IS) of a 3-phase Circuit Constants of a Transmission Line can be expressed as:
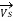 =
= 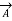
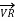 +
+ 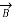
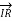
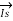 =
= 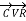 +
+ 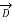
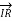
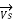 = sending end voltage per phase
= sending end voltage per phase
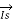 = sending end current
= sending end current
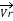 = receiving end voltage per phase
= receiving end voltage per phase
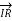 = receiving end current
= receiving end current
And A,B,C and D are the constants, known as generalised circuit constants of the transmission line.
Determination of Generalised Constants for Transmission Lines:
The sending end voltage (VS) and sending end current (IS) of a transmission line can be expressed as :
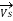 =
= 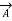
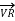 +
+ 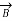
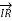 ------------------------(i)
------------------------(i)
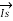 =
= 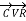 +
+ 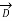
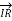 --------------------------(ii)
--------------------------(ii)
To determine the values of these constants for different types of transmission lines.
Short lines: In short transmission lines, the effect of line capacitance is neglected. Therefore, the line is considered to have series impedance. Shows the circuit of a 3-phase Circuit Constants of a Transmission Line on a single phase basis.
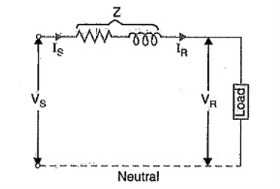
Figure8. Short lines
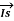 =
= 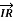 --------------------------(3)
--------------------------(3)
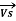 =
= 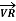 +
+ 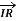
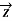 -----------------------------(4)
-----------------------------(4)
Comparing these with eqs, (i) and (ii), we have,
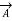 = 1;
= 1; 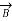 =
= 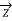 ,
, 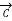 =0 and
=0 and 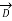 =1
=1
Incidentally 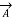 =
= 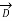
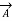
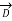 -
-  ,
,  = 1 x 1 -
= 1 x 1 -  x 0 =1
x 0 =1
(ii) Medium lines — Nominal T method. In this method, the whole line to neutral capacitance is assumed to be concentrated at the middle point of the line and half the line resistance and reactance are lumped on either side as shown in Figure.
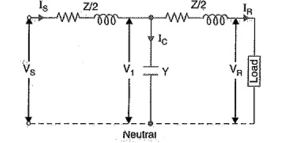
Figure 9. Nominal T method
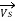 =
= 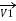 +
+ 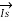
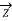 /2
/2
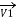 =
= 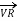 +
+ 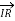
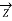 /2
/2
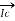 =
= 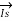 -
- 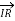 =
= 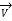
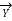 Y = shunt admittance
Y = shunt admittance
= 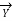 (
( 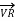 +
+ 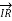
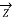 /2 )
/2 )
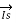 =
= 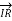 +
+ 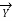
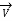 +
+ 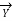
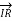
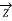 /2
/2
= 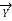
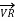 +
+ 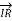
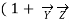 /2)
/2)
Substituting the value of V1 in we get,
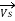 =
= 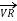 +
+ 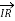
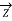 /2 +
/2 + 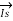
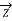 /2
/2
Substituting the value of IS, we get,
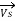 =
= 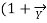
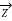
 2 )
2 ) 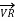 + (
+ ( 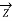 +
+ 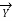
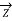 /4)
/4) 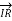
Comparing eqs.
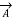 =
= 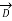 = 1 +
= 1 + 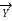
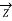 /2 ;
/2 ; 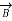 =
= 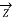 (1+
(1+ 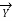
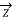 /4) ;
/4) ; 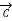 =
= 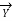
Key Takeaways:
Circuit Constants of a Transmission Line is a 4-terminal network ; two input terminals where power enters the network and two output terminals where power leaves the network.
Suppose the line is unloaded. In this case the receiving end voltage and sending end voltage will be same as there is no current flowing through the transmission line to cause voltage drop. But as soon as there is a flow of current, there will be a voltage drop. Thus, the voltage drop from no load to full load can be expressed as
Voltage drop = Receiving end voltage at no load – Receiving end voltage at full load = (Vs – VR)
This drop in voltage at receiving end when expressed as percentage of receiving end voltage VR is known as Voltage Regulation of Transmission Line.
% Voltage Regulation = [(Vs – VR) x100/ VR ] %
Transmission efficiency is a parameter which displays how much percentage of input power at sending end is delivered to the receiving end.
Then % transmission efficiency η = PRx100 / Ps %
But Ps = VsIsCosØs
And PR = VRIRCosØR
Where CosØs = Sending end power factor
And CosØR = Receiving end power factor
Hence,
% Transmission Efficiency
η= [VRIRCosØR / VsIsCosØs]x100%
If Ps is the input power at sending end, then only (Ps – Loss) will be available at the receiving end. Therefore (100 -η)% is the loss in transmission line resistance. This gives us a new method to calculate transmission efficiency.
If we know the loss in the line, then efficiency can be calculated as
% Efficiency η = [(Input Power – Loss) / Input Power]x100 %
= [(Ps – Loss) / Ps]x100 %
= [Ps/Ps – Loss/Ps]x100 %
= [1 – Loss/Ps]x100 %
If the resistance of line is R and current flowing through it is I then ohmic loss = I2R
So,
% Efficiency η = [1- I2R/Ps]
= [1- I2R / VsIsCosØs]
= [1- IR / VsCosØs] ..(since Is = I = current in transmission line)
Key Takeaways:
Regulation is defined as the change in voltage at the receiving or load end when the full-load is thrown off, the sending-end or supply voltage and supply frequency remaining unchanged.
References
1. Power System Engineering Book by D.P. Kothari and I.J. Nagrath
2. Power System Analysis and Design Book by J. Duncan Glover and Mulukutla S Sarma
3. A Course In Power Systems Book by J. B. Gupta
4. Modern Power System Analysis Book by D.P. Kothari and I.J. Nagrath
5. Electrical Power Systems Book by Murty P.S.R
6. Elements of Power System Analysis Book by William D. Stevenson