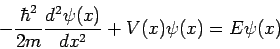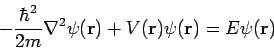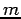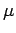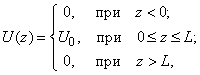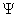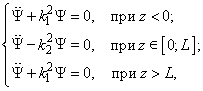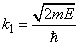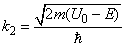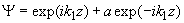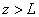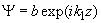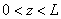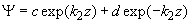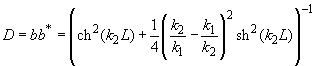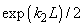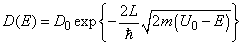Unit - 3
Quantum mechanics
According to de-Broglie hypothesis, the energy of the universe is in the form of matter and radiation. So, both matter and radiation should have similar properties.
But radiation shows dual nature sometimes as wave and sometimes as particle. So, matter should have wave which can be expressed as:
Matter wave length = h/mv
where m is mass of particles/ matter
v= velocity and h is plank’s constant
Derivation of de-Broglie’s wavelength:
According to Plank’s quantum theory, energy of photon is expressed as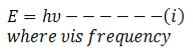
According to Einstein’s mass energy relation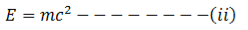
Now from equation i and ii we get
This equation shows that wavelength depends upon mass and velocity of light that is momentum of the particle.
If the particle of a mass m moves with velocity v then the matter wavelength can be expressed as which is known as de-Broglie wavelength.
Hence the de-Broglie wavelength ranges between 0 and infinity.
Phase and group velocity are two important and related concepts in wave mechanics. They arise in quantum mechanics in the time development of the state function for the continuous case that is wave packets.
Harmonic Waves and Phase Velocity
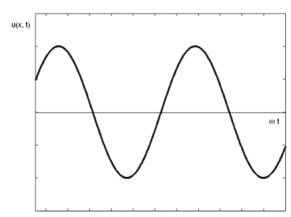
A one-dimensional harmonic wave as shown in figure 1 is described by the equation,

where A0 is the wave amplitude,
w is the circular frequency;
k is the wave number;
and 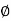 is an initial, constant phase.
is an initial, constant phase.
Sometimes the wave number is referred to as the spatial frequency or propagation constant.
|
Figure 1: Harmonic Wave
This is a monochromatic wave of one frequency. There are no strictly monochromatic waves in nature.
For example, the generating source of the wave may move slightly, introducing spurious frequencies.
In general, these waves propagate without warping. That is, the phase  (x, t) is a constant:
(x, t) is a constant:
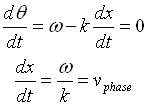
vphase is the phase velocity for a wave.
- For sending information, these waves are not useful because they are the same throughout time and space. Some must be modulated, such as frequency or amplitude, in order to convey information.
- The resulting wave may be a perturbation that acts over a short distance, that is a wave packet. This wave packet can be considered to be a superposition of a number of harmonic waves, that is in other words a Fourier series or integral.
Group Velocity
In order to convey information, it is essential to have a thing more than a simple harmonic wave is required. However, the superposition of many such waves of varying frequencies can result in an "envelope" wave and a carrier wave within the envelope.
The envelope can transmit data.
A simple example is the superposition of two harmonic waves with frequencies that are very close (w1 ~w2) and of the same amplitude. The equations for the motion are,
|
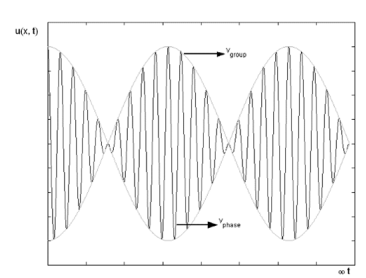
The plot of such a wave is shown in Figure 2.
|
Figure 2: Group Velocity
The envelope (the green line) is given by u1 and travels at the group velocity. The carrier wave (the blue line) travels at the phase velocity and is given by u2. The wave packet moves at the group velocity. It is the envelope which carries information. Group velocity is given by,
|
Phase and group velocity are related through Rayleigh's formula,
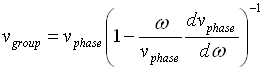
If the derivative term is zero, group velocity equals phase velocity.
In this case, there is no dispersion.
Dispersion is when the distinct phase velocities of the components of the envelope cause the wave packet to "spread out" over time.
- The observables have only discrete sets of experimental values. For example, the values of the energy of a bound system are always discrete, and angular momentum components have values that take the form mℏ, where m is either an integer or a half-integer, positive or negative.
- The position of a particle or the linear momentum of a free particle can take continuous values in both quantum and classical theory. The mathematics of observables with a continuous spectrum of measured values is somewhat more complicated than for the discrete case but presents no problems of principle.
- An observable with a continuous spectrum of measured values has an infinite number of state functions. The state function Ψ of the system is regarded as a combination of the state functions of the observable, but the sum has to be replaced by an integral.
- The uncertainty principle is significant only on the atomic scale because of the small value of h in everyday units.
- If the position of a macroscopic object with a mass of, say, one gram is measured with a precision of 10−6 metre, the uncertainty principle states that its velocity cannot be measured to better than about 10−25 metre per second.
- However, if an electron is located in an atom about 10−10 metre across, the principle gives a minimum uncertainty in the velocity of about 106 metre per second.
- Wave function is a variable quantity that mathematically describes the wave characteristics of a particle.
- The value of the wave function of a particle at a given point of space and time is related to the likelihood of the particle being there at the time.
- By analogy with waves such as those of sound, a wave function, designated by the Greek letter psi, Ψ, may be thought of as an expression for the amplitude of the particle wave.
- The square of the wave function, Ψ2, however, does have physical significance: the probability of finding the particle described by a specific wave function Ψ at a given point and time is proportional to the value of Ψ2.
Time-Dependent Schrödinger Equation
The time-dependent Schrödinger equation cannot be derived using elementary methods and is generally given as a postulate of quantum mechanics. The single-particle three-dimensional time-dependent Schrödinger equation is
where Of course, the time-dependent equation can be used to derive the time-independent equation. If we write the wavefunction as a product of spatial and temporal terms,
or
Since the left-hand side is a function of If we tentatively designate this constant
and The latter equation is once again the time-independent Schrödinger equation. Theformer equation is easily solved to yield
The Hamiltonian in equation (5) is a Hermitian operator, and the eigenvalues of a Hermitian operator must be real, so (recall Euler's formula Thus if then the total wave function There are some interesting consequences of this. First of all, the quantity
Secondly, the expectation value for any time-independent operator is also time-independent, if
For these reasons, wave functions of the form (7) are called stationary states. The state Equation (7) represents a particular solution to equation (1). The general solution to equation (1) will be a linear combination of these particular solutions, that is
|
The Time-Independent Schrödinger Equation The one-dimensional classical wave equation, By introducing the separation of variables
we obtain
If we introduce one of the standard wave equation solutions for
Now we have an ordinary differential equation describing the spatial amplitude of the matter wave as a function of position. The energy of a particle is the sum of kinetic and potential parts
which can be solved for the momentum,
Now we can use the de Broglie formula to get an expression for the wavelength
The term
When this result is substituted into equation (4) we obtain the famous time-independent Schrödinger equation
which is almost always written in the form
This single-particle one-dimensional equation can easily be extended to the case of three dimensions, where it becomes
A two-body problem can also be treated by this equation if the mass
|
|
3.6 Application of Schrodinger equation:
|
- In classical mechanics, to describe a system of material point at a certain moment of time, it is enough to set every point coordinates and momentum components.
- Using the principle of quantum mechanics, itis impossible to determine simultaneously coordinates and momentum components of even single point according to the He-isenberg uncertainty principle.
- In order to describe the system completely, an associated complex function is introduced in quantum mechanics.
- The wavefunction
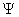 , a function of time and all system particles position, is a solution of the wave Schrodinger equation.
, a function of time and all system particles position, is a solution of the wave Schrodinger equation. - In order to use the system wavefunction, one should determine
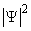 rather than
rather than  . Then, the probability for finding particles in an elementary volume dxdydz is given by
. Then, the probability for finding particles in an elementary volume dxdydz is given by 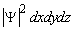 .
.
Let’s calculate the transparency of the rectangular barrier [1, 2]. Suppose that electrons of potential energy
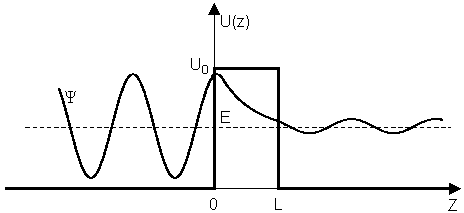
(1) impinge on the rectangular potential barrier and the total energy E is less than U0 (Fig. 1).
Fig.3. Rectangular potential barrier and particle wave function The stationary Schrodinger equations can be written as follows
(2) where The solution to the wave equation at A general solution inside the potential barrier The barrier transmission coefficient can be naturally considered as a ratio of the transmitted electrons probability flux density to that one of the incident electrons. In the case under consideration this ratio is just equal to the squared wavefunction module at
(3) If
(4) where Thus, analytical calculation of the rectangular barrier transmission coefficient is rather a simple task. |
Tunneling effect examples
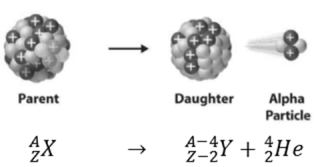
- Alpha decay
Alpha decay represents the disintegration of a parent nucleus to a daughter through the emission of the nucleus of a helium atom. This transition can be characterized as:
|
Figure 4. Alpha Decay
As can be seen from the figure, alpha particle is emitted in alpha decay.Among the variety of channels in which a nucleus decays, alpha decay has been one of the most studied.
The alpha decay channel in heavy and super heavy nuclei which provide information on the fundamental properties of nuclei far from stability, such as their ground state energies and the structure of their nuclear levels.
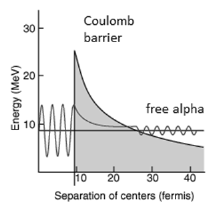
Alpha decay is a quantum tunnelling process. In order to be emitted, the alpha particle must penetrate a potential barrier. This is similar to cluster decay, in which an atomic nucleus emits a small “cluster” of neutrons and protons (e.g. 12C).
|
.
Fig 5. Graph
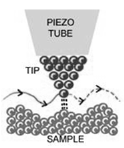
A scanning tunnelling microscope (STM) is a non-optical microscope that works by scanning an electrical probe tip over the surface of a sample at a constant spacing.
STM
The STM sample must conduct electricity for the process to work. The STM uses a tip that ends in a single atom, and a voltage is passed through the tip and the sample.
Electrons use a quantum mechanical effect to ‘tunnel’ from the tip to the sample and vice versa. The current that results depends upon the distance between the probe tip and the sample surface.
The tip is attached to a piezoelectric tube, and the voltage applied to the piezo rod is altered to maintain a constant distance of the tip from the surface. The changes in this voltage allow a three-dimensional picture of the material surface to be built up as the tip is scanned back and forth across the sample.
|
Figure6. STM tip
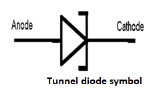
- Tunnel diode
A Tunnel diode is a heavily doped p-n junction diode in which the electric current decreases as the voltage increases.
In tunnel diode, electric current is caused by “Tunnelling”. The tunnel diode is used as a fast switching device in computers. It is also used in high-frequency oscillators and amplifiers.
- In tunnel diode, the p-type semiconductor act as an anode and the n-type semiconductor act as a cathode.
|
Figure 7. Tunnel doide
- The anode is a positively charged electrode which attracts electrons whereas cathode is a negatively charged electrode which emits electrons.
- In tunnel diode, n-type semiconductor emits or produces electrons so it is referred to as the cathode.
- On the other hand, p-type semiconductor attracts electrons emitted from the n-type semiconductor so p-type semiconductor is referred to as the anode.
Construction:
- If a semiconductor diode is heavily doped with impurities, it will exhibit negative resistance. Negative resistance means the current across the tunnel diode decreases when the voltage increases.
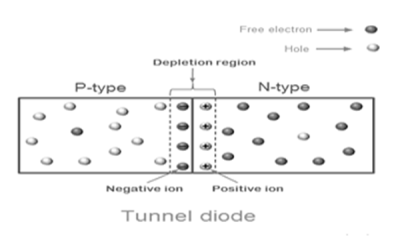
- The operation of tunnel diode depends on the quantum mechanics principle known as “Tunnelling”.
- In electronics, tunnelling means a direct flow of electrons across the small depletion region from n-side conduction band to the p-side valence band.
|
Fig 8. PN junction
The germanium material is commonly used to make the tunnel diodes. They are also made from other types of materials such as gallium arsenide, gallium antimonide, and silicon.
- Computers are getting smaller and faster day by day because electronic components are getting smaller and smaller. However, this process may meet its physical limit.
- Electricity is flow of electrons. Since size of transistors is shrinking to size of few atoms, transistors cannot be used as switch because electron may transfer themselves to the other side of blocked passage by the process called quantum tunnelling.
- Quantum mechanics is a branch of physics that explores physical world at most fundamental level.
- At this level particle behave differently from classical world taking more than one state at the same time and interacting with other particles that are very far away. Phenomena like superposition and entanglement take place.
- Quantum computers can easily crack the encryption algorithms used today in very less time. They have great solving optimization problems.
Reference:
1. Engineering Physics-Avadhanulu, Kshirsagar, S. Chand Publications
2. A textbook of optics- N Subrahmanyam and BriLal , S. Chand Publications
3. Engineering Physics- Gaur, Gupta, Dhanpat Rai and Sons Publications
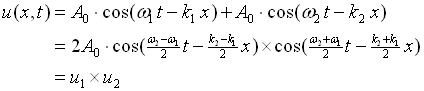
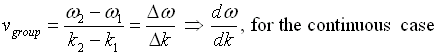
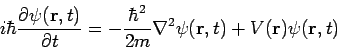
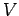

![\begin{displaymath}
\psi({\bf r}) i \hbar \frac{df(t)}{dt} = f(t) \left[
- \frac{\hbar^2}{2m} \nabla^2 + V({\bf r}) \right] \psi({\bf r})
\end{displaymath}](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1642900519_4760308.png)
![\begin{displaymath}
\frac{i \hbar}{f(t)} \frac{df}{dt} = \frac{1}{\psi({\bf r})}...
...frac{\hbar^2}{2m} \nabla^2 + V({\bf r}) \right] \psi({\bf r})
\end{displaymath}](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1642900519_5178401.png)
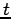
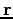
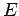
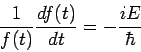
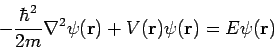
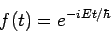
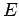

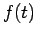
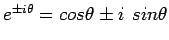
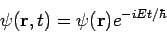
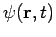
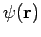
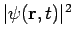
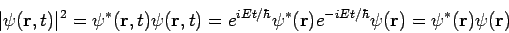
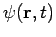
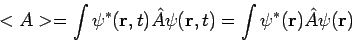
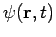
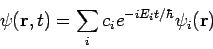
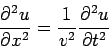
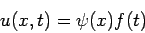
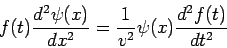
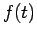
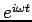
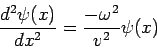


![\begin{displaymath}
p = \{ 2m [ E - V(x) ] \} ^{1/2}
\end{displaymath}](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1642900521_1756594.png)
![\begin{displaymath}
\lambda = \frac{h}{p} = \frac{h}{\{ 2m [ E - V(x) ] \}^{1/2}}
\end{displaymath}](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1642900521_2164383.png)
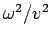

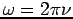
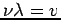
![\begin{displaymath}
\frac{\omega^2}{v^2} = \frac{4 \pi^2 \nu^2}{v^2} =
\frac{4\pi^2}{\lambda^2} = \frac{2m[E - V(x)]}{\hbar^2}
\end{displaymath}](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1642900521_5254667.png)
![\begin{displaymath}
\frac{d^2\psi(x)}{dx^2} + \frac{2m}{\hbar^2} [ E - V(x)]\psi(x) = 0
\end{displaymath}](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1642900521_5881822.png)