MICRO
Unit - 3Microwave Network Analysis 3.1 Introduction and Applications of Impedance and Equivalent Voltages and CurrentsAt low frequency, the circuits can be analysed with the help of Kirchhoff’s law. At low frequencies, the circuit is assumed as an inter-connection of lumped components and the other important parameters like phase delay, propagation constant and EM wave modes are generally not taken into consideration. But at higher frequencies, the basic theory of circuit analysis can’t be applied directly to the circuits because circuit is made up of distributed components. Instead of circuit analysis, field analysis is used to analyse the microwave circuits. In this unit, we deal with important network parameters and their application in analysing the microwave circuits and passive components. TWO PORT NETWORK:Linear two port network can be defined by a number of equivalent circuit parameters like transfer matrix, impedance matrix, admittance matrix and scattering matrix. A typical two port network is shown in the figure, Transfer Matrix or the Transmission Matrix (ABCD)The transfer matrix also known as ABCD matrix relates the voltage and current at port 1 to those at port 2. In equation form; V1 = AV2 + BI2 and
Transfer Matrix or the Transmission Matrix (ABCD)The transfer matrix also known as ABCD matrix relates the voltage and current at port 1 to those at port 2. In equation form; V1 = AV2 + BI2 and  I1 = CV2 + DI2
I1 = CV2 + DI2 In matrix form
In matrix form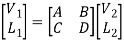 whereT = Transfer Matrix =
whereT = Transfer Matrix = 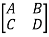 3.2 Impedance and Admittance MatricesThe impedance matrix relates the two voltages V1 and V2 to the two currents I1 and I2.In equation form; V1 = Z11I1– Z12I2and V2 = Z21 I1 – Z22 I2In matrix form,
3.2 Impedance and Admittance MatricesThe impedance matrix relates the two voltages V1 and V2 to the two currents I1 and I2.In equation form; V1 = Z11I1– Z12I2and V2 = Z21 I1 – Z22 I2In matrix form,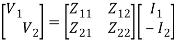 where,Z = impedance matrix =
where,Z = impedance matrix = 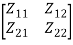 Admittance Matrix The admittance matrix (Y) is the inverse of impedance matrix. Mathematically; Y = Z-1 3.3 The Transmission (ABCD) MatrixThe scattering matrix relates the outgoing waves b1, b2 to the incident waves a1 and a2 (as shown in the first figure ) that are incident on port 1 and port 2 respectively. In equation form; b1 = S11a1 + S12 a2and b2 = S21 a1 + S22a2 In matrix form,
Admittance Matrix The admittance matrix (Y) is the inverse of impedance matrix. Mathematically; Y = Z-1 3.3 The Transmission (ABCD) MatrixThe scattering matrix relates the outgoing waves b1, b2 to the incident waves a1 and a2 (as shown in the first figure ) that are incident on port 1 and port 2 respectively. In equation form; b1 = S11a1 + S12 a2and b2 = S21 a1 + S22a2 In matrix form,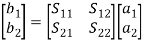 where, S = scattering matrix =
where, S = scattering matrix = 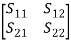 3.4 Scattering Matrix: SignificanceOne method of describing the behaviour of a network at microwave frequencies is in terms of scattering parameters which are commonly referred to as S parameters.Scattering is a general term that refers to transmitting in all directions and reflecting back to the source. The derivation of S parameters is based on forward and backward travelling waves on terminal transmission lines. That’s why they are most commonly used in microwave engineering. The forward and backward travelling waves are also referred to as incident and reflected waves, respectively. The S parameters are defined using the amplitudes of incident waves (i.e. voltage waves entering the ports) and reflected waves (i.e. voltage waves leaving the ports). Scattering matrix: The directly measurable quantities at high frequencies are amplitudes and phase angles of reflected waves (or scattered waves). The scattered wave amplitudes are linearly related to the incident wave amplitudes. The matrix describing the relationship between the voltage waves incident at the ports and those reflected from the ports is called a scattering matrix or an S matrix. Normalized incident and reflected voltage waves (ai and bi): The incident wave is defined as that component which would exist if the port under consideration were conjugately matched to the normalizing impedance at that port. Therefore, S parameters describe the interrelationships of a new set of variables, ai and bi. The variables ai and bi are defined in terms of the terminal current Ii, terminal voltage Vi and arbitrary reference impedance Zi. They are the normalized complex voltage waves which are incident on and reflected from the ith port of the network. The Z, Y, h, ABCD, and scattering parameters are introduced in this chapter to characterize the low- and high-frequency circuits, respectively. Scattering matrix calculations are also presented for one-port, two-port (isolator, gyrator, attenuator, etc), three-port (circulator, E-plane and H-plane Tees), and four-port (directional coupler, rat race, and Magic Tee) junction devices. 3.5 Formulation and Properties: S-Matrix Calculations for-2 Port Network JunctionS parameters play a major role in network analysis at microwave frequencies. It is difficult to get the required short and open circuit tests for higher frequencies by using the Z, Y, h, and ABCD parameters at higher frequencies. Thus, the S parameters gained importance at higher frequencies. In order to use Z, Y, h, and ABCD parameters at high frequency, let us suppose we short the circuit with a wire; the wire itself possesses an inductance that is of large magnitude. Likewise for open circuit, capacitive loading at the terminal will be of large magnitude.In microwave engineering, multiport networks are characterized using scattering matrices at high frequencies. They are used to represent microwave devices, such as isolators, circulators, directional couplers, amplifiers, E planes, H planes, Magic Tees, and hybrid rings and are easily related to concepts of gain, loss, and reflection. FORMULATION OF S MATRIXLinear networks can be completely characterized by parameters that are measured at the network ports without knowing the content of the networks. Networks can have any number of ports. An analysis of a 2-port network is taken into consideration to explain the theory. At each port i, an entering voltage and current waves are defined as Vi+ and Ii+ and the leaving voltage and a current waves are defined as Vi- and Ii- (as shown in the figure). These voltage and current waves are defined in such a way that the voltage is proportional to the transverse electric field and current is proportional to the magnetic fields of the wave.
3.4 Scattering Matrix: SignificanceOne method of describing the behaviour of a network at microwave frequencies is in terms of scattering parameters which are commonly referred to as S parameters.Scattering is a general term that refers to transmitting in all directions and reflecting back to the source. The derivation of S parameters is based on forward and backward travelling waves on terminal transmission lines. That’s why they are most commonly used in microwave engineering. The forward and backward travelling waves are also referred to as incident and reflected waves, respectively. The S parameters are defined using the amplitudes of incident waves (i.e. voltage waves entering the ports) and reflected waves (i.e. voltage waves leaving the ports). Scattering matrix: The directly measurable quantities at high frequencies are amplitudes and phase angles of reflected waves (or scattered waves). The scattered wave amplitudes are linearly related to the incident wave amplitudes. The matrix describing the relationship between the voltage waves incident at the ports and those reflected from the ports is called a scattering matrix or an S matrix. Normalized incident and reflected voltage waves (ai and bi): The incident wave is defined as that component which would exist if the port under consideration were conjugately matched to the normalizing impedance at that port. Therefore, S parameters describe the interrelationships of a new set of variables, ai and bi. The variables ai and bi are defined in terms of the terminal current Ii, terminal voltage Vi and arbitrary reference impedance Zi. They are the normalized complex voltage waves which are incident on and reflected from the ith port of the network. The Z, Y, h, ABCD, and scattering parameters are introduced in this chapter to characterize the low- and high-frequency circuits, respectively. Scattering matrix calculations are also presented for one-port, two-port (isolator, gyrator, attenuator, etc), three-port (circulator, E-plane and H-plane Tees), and four-port (directional coupler, rat race, and Magic Tee) junction devices. 3.5 Formulation and Properties: S-Matrix Calculations for-2 Port Network JunctionS parameters play a major role in network analysis at microwave frequencies. It is difficult to get the required short and open circuit tests for higher frequencies by using the Z, Y, h, and ABCD parameters at higher frequencies. Thus, the S parameters gained importance at higher frequencies. In order to use Z, Y, h, and ABCD parameters at high frequency, let us suppose we short the circuit with a wire; the wire itself possesses an inductance that is of large magnitude. Likewise for open circuit, capacitive loading at the terminal will be of large magnitude.In microwave engineering, multiport networks are characterized using scattering matrices at high frequencies. They are used to represent microwave devices, such as isolators, circulators, directional couplers, amplifiers, E planes, H planes, Magic Tees, and hybrid rings and are easily related to concepts of gain, loss, and reflection. FORMULATION OF S MATRIXLinear networks can be completely characterized by parameters that are measured at the network ports without knowing the content of the networks. Networks can have any number of ports. An analysis of a 2-port network is taken into consideration to explain the theory. At each port i, an entering voltage and current waves are defined as Vi+ and Ii+ and the leaving voltage and a current waves are defined as Vi- and Ii- (as shown in the figure). These voltage and current waves are defined in such a way that the voltage is proportional to the transverse electric field and current is proportional to the magnetic fields of the wave.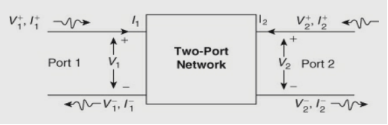 Vi+, Ii+, Vi-, and Ii- are the complex amplitudes of sinusoidal excitations. The power of the entering or leaving wave is given by the product of the voltage and current. The characteristic impedance (Z0) of the port is given by the ratio of the voltage and current. The total voltage and the total current at port i are as follows:
Vi+, Ii+, Vi-, and Ii- are the complex amplitudes of sinusoidal excitations. The power of the entering or leaving wave is given by the product of the voltage and current. The characteristic impedance (Z0) of the port is given by the ratio of the voltage and current. The total voltage and the total current at port i are as follows: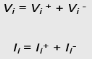 When a voltage wave (Vi+) is incident at one port, some fraction of the signal bounces back out of that port, some of it scatters and exits from other ports, and some of it disappears as heat or electromagnetic radiation. Usually, all the microwave network ports have similar connectors (coaxial connectors or waveguide flanges) with an impedance of 50 Ω, and the characteristic impedances (Z0) of the ports have a similar value. However, in a general case, the characteristic impedances (Z0) may have different values. For example, the ports of a coaxial-to-waveguide adapter have different characteristic impedances. Then, the voltage waves should be normalized. S-PARAMETER REPRESENTATION OF A 2 - PORT NETWORKThe behaviour of the network in terms of the injected and reflected power waves can be described by a set of linear equations. For the 2-port case, the outputs can be related to the inputs by,b1 = S11a1 + S12a2b2 = S21a1 + S22a2where b1 is the wave travelling away from port 1 (i.e. toward source) = wave incident on port 1 times the reflection coefficient (S11a1) + wave incident on port 2 times transmission coefficient from port 2 to port 1 (S12a2). Similarly, b2 is the wave traveling away from port 2 = S21a1 + S22a2. From the above equations, we can say that each signal coming out of a two-port network (i.e. b1 or b2) will have two components: some signal reflected from the same port and some signal transferred from the other port. We can interpret Sij as the power measured at port i due to the incident power at port j. The term Sij can be computed directly by the following formula:
When a voltage wave (Vi+) is incident at one port, some fraction of the signal bounces back out of that port, some of it scatters and exits from other ports, and some of it disappears as heat or electromagnetic radiation. Usually, all the microwave network ports have similar connectors (coaxial connectors or waveguide flanges) with an impedance of 50 Ω, and the characteristic impedances (Z0) of the ports have a similar value. However, in a general case, the characteristic impedances (Z0) may have different values. For example, the ports of a coaxial-to-waveguide adapter have different characteristic impedances. Then, the voltage waves should be normalized. S-PARAMETER REPRESENTATION OF A 2 - PORT NETWORKThe behaviour of the network in terms of the injected and reflected power waves can be described by a set of linear equations. For the 2-port case, the outputs can be related to the inputs by,b1 = S11a1 + S12a2b2 = S21a1 + S22a2where b1 is the wave travelling away from port 1 (i.e. toward source) = wave incident on port 1 times the reflection coefficient (S11a1) + wave incident on port 2 times transmission coefficient from port 2 to port 1 (S12a2). Similarly, b2 is the wave traveling away from port 2 = S21a1 + S22a2. From the above equations, we can say that each signal coming out of a two-port network (i.e. b1 or b2) will have two components: some signal reflected from the same port and some signal transferred from the other port. We can interpret Sij as the power measured at port i due to the incident power at port j. The term Sij can be computed directly by the following formula: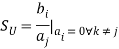 where k is 1 to n (here, k = 1 or 2) Here, n represents the number of ports. In matrix form, the above equations can be written as,
where k is 1 to n (here, k = 1 or 2) Here, n represents the number of ports. In matrix form, the above equations can be written as, The outgoing waves are expressed in terms of the incoming waves by the matrix equation [b] = [S] [a] where S is an n × n square matrix of complex numbers called the scattering matrix
The outgoing waves are expressed in terms of the incoming waves by the matrix equation [b] = [S] [a] where S is an n × n square matrix of complex numbers called the scattering matrix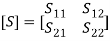 The behavior of the network is determined by the S matrix ([S]) and all the elements of this matrix are called S parameters. They are frequency dependent. S parameters for two-port networks are given as follows:
The behavior of the network is determined by the S matrix ([S]) and all the elements of this matrix are called S parameters. They are frequency dependent. S parameters for two-port networks are given as follows: 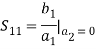
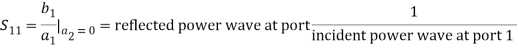


 S-PARAMETER EVALUATIONS parameters can only be determined under conditions of perfect matching at the input or output port.Determination of S11, S21 parameters: S11, S21 parameters can be computed if port 2 is terminated with a matched load (Z0). Then, the incident wave applied at port 2 (i.e. a2) becomes zero (a2 = 0), and the wave leaving port 2 (i.e. b2) is presented (see figure). The b2 is the wave travelling away from port 2 and is due to the wave incident at port 1 (i.e. a1) times the transmission factor (S21) from port 1 to port 2. Similarly, b1 is the wave travelling away from port 1 toward the source and is equivalent to the wave incident at port 1 (i.e. a1) times the reflection coefficient (S11).
S-PARAMETER EVALUATIONS parameters can only be determined under conditions of perfect matching at the input or output port.Determination of S11, S21 parameters: S11, S21 parameters can be computed if port 2 is terminated with a matched load (Z0). Then, the incident wave applied at port 2 (i.e. a2) becomes zero (a2 = 0), and the wave leaving port 2 (i.e. b2) is presented (see figure). The b2 is the wave travelling away from port 2 and is due to the wave incident at port 1 (i.e. a1) times the transmission factor (S21) from port 1 to port 2. Similarly, b1 is the wave travelling away from port 1 toward the source and is equivalent to the wave incident at port 1 (i.e. a1) times the reflection coefficient (S11).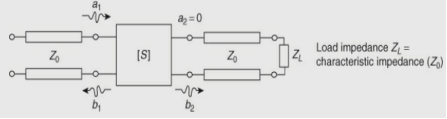
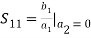 ,
, 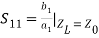 By defining Zin as the input impedance given by ZL = Z0i.e;
By defining Zin as the input impedance given by ZL = Z0i.e;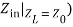 we have,
we have,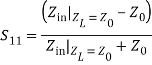 From the above equation, we can say that the reflection coefficient (S11) is the method of specifying the input impedance Zin.S11 = b1/a1 that is, the input reflection coefficient (when a2 = 0) S21 = b2/a1 that is, the forward transmission gain/loss (when a2 = 0) Determination of S22, S12 parameters: S22, S12 parameters can be computed, if port 1 is terminated with a matched load (Z0). Then, the incident wave at port 1 (i.e. a1) becomes zero (a1 = 0), and the wave leaving port 1 (i.e. b1) is presented (see figure). The b1 is the wave travelling away from port 1 and is due to the wave incident at port 2 (i.e. a2) times the transmission factor (S12) from port 2 to port 1. Similarly, b2 is the wave travelling away from port 2 toward the source and is due to the wave incident at port 2 (i.e. a2) times the reflection coefficient (S22).
From the above equation, we can say that the reflection coefficient (S11) is the method of specifying the input impedance Zin.S11 = b1/a1 that is, the input reflection coefficient (when a2 = 0) S21 = b2/a1 that is, the forward transmission gain/loss (when a2 = 0) Determination of S22, S12 parameters: S22, S12 parameters can be computed, if port 1 is terminated with a matched load (Z0). Then, the incident wave at port 1 (i.e. a1) becomes zero (a1 = 0), and the wave leaving port 1 (i.e. b1) is presented (see figure). The b1 is the wave travelling away from port 1 and is due to the wave incident at port 2 (i.e. a2) times the transmission factor (S12) from port 2 to port 1. Similarly, b2 is the wave travelling away from port 2 toward the source and is due to the wave incident at port 2 (i.e. a2) times the reflection coefficient (S22). Mathematically, the above statements can be written, as the same analysis and comments clearly apply to S22.By symmetry,
Mathematically, the above statements can be written, as the same analysis and comments clearly apply to S22.By symmetry,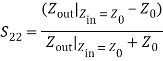 From the above equation, we can say that the reflection coefficient (S22) is the method of specifying the output impedance Z0:S22 = b2/a2; that is, the output reflection coefficient (when a1 = 0) S12 = b1/a2; that is, the reverse transmission gain/loss (when a1 = 0)a1 and b1 are rms voltages normalized by √Z0 and S22 are the reflection coefficients with the opposite port terminated at Z0. S21 and S12are the forward and reverse transducer gains, respectively. S Parameters for 3 PortsA 3-port network is shown in the figure. The matrix equations for a 3-port network are as follows: b1 = S11a1 + S12a2 + S13a3b2 = S21a1 + S22a2 + S23a3b3 = S31a1 + S32a2 + S33a3 In matrix form,
From the above equation, we can say that the reflection coefficient (S22) is the method of specifying the output impedance Z0:S22 = b2/a2; that is, the output reflection coefficient (when a1 = 0) S12 = b1/a2; that is, the reverse transmission gain/loss (when a1 = 0)a1 and b1 are rms voltages normalized by √Z0 and S22 are the reflection coefficients with the opposite port terminated at Z0. S21 and S12are the forward and reverse transducer gains, respectively. S Parameters for 3 PortsA 3-port network is shown in the figure. The matrix equations for a 3-port network are as follows: b1 = S11a1 + S12a2 + S13a3b2 = S21a1 + S22a2 + S23a3b3 = S31a1 + S32a2 + S33a3 In matrix form,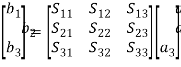
 PROPERTIES OF A SCATTERING MATRIXProperties of the S matrix for an n-port network are as follows: Scattering matrix [S ] is always the square matrix of the order n × n. Under perfect matched conditions, diagonal elements of [S] are equal to “0”. i.e. Sii = 0 [S] is symmetric for all reciprocal networks, that is, [S] = [S]T where [S]T is the transpose of [S]. In other words, [S]is symmetric about the main diagonal. i.e Sij = SjiIf a device (or network) is lossless, then the S matrix is unitary [S] [S]* = [I ] where [S]* is the complex conjugate of S. [I ] is the unit matrix defined as,
PROPERTIES OF A SCATTERING MATRIXProperties of the S matrix for an n-port network are as follows: Scattering matrix [S ] is always the square matrix of the order n × n. Under perfect matched conditions, diagonal elements of [S] are equal to “0”. i.e. Sii = 0 [S] is symmetric for all reciprocal networks, that is, [S] = [S]T where [S]T is the transpose of [S]. In other words, [S]is symmetric about the main diagonal. i.e Sij = SjiIf a device (or network) is lossless, then the S matrix is unitary [S] [S]* = [I ] where [S]* is the complex conjugate of S. [I ] is the unit matrix defined as,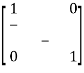 Examples of S Matrices1-port S matrixConsider 1-Port as simple lumped elements and cavities with one test port, long transmission lines or antennas. 1-port S-matrix is a matrix consisting of a single element, and the single element is the scattering parameter or reflection coefficient. It can be a 1×1 matrix; one row and one column.1-port is characterized by their reflection coefficient (Γ), or in terms of S parameters, S11.Ideal short for 1-port is given by S11 = −1 Ideal termination is given by S11 = 0 Active termination or reflection amplifier is given by |S11| > 1 2-port S MatrixAn isolator is a 2-port device. Both the ports are perfectly matched to the junction, that is, the diagonal elements are zero. Sii = 0, that is, S11 = S22 = 0, and the junction is non reciprocal (Sij ≠ Sji). Hence, if the source is at port (1), its purpose is to prevent the reflected wave from port (2), that is, S12 = 0The S matrix for an ideal isolator is,
Examples of S Matrices1-port S matrixConsider 1-Port as simple lumped elements and cavities with one test port, long transmission lines or antennas. 1-port S-matrix is a matrix consisting of a single element, and the single element is the scattering parameter or reflection coefficient. It can be a 1×1 matrix; one row and one column.1-port is characterized by their reflection coefficient (Γ), or in terms of S parameters, S11.Ideal short for 1-port is given by S11 = −1 Ideal termination is given by S11 = 0 Active termination or reflection amplifier is given by |S11| > 1 2-port S MatrixAn isolator is a 2-port device. Both the ports are perfectly matched to the junction, that is, the diagonal elements are zero. Sii = 0, that is, S11 = S22 = 0, and the junction is non reciprocal (Sij ≠ Sji). Hence, if the source is at port (1), its purpose is to prevent the reflected wave from port (2), that is, S12 = 0The S matrix for an ideal isolator is,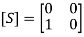 3-port S matrixFor a 3-port circulator, all the three ports are perfectly matched to the junction.
3-port S matrixFor a 3-port circulator, all the three ports are perfectly matched to the junction.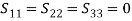 and the junction is non reciprocal (Sij ≠ Sji),
and the junction is non reciprocal (Sij ≠ Sji), 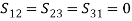 Hence, for a 3-port circulator, a 3 × 3 S matrix is given by,
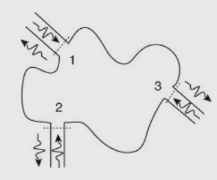
Hence, for a 3-port circulator, a 3 × 3 S matrix is given by, Scattering Matrix Calculations for 3-port JunctionA 3-port network S matrix contains 9 elements in a 3 × 3 arrangement. There are two types of 3-port junctions: E-plane tee and H-plane tee. 3.6 E plane, H-plane and E-H (Magic Tee)E-Plane TeeThere is a change of structure in the E plane (that is the side-arm port is in the E plane) so it is called an E-plane tee. It is also called as a series junction or voltage junction. In a long wave guide, a rectangular slot is cut along the broader dimension and a side arm is attached to it as shown in Figure. The coplanar arms are the two arms that are in line, while the other arm attached to it is called sidearm or E arm or series arm.
Scattering Matrix Calculations for 3-port JunctionA 3-port network S matrix contains 9 elements in a 3 × 3 arrangement. There are two types of 3-port junctions: E-plane tee and H-plane tee. 3.6 E plane, H-plane and E-H (Magic Tee)E-Plane TeeThere is a change of structure in the E plane (that is the side-arm port is in the E plane) so it is called an E-plane tee. It is also called as a series junction or voltage junction. In a long wave guide, a rectangular slot is cut along the broader dimension and a side arm is attached to it as shown in Figure. The coplanar arms are the two arms that are in line, while the other arm attached to it is called sidearm or E arm or series arm.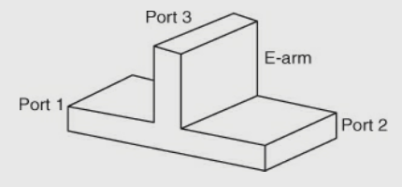 The scattering matrix can be derived as follows: Since the E-plane tee is a three-port junction, it should be a 3 × 3 square matrix as given below,
The scattering matrix can be derived as follows: Since the E-plane tee is a three-port junction, it should be a 3 × 3 square matrix as given below, (1)Due to the plane of symmetry of junction, scattering coefficient outputs at port (1) and (2) are 180° out of phase with the input at port (3),
(1)Due to the plane of symmetry of junction, scattering coefficient outputs at port (1) and (2) are 180° out of phase with the input at port (3), 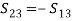 Symmetry property,
Symmetry property,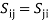
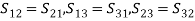 If port (3) is perfectly matched to the junction, then, S33 = 0,With the above properties, [S] can be written as,
If port (3) is perfectly matched to the junction, then, S33 = 0,With the above properties, [S] can be written as,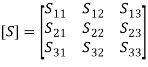 (2)That is, we have four unknown parametersFrom the unitary property, we have,
(2)That is, we have four unknown parametersFrom the unitary property, we have,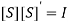
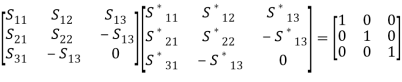
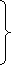 Briefly, from the unitary property, we can say that the sum of products of elements of the column of the S matrix is equal to 1.
Briefly, from the unitary property, we can say that the sum of products of elements of the column of the S matrix is equal to 1.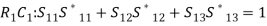
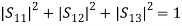 (3)
(3) 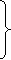

 (4)
(4)
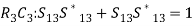
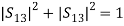 (5)
(5)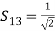 (6)Comparing equations, we get,S11 = S22
(6)Comparing equations, we get,S11 = S22 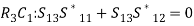
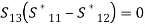
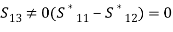 and,
and, 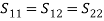 (7)By substituting Eqs. (6) and (7) in Eq. (3), we get,
(7)By substituting Eqs. (6) and (7) in Eq. (3), we get, therefore S11 =
therefore S11 =  Substituting the values of S11, S12, S13, S22 from the above equations, we get the resultant S matrix for the E-plane tee, which is,
Substituting the values of S11, S12, S13, S22 from the above equations, we get the resultant S matrix for the E-plane tee, which is,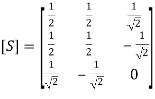 (8) H-Plane TeeSince the side-arm port is in the H plane, it is called an H-plane tee. It is also called a current junction, shunt junction, or parallel junction. A rectangular slot is cut along the width (along b) of a long wave guide, and a side arm is attached as shown in the figure. The coplanar arms are the two arms that are in line, while the other arm which is attached to side is called a side arm or H arm or shunt arm.The H-plane tee is a three-port junction. So, its S matrix should be a 3 × 3 matrix. Let it be
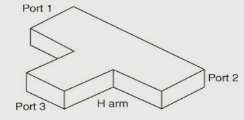
(8) H-Plane TeeSince the side-arm port is in the H plane, it is called an H-plane tee. It is also called a current junction, shunt junction, or parallel junction. A rectangular slot is cut along the width (along b) of a long wave guide, and a side arm is attached as shown in the figure. The coplanar arms are the two arms that are in line, while the other arm which is attached to side is called a side arm or H arm or shunt arm.The H-plane tee is a three-port junction. So, its S matrix should be a 3 × 3 matrix. Let it be 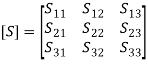 (9)
(9)  Since the plane of symmetry of junction, then, S13 = S23Symmetry property, therefore, Sij = Sjitherefore, S12 = S21, S13 = S31, S23 = S32Port (3) is perfectly matched to junction, therefore, S33 = 0,With the above properties, [S] can be written as,
Since the plane of symmetry of junction, then, S13 = S23Symmetry property, therefore, Sij = Sjitherefore, S12 = S21, S13 = S31, S23 = S32Port (3) is perfectly matched to junction, therefore, S33 = 0,With the above properties, [S] can be written as,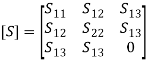 (10)That is, we have four unknown parameters as per Eq. (10). From unitary property,
(10)That is, we have four unknown parameters as per Eq. (10). From unitary property, 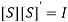
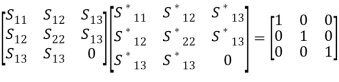
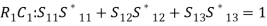
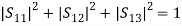 (11)
(11) 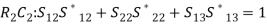
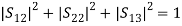 (12)
(12)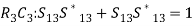 (13)
(13)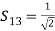 (14)Comparing Eqs. (13) and (14), we get,S11 = S22
(14)Comparing Eqs. (13) and (14), we get,S11 = S22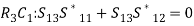 (15)
(15)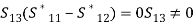
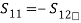
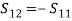 Using these in Eq. (13), we get,
Using these in Eq. (13), we get, Substituting the values of S11, S12, S13, S22 from the above equations, we get the resultant S matrix for the H-plane tee, which is given by,
Substituting the values of S11, S12, S13, S22 from the above equations, we get the resultant S matrix for the H-plane tee, which is given by,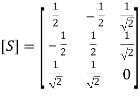 (16) SCATTERING MATRIX CALCULATIONS FOR 4-PORT JUNCTIONThe S matrix of a 4-port network consists of 16 elements in 4 × 4 square matrix. The matrix is symmetric and unitary. Compared to 3-port network, a 4-port network can be lossless, reciprocal, and matched at all ports simultaneously.Magic TeeBy connecting the sidewalls to the slots cut in the narrow wall and the broad wall of a piece of a waveguide, a magic tee is formed. As a structure, it is a combination of the E-plane tee and the H-plane tee. It is a kind of hybrid where the power is divided equally among the output ports. There can be a phase difference of 0° or a 180° in the outputs. One of the major benefits of the magic tee is that the power delivered to one port is not affected by the termination at the other output port given that the other port is match terminated.
(16) SCATTERING MATRIX CALCULATIONS FOR 4-PORT JUNCTIONThe S matrix of a 4-port network consists of 16 elements in 4 × 4 square matrix. The matrix is symmetric and unitary. Compared to 3-port network, a 4-port network can be lossless, reciprocal, and matched at all ports simultaneously.Magic TeeBy connecting the sidewalls to the slots cut in the narrow wall and the broad wall of a piece of a waveguide, a magic tee is formed. As a structure, it is a combination of the E-plane tee and the H-plane tee. It is a kind of hybrid where the power is divided equally among the output ports. There can be a phase difference of 0° or a 180° in the outputs. One of the major benefits of the magic tee is that the power delivered to one port is not affected by the termination at the other output port given that the other port is match terminated. Let there be a magic tee with port designations as shown in the diagram above. Since Magic tee is a four port junction, its s-matrix is a 4 × 4 square matrix. Let the matrix be given by,
Let there be a magic tee with port designations as shown in the diagram above. Since Magic tee is a four port junction, its s-matrix is a 4 × 4 square matrix. Let the matrix be given by,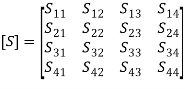 (17) All the four ports are perfectly matched to the junction, so S11 = S22 = S33 = S44 = 0. The ports (1) (2) and (3) (4) are perfectly isolated; that is, S12 = S21= S34 = S43 = 0, as the junction is ideal and it is reciprocal. So, the matrix is symmetrical; that is, Sij = Sji, for i ≠ j; that is, S23 = S32, S13 = S31, S24 = S42, S34 = S43, S41 = S14, and S12 = S21,Due to the E-plane tee junction, S23 = −S13, as scattering coefficient outputs at ports 1 and 2 are 180° out of phase with the input at port (3); the H-plane tee at port 4 is asymmetrical with ports 1 and 2, so S24 = S14Incorporating the above aspects, we have,
(17) All the four ports are perfectly matched to the junction, so S11 = S22 = S33 = S44 = 0. The ports (1) (2) and (3) (4) are perfectly isolated; that is, S12 = S21= S34 = S43 = 0, as the junction is ideal and it is reciprocal. So, the matrix is symmetrical; that is, Sij = Sji, for i ≠ j; that is, S23 = S32, S13 = S31, S24 = S42, S34 = S43, S41 = S14, and S12 = S21,Due to the E-plane tee junction, S23 = −S13, as scattering coefficient outputs at ports 1 and 2 are 180° out of phase with the input at port (3); the H-plane tee at port 4 is asymmetrical with ports 1 and 2, so S24 = S14Incorporating the above aspects, we have,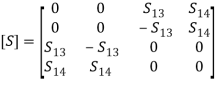 (18) Since the junction is ideal, it should be lossless and its S matrix is unitary. Therefore,
(18) Since the junction is ideal, it should be lossless and its S matrix is unitary. Therefore,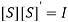
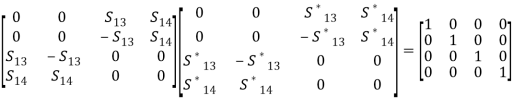 R3C3 :
R3C3 :  resulting in S13 = 1/√2 R4C4 :
resulting in S13 = 1/√2 R4C4 :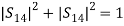 resulting in S14 =1/√2Then, the resultant S matrix for the magic tee is
resulting in S14 =1/√2Then, the resultant S matrix for the magic tee is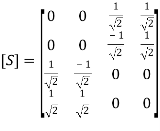 (19) 3.7 Tees, Directional Coupler, Isolator and Circulator, Related ProblemsDirectional CouplersThe directional coupler is a passive, reciprocal four-port network. In a four-port coupler, the power incident at one port (the input) is split between two other ports (the coupled and through ports), and little or no power emerges from the third port (isolated port). The schematic of the directional coupler is shown in the figure below,
(19) 3.7 Tees, Directional Coupler, Isolator and Circulator, Related ProblemsDirectional CouplersThe directional coupler is a passive, reciprocal four-port network. In a four-port coupler, the power incident at one port (the input) is split between two other ports (the coupled and through ports), and little or no power emerges from the third port (isolated port). The schematic of the directional coupler is shown in the figure below,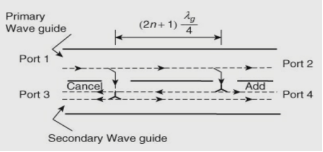 ( FIGURE A )
( FIGURE A ) 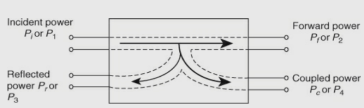 ( FIGURE B ) The power incident at port1 is divided to through the port (port 2) and coupled port (port 4) but not to the isolated port (port 3). Similarly, power incident at port (2) is divided to (1) and (3) but not to (4), power incident at port (3) is divided to (4) and (2) but not to (1), power incident at port (4) is divided to (3) and (1) but not to (2). As the directional coupler is a four port junction its S-matrix is a 4 × 4 square matrix given by,
( FIGURE B ) The power incident at port1 is divided to through the port (port 2) and coupled port (port 4) but not to the isolated port (port 3). Similarly, power incident at port (2) is divided to (1) and (3) but not to (4), power incident at port (3) is divided to (4) and (2) but not to (1), power incident at port (4) is divided to (3) and (1) but not to (2). As the directional coupler is a four port junction its S-matrix is a 4 × 4 square matrix given by,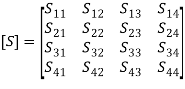 (20) All four ports are perfectly matched to the junction; that is, all diagonal elements are zero.Sii = 0From the symmetry property,Sij = Sji, that is ,
(20) All four ports are perfectly matched to the junction; that is, all diagonal elements are zero.Sii = 0From the symmetry property,Sij = Sji, that is ,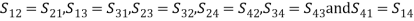 Ideally, there is no back power (Pb = 0); ports 1 and 3, ports 2 and 4 are decoupled (isolated)
Ideally, there is no back power (Pb = 0); ports 1 and 3, ports 2 and 4 are decoupled (isolated)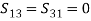
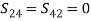
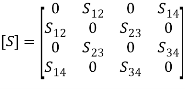 (21)
(21)
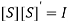

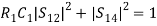 (22a)
(22a) 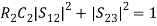 (22b)
(22b) 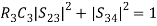 (22c)
(22c)  (22d)Comparing Eqs. (22a) and (22b), we have, S14 = S23, Comparing Eqs.( 22b) and (22c), we have, S12 = S34,Let us assume S12is real and positive = ‘p’
(22d)Comparing Eqs. (22a) and (22b), we have, S14 = S23, Comparing Eqs.( 22b) and (22c), we have, S12 = S34,Let us assume S12is real and positive = ‘p’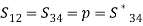 From Eqn. (22d), we have,
From Eqn. (22d), we have, 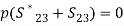 therefore, S23 should be imaginary
therefore, S23 should be imaginary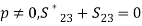 Or
Or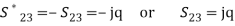 where q is real and positive.
where q is real and positive.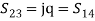
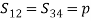 Substituting the values of unknown parameters from the above equations, we get the resultant S matrix for the directional coupler, which is,
Substituting the values of unknown parameters from the above equations, we get the resultant S matrix for the directional coupler, which is, (23) Circulators A microwave circulator has three or more ports and it is a non-reciprocal ferrite device. The input given at port n will come out at port n +1 but cannot come at any other port. A Y-junction circulator is the widely used device which is a three-port ferrite junction circulator. It is a passive device. However it shows some characteristics that make it behave almost like a active device. A 3-port clockwise circulator is shown in the figure below,
(23) Circulators A microwave circulator has three or more ports and it is a non-reciprocal ferrite device. The input given at port n will come out at port n +1 but cannot come at any other port. A Y-junction circulator is the widely used device which is a three-port ferrite junction circulator. It is a passive device. However it shows some characteristics that make it behave almost like a active device. A 3-port clockwise circulator is shown in the figure below,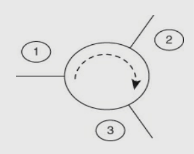 For a 3-port circulator, the S matrix is a 3 × 3 matrix.
For a 3-port circulator, the S matrix is a 3 × 3 matrix.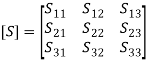 (24)All the three ports are perfectly matched to the junction.
(24)All the three ports are perfectly matched to the junction.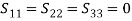 A circulator obeys the non-reciprocity and lossless condition, since it has ferrite material at the junction. From the unitary property,
A circulator obeys the non-reciprocity and lossless condition, since it has ferrite material at the junction. From the unitary property,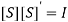
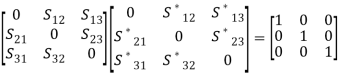
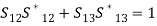
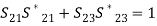
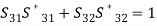
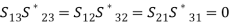 (25)Let us consider S21 ≠ 0; from the above Eq. (25), we get,S13 = S21 = S32 = 1,S31 = S12 = S23 = 0 Substituting the values of unknown parameters from the above equations, we get the resultant S matrix for the circulator, which is given by,
(25)Let us consider S21 ≠ 0; from the above Eq. (25), we get,S13 = S21 = S32 = 1,S31 = S12 = S23 = 0 Substituting the values of unknown parameters from the above equations, we get the resultant S matrix for the circulator, which is given by,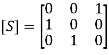 (26) Anti-clockwise circulator A 3-port anti-clockwise circulator is shown in the figure below,
(26) Anti-clockwise circulator A 3-port anti-clockwise circulator is shown in the figure below,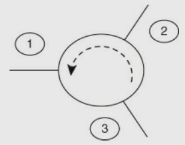 For an anti-clockwise circulator from non-reciprocal S13 = S21 = S32 = 0, S31 = S12 = S23 = 1 We get the resultant S matrix for the anti-clockwise circulator, which is given by,
For an anti-clockwise circulator from non-reciprocal S13 = S21 = S32 = 0, S31 = S12 = S23 = 1 We get the resultant S matrix for the anti-clockwise circulator, which is given by,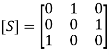 (27) IsolatorsAn isolator is a two-port device with input and output ports. It is nothing but a circulator with third port being terminated. An isolator is shown in the figure below,
(27) IsolatorsAn isolator is a two-port device with input and output ports. It is nothing but a circulator with third port being terminated. An isolator is shown in the figure below,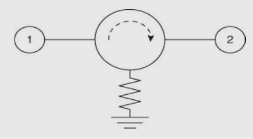 Since an isolator is a two-port component, the S matrix should be a 2 × 2 matrix given by,
Since an isolator is a two-port component, the S matrix should be a 2 × 2 matrix given by,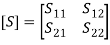 Two ports are perfectly matched to the junction; that is, the diagonal elements are zero.therefore, Sii = 0, i.e., S11 = S22 = 0, Isolators usually have ferrite material at the junction to cause the non-reciprocity condition. When the S matrix is non reciprocal (Sij ≠ Sji), the conditions of port match and losslessness apply. In microwave applications, an isolator is used between a high power source and a load which prevents possible reflections that may damage the source. Isolators always follow the source. If the source is at port 1, its purpose is to prevent the reflected wave from port 2; that is, S12 = 0. The S matrix for an ideal isolator is given by,
Two ports are perfectly matched to the junction; that is, the diagonal elements are zero.therefore, Sii = 0, i.e., S11 = S22 = 0, Isolators usually have ferrite material at the junction to cause the non-reciprocity condition. When the S matrix is non reciprocal (Sij ≠ Sji), the conditions of port match and losslessness apply. In microwave applications, an isolator is used between a high power source and a load which prevents possible reflections that may damage the source. Isolators always follow the source. If the source is at port 1, its purpose is to prevent the reflected wave from port 2; that is, S12 = 0. The S matrix for an ideal isolator is given by,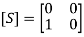 If the source is at port 2, its purpose is to prevent the reflected wave from port 1; that is, S21 = 0,The S matrix for an ideal isolator is given by,
If the source is at port 2, its purpose is to prevent the reflected wave from port 1; that is, S21 = 0,The S matrix for an ideal isolator is given by,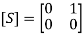 Reference Books1. M. Kulkarni, “Microwave and Radar engineering”, 3rd edition, Umesh Publications.2. ML Sisodia& GS Raghuvamshi, “Microwave Circuits and Passive Devices”Wiley, 1987.3. M L Sisodia& G S Raghuvanshi, “Basic Microwave Techniques and Laboratory Manual”, New Age International (P) Limited, Publishers.
Reference Books1. M. Kulkarni, “Microwave and Radar engineering”, 3rd edition, Umesh Publications.2. ML Sisodia& GS Raghuvamshi, “Microwave Circuits and Passive Devices”Wiley, 1987.3. M L Sisodia& G S Raghuvanshi, “Basic Microwave Techniques and Laboratory Manual”, New Age International (P) Limited, Publishers.
 Transfer Matrix or the Transmission Matrix (ABCD)The transfer matrix also known as ABCD matrix relates the voltage and current at port 1 to those at port 2. In equation form; V1 = AV2 + BI2 and
Transfer Matrix or the Transmission Matrix (ABCD)The transfer matrix also known as ABCD matrix relates the voltage and current at port 1 to those at port 2. In equation form; V1 = AV2 + BI2 and  Vi+, Ii+, Vi-, and Ii- are the complex amplitudes of sinusoidal excitations. The power of the entering or leaving wave is given by the product of the voltage and current. The characteristic impedance (Z0) of the port is given by the ratio of the voltage and current. The total voltage and the total current at port i are as follows:
Vi+, Ii+, Vi-, and Ii- are the complex amplitudes of sinusoidal excitations. The power of the entering or leaving wave is given by the product of the voltage and current. The characteristic impedance (Z0) of the port is given by the ratio of the voltage and current. The total voltage and the total current at port i are as follows: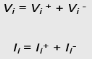 When a voltage wave (Vi+) is incident at one port, some fraction of the signal bounces back out of that port, some of it scatters and exits from other ports, and some of it disappears as heat or electromagnetic radiation. Usually, all the microwave network ports have similar connectors (coaxial connectors or waveguide flanges) with an impedance of 50 Ω, and the characteristic impedances (Z0) of the ports have a similar value. However, in a general case, the characteristic impedances (Z0) may have different values. For example, the ports of a coaxial-to-waveguide adapter have different characteristic impedances. Then, the voltage waves should be normalized. S-PARAMETER REPRESENTATION OF A 2 - PORT NETWORKThe behaviour of the network in terms of the injected and reflected power waves can be described by a set of linear equations. For the 2-port case, the outputs can be related to the inputs by,b1 = S11a1 + S12a2b2 = S21a1 + S22a2where b1 is the wave travelling away from port 1 (i.e. toward source) = wave incident on port 1 times the reflection coefficient (S11a1) + wave incident on port 2 times transmission coefficient from port 2 to port 1 (S12a2). Similarly, b2 is the wave traveling away from port 2 = S21a1 + S22a2. From the above equations, we can say that each signal coming out of a two-port network (i.e. b1 or b2) will have two components: some signal reflected from the same port and some signal transferred from the other port. We can interpret Sij as the power measured at port i due to the incident power at port j. The term Sij can be computed directly by the following formula:
When a voltage wave (Vi+) is incident at one port, some fraction of the signal bounces back out of that port, some of it scatters and exits from other ports, and some of it disappears as heat or electromagnetic radiation. Usually, all the microwave network ports have similar connectors (coaxial connectors or waveguide flanges) with an impedance of 50 Ω, and the characteristic impedances (Z0) of the ports have a similar value. However, in a general case, the characteristic impedances (Z0) may have different values. For example, the ports of a coaxial-to-waveguide adapter have different characteristic impedances. Then, the voltage waves should be normalized. S-PARAMETER REPRESENTATION OF A 2 - PORT NETWORKThe behaviour of the network in terms of the injected and reflected power waves can be described by a set of linear equations. For the 2-port case, the outputs can be related to the inputs by,b1 = S11a1 + S12a2b2 = S21a1 + S22a2where b1 is the wave travelling away from port 1 (i.e. toward source) = wave incident on port 1 times the reflection coefficient (S11a1) + wave incident on port 2 times transmission coefficient from port 2 to port 1 (S12a2). Similarly, b2 is the wave traveling away from port 2 = S21a1 + S22a2. From the above equations, we can say that each signal coming out of a two-port network (i.e. b1 or b2) will have two components: some signal reflected from the same port and some signal transferred from the other port. We can interpret Sij as the power measured at port i due to the incident power at port j. The term Sij can be computed directly by the following formula:
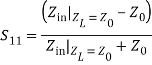 From the above equation, we can say that the reflection coefficient (S11) is the method of specifying the input impedance Zin.S11 = b1/a1 that is, the input reflection coefficient (when a2 = 0) S21 = b2/a1 that is, the forward transmission gain/loss (when a2 = 0) Determination of S22, S12 parameters: S22, S12 parameters can be computed, if port 1 is terminated with a matched load (Z0). Then, the incident wave at port 1 (i.e. a1) becomes zero (a1 = 0), and the wave leaving port 1 (i.e. b1) is presented (see figure). The b1 is the wave travelling away from port 1 and is due to the wave incident at port 2 (i.e. a2) times the transmission factor (S12) from port 2 to port 1. Similarly, b2 is the wave travelling away from port 2 toward the source and is due to the wave incident at port 2 (i.e. a2) times the reflection coefficient (S22).
From the above equation, we can say that the reflection coefficient (S11) is the method of specifying the input impedance Zin.S11 = b1/a1 that is, the input reflection coefficient (when a2 = 0) S21 = b2/a1 that is, the forward transmission gain/loss (when a2 = 0) Determination of S22, S12 parameters: S22, S12 parameters can be computed, if port 1 is terminated with a matched load (Z0). Then, the incident wave at port 1 (i.e. a1) becomes zero (a1 = 0), and the wave leaving port 1 (i.e. b1) is presented (see figure). The b1 is the wave travelling away from port 1 and is due to the wave incident at port 2 (i.e. a2) times the transmission factor (S12) from port 2 to port 1. Similarly, b2 is the wave travelling away from port 2 toward the source and is due to the wave incident at port 2 (i.e. a2) times the reflection coefficient (S22). Mathematically, the above statements can be written, as the same analysis and comments clearly apply to S22.By symmetry,
Mathematically, the above statements can be written, as the same analysis and comments clearly apply to S22.By symmetry,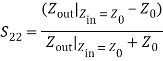 From the above equation, we can say that the reflection coefficient (S22) is the method of specifying the output impedance Z0:S22 = b2/a2; that is, the output reflection coefficient (when a1 = 0) S12 = b1/a2; that is, the reverse transmission gain/loss (when a1 = 0)a1 and b1 are rms voltages normalized by √Z0 and S22 are the reflection coefficients with the opposite port terminated at Z0. S21 and S12are the forward and reverse transducer gains, respectively. S Parameters for 3 PortsA 3-port network is shown in the figure. The matrix equations for a 3-port network are as follows: b1 = S11a1 + S12a2 + S13a3b2 = S21a1 + S22a2 + S23a3b3 = S31a1 + S32a2 + S33a3 In matrix form,
From the above equation, we can say that the reflection coefficient (S22) is the method of specifying the output impedance Z0:S22 = b2/a2; that is, the output reflection coefficient (when a1 = 0) S12 = b1/a2; that is, the reverse transmission gain/loss (when a1 = 0)a1 and b1 are rms voltages normalized by √Z0 and S22 are the reflection coefficients with the opposite port terminated at Z0. S21 and S12are the forward and reverse transducer gains, respectively. S Parameters for 3 PortsA 3-port network is shown in the figure. The matrix equations for a 3-port network are as follows: b1 = S11a1 + S12a2 + S13a3b2 = S21a1 + S22a2 + S23a3b3 = S31a1 + S32a2 + S33a3 In matrix form,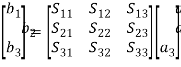

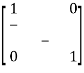 Examples of S Matrices1-port S matrixConsider 1-Port as simple lumped elements and cavities with one test port, long transmission lines or antennas. 1-port S-matrix is a matrix consisting of a single element, and the single element is the scattering parameter or reflection coefficient. It can be a 1×1 matrix; one row and one column.1-port is characterized by their reflection coefficient (Γ), or in terms of S parameters, S11.Ideal short for 1-port is given by S11 = −1 Ideal termination is given by S11 = 0 Active termination or reflection amplifier is given by |S11| > 1 2-port S MatrixAn isolator is a 2-port device. Both the ports are perfectly matched to the junction, that is, the diagonal elements are zero. Sii = 0, that is, S11 = S22 = 0, and the junction is non reciprocal (Sij ≠ Sji). Hence, if the source is at port (1), its purpose is to prevent the reflected wave from port (2), that is, S12 = 0The S matrix for an ideal isolator is,
Examples of S Matrices1-port S matrixConsider 1-Port as simple lumped elements and cavities with one test port, long transmission lines or antennas. 1-port S-matrix is a matrix consisting of a single element, and the single element is the scattering parameter or reflection coefficient. It can be a 1×1 matrix; one row and one column.1-port is characterized by their reflection coefficient (Γ), or in terms of S parameters, S11.Ideal short for 1-port is given by S11 = −1 Ideal termination is given by S11 = 0 Active termination or reflection amplifier is given by |S11| > 1 2-port S MatrixAn isolator is a 2-port device. Both the ports are perfectly matched to the junction, that is, the diagonal elements are zero. Sii = 0, that is, S11 = S22 = 0, and the junction is non reciprocal (Sij ≠ Sji). Hence, if the source is at port (1), its purpose is to prevent the reflected wave from port (2), that is, S12 = 0The S matrix for an ideal isolator is, Scattering Matrix Calculations for 3-port JunctionA 3-port network S matrix contains 9 elements in a 3 × 3 arrangement. There are two types of 3-port junctions: E-plane tee and H-plane tee. 3.6 E plane, H-plane and E-H (Magic Tee)E-Plane TeeThere is a change of structure in the E plane (that is the side-arm port is in the E plane) so it is called an E-plane tee. It is also called as a series junction or voltage junction. In a long wave guide, a rectangular slot is cut along the broader dimension and a side arm is attached to it as shown in Figure. The coplanar arms are the two arms that are in line, while the other arm attached to it is called sidearm or E arm or series arm.
Scattering Matrix Calculations for 3-port JunctionA 3-port network S matrix contains 9 elements in a 3 × 3 arrangement. There are two types of 3-port junctions: E-plane tee and H-plane tee. 3.6 E plane, H-plane and E-H (Magic Tee)E-Plane TeeThere is a change of structure in the E plane (that is the side-arm port is in the E plane) so it is called an E-plane tee. It is also called as a series junction or voltage junction. In a long wave guide, a rectangular slot is cut along the broader dimension and a side arm is attached to it as shown in Figure. The coplanar arms are the two arms that are in line, while the other arm attached to it is called sidearm or E arm or series arm. The scattering matrix can be derived as follows: Since the E-plane tee is a three-port junction, it should be a 3 × 3 square matrix as given below,
The scattering matrix can be derived as follows: Since the E-plane tee is a three-port junction, it should be a 3 × 3 square matrix as given below, (1)Due to the plane of symmetry of junction, scattering coefficient outputs at port (1) and (2) are 180° out of phase with the input at port (3),
(1)Due to the plane of symmetry of junction, scattering coefficient outputs at port (1) and (2) are 180° out of phase with the input at port (3), 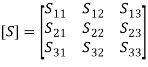 (2)That is, we have four unknown parametersFrom the unitary property, we have,
(2)That is, we have four unknown parametersFrom the unitary property, we have,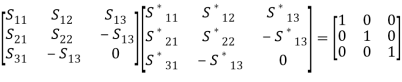
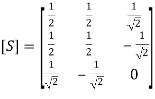 (8) H-Plane TeeSince the side-arm port is in the H plane, it is called an H-plane tee. It is also called a current junction, shunt junction, or parallel junction. A rectangular slot is cut along the width (along b) of a long wave guide, and a side arm is attached as shown in the figure. The coplanar arms are the two arms that are in line, while the other arm which is attached to side is called a side arm or H arm or shunt arm.The H-plane tee is a three-port junction. So, its S matrix should be a 3 × 3 matrix. Let it be
(8) H-Plane TeeSince the side-arm port is in the H plane, it is called an H-plane tee. It is also called a current junction, shunt junction, or parallel junction. A rectangular slot is cut along the width (along b) of a long wave guide, and a side arm is attached as shown in the figure. The coplanar arms are the two arms that are in line, while the other arm which is attached to side is called a side arm or H arm or shunt arm.The H-plane tee is a three-port junction. So, its S matrix should be a 3 × 3 matrix. Let it be 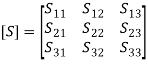 (9)
(9)  Since the plane of symmetry of junction, then, S13 = S23Symmetry property, therefore, Sij = Sjitherefore, S12 = S21, S13 = S31, S23 = S32Port (3) is perfectly matched to junction, therefore, S33 = 0,With the above properties, [S] can be written as,
Since the plane of symmetry of junction, then, S13 = S23Symmetry property, therefore, Sij = Sjitherefore, S12 = S21, S13 = S31, S23 = S32Port (3) is perfectly matched to junction, therefore, S33 = 0,With the above properties, [S] can be written as,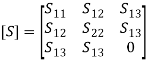 (10)That is, we have four unknown parameters as per Eq. (10). From unitary property,
(10)That is, we have four unknown parameters as per Eq. (10). From unitary property, 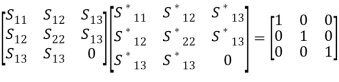
 (16) SCATTERING MATRIX CALCULATIONS FOR 4-PORT JUNCTIONThe S matrix of a 4-port network consists of 16 elements in 4 × 4 square matrix. The matrix is symmetric and unitary. Compared to 3-port network, a 4-port network can be lossless, reciprocal, and matched at all ports simultaneously.Magic TeeBy connecting the sidewalls to the slots cut in the narrow wall and the broad wall of a piece of a waveguide, a magic tee is formed. As a structure, it is a combination of the E-plane tee and the H-plane tee. It is a kind of hybrid where the power is divided equally among the output ports. There can be a phase difference of 0° or a 180° in the outputs. One of the major benefits of the magic tee is that the power delivered to one port is not affected by the termination at the other output port given that the other port is match terminated.
(16) SCATTERING MATRIX CALCULATIONS FOR 4-PORT JUNCTIONThe S matrix of a 4-port network consists of 16 elements in 4 × 4 square matrix. The matrix is symmetric and unitary. Compared to 3-port network, a 4-port network can be lossless, reciprocal, and matched at all ports simultaneously.Magic TeeBy connecting the sidewalls to the slots cut in the narrow wall and the broad wall of a piece of a waveguide, a magic tee is formed. As a structure, it is a combination of the E-plane tee and the H-plane tee. It is a kind of hybrid where the power is divided equally among the output ports. There can be a phase difference of 0° or a 180° in the outputs. One of the major benefits of the magic tee is that the power delivered to one port is not affected by the termination at the other output port given that the other port is match terminated. Let there be a magic tee with port designations as shown in the diagram above. Since Magic tee is a four port junction, its s-matrix is a 4 × 4 square matrix. Let the matrix be given by,
Let there be a magic tee with port designations as shown in the diagram above. Since Magic tee is a four port junction, its s-matrix is a 4 × 4 square matrix. Let the matrix be given by,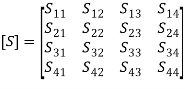 (17) All the four ports are perfectly matched to the junction, so S11 = S22 = S33 = S44 = 0. The ports (1) (2) and (3) (4) are perfectly isolated; that is, S12 = S21= S34 = S43 = 0, as the junction is ideal and it is reciprocal. So, the matrix is symmetrical; that is, Sij = Sji, for i ≠ j; that is, S23 = S32, S13 = S31, S24 = S42, S34 = S43, S41 = S14, and S12 = S21,Due to the E-plane tee junction, S23 = −S13, as scattering coefficient outputs at ports 1 and 2 are 180° out of phase with the input at port (3); the H-plane tee at port 4 is asymmetrical with ports 1 and 2, so S24 = S14Incorporating the above aspects, we have,
(17) All the four ports are perfectly matched to the junction, so S11 = S22 = S33 = S44 = 0. The ports (1) (2) and (3) (4) are perfectly isolated; that is, S12 = S21= S34 = S43 = 0, as the junction is ideal and it is reciprocal. So, the matrix is symmetrical; that is, Sij = Sji, for i ≠ j; that is, S23 = S32, S13 = S31, S24 = S42, S34 = S43, S41 = S14, and S12 = S21,Due to the E-plane tee junction, S23 = −S13, as scattering coefficient outputs at ports 1 and 2 are 180° out of phase with the input at port (3); the H-plane tee at port 4 is asymmetrical with ports 1 and 2, so S24 = S14Incorporating the above aspects, we have,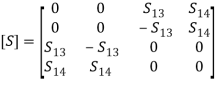 (18) Since the junction is ideal, it should be lossless and its S matrix is unitary. Therefore,
(18) Since the junction is ideal, it should be lossless and its S matrix is unitary. Therefore,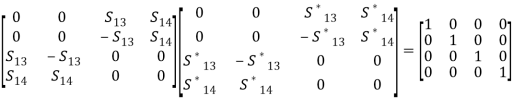 R3C3 :
R3C3 : 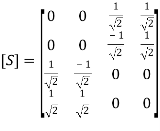 (19) 3.7 Tees, Directional Coupler, Isolator and Circulator, Related ProblemsDirectional CouplersThe directional coupler is a passive, reciprocal four-port network. In a four-port coupler, the power incident at one port (the input) is split between two other ports (the coupled and through ports), and little or no power emerges from the third port (isolated port). The schematic of the directional coupler is shown in the figure below,
(19) 3.7 Tees, Directional Coupler, Isolator and Circulator, Related ProblemsDirectional CouplersThe directional coupler is a passive, reciprocal four-port network. In a four-port coupler, the power incident at one port (the input) is split between two other ports (the coupled and through ports), and little or no power emerges from the third port (isolated port). The schematic of the directional coupler is shown in the figure below, ( FIGURE A )
( FIGURE A )  ( FIGURE B ) The power incident at port1 is divided to through the port (port 2) and coupled port (port 4) but not to the isolated port (port 3). Similarly, power incident at port (2) is divided to (1) and (3) but not to (4), power incident at port (3) is divided to (4) and (2) but not to (1), power incident at port (4) is divided to (3) and (1) but not to (2). As the directional coupler is a four port junction its S-matrix is a 4 × 4 square matrix given by,
( FIGURE B ) The power incident at port1 is divided to through the port (port 2) and coupled port (port 4) but not to the isolated port (port 3). Similarly, power incident at port (2) is divided to (1) and (3) but not to (4), power incident at port (3) is divided to (4) and (2) but not to (1), power incident at port (4) is divided to (3) and (1) but not to (2). As the directional coupler is a four port junction its S-matrix is a 4 × 4 square matrix given by,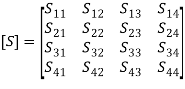 (20) All four ports are perfectly matched to the junction; that is, all diagonal elements are zero.Sii = 0From the symmetry property,Sij = Sji, that is ,
(20) All four ports are perfectly matched to the junction; that is, all diagonal elements are zero.Sii = 0From the symmetry property,Sij = Sji, that is ,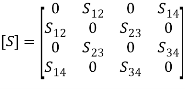 (21)
(21)
 (23) Circulators A microwave circulator has three or more ports and it is a non-reciprocal ferrite device. The input given at port n will come out at port n +1 but cannot come at any other port. A Y-junction circulator is the widely used device which is a three-port ferrite junction circulator. It is a passive device. However it shows some characteristics that make it behave almost like a active device. A 3-port clockwise circulator is shown in the figure below,
(23) Circulators A microwave circulator has three or more ports and it is a non-reciprocal ferrite device. The input given at port n will come out at port n +1 but cannot come at any other port. A Y-junction circulator is the widely used device which is a three-port ferrite junction circulator. It is a passive device. However it shows some characteristics that make it behave almost like a active device. A 3-port clockwise circulator is shown in the figure below, For a 3-port circulator, the S matrix is a 3 × 3 matrix.
For a 3-port circulator, the S matrix is a 3 × 3 matrix.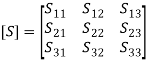 (24)All the three ports are perfectly matched to the junction.
(24)All the three ports are perfectly matched to the junction.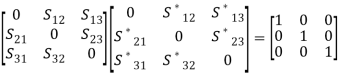
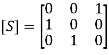 (26) Anti-clockwise circulator A 3-port anti-clockwise circulator is shown in the figure below,
(26) Anti-clockwise circulator A 3-port anti-clockwise circulator is shown in the figure below, For an anti-clockwise circulator from non-reciprocal S13 = S21 = S32 = 0, S31 = S12 = S23 = 1 We get the resultant S matrix for the anti-clockwise circulator, which is given by,
For an anti-clockwise circulator from non-reciprocal S13 = S21 = S32 = 0, S31 = S12 = S23 = 1 We get the resultant S matrix for the anti-clockwise circulator, which is given by,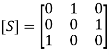 (27) IsolatorsAn isolator is a two-port device with input and output ports. It is nothing but a circulator with third port being terminated. An isolator is shown in the figure below,
(27) IsolatorsAn isolator is a two-port device with input and output ports. It is nothing but a circulator with third port being terminated. An isolator is shown in the figure below, Since an isolator is a two-port component, the S matrix should be a 2 × 2 matrix given by,
Since an isolator is a two-port component, the S matrix should be a 2 × 2 matrix given by,0 matching results found
Browse by Topics