UNIT IV
Orbital Mechanics and Lauchers
Telstar1, was launched which was the world’s first active communications satellite in 1962.
Telesat’s predecessors at AT&T and Bell Laboratories built this satellite. During the seven months of operation, Telstar1 dazzled the world with live images of sports, entertainment and news.
It was a simple single-transponder low-earth-orbit (LEO) satellite, but its technology of receiving radio signals from the ground, and then amplifying and retransmitting them over a large portion of the earth's surface, set the standard for all communications satellites that followed.
During the 1960s and 1970s, advances in satellite performance came quickly and a global industry began to develop. Satellites were mainly used at first for international and long-haul telephone traffic and distribution of select television programming, both internationally and domestically.
In 1973, the Canadian Broadcasting Corporation began distributing its video programming to Canadian customers using Telesat’s Anik A satellite. Then in 1975 HBO began distributing its video programming to US customers by satellite.
The commercial and technical success of these ventures led to greater use and acceptance of satellite broadcasting. Later ,by 1990s, satellite communications would be the primary means of distributing TV programs around the world.
The path of satellite revolving around the earth is known as orbit. This path is represented with mathematical notations. Orbital mechanics is the study of the motion of the satellites present in orbits.
Orbital Elements
Orbital elements are the parameters, which are helpful for describing the orbital motion of satellites. Following are the orbital elements.
- Semi major axis
- Eccentricity
- Mean anomaly
- Argument of perigee
- Inclination
- Right ascension of ascending node
The above six orbital elements define the orbit of earth satellites. Therefore, it is easy to discriminate one satellite from other satellites based on the values of orbital elements.
Semi major axis
The length of semi-major axis (a) defines the size of satellite’s orbit. It is half of the major axis. This runs from the center through a focus to the edge of the ellipse. So, it is the radius of an orbit at the orbit's two most distant points.
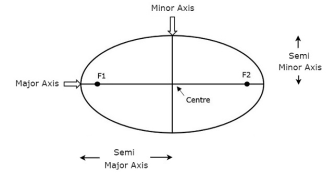
Both semi major axis and semi-minor axis are represented in above figure. Length of semi major axis (a) not only determines the size of satellite’s orbit, but also time period of revolution.
If circular orbit is taken as special case, then the length of semi-major axis will be equal to radius of that circular orbit.
Eccentricity
The value of Eccentricity (e) fixes the shape of satellite’s orbit. This parameter indicates the deviation of the orbit’s shape from a perfect circle.
If the lengths of semi major axis and semi minor axis of an elliptical orbit are a & b, then the mathematical expression for eccentricity (e) will be
e= √a2−b2/a --------------------(1)
The value of eccentricity of a circular orbit is zero, since both a & b are equal. Whereas, the value of eccentricity of an elliptical orbit lies between zero and one.
The following figure shows the various satellite orbits for different eccentricity (e) values
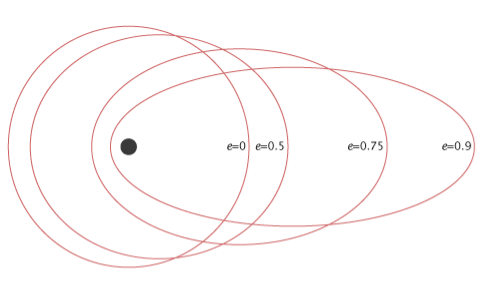
In above figure, the satellite orbit corresponding to eccentricity (e) value of zero is a circular orbit. And, the remaining three satellite orbits are of elliptical corresponding to the eccentricity (e) values 0.5, 0.75 and 0.9.
Mean Anomaly
For a satellite, the point which is closest from the Earth is known as Perigee. Mean anomaly (M) gives the average value of the angular position of the satellite with reference to perigee.
If the orbit is circular, then Mean anomaly gives the angular position of the satellite in the orbit. But, if the orbit is elliptical, then calculation of exact position is very difficult. At that time, Mean anomaly is used as an intermediate step.
Argument of Perigee
Satellite orbit cuts the equatorial plane at two points. First point is called as descending node, where the satellite passes from the northern hemisphere to the southern hemisphere. Second point is called as ascending node, where the satellite passes from the southern hemisphere to the northern hemisphere.
Argument of perigee (ω) is the angle between ascending node and perigee. If both perigee and ascending node are existing at same point, then the argument of perigee will be zero degrees.
Argument of perigee is measured in the orbital plane at earth’s center in the direction of satellite motion.
Inclination
The angle between orbital plane and earth’s equatorial plane is known as inclination (i). It is measured at the ascending node with direction being east to north. So, inclination defines the orientation of the orbit by considering the equator of earth as reference.
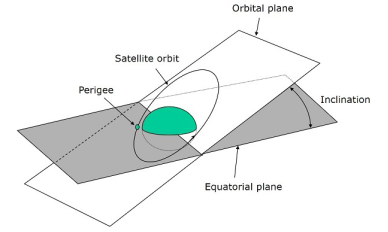
There are four types of orbits based on the angle of inclination.
- Equatorial orbit − Angle of inclination is either zero degrees or 180 degrees.
- Polar orbit − Angle of inclination is 90 degrees.
- Prograde orbit − Angle of inclination lies between zero and 90 degrees.
- Retrograde orbit − Angle of inclination lies between 90 and 180 degrees.
Right Ascension of Ascending node
We know that ascending node is the point, where the satellite crosses the equatorial plane while going from the southern hemisphere to the northern hemisphere.
Right Ascension of ascending node (Ω) is the angle between line of Aries and ascending node towards east direction in equatorial plane. Aries is also called as vernal and equinox.
Satellite’s ground track is the path on the surface of the Earth, which lies exactly below its orbit. The ground track of a satellite can take a number of different forms depending on the values of the orbital elements.
Orbital Equations
In this section, let us discuss about the equations which are related to orbital motion.
Forces acting on Satellite
A satellite, when it revolves around the earth, it undergoes a pulling force from the earth due to earth’s gravitational force. This force is known as Centripetal force (F1) because this force tends the satellite towards it.
Mathematically, the Centripetal force (F1) acting on satellite due to earth can be written as
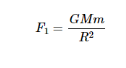
Where,
- G is universal gravitational constant and it is equal to 6.673 x 10-11 N∙m2/kg2.
- M is mass of the earth and it is equal to 5.98 x 1024 Kg.
- m is mass of the satellite.
- R is the distance from satellite to center of the Earth.
A satellite, when it revolves around the earth, it undergoes a pulling force from the sun and the moon due to their gravitational forces. This force is known as Centrifugal force (F2) because this force tends the satellite away from earth.
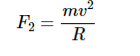
Where, v is the orbital velocity of satellite.
Orbital Velocity
Orbital velocity of satellite is the velocity at which, the satellite revolves around earth. Satellite doesn’t deviate from its orbit and moves with certain velocity in that orbit, when both Centripetal and Centrifugal forces are balance each other.
So, equate Centripetal force (F1) and Centrifugal force (F2).
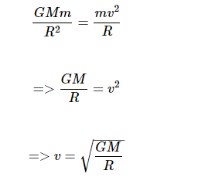
Where,
- G is gravitational constant and it is equal to 6.673 x 10-11 N∙m2/kg2.
- M is mass of the earth and it is equal to 5.98 x 1024 Kg.
- R is the distance from satellite to center of the Earth.
So, the orbital velocity mainly depends on the distance from satellite to center of the Earth (R), since G & M are constants.
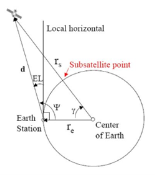
The coordinates to which an ES must point to communicate with a satellite . These are azimuth (AZ) and elevation angle(EL) is called the look angle.
- AZ : The angle measured from N to E to projection of satellite path onto horizontal plane.
- EL : The angle measured from the horizontal plane to the orbit plane.
The sub satellite point: The point on the earth’s surface of intersection between a line from the earth’s center to the satellite.
For calculating look angle:
- We require six orbital elements
- Calculate the orbit from these orbital elements
- Define the orbital plane
- Locate satellite at time t with respect to the First Point of Aries
- Find location of the Greenwich Meridian relative to the first point of Aries
- Use Spherical Trigonometry to find position of the satellite relative to a point on the earth’s surface.
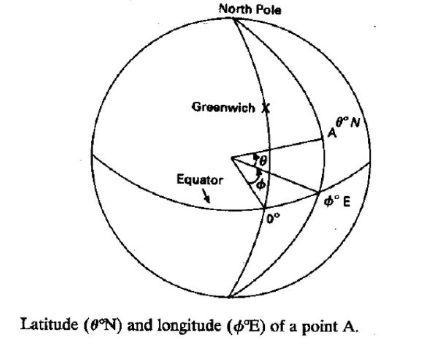
- Coordinate System
Latitude : Angular distance measured in degrees , north or south of the equator. L from -90 to + 90 (or from 90S to 90N)
Longitude : Angular distance measured in degrees from a given reference longitudinal line. (Greenwich, London) l from 0 to 360E(or 180W to 180E)
Geometry of elevation angle:
The plane in the picture includes the center of the earth ,Earth Station and satellite. Sub-
Satellite point will also be on the same plane.
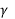is defined so that it is non-negative then
Cos (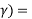
cos (Le) cos(Ls ) cos(ls – le) + sin(Le) sin(Ls)
The magnitude of the vectors joining the center of the earth, the satellite and the earth station are related by the law of cosine:
d = rs [ 1 + ( re/rs) 2 -2 (re/rs) cos(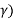
] ½
Elevation angle calculation:
By sine law
Rs / sin ( Ψ ) = d/ sin(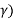
Which yields
Cos(El) = sin (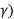
/ [ 1 + (re/rs) 2 – 2 (re/rs) cos (
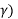] ½
Problem :
Using rs = 42,164 km and re = 678.14km gives d = 42,164[1.0228826 – 0.3025396 cos(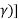
½ km which finally gives the elevation angle as
Cos(El) = sin(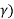
/ [ 1 + (re/rs) 2 – 2 (re/rs) cos (
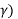] ½
Azimuth angle calculation:
More complex approach for non-geo satellites
Different formulas and correction apply depending on the combination of positions of the earth station and sub satellite point with relation to each of the four quadrants (NW,NE,SW,SE)
Its calculation is simple for geo satellites.
Find the elevation and azimuth calculation for geo satellite:
Earth Station latitude 52 0 N
Earth Station Longitude 00
Satellite Lattitude 0o
Satellite Longitude 66 0 E
Find the central angle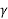 
Cos(
= cos (Le) cos(ls-le)
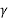= 75.4981 o
= cos(52) cos(66)
= 0.2504
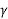= 75.4981 o
El = 5.85 0
For intermediate angle α
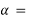tan -1 [ tan | ls – le) | / sin (Le)
= tan -1 [ tan(66-0))/ sin(52)]
= 70.6668
The earth station is in the Northern hemisphere and the satellite is to the South East of the earth station. This gives
Az = 180 -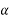 
= 180 – 70.6668 = 109.333 0 (clockwise from true North)
The look-angle to the satellite are :
Elevation angle = 5.85 0
Azimuth angle = 109.33 0
An orbit described by Kepler is ideal as Earth is considered to be a perfect sphere and the force acting around the Earth is the centrifugal force. This force is supposed to balance the gravitational pull of the earth.
In reality, other forces also play an important role and affect the motion of the satellite. These forces are the gravitational forces of Sun and Moon along with the atmospheric drag.
There are two types of Orbital Perturbations:
- The gravitational when considering the third body interaction and the non-spherical shape of the earth.
- Non-gravitational like atmospheric drag , solar radiation and pressure and tidal friction.
These can be classified as conservative or non-conservative disturbance of forces. While conservative depends only on position, non-conservative depends on both position and velocity.
Following are the orbital perturbations due to gravitational and non-gravitational forces or parameters.
- Irregular gravitational force around the Earth due to non-uniform mass distribution. Earth’s magnetic field too causes orbital perturbations.
- Main external perturbations come from Sun and Moon. When a satellite is near to these external bodies, it receives a stronger gravitational pull.
- Low-orbit satellites get affected due to friction caused by collision with atoms and ions.
- Solar radiation pressure affects large GEO satellites, which use large solar arrays.
- Self-generated torques and pressures caused by RF radiation from the antenna.
Most satellites use propulsion subsystem in order to maintain a proper spin axis direction and control the altitude of the satellite against perturbation forces.
- There are three basic strategies that are used to determine the LEO orbits with GPS. They are dynamic, kinematic or non-dynamic and hybrid or reduced dynamic strategies.
- The dynamic orbit determination approach requires precise models of the forces acting on user object. This technique was applied to many successful space vehicle missions and has become the mainstream of precision OD (POD) approach.
- Dynamic model errors are the limiting factor for this technique, such as the geopotential model errors and atmospheric drag model errors, depending on the dynamic environment of the user space vehicle.
- With the continuous, global, and high precision GPS tracking data, dynamic model parameters, such as geo potential parameters, can be used to tune effectively and reduce the effects of dynamic model error in the context of dynamic approach.
- The dense tracking data also allows frequent estimation of empirical parameters to absorb the effects of unmodeled or mis-modeled dynamic errors.
- The kinematic or geometric approach does not require the description of the dynamics except for possible interpolation between solution points for the user object, and the orbit solution is referenced to the phase center of the on-board GPS antenna instead of the space vehicle's center of mass.
- A hybrid dynamic and kinematic OD strategy would down weight the errors caused by each strategy but still utilize the strengths of each. One such strategy devised and is referred to as reduced dynamic orbit determination.
- The reduced-dynamic approach uses both geometric and dynamic information and weighs their relative strength by solving local geometric position corrections using a process noise model to absorb dynamic model errors.
- Launchers or Launch Vehicles is used to carry spacecraft to space. India has two operational launchers: Polar Satellite Launch Vehicle (PSLV) and Geosynchronous Satellite Launch Vehicle (GSLV).
- GSLV with indigenous Cryogenic Upper Stage has enabled the launching up to 2 tonne class of communication satellites. The next variant of GSLV is GSLV Mk III, with indigenous high thrust cryogenic engine and stage, having the capability of launching 4 tonnes class of communication satellites.
- In order to achieve high accuracy in placing satellites into their orbits, a combination of accuracy, efficiency, power and immaculate planning are required.
- ISRO's Launch Vehicle Programme spans numerous centres and employs over 5,000 people. Vikram Sarabhai Space Centre, located in Thiruvananthapuram, is responsible for the design and development of launch vehicles. Liquid Propulsion Systems Centre and ISRO Propulsion Complex, located at Valiamala and Mahendragiri respectively, develop the liquid and cryogenic stages for these launch vehicles.
- Satish Dhawan Space Centre, SHAR, is the space port of India and is responsible for integration of launchers. It houses two operational launch pads from where all GSLV and PSLV flights take place.
Doppler Shift:
Doppler shift in frequency due to relative motion between the satellite and a point on the
Earth surface is the prime concern in the low orbit satellites and has to be taken care for
Establishment of perfect communication link.
Doppler can be given as
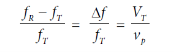
Where ƒR , ƒT are transmitted and received frequencies respectively,
VT is the component of transmitter velocity directed towards the receiver and
Vp is the phase velocity of light.
The Doppler is not available in the downlink, but it affects the uplink if unchecked.
The Doppler is not available with geostationary satellite since there is no relative
Motion between the earth station and the satellite.
Range variations:
With the best station-keeping systems available, the position of a geostationary
Satellite with respect to the earth exhibits cyclic variations daily. The resulting range
Variations has negligible effect on the power equations, an effect on the roundtrip
Delay.
This adds unacceptably large guard times in the TDMA systems. So, the TDMA
System continuously monitors the range and adjusts the burst timing accordingly.
Eclipse
A satellite is said to be in eclipse when the earth blocks the solar energy to solar panels
Of the satellite when the three come in line. The eclipse occurs twice in a year around equinox. The figure shows the eclipse time per day during the period of eclipse.
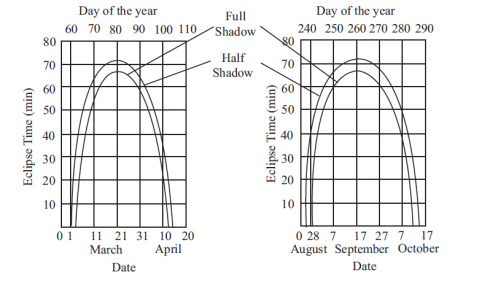
Dates and durations of eclipses
- The solar eclipse caused by moon to the geostationary satellite occurs when the moon moves to front of the sun. The eclipse occurs irregularly in time of duration and depth. In general, the eclipse may occur twice within a 24 hr period.
- Eclipse may range from a few minutes to over two hours within an average duration of about 40 minutes.
- Compared to earth-solar eclipse, the number of moon-solar eclipse range from zero to four with an average of two per year.
- If the moon-solar eclipse of long duration occurs just before or just after the earth-solar eclipse, the satellite has to face special problems in connection with battery recharging and spacecraft thermal reliability. In order to cope with the solar battery problems during eclipses an energy reserve is provided with the satellite.
During full eclipse, a satellite receives no power from sun and operates entirely from batteries. This can reduce the available power significantly, as the spacecraft nears the end of its life,
It may necessitate shutting down some of the transponders during the eclipse period. Spacecraft designers must guard harmful transients as solar power fluctuates sharply at the beginning and end of an eclipse.
There is a possibility of having the primary power failure and so, the probability that a primary power supply failing is much more during eclipse rather than any other operations like deployment.
Sun-transit outage
The overall receiver noise will rise significantly to effect the communications when the sun passes through the beam of an earth station antenna. This effect is predictable and can cause outage for as much as 10 min a day for several days and for about 0.02% an average year. The receiving earth station has to wait until the sun moves out of the main lobe of the antenna. This occurs during the daytime, where the traffic is at its peak and forces the operator to hire some other alternative channels for uninterrupted communication link.
References
- Optical Fiber Communications: Principles and Practice John M Senior
- Optical Fiber Communications by Gerd Keiser.
