1.1 Enhancement MOSFET | unit 1 mosfet and its analysis

MOSFET and its Analysis

1.1 Enhancement MOSFET

Enhancement Type – the transistor requires a Gate-Source voltage, ( VGS ) to switch the device “ON”. The enhancement mode MOSFET is equivalent to a “Normally Open” switch.

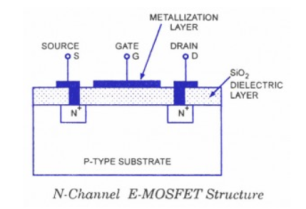
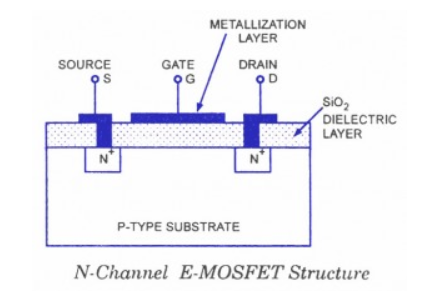
Construction

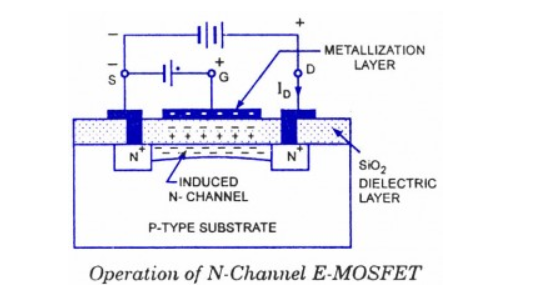
Figure shows the construction of an N-channel E-MOSFET. The main difference between the construction of Depletion -MOSFET and that of Enhancement -MOSFET, as we see from the figures given below the E-MOSFET substrate extends all the way to the silicon dioxide (SiO2) and no channels are doped between the source and the drain. Channels are electrically induced in these MOSFETs, when a positive gate-source voltage VGS is applied to it.

Working

MOSFET operates only in the enhancement mode and has no depletion mode.

It operates with large positive gate voltage only.

It does not conduct when the gate-source voltage VGS = 0. This is the reason that it is called normally-off MOSFET.

In these MOSFET’s drain current ID flows only when VGS exceeds VGST [gate-to-source threshold voltage].

When drain is applied with positive voltage with respect to source and no potential is applied to the gate two N-regions and one P-substrate from two P-N junctions connected back to back with a resistance of the P-substrate.

So,a very small drain current that is, reverse leakage current flows.

If the P-type substrate is now connected to the source terminal, there is zero voltage across the source substrate junction, and the–drain-substrate junction remains reverse biased.

When the gate is made positive with respect to the source and the substrate, negative (i.e. minority) charge carriers within the substrate are attracted to the positive gate and accumulate close to the-surface of the substrate.

As the gate voltage is increased, more and more electrons accumulate under the gate.

Since these electrons cannot flow across the insulated layer of silicon dioxide to the gate, so they accumulate at the surface of the substrate just below the gate.

These accumulated minority charge carriers N -type channel stretching from drain to source.

When this occurs, a channel is induced by forming what is termed an inversion layer (N-type). Now a drain current start flowing.

The strength of the drain current depends upon the channel resistance which, in turn, depends upon the number of charge carriers attracted to the positive gate. Thus, drain current is controlled by the gate potential.

Since the conductivity of the channel is enhanced by the positive bias on the gate so this device is also called the enhancement MOSFET or E- MOSFET.

The minimum value of gate-to-source voltage VGS that is required to form the inversion layer (N-type) is termed the gate-to-source threshold voltage VGST.

For VGS below VGST, the drain current ID = 0. But for VGS exceeding VGST an N-type inversion layer connects the source to drain and the drain current ID is large.

1.1.2 Characteristics

The Drain characteristics of an N-channel E-MOSFET are shown in figure. The lowest curve is the VGST curve.

When VGS is lesser than VGST, ID is approximately zero.

When VGS is greater than VGST, the device turns- on and the drain current ID is controlled by the gate voltage.

The characteristic curves have almost vertical and almost horizontal parts.

The almost vertical components of the curves correspond to the ohmic region, and the horizontal components correspond to the constant current region.

Thus E-MOSFET can be operated in either of these regions i.e. it can be used as a variable-voltage resistor (WR) or as a constant current source.

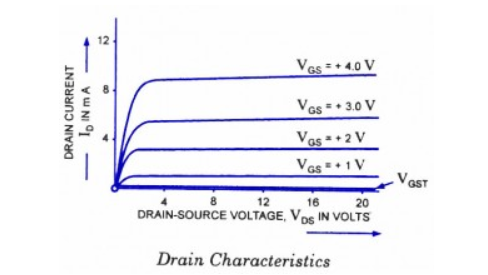
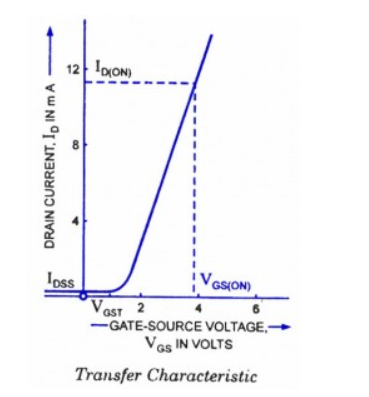
The figure shows the transfer characteristics of E-MOSFET

The current IDSS at VGS <=0 is very small, being of the order of a few nano-amperes.

When the VGS is made positive, the drain current ID increases slowly at first, and then much more rapidly with an increase in VGS.

The manufacturer sometimes indicates the gate-source threshold voltage VGST at which the drain current ID attains some defined small value, say 10 u A.

A current ID 0N, corresponding approximately to the maximum value given on the drain characteristics and the values of VGS required to give this current VGs QN are also usually given on the manufacturers data sheet.

The equation for the transfer characteristic does not obey equation. However it does follow a similar “square law type” of relationship.

The equation for the transfer characteristic of E-MOSFETs is given as:

ID=K(VGS-VGST)2

1.1.3 DC Load line

Assume that the time varying input is sinusoidal. Figure shows the transistor characteristics, dc load line and Q-point where the dc load line and Q-point functions of vGS,VDD,RD and the transistor parameters.

For the output voltage to be a linear function of input voltage, the transistor must biased in saturation region.

The figure shows sinusoidal variations in the gate-to-source voltage, drain current and drain to source voltage as a result of the sinusoidal source. The gate to source voltage is the sum of VGSQ and vi.

As vi increases the instantaneous value of vgs increases and the bias point moves up the load line.

For large value of vgs larger drain current is produced for small value of vDS .

For a negative vi the instantaneous value of vGS decreases below quiescent and the bias point moved down the load line.

Once Q-pt is established a mathematical model is developed for sinusoidal or small signal variations in gate-source voltage , drain to source voltage and drain current.

The time varying signal source vi generates a time-varying component of the gate-to-source voltage.

For FET to operate as linear amplifier the transistor must be biased in saturation region and the instantaneous drain current and drain to source voltage must be confined to the saturation region.

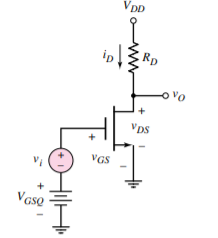
1.1.4 AC equivalent circuit

From the figure we see that the output voltage is

vDS = vo = VDD -iD RD -----------------------------------(1)

Using eq(1) we obtain

vo = VDD – (IDQ +id) RD = (VDD – IDQ RD) - idRD----------------------------(2)

The output voltage is a combination of dc and ac value . The time-varying output is the time-varying drain-to-source voltage or

Vo = vds = -idRD------------------------------------------------------(3)

We know that

id = gm vgs --------------------------------------------------------------------(4)

The equations in terms of instantaneous ac values as well as the phasors are

vgs=vi

Vgs = Vi

And

id = gm vgs

and

vds = -id RD

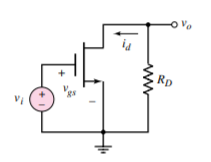
AC equivalent circuit

The ac equivalent in figure is developed by setting the dc sources in figure is equal to zero.

1.1.5 Parameters

The instantaneous gate to source voltage is

vGS= VGSQ + vi = VGSQ + vgs------------------------------------(1)

where VGSQ is the dc component and vgs is the ac component. The instantaneous drain current is

iD = Kn(vGS – VTN) 2-----------------------------------------------------(2)

Substituting (1) in (2) we get

iD= Kn[VGSQ + vgs -VTN ] 2 = Kn [(VGSQ – VTN +vgs] 2---------------------(3a)

iD= Kn[VGSQ -VTN ] 2 +2Kn [(VGSQ – VTN ) vgs + Kn v2 gs ----------------------------(3b)

The first term in (3b) is the dc or quiescent drain current IDQ , The second term is the time-varying drain current component that is linearly related to the signal vgs and the third term is proportional to the square of the signal voltage.

For sinusoidal input signal the squared term produces undesirable harmonics or non-linear distortion in the output voltage.

To minimize these harmonics we require

vgs ≤ 2(VGSQ- VTN )

1.1.6 Parasitic

Due to their structure, MOSFETs have a parasitic capacitance, as indicated in the diagram below. The diagram below is for an example of an N-channel MOSFET, but the situation is much the same for P-channel devices.

In the power MOSFETs we handle large amounts of power, the parasitic capacitance must be regarded as a parameter that limits the usage frequency and switching speed.

The drain and source of a MOSFET are insulated from the gate by the gate oxide film. A PN junction is formed between the drain and source with substrate intervening, and a parasitic ("body") diode is present.

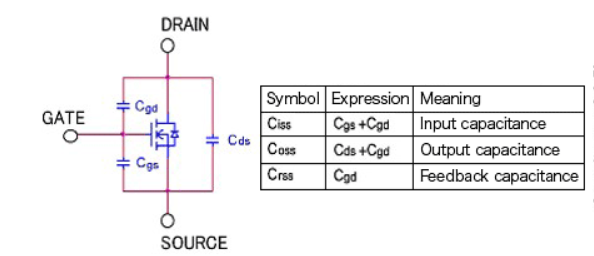
The three parameters Ciss, Coss, Crss appearing on MOSFET data sheets in general relate to these parasitic capacitances.

Ciss is the input capacitance, and is the capacitance obtained by totaling the gate-source capacitance Cgs and the gate-drain capacitance Cgd; it is the capacitance of the MOSFET as a whole, as seen from the input. Qg is the amount of charge necessary to drive (charge) Ciss.

Coss is the output capacitance, obtained by adding the drain-source capacitance Cds and the gate-drain capacitance Cgs, and is the total capacitance on the output side.

If Coss is large, a current arising due to Coss flows at the output even when the gate is turned off, and time is required for the output to turn off completely.

Crss is the gate-drain capacitance Cgditself, and is called the feedback capacitance or the reverse transfer capacitance.

If Crss is large, the rise in drain current is delayed even after the gate is turned on, and the fall in current is delayed after the gate is turned off.

In other words, this parameter greatly affects switching speed. Qgd is the charge amount necessary to drive (charge) Crss.

1.2 Non-ideal characteristics

1.1.6 Finite output resistance:

Due to channel -length modulation the MOSFET drain current is slightly dependent on vDS and thus is defined as

iD = K(vGS – Vt) 2 (1+ 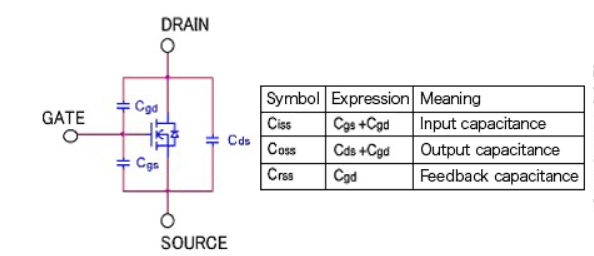vDS)

To determine the relationship between the small signal voltage vgs and small signal current id we can apply small signal analysis of this equation as

id = d iD / d vGS | vGS= VGS

= 2K (vGS – Vt) | VGS = VGS vgs

= 2K (vGS – Vt). Vgs

= gm.vgs

v DS and current iD are related by

id =d iD / d vGS | vGS= VGS .Vds

= K (Vgs – VT) 2 |vGS= VGS .Vds

= v ds / ro

ro = output resistance

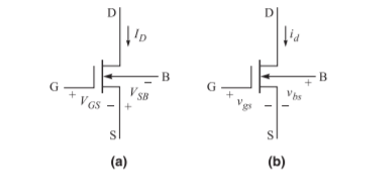
1.1.7 Body effect

The body effect occurs in MOSFET in which the substrate or body is not connected to the source. For an NMOS device the body is connected to the most negative potential in the circuit and will be at signal ground.

The simplified current-voltage relation is

iD = Kn (vGS– VTN )2 and the threshold is given by

VTN = VTNO +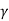 [ 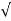2ɸ +vsB - 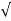2ɸf ]

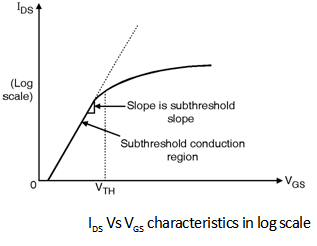
1.1.8 Sub Threshold Construction

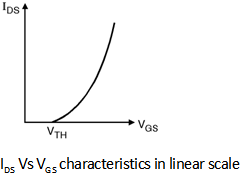
In order to address the subthreshold conduction phenomenon let us plot the

IDS-VGS characteristics shown in Figure below.

A closer inspection of the IDS-VGS curve shows that the current does not drop abruptly to '0' at VGS = VTH.

It indicates that the MOS transistor is partially conducting for voltages below the threshold voltage.

This effect is called as subthreshold or weak inversion conduction.

From the IDS-VGS curve in log scale it is clear that current does not drop to zero immediately for VGS < VTH but actually decays in an exponential fashion.

Thus even VGS < VTH IDS is finite but it exhibits exponential dependence on VGS for smaller values of VDS roughly in the range of 200 mV.

The subthreshold conduction effect can be formulated as :

IDS = I0 exp VGSnKTq

Where n > 1 is a non ideality factor.
• In digital circuit designs the presence of subthreshold current is not desirable because it deviates the transistor from its ideal switch like behaviour which require that current should drop as fast as possible once the gate to source voltage falls below VTH.
• The subthreshold conduction behaviour is represented subthreshold slope factor (S) which indicates the change in VGS for one decaded change in drain current. The unit of S is mV/decade.
• From the above Equation we can show that,
S = n KTq ln (10)

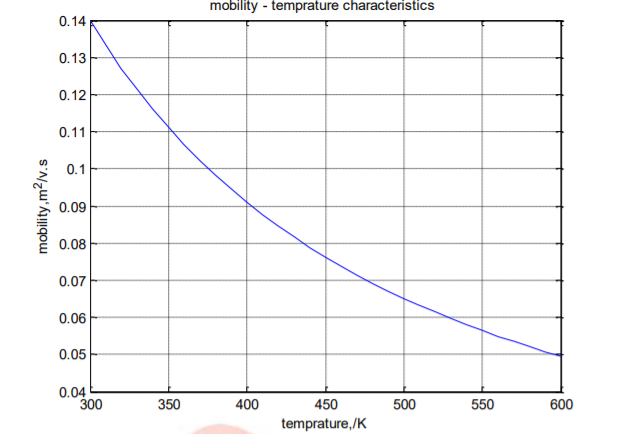
1.2.4 Temperature Effect

In order to capture the dependence of mobility on temperature , doping, and electric field different mathematical models were developed. The carrier mobility is given by

μT = μ (Tr) (T/Tr) k μ

where

T = Absolute temperature

Tr = Room temperature

Kμ = Fitting parameter with a typical value of about 1.5

μ(Tr)= ref temp (300K) = 0.14 m2 / v.s

The analytical modelling of the carrier mobility is shown in figure. It reveals the inverse relationship between temperature and carrier mobility .

1.2.5 Effect of W/L ratio

The K constant specifically Kn is called the conduction parameter of the n-channel device.

Kn is given by:

Kn=k′n/2⋅W/L

Where

k′n=μnCox

μn is the mobility of the electrons in the inversion layer and Cox is the oxide capacitance per unit area.

According to Neamen the k′n parameter is called the "process conduction parameter" and is considered to be a constant for a fabrication technology. Therefore, the ratio W/L is the transistor design variable.

Neamen goes on to say that the design variable is used to design MOSFETS to produce specific current-voltage characteristics in MOSFET circuits.

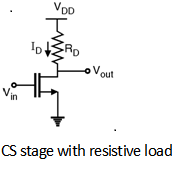
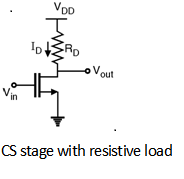
1.2.6 Common Source Amplifier and Analysis

Figure below shows the common source amplifier circuit. In this circuit the MOSFET converts variations in the gate-source voltage into a small signal drain current which passes through a resistive load and generates the amplified voltage across the load resistor.

Now from above Figure,

ID = ½ μ Cox W/L (VGS – VTH )2

That is

ID = ½ μ Cox W/L (Vin – VTH )2

By KVL

VDD – ID RD = Vout

Vout = VDD– ½ μn Cox W/L (Vin – VTH )2RD

Differentiating this equation with respect to Vin

dVout / dVin = - μn Cox W/L (Vin – VTH )RD

Hence the voltage gain Av = -gmRD

Also, from small signal model of shown in above Figure.

By applying KVL,

Vin – VGS = 0

Vin = VGS

Also,

Vout + gmVGSRD =0

Vout = -gmVGS RD

Hence, the voltage gain Av = Vout / Vin – gm RD

As the gate terminal of MOSFET draws a zero current we can say that the common source amplifier provides a current gain of infinity.

Therefore Ai= ∞

Also because of zero gate current the input impedance of CS amplifier is also infinite. Therefore, Rin = ∞

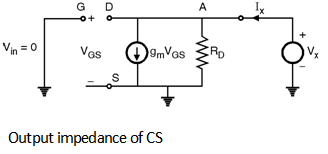
In order to calculate the output impedance Rout consider the circuit shown in
Figure below.

By applying KCL at point 'A'

We get

gmVGS + Vx-0/RD = Ix

But VGS =0

Vx/RD = Ix

Rout = Vx/Ix = RD

Rout = RD

The output impedance of common source amplifier is

Rout = RD

1.2.7 Source Follower

This is the common drain amplifier. This type of amplifier has the input signal fed at the gate similar to the CS amplifier but the signal output is taken at the source terminal as shown in figure.

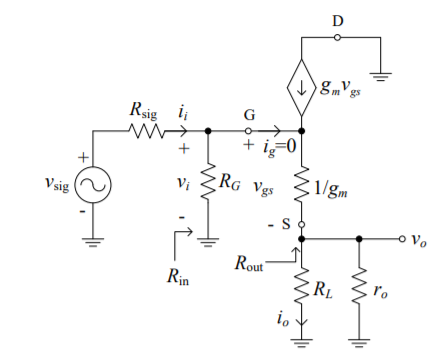
We’ll calculate the following small-signal quantities for this MOSFET common gate amplifier Rin, Av, Avo, Gv, Gi , Ais and Rout. To begin construct the small-signal equivalent circuit:

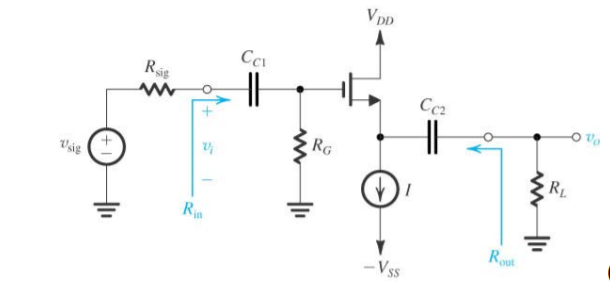
Because the drain terminal is an AC ground, one end of the output resistance ro was shifted so it appears in parallel with RL. This makes the T model suited for amplifier since RL || ro appears series with 1/gm.

Input resistance Rin : With ig =0 the small signal equivalent circuit that

Rin = RG .

Partial small signal voltage gains Av and Avo. At the output side of the small signal circuit with ig=0

vo = gm vgs (RL ||ro )

At the input using voltage division

vgs = 1/gm/ 1/gm + RL ||ro . vi

The small signal partial voltage gain

Av = vo/vi = RL ||ro / RL || ro + 1/gm

Notice that if ro>> RL and RL>> 1/gm then AV< 1

In case of open circuit load (RL ∞) the small-signal partial voltage gain becomes

Avo = Av|RL ->∞ =ro/ ro + 1/gm

Overall small signal voltage gain G . Using voltage division at the input to the small -signal equivalent circuit

vi = Rin / Rin + Rsig. Vsig

Substituting this

Gv = vo/vsig = Vi/vsig. Vo/vi = vi/vsig . Av

The overall small signal voltage gain of this common drain amplifier to be

Gv = vo/vsig = RG/ RG + Rsig . RL ||ro / RL ||ro + 1/gm

If ro>> RL and RL>> 1/gm as well as RG >>Rsig then

Gv< 1

This common drain amplifier is called source follower amplifier.

1.2.8 Comparison with common source

In case of open circuit load (RL  ∞) the small-signal partial voltage gain becomes

Avo = Av|RL ->∞ =ro/ ro + 1/gm

Overall small signal voltage gain G . Using voltage division at the input to the small -signal equivalent circuit

vi = Rin / Rin + Rsig. Vsig

Substituting this

Gv = vo/vsig = Vi/vsig. Vo/vi = vi/vsig . Av

The overall small signal voltage gain of this common drain amplifier to be

Gv = vo/vsig = RG/ RG + Rsig . RL ||ro / RL ||ro + 1/gm

If ro>> RL and RL>> 1/gm as well as RG >>Rsig then

Gv< 1

This common drain amplifier is called source follower amplifier

In order to calculate the output impedance Rout consider the circuit shown in
Figure below.

By applying KCL at point 'A'

We get

gmVGS + Vx-0/RD = Ix

But VGS =0

Vx/RD = Ix

Rout = Vx/Ix = RD

Rout = RD

The output impedance of common source amplifier is

Rout = RD

1.2.9 Frequency response of amplifier

Figure shows the typical frequency response of an amplifier. At low frequencies the output voltage decreases because of coupling and bypass capacitors. At high frequencies, the output voltage decreases because of transistor and stray wiring capacitance.

Critical frequencies:

Where the output voltage is 0.707 of Vmax.
Two critical frequencies -> f1, f2

Midband:

Is the band of frequencies between 10 * f1 and 0.1 * f2.
The midband is where an amplifier is supposed to be operated.

Ex: Find the midband of an amplifier with f1 = 5 Hz and f2 = 100 KHz.

10 * f1 = 10 * 5 Hz = 50 Hz -- > lower end

0.1 * f2 = 0.1 * 100 KHz = 10 KHz -- > upper end

Midband: 50 Hz - 10 KHz

References:

 MOSFET theory and designBook by R. Warner

 Operational Amplifiers - Theory and DesignBook by Johan H. Huijsing

 Fundamentals of Electronics: Book 2: Amplifiers: Analysis and Design Book by Ernest M. Kim and Thomas Schubert