Unit – 1
Linear Differential Equations (LDE) and Applications
The linear homogeneous differential equation of the nth order with constant coefficients can be written as
y(n) (x) + a1y(n-1)(x)+.....+an-1y’(x)+any(x) =0
Where a1 ,a2,......an are constants which may be real or complex.
Using the linear differential operator L (D), this equation can be represented as
L (D) y(x) =0,
Where
L (D) = Dn + a1D(n-1)+⋯+an-1D+an.
Example 1:
Solve the differential equation y’’’+2y’’-y’-2y=0
Solution:
The corresponding characteristic equation is,
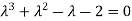
Solving it, we find the roots
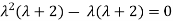
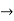
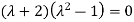

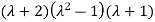 =0
=0
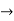
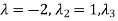 =-1
=-1
The general solution for the differential equation is
Y(x)= 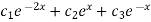
Where 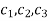 are arbitrary constants.
are arbitrary constants.
Example 2:
Solve the equation y’’’+11y’-5y=0
Solution:
The characteristic equation of the give D.E is
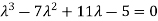
Here one of the root is  then factorising the term
then factorising the term 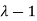 from the equation we obtain
from the equation we obtain
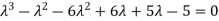
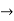 (
(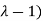 (
(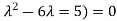
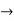 (
( =0
=0
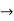 (
(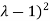 (
(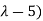 =0
=0
Thus the equation has two roots 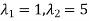
Hence the general equation of the D.E is
Y(x)=(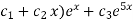
Where 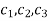 are arbitrary constants.
are arbitrary constants.
Y= C.F + P.I
Example 1:
Determine the complementary function for the following D.E
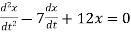 at t=0,1
at t=0,1
Solution:
We can write the given homogeneous equation as follows
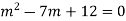
The auxiliary equation is 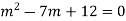
By factorising the auxiliary equations we get,
(m-3)(m-4)=0
And the two real solutions are m=3,4
Hence the complementary function is,
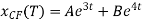
Since f(t) = 2 then 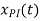 = c
= c
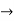 12c=2
12c=2
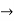 c=1/6 and
c=1/6 and 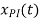 = 1/6
= 1/6
Therefore the general solution is
X(t) = 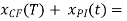
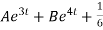
Example 2:
Solve 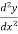 -
-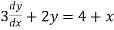
Given y=4 ,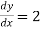 when x=0
when x=0
Solution :
The auxiliary equation is
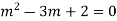
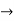 (m-1)(m-2)=0
(m-1)(m-2)=0
 m=1,2
m=1,2
Therefore complimentary function is,
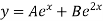
The particular integral is given by y=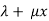

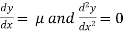
Substituting the above values in given equation we get,
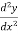 -
-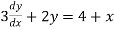 = 0-3
= 0-3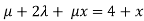
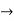 by comparing the co-efficients we get 2
by comparing the co-efficients we get 2 =1
=1 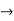
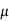 = ½
= ½
 -3
-3 + 2
+ 2 = 4+x
= 4+x
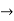
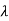 = 11/4
= 11/4
Therefore P.I is,
11/4+(1/2)x
General solution is, y = A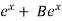 + 11/4 +1/2x
+ 11/4 +1/2x
Example 1:
Solve the following linear equations generally
 9x+2y=6 9x+2y=6
9x+2y=6 9x+2y=6
3x-y=7 6x-2y=14
6x-2y=14
Solving the above two equations we get,
9x+2y=6
 6x-2y=14
6x-2y=14
15x = 20
 x= 20/15 = 4/3
x= 20/15 = 4/3
Example 2:
Short cut methods:
(1) 2x-a+4=x+3a-1
Solution: 2x-x=3a-1+a-4 (-a+4 moves to right side)
 x= 4a – 5
x= 4a – 5
(2) 5x-7=2x+5
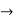 3x = 12
3x = 12  x= 12/3=4
x= 12/3=4
(3) X-m+3=2m+1
Solution: x= 2m+1+m-3= 3m-2 (-m and +3 to right side)
Consider a second order LDE with constant co-efficient given by
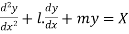
Then let the complimentary function 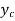 is given by
is given by

Then the particular integral is
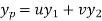
Where u and v are unknown and to be calculated using the formula
u=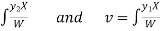
example1 :
find the particular integral for the following
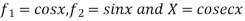
Solution:
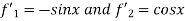
Now the C.F is as follow,
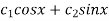

We find u and v accordingly
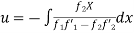
= -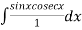 = -x
= -x
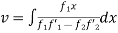
=  = log(sinx)
= log(sinx)
P.I = 
= -xcosx +log(sinx)
The general solution is y = C.F +P.I
Y = 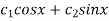 -xcosx +log(sinx)
-xcosx +log(sinx)
Example 2:
Wronskain ,W= 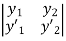
= 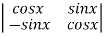 =
= 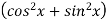 =1
=1
Particular integral is given by,
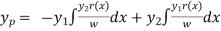
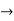
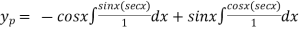 secx= 1/cosx
secx= 1/cosx
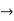
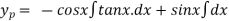
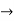

The general solution is,
Y = C.F +P.I
Y = 
Cauchy’s theorem:
Statement:
Let f(x) and g(x) be continuous on an interval [a,b],differentiable on(a,b), and g’(x)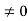 for all x
for all x (a,b).then thereexists a point x=c in this interval such that
(a,b).then thereexists a point x=c in this interval such that
Proof:
First of all we must note that  0
0
We consider an auxiliary equation
F(x) = f(x) + 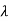 g(x)
g(x)
And we choose 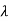 in such a way to satisfy the condition F(a) = F(b). In this case we get,
in such a way to satisfy the condition F(a) = F(b). In this case we get,
f(a) + 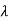 g(a) = f(b) +
g(a) = f(b) + 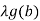 ,
,
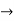 f(b) – f(a) =
f(b) – f(a) = 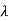 [g(b)-g(a)
[g(b)-g(a)
Then the function F(x) takes,
F(x) = f(x)- 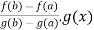
Example 1:
Check the validity for cauchy’s mean value theorem f(x) = 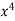 and g(x) =
and g(x) = 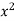 on the interval [1,2]
on the interval [1,2]
Solution:
The derivatives of this function are,
f’(x) = (x4) = 4x3, g’(x)=(x2) = 2x
substituting in the Cauchy formula we get,
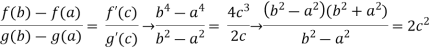
We take into account that the boundaries of the segment are a=1 and b=2
C=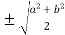
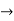 c=
c=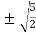 =
=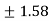
Example 2:
Check the validity for cauchy’s theorem for the function f(x) = x2 and g(x) = arc tanx on the interval [0,1]
Solution:
At first we calculate the derivatives of the given function
f’(x) = (x3)’ , g’(x) = (arctanx)’= 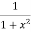
substitute f(x),g(x) and their derivatives in the Cauchy formula
 =
= 

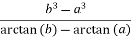 =
= 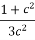
For the values of a=0, b=1 we obtain,
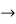
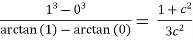

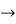
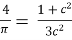
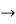 12c2 =
12c2 = 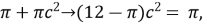
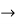
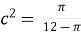
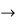 c =
c = 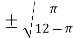
Given we consider the segment [0,1],we choose the positive value for c which lies in interval(0,1)
C=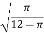
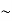
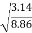
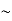 0.60
0.60
Legendre’s formula:
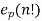 =
= 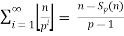
Where p is a prime and 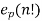 is the exponent of p in the prime factorization of n! And sp(n) is the sum of the digits of n when written in bas p
is the exponent of p in the prime factorization of n! And sp(n) is the sum of the digits of n when written in bas p
Example:
Using the first form of Legendre’s equation , substitute the values in the formula
The values are n=27 and p =2
Solution :
Consider the legendre’s formula,
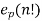 =
= 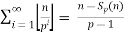
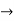 substituting the given values in the formula we get,
substituting the given values in the formula we get,
 =
=  =
= 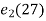 =
= 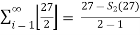 = 27 – s2(27)
= 27 – s2(27)
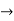 the number 27 when expressed in the base 2 gives rise to 11011.this gives us,
the number 27 when expressed in the base 2 gives rise to 11011.this gives us,
s2(27) = 1+1+0+1+1 = 4

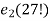 = 27 – s2(27) = 27 – 4 =23
= 27 – s2(27) = 27 – 4 =23
Which means that the larget integer k for which 2k divides 27! Is 23.
Example 1:

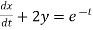 ....(2)
....(2)
Solve the given simultaneous differential equations
Solution:
Consider the given equations
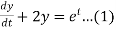
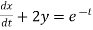 ....(2)
....(2)
Consider eq(1),(2)
Dx+2y = et ....(1)
Dx +2x =e-t....(2)
Eliminating ‘x’ from both the equations we get,
1 2
2 2Dx + 2y = 2et
2Dx + 2y = 2et

 D
D  2Dx +D2y = e-t
2Dx +D2y = e-t

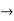 y = Ae2t + Be-2t +
y = Ae2t + Be-2t + 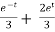
Example 2:
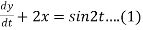

Given that x(0)=1 and y(0)= 0
Solution:
Consider the given equations,
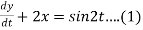
 Dy +2x = sin2t
Dy +2x = sin2t
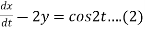
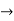 Dx -2y = cos2t
Dx -2y = cos2t
By solving the above equations we get,
(D2 +4)Y =0
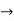
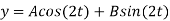
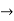
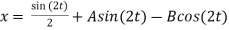
X(0) = 1, y(0) = 0
 A =0, B=-1
A =0, B=-1


Introduction
In “real-world,” there are many physical quantities that can be represented by functions. Involving only one of the four variables e.g., (x, y, z, t). Equations involving highest order derivatives of order one = 1st order differential equations. Examples Function σ(x) = the stress in a uni – axial stretched tapered metal rod .
Function v(x) =the velocity of fluid flowing a straight channel with varying cross-section.
Solution Method of First Order ODEs Solution of Linear (Homogeneous Equation)
Typical form of the equation
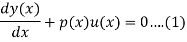
The solution u(x) in eq(1) is given by,
U(x) =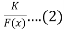
Where k= constant to be determined by given condition and the function F(x) has the form:
F(x)= 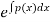 ...(3)
...(3)
In which p(x) is given in differential equation.
Type 2
Solution Method of First Order ODEs Solution of Linear (Non-Homogeneous Equation)
Typical form of the equation
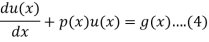
The appearance of g(x) in eq(4) tends to non-homogenous
The solution u(x) in eq(4) is given by,
U(x) =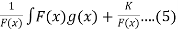
Where k= constant to be determined by given condition and the function F(x) has the form:
F(x)= 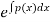
Some important terms to be considered to solve the electrical circuit problems:
*If a current i(t) is flowing through a resistor R ohms, then the voltage 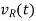 across
across
*the resistor is given by 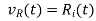
*for an inductor of L Hentry, the voltage-current relationship is given by
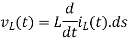
*For a capacity of c farad,the voltage current relation ship is given by
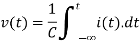
Example:
Finding the optimal current of an electrical circuit(RL circuits) in which the initial
Condition is i=0 at t=0
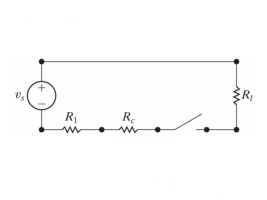
Solution:
By Kirchhoff voltage law(KVL) method, we get
The differential equation for the RL circuit will be 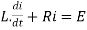
In which initial conditions are i=0 at t=0
The standard form of the equation is,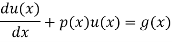
Dividing the differential equation by L to obtain
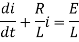
The integrating factor is

Multiplying the above equation with standard form gives rise to
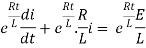
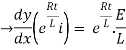
By applying integration on both sides we get

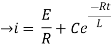
Now applying i=0 at t-0 gives us
0=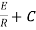
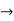 C=-
C=-
NOW
i=
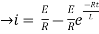
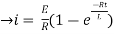 = t
= t 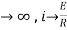
Therefore by finding current of the RL circuits is i=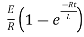
Hence we complete the solution by first order differential equation of first order and even several types of networking circuits and fluid mechanics uses this method.
Example 2:
Resistors of R1= 10Ω, R2 = 4Ω and R3 = 8Ω are connected up to two batteries (of negligible resistance) as shown. Find the current through each resistor.
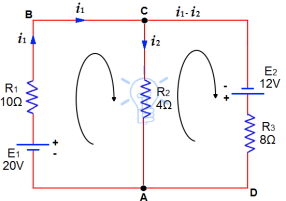
Solution:
Assume currents to flow in directions indicated by arrows
Apply KCL on junctions C and A
Therefore, current in mesh ABC = i1
Current in Mesh CA = i2
Then current in mesh is = i1 - i2
Now, apply KVL on mesh ABC,20V are acting in clockwise direction, equating the sum of IR products, we get
10i1 +4i2 = 20.....(1)
In mesh ACD 12 volts are acting in clock-wise direction, then
8( i1 - i2)-4i2 = 12
 8 i1 - 8 i2-4i2 = 12
8 i1 - 8 i2-4i2 = 12
 8 i1 - 12 i2 = 12...(2)
8 i1 - 12 i2 = 12...(2)
Multiplying eq(1) by 3 we get
30 i1 + 12 i2 = 60
By solving equation 1 and 2 we get,
38i1 = 72
The above equation can be also simplified by elimination or cramer’s rule
I1 = 72/38 = 1.895 Amperes = current in 10 ohms resistor
Substituting this value in (1) we get,
10(1.895)+4i2 = 20
4i2 = 20-18.95
I2 = 0.263 Amperes=current in 4 ohms resistors
Now ,
i1 - i2 = 1.895-0.263=1.632 Amperes
Reference Books
1. Erwin Kreyszig, “Advanced Engineering Mathematics”, Wiley India,10th Edition.
2. M.D. Greenberg, “Advanced Engineering Mathematics”, Pearson Education, 2 nd Edition.
3. Peter. V and O‟Neil, “Advanced Engineering Mathematics”, Cengage Learning,7th Edition.
4. S.L. Ross, “Differential Equations”, Wiley India, 3rd Edition.
5. S. C. Chapra and R. P. Canale, “Numerical Methods for Engineers”, McGraw-Hill, 7th Edition.
6. J. W. Brown and R. V. Churchill, “Complex Variables and Applications”, McGraw-Hill Inc, 8th Edition.