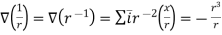Unit – 4
Vector Differential Calculus
The derivative of R(t) with respect to t is given by
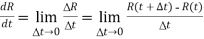
if the limit exists. If
R(t) = x(t) i + y(t) j + z(t) k
Then
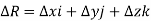
So

Consequently,

Thus
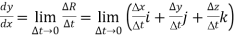
We define a new operator ∇ by
∇=i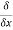 + j
+ j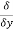 + k
+ k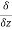
Example 1:
Find the gradient of the following
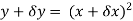
= 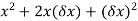


 y=
y=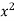
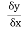 =
= 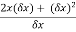 .
.
= 2x+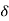
Example 2:
Consider the surface z= 10-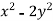 at (1,-1,7), find a 3d tangent vector that points in the direction of steepest ascent.
at (1,-1,7), find a 3d tangent vector that points in the direction of steepest ascent.
Solution:
Let our tangent vector be v= ai+bj+ck.
To find v , we have that,
The direction of steepest ascent of z(x,y) is given by the two-dimensional vector 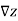 .
.
First we find the x,y components of v,then we find z component of v
Finding x,y components of v,
As the gradient provides the direction of steepest ascent, we compute it:
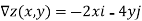
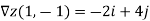
Thus, a=-2 and b=4, and are seeking a tangent vector
V=-2i+4j+ck.
Example 1:
Compute 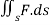 where F= (3x+
where F= (3x+ and s is the surface of the box such that 0
and s is the surface of the box such that 0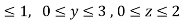 use outward normal n
use outward normal n
Solution:
Writing the given vector fields in a suitable manner for finding divergence
div F =3+2y+x
we use the divergence theorem to convert the surface integral into a triple integral
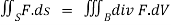
Where B is the box 0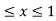 , 0
, 0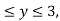
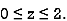
We compute the triple integral of div F=3+2y+x over the box B
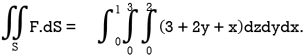
=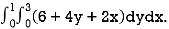
=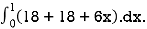
= 36+3=39
Example 2:
For F= (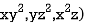 use divergence theorem to evaluate
use divergence theorem to evaluate  where s is the dphere of radius 3 centred at origin.
where s is the dphere of radius 3 centred at origin.
Solution:
Since div F= 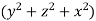 , the surface integral is equal to the triple integral.
, the surface integral is equal to the triple integral.
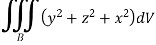
To evaluate the triple integral we can change value of variables to spherical co-ordinates,
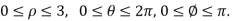
The integral is  =
=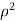 .For spherical co-ordinates, we know that the jacobian determinant is dV =
.For spherical co-ordinates, we know that the jacobian determinant is dV = 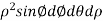 .therefore, the integral is
.therefore, the integral is
 =
= 
= 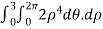
=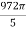
Example: 3
Find the curl of F(x,y,z) = 3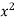 i+2zj-xk
i+2zj-xk
Curl F = 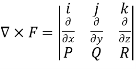
=
=  i -
i - 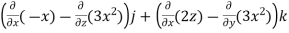
= (0-2)i-(-1-0)j+(0-0)k
= -2i+j
Example:4
What is the curl of the vector field F= ( x +y +z ,x-y-z,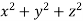 )?
)?
Solution:
Curl F = 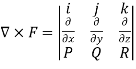
= 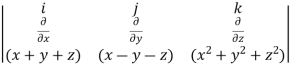
=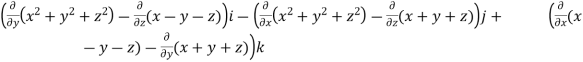
= (2y+1)i-(2x-1)j+(1-1)k
= (2y+1)i+(1-2x)j+0k
= (2y+1, 1-2x,0)
Example:5
Find the curl of F = ( )i +4zj +
)i +4zj +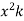
Solution:
Curl F=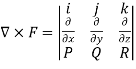
= 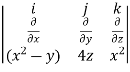
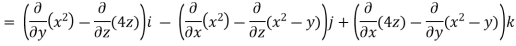
=(0-4)i-(2x-0)j+(0+1)k
=(-4)i – (2x)j+1k
=(-4,-2x,1)
Example 6:
Determine 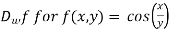 in the direction of
in the direction of 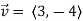
Solution:
First we calculate gradient of the points,
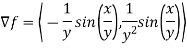
Here we require a unit vector but by our knowledge it is clear that the given vector is not so we change it into unit vector,
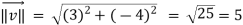
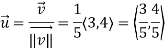

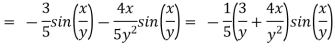
Solenoidal vector formula: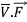 = 0
= 0
Ir-rotattional vector formula: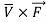 =0
=0
Example: 1
Show that  = yz
= yz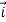 +zx
+zx +xy
+xy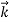
Solution:
 = yz
= yz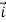 +zx
+zx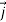 +xy
+xy
To prove : 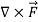 =0
=0
 =
= 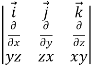
= 0
Example:2
Prove 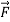 =(
=(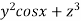 )
)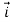 +(2ysinx-4)
+(2ysinx-4)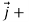 3x
3x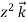 is irrotational and find its scalar potential.
is irrotational and find its scalar potential.
Solution:
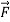 =(
=(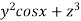 )
)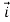 +(2ysinx-4)
+(2ysinx-4)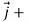 3x
3x
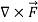 =
=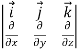
= 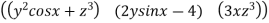
Hence,  is irrotational
is irrotational
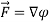
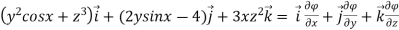
Equating the co-efficient of 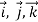 we get,
we get,
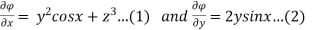
Example1:
Determine the vector field 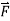 (x,y) =
(x,y) =  is conservative or not
is conservative or not
Solution:
Note that the domain 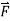 is the part of R2 in which y>0.Thus, the domain of
is the part of R2 in which y>0.Thus, the domain of 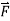 is part of a plane above the x-axis and this domain is simply connected (there are no holes in this region and this region is connected).Therefore, we can use the cross-partial property of conservative fields to
is part of a plane above the x-axis and this domain is simply connected (there are no holes in this region and this region is connected).Therefore, we can use the cross-partial property of conservative fields to
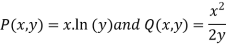
Then 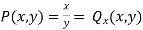 and thus
and thus 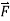 is conservative.
is conservative.
Example 2:
Test for conservative
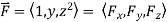
Solution:
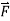 is conservative if
is conservative if 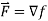
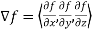
Where 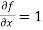
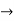 f(x,y,z) = x+g(y,z)
f(x,y,z) = x+g(y,z)
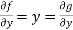
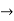
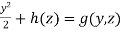
∂f/∂z=∂h/∂z=z^2→h(z)=z^3/3+c
→ f(x,y,z) = x + y^2/2+z^3/3+c
∴ F ⃑=∇f hence F ⃑ is conservative.
Example 1:
F(x,y) = 2i + 3j is a conservative vector field.Find a potential function for it.
Solution:
Note : As F(x,y) is conservative,it has a potential function.That is,there is some function ∅(x,y) such that F(x,y)= ∇∅(x,y).
The function ∅(x,y) can be found by integrating each component of
F(x,y)
To find potential function we consider,
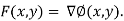
2i +3j = 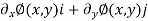
Thus ,
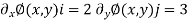
By integrating we get,
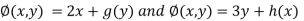
By combining the above equation we get a possible potential function for

Example 2:
If F (x,y) = 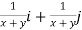 is conservative? If so ,find a
is conservative? If so ,find a  such that
such that
F(x,y) = 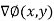
Solution:
The vector field F(x,y) = u(x,y)i+v(x,y)j is conservative if and only if
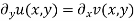
We identify(x,y) =  ,from which we can compute the partial derivatives
,from which we can compute the partial derivatives


They are equal so they are conservative.
Finding the potential 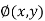
As we proved for conservative now we find the potential function.
Therefore the function 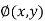 can be determined by integrating the equations from each component of
can be determined by integrating the equations from each component of
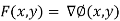 =
=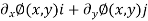
And combining the results into a single function  we get,
we get,
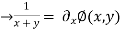 ....(1)
....(1)

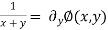 .....(2)
.....(2)
Integrating (1) w.r.to x and (2) w.r.to y
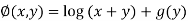
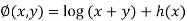 , for any g(y) and h(x)
, for any g(y) and h(x)
These both relations are satisfied by
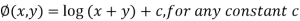
Some vector identities are as follows:
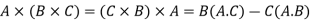
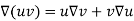
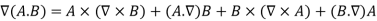
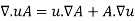
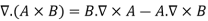
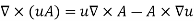

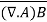
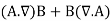
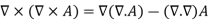
Example 1:
Show that d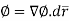
Solution:
Let 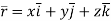 , then
, then 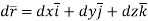
If 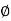 is any scalar point function, then
is any scalar point function, then
d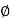 =
= 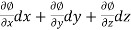
= 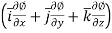 .
.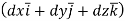
= 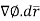
Example 2:
If r=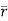 where
where 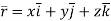
Then show that ,
(1)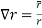
(2)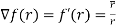
(3)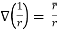
Solution:
Given 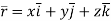 and r=
and r=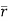
i.e. 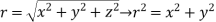 +
+
differentiate w.r.to x partially we get,
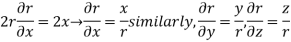
(1)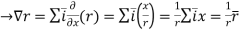
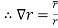
(2)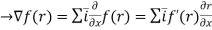
=f’(r)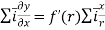 = f’(r).
= f’(r).
(3) )
)