Unit – 5
Vector Integral Calculus & Applications
Let- F be vector function defined throughout some region of space and let C be any curve in that region. ṝis the position vector of a point p (x,y,z) on C then the integral ƪ F .dṝ is called the line integral of F taken over
Now, since ṝ =xi+ yi+ zk
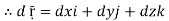
And if
F͞ =F1i + F2 j+ F3 K

Q1. Evaluate 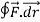 where F= cos y.i-x siny j and C is the curve y=
where F= cos y.i-x siny j and C is the curve y=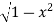 in the xy plae from (1,0) to (0,1)
in the xy plae from (1,0) to (0,1)
Solution : The curve y=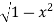 i.e x2+y2 =1. Is a circle with centre at the origin and radius unity.
i.e x2+y2 =1. Is a circle with centre at the origin and radius unity.
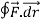 =
= 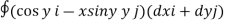
= 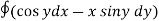
=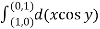 =-1
=-1
Q2. Evaluate 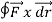 where
where 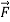 = (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).
= (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).
Solution : F x dr = 
Put x=t, y=t2, z= t3
Dx=dt ,dy=2tdt, dz=3t2dt.
F x dr = 
=(3t4-6t8) dti – ( 6t5+3t8 -3t7) dt j +( 4t4+2t7-t2)dt k
=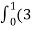 t4-6t3)dti –(6t5+3t8-3t7)dt j+(4t4 + 2t7 – t2)dt k
t4-6t3)dti –(6t5+3t8-3t7)dt j+(4t4 + 2t7 – t2)dt k
=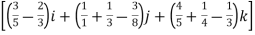
=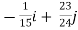 +
+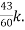
Sums Based on Line Integral
1. Evaluate 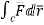 where
where 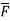 =yz i+zx j+xy k and C is the position of the curve.
=yz i+zx j+xy k and C is the position of the curve.
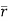 = (a cost)i+(b sint)j+ct k , from y=0 to t=π/4.
= (a cost)i+(b sint)j+ct k , from y=0 to t=π/4.
Soln. 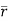 = (a cost)i+(b sint)j+ct k
= (a cost)i+(b sint)j+ct k
The parametric eqn. of the curve are x= a cost, y=b sint, z=ct (i)
 =
=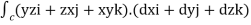
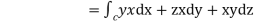
Putting values of x,y,z from (i),
dx=-a sint
dy=b cost
dz=c dt
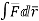 =
=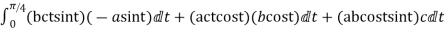
=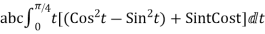

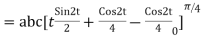
= =
= 
2. Find the circulation of 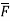 around the curve C where
around the curve C where 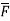 =yi+zj+xk and C is circle
=yi+zj+xk and C is circle 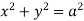 .
.
Soln. Parametric eqn of circle are:
x=a cos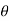
y=a sin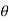
z=0
 =xi+yj+zk = a cos
=xi+yj+zk = a cos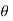 i + b cos
i + b cos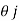 + 0 k
+ 0 k
d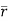 =(-a sin
=(-a sin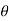 i + a cos
i + a cos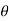 j)d
j)d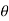
Circulation =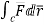 =
=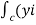 +zj+xk). d
+zj+xk). d
=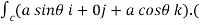 -a sin
-a sin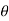 i + a cos
i + a cos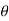 j)d
j)d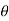
=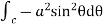 =
= 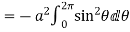
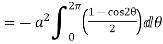

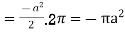
Example 1:
Given a plane z= 3x+4y+2 that lies above the rectangle [0,5]  [1,4]. Find the surface area
[1,4]. Find the surface area
Solution:
The area of the surface with equation z=f(x,y),(x,y) D ,where
D ,where 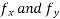 are continuous,
are continuous,
Is A(S)= 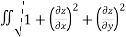 dA
dA
We have z=2+3x+4y.
Then,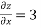 and
and 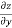 =4
=4
A(S) =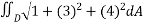
From the dimensions of the rectangle, we get the limits of x as (0,5) and the limits of y as(1,4)
On substituting the known values in the expression for area ,we get
A(S) =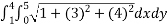
Evaluate the iterated integral.
A(S) =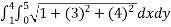
=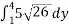
=15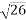
Example 2:
As an example, let us consider the following integral in two dimensions:
I=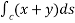
Where C is a straight line from the origin to (1,1), as shown the figure ,Let s be the arc length measured from the origin .We then have
x =s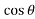 =
=
y=s sin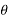 =
=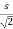
The endpoint (1,1) corresponds to s=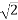 .Thus , the line integral becomes
.Thus , the line integral becomes
I=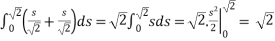
Q1. Find the work done in moving a particle once round the complete circle x2+y2=a2 , z=0 in the force filed given by 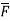 = sin yi +(x + x cos y )j.
= sin yi +(x + x cos y )j.
Solution: work done=  =
=  (x+x cos y )dy
(x+x cos y )dy
Using parametric equation x=a cos θ, y=a sinθ
Work done =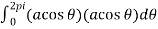
= 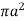 .
.
Q 2:What is the work done by force of gravity.
Solution:
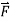 =
= 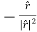
Since the radius is not specified we will use the variable R for radius.
We know the vector equation for a circle 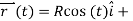 Rsin(t)
Rsin(t) 
We are given F in terms of r
We have the work equation 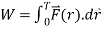
We know that T =2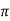 becayse that is one rotation of a circle
becayse that is one rotation of a circle
Putting everthing together we get the equation

Lets break down each component
Simplify 
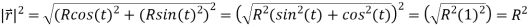
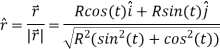
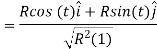
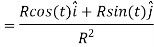

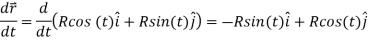
R is a constant so we can just move that out and substitute in our results for 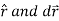
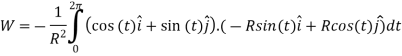
The equation can just be solved using integrals,
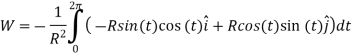
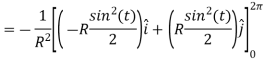
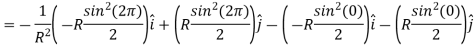
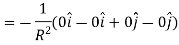
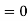
Example 3:
Prove that ͞͞͞F = [y2 cos x +z3] i+(2y sin x – 4) j +(3xz2 + 2) k is a conservative field. Find (i) scalar potential for͞͞͞F (ii) the work done in moving an object in this field from (0, 1, -1) to (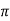 / 2,-1, 2)
/ 2,-1, 2)
 Sol. : (a) The fleld is conservative if cur͞͞͞͞͞͞F = 0.
Sol. : (a) The fleld is conservative if cur͞͞͞͞͞͞F = 0.
 Now, curl͞͞͞F =
Now, curl͞͞͞F = 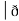 ̷̷
̷̷ X
X 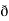 /
/ 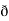 y
y 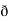 /
/ 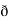 z
z
Y2COS X +Z3 2y sin x-4 3xz2 + 2
; Cur 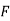 = (0-0) – (3z2 – 3z2) j + (2y cos x- 2y cos x) k = 0
= (0-0) – (3z2 – 3z2) j + (2y cos x- 2y cos x) k = 0
; F is conservative.
(b) Since F is conservative there exists a scalar potential ȸ such that
F = ȸ
 (y2 cos x=z3) i + (2y sin x-4) j + (3xz2 + 2) k =
(y2 cos x=z3) i + (2y sin x-4) j + (3xz2 + 2) k = 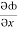 i +
i + 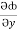 j +
j + 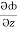 k
k
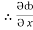 = y2 cos x + z3,
= y2 cos x + z3, 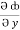 = 2y sin x – 4,
= 2y sin x – 4, 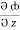 = 3xz2 + 2
= 3xz2 + 2
Now, 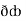 =
= 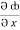 dx +
dx +  dy +
dy + 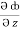 dz
dz
= (y2 cos x + z3) dx +(2y sin x – 4)dy + (3xz2 + 2)dz
= (y2 cos x dx + 2y sin x dy) +(z3dx +3xz2dz) +(- 4 dy) + (2 dz)
=d(y2 sin x + z3x – 4y -2z)
 ȸ = y2 sin x +z3x – 4y -2z
ȸ = y2 sin x +z3x – 4y -2z
(c) now, work done =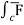 .d ͞r
.d ͞r
= 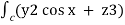 dx + (2y sin x – 4) dy + ( 3xz2 + 2) dz
dx + (2y sin x – 4) dy + ( 3xz2 + 2) dz
=  (y2 sin x + z3x – 4y + 2z) (as shown above)
(y2 sin x + z3x – 4y + 2z) (as shown above)
= [ y2 sin x + z3x – 4y + 2z ](  /2, -1, 2)
/2, -1, 2)
= [ 1 +8  + 4 + 4 ] – { - 4 – 2} =4
+ 4 + 4 ] – { - 4 – 2} =4 + 15
+ 15
If P and Q are two functions of x, y and their partial derivatives 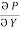 ,
,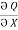 are continuous single valued functions over the closed region bounded by a curve C then
are continuous single valued functions over the closed region bounded by a curve C then
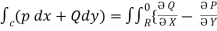 } dx dy.
} dx dy.
EXAMPLE – 1 :
Verify green’s theorem for 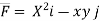 and C is the triangle having verticles A (0,2 ) , B (2,0 ) , C (4,2 ).
and C is the triangle having verticles A (0,2 ) , B (2,0 ) , C (4,2 ).
SOLUTION : By green theorem.
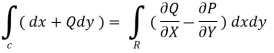
Here,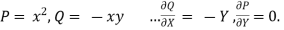
(a) Along AB, since the equation of AB is
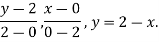
Putting 
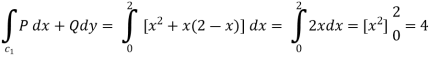
Along BC , since the equation of BC , 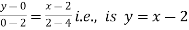 .
.
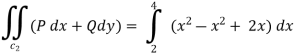
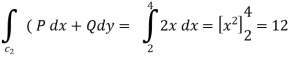
Along CA , since the equation of CA, is y = 2 , dy = 0.
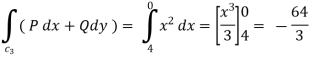

(b) 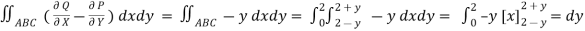
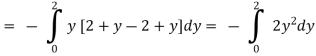
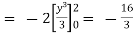 .
.
From (1) and (2) , the theorem is verified .
Example 2 :
Evaluate by Green ‘s theorem 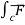 = - xy (xi –yj) and c is r= a (1+ cos
= - xy (xi –yj) and c is r= a (1+ cos 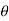 )
)
Sol : By Green’s Theorem , 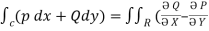 ) dx dy
) dx dy
Now, 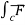 .dṝ =
.dṝ = 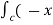 2yi + xy2 j ) . (d xi + dy j) =
2yi + xy2 j ) . (d xi + dy j) = 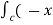 2y dx + xy2dy )
2y dx + xy2dy )
By comparison p= - x2y, Q = xy2
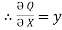 2,
2, 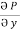 = - x2
= - x2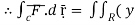 2 + x2) dx dy
2 + x2) dx dy
To evaluate the integral , we put x = r cos 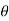 , y = r sin
, y = r sin 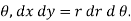 for the cardioid r = a ( 1 + cos
for the cardioid r = a ( 1 + cos 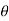 ), we take the integral from
), we take the integral from 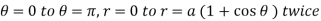
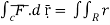 2 .rdr d
2 .rdr d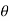 = 2
= 2 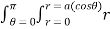 3dr d
3dr d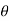
= 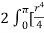 ]a ( 1 + cos
]a ( 1 + cos  ) dθ =
) dθ = 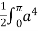 (1+ cos θ)4dθ
(1+ cos θ)4dθ
=8a4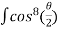 =
=  a4
a4
Example Based on Green’s Theorem
example 1:
Verify Green’s Theorem in the plane for 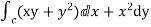
Where c is theclosed curve of region bounded by y=x and y= .
.
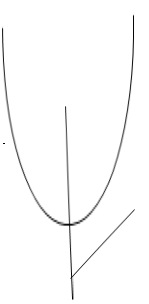
Soln: By Green’s Theorem,
 A(1,1)
A(1,1)
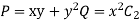 y=x
y=x y=
y=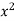
 B
B
(a) Along 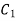 , y=
, y= and dy=2x dx and x varies from 0 to 1.
and dy=2x dx and x varies from 0 to 1.
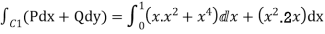
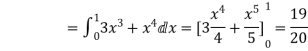
 Along
Along  y=x and dy=dx and x varies from 1 to 0.
y=x and dy=dx and x varies from 1 to 0.
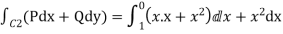
=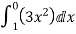
=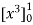 = 1
= 1
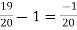 = L.H.S.
= L.H.S.
RHS=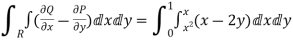
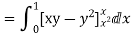
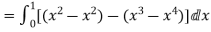
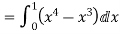
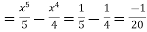
Example 2:
Use Green’s theorem to evaluate 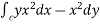 .
.
To Green’s theorem to evaluate the integral we have,
P=
Then the Green’s theorem integral become,
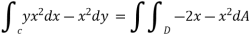
Finding the values of D in polar form
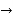
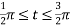 and
and 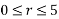
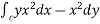 =
= 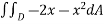
= 
= 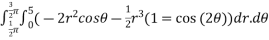
=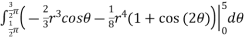
=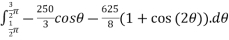
= 
= 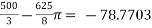
The integral of the normal component of the curl of a vector F͞ over a surface S is equal to the line integral of the tangential component of F͞ around the curve bounding S i.e
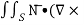 F͞ )ds =
F͞ )ds =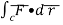
Q1.Use stoke’s theorem to evaluate 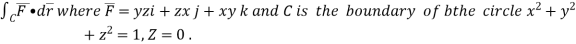
SOLUTION : We have by stoke’s theorem 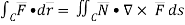
Now ,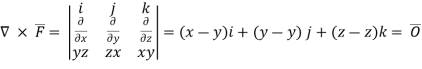
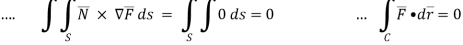
Example 2:
For F(x,y,z)=(y,z,x) compute 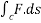
Solution:
Since we are given a line integral and need to apply a stroke’s theorem,we compute surface integral
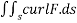
Where s is a surface with boundary c,we can choose any surface s,as long as we are oriented it so that c is a positively oriented boundary.
We need to calculate curl F using the notation
Curl F = 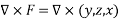
= 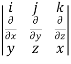
=i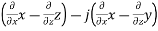 +
+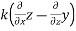
=i(-1)-j(1)+k(-1)
=(-1,-1,-1)
Next we calculate surface by,
 for 0
for 0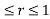 and 0
and 0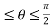
Now we calculate the normal vector n:


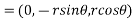
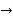
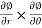 =i(r
=i(r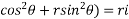
To orient the surface properly we must use the normal vector 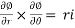
At this point we can already see that the integral 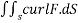 should be positive.The vector field curl F=(-1,-1,-1) and the normal vector (-r,0,0) are pointing in similar direction.
should be positive.The vector field curl F=(-1,-1,-1) and the normal vector (-r,0,0) are pointing in similar direction.
Now we compute the all pieces of the integral,
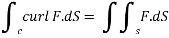
= 

 example3:
example3:

Soln: We have Gauss Divergence Theorem
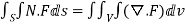
By data, F=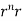

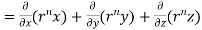


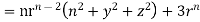
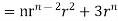
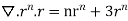
=(n+3)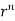

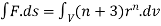
Example 4:
Prove that 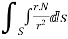 =
=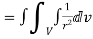
Soln. By Gauss Divergence Theorem,
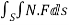 =
=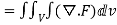
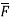 =
=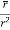 =
=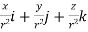
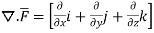 .[
.[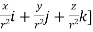

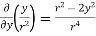
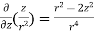
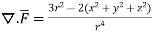 =
= 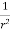
Example 1:
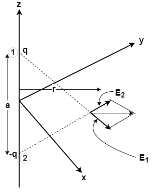
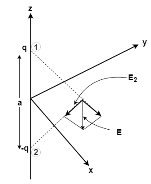
Two point charges are a distance a part along the z-axis as shown is below diagram.Find the electric field at any point in the z=0, plane when the charges are:
(a) both equal to q
(b) of opposite polarity but equal magnitude 
solution:
(a) In the plane z=0 plane ,each point charge alone gives rise to field components in the ir and ix directions. When both charges are equal ,
The superposition of field components due to both charges cancel in the z
direction but add rapidly:
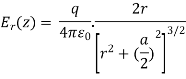
As a check, note that far away from the point charges 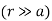 the field approaches that of a point charge of value 2q:
the field approaches that of a point charge of value 2q:
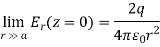
(b) When the charges have opposite polarity,the total electric fied due to both charges now cancel in the radical direction but add in the z-direction:
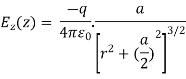
Far away from the point charges the electric field dies off as the inverse cube of distance :
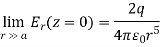
The following diagram explains us clearly regarding the two-point charges:
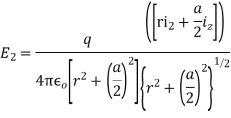

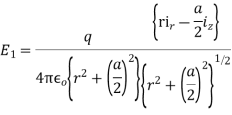
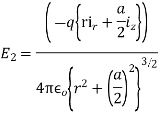
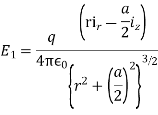
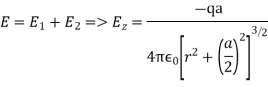
Example 2:
An infinitely long uniformly distributed line charge 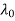 along the z-axis is shown in the below figure. consider the two symmetrically located charge
along the z-axis is shown in the below figure. consider the two symmetrically located charge 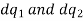 a distance z above and below point p, a radical distance r away.Each charge element alone contributes radical z components to electric field.however,just as we have in two charge elements to-gether cause equal magnitude but oppositely directed z field components that cancel leaving only additive radical components:
a distance z above and below point p, a radical distance r away.Each charge element alone contributes radical z components to electric field.however,just as we have in two charge elements to-gether cause equal magnitude but oppositely directed z field components that cancel leaving only additive radical components:
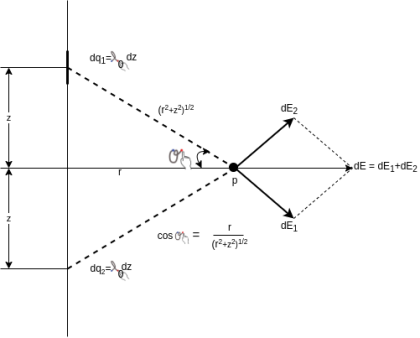
Solution:
We have,
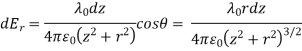
To find the total electric field we integrate over the length of the line charge:
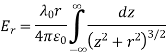
= 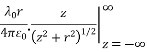
= 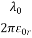
Reference Books:
1. Erwin Kreyszig, “Advanced Engineering Mathematics”, Wiley India,10th Edition.
2. M.D. Greenberg, “Advanced Engineering Mathematics”, Pearson Education, 2 nd Edition.
3. Peter. V and O‟Neil, “Advanced Engineering Mathematics”, Cengage Learning,7th Edition.
4. S.L. Ross, “Differential Equations”, Wiley India, 3rd Edition.
5. S. C. Chapra and R. P. Canale, “Numerical Methods for Engineers”, McGraw-Hill, 7th Edition.
6. J. W. Brown and R. V. Churchill, “Complex Variables and Applications”, McGraw-Hill Inc, 8th Edition.