Unit 2
Time domain analysis
For a second order control system, the total time response is analysed by its transient as well as ready state response.
 Any system which contains energy along elements (L1 c etc) if suffer any disturbance in the energy state effect at the input end as at this output or at both the ends takes source time to change in thus form one state other. This change its then is called as Transient times and the values of reverent and voltage during this period is Transient Response.
Any system which contains energy along elements (L1 c etc) if suffer any disturbance in the energy state effect at the input end as at this output or at both the ends takes source time to change in thus form one state other. This change its then is called as Transient times and the values of reverent and voltage during this period is Transient Response.

Fig:1 Transient Response
The above fig: a clearly shows steady state response is that part of response when the transient has died. If the steady star response of the output does not match with input then the system has steady state errors.
Consider the following open loop system –
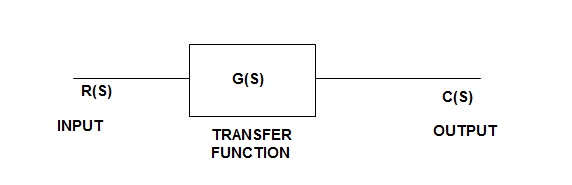
Fig 2 Open loop system block diagram
L-1[c(s)] = L-1[ G(s) R (S)]
C(t) = L-1[ G(S) Q (s)]
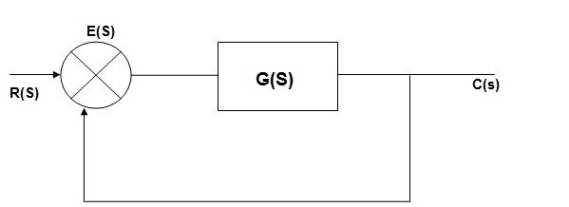
Fig 3 Closed loop system block diagram
E(s) = R(s) –c(s) [ error signal]
C(S)= [ R(s)- c(Q)] G(s)
C(s) = R(s) G(s)- c(s) G(s)
C(s) [ 1+G(s)] = R(s) G(s)
C(s)/R(s) = G(s)/1+G(s)
C(s)/R(s) = G(s)/1+G(s)
E(s) = R(s)- c(s)
=R(s)-R(s) G(s)/1+G (s0
E(s) = R(s) [1/1+G(s)
If no error then E(s) = 0, f(t) = 0 Hence, r(t) = c(t)
Key takeaway
The error signal is the difference between the unity feedback signal and input signal.
The Impulse signal, Ramp signal, unit step and parabolic signals are used as the standard test signals. All these signals are explained below.
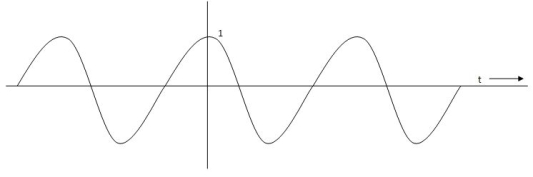
Impulse Signal: -
This signal has zero amplitude everywhere except at the origin. Fig below shown the representation of Impulse signal.

Fig 4 Unit Impulse Signal
The mathematical representations
A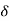 (t) = 0 for t ≠0
(t) = 0 for t ≠0
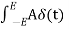 dt = A e
dt = A e 
Where A represent energy or area of the Laplace Transform of Impulse signal is
L [A (t)] = A
(t)] = A
UNIT IMPULSE SIGNAL: -
If A = 1
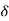 (t) = 0 for t ≠0
(t) = 0 for t ≠0
L [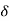 (t)] = 1
(t)] = 1
The transfer function of a linear time invariant
System is the Laplace transform of the impulse response of the system. If a unit impulse signal is applied to system then Laplace transform of the output c(s) is the transfer function G(s)
As we know G(s) = c(s)/R(S)
r(t) = 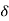 (t)
(t)
R(s) = L [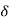 (t)] = 1
(t)] = 1
:. G(S) = C(s)
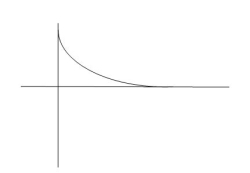
(b) Step signal: -
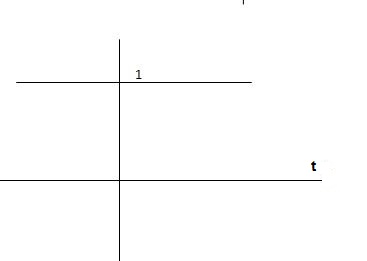
Step signal of size A is a signal that change from zero level to A in zero time and stays there forever.
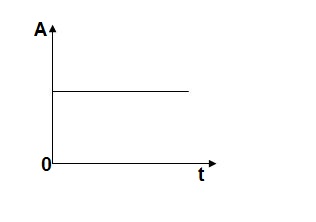
Fig 5 Unit Step Signal
r(t)= A t >=0
=0 t<0
L[r(t)] = R(s) = A/s
UNIT STEP SIGNAL: - If the magnitude of the slip signal is I then it is called unit step signal.
u(t) = 1
t>=0
t<0
L[u(t)] = 1/s
(c) Ramp Signal: -
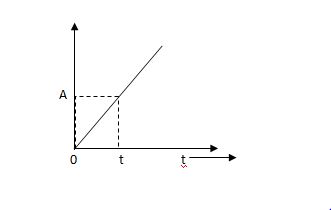 The vamp signal increase linearly with time from initial value of zero at t= 0 as shown in fig is below
The vamp signal increase linearly with time from initial value of zero at t= 0 as shown in fig is below
Fig 6 Ramp Signal
r(t) = At t>=0
=0 t<0
A is the slope of the line The Laplace transform of ramp signal is
L[r(t)] = R(s) = A/s2
(d) Parabolic Signal: -
The instantaneous value of a parabolic signal varies as square of the time from an initial value of zero t=0. The signal representation in fig 14 below.
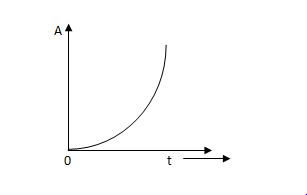
Fig 7 Parabolic Signal
r(t) At2 t>=0
=0 t<0
Then Laplace Transform is given as
R(s) = L[At2] = 2A/s3
If no error then E(t) =0, :. R(t) = c(t), output is tracking the input.
Steady state Errors signal (ess): - (t 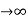 )
)
Ess = t 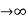 e(t)
e(t)
Using final values, the theorem
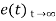 = ess =
= ess = 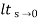 S.E (s)
S.E (s)
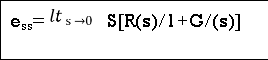
Key takeaway
If no error then E(t) =0, :. R(t) = c(t), output is tracking the input.
Steady state Errors signal (ess): - (t 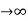 )
)
Ess = t 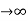 e(t)
e(t)
Using final values, the theorem
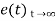 = ess =
= ess = 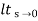 S.E (s)
S.E (s)
The order of the system is defined as the maximum power of S in the denominator. The type of system is defined as the number of poles at the origin.
For example, G(s)= K/S(S+1)
It is order 2 and type 1 system
G(S)= K(S+1)/S2(S+2)
It is order 3 and type 2 system
Key takeaway
The type and order of system is not dependent on the number of zeros.
2.4.1 Transient Analysis of First Order System:
OLTF G(s) = 1/TS
CLTF c(s)/R(s) = 1/1+TS
CE: HTS = 0
S= -1/T
C(s) = R(s) [G(S)/1+G(s)]
C(s) = R(s)/1+TS
So, Calculating value of c(s), c(t) for different input
a) Unit Step:
R(t) = u(t)
R(s) = 1/s
C(s) = 1/s(1+ST)
1/s(1+ST) = A/s + o/1+TS
1/s(1+ST) = A/S + 0/1+TS
1= A(1+ST) + BS
AT +B =0
A = 1
B= -T
C(s) = 1/s + (-T)/1+TS
= 1+ (-T)/1-(-T)s = 1-I/n/1+ass+1/T =e-t/s
 C(t) = [ 1-e-t/T]
C(t) = [ 1-e-t/T]
Fig 8 Output response for Unit Step input
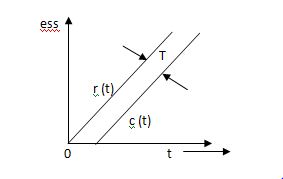
Ramp:
R(t) = t
R(s) = 1/s2
C(s) = R(s) [G(s)/1+G(s)]
C(s) = 1/s2 1/(1+TS) + c
1/s2 (1+TS) = A/(s) + B/s2 + c(1+TS)
1 = A (s+s2. T) + B(1+TS) +cs2
TA +c = 0
A+TB =0
B =1
A = -T
C = T2
C(s) = -T/s + 1/s2 +T2/1+ST
=(-T) u(t) + t(u) + T e-t/T u(t)
= [ -T + t +Te-t/T u(t)
= [ -T+ t+Te-t/T] u(t)
C(s) = t- T+ Te-t/T
ess = 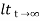 R(t) – c(t)
R(t) – c(t)
= 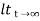 [ t- t+ 7-Te –t/T]
[ t- t+ 7-Te –t/T]
=  T(1-e-t/T]
T(1-e-t/T]
 ess = The less the value of T the less in the errors.
ess = The less the value of T the less in the errors.
Fig 9 Output response for ramp input
Key takeaway
1) From both the Cases input unit step, ramp Unit step
Unit Step Ramp
c(t) = 1-e-t/T r(t) = t
ess = e-t/T (r/t)-(t) c(t) = t- T+te-t/T
ess= e-t/T (r/t) (t) ess = T- Te-t/T
For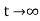 :- for
:- for :-
:-
ess =0 ess = T
2) In both the vases (values of T) must be as small as possible (so, that e-t/T) must be as small as possible which gives us
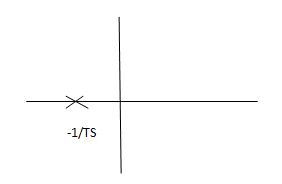
Fig 10 Location of poles
G(s) = 1/Ts
ATf = 1/1+TS
1st order system
Poles must be situated as far as possible from origin i.e. deeper and deeper into the left half of s-place. Thus, we get less errors.
2.4.2 Transient Analysis of Second Order System:
OLTF G(s) = k/s(1+TS)
CLTFC(s)/R(s) = k/k+s(1+Ts)
= k/s2+ s/T +k/T
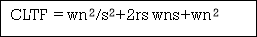 Comparing above equation with standard 2nd order eqn
Comparing above equation with standard 2nd order eqn
Standard 2nd order equation
CEs2+2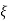 wn s+wn2= 0
wn s+wn2= 0
S= -2 wn±
wn±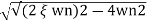 /2
/2
=2 wn±2wn
wn±2wn /2
/2
S=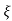 wn±wn
wn±wn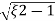
S= -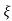 wn±wn
wn±wn
S= -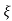 wn ±wn
wn ±wn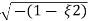
S= - wn ±gwn
wn ±gwn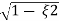
Standard eqn:-
T(s) = wn2/s2+2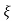 wns+wn2
wns+wn2
Our eqn T(s) = K/T/s2+1/T s+ K/T
Wn2 = k/T
2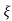 wn = 1/T
wn = 1/T
2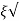 k/T = 1/T
k/T = 1/T
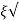 k/T = 1/2T
k/T = 1/2T
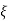 = 1/2T
= 1/2T 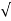 T/K
T/K
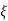 = 1
= 1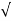 2KT
2KT
Graphically showing the position of loops s1, s2 for offered of
As the characteristic Equn (location of poles) is dependent only on (wn constant for a given system)
S1 = - wn + jwn
wn + jwn  1-
1-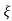 2
2
S2= -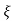 wn - jwn
wn - jwn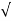 1-
1-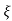 2
2
CASE 1: (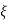 =0)
=0)
S1=jwn, S2, = -jwn
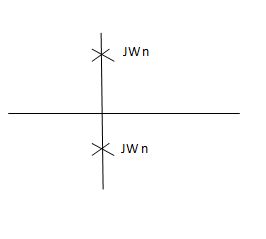
Fig 11 Location of poles for  =0
=0
Undamped
CASE 2:(0< <1)
<1)
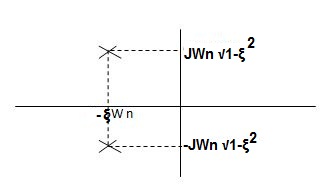
S1= -wn + jwn  0.75
0.75
=-wn/2 +jwn(0.26)
S2 = -wn/2 – jwn (0.86)
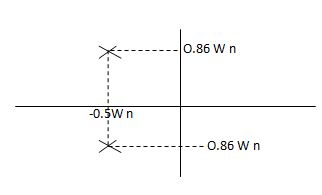
Fig 12 Location of poles for  <1
<1
CASE:3 ( =1)
=1)
S1= S2 = - wn = -wn
wn = -wn

Fig 13 Location of poles for  =1
=1
CASE4: ( =-2)
=-2)
S1 = -2wn +jwn  -3
-3
=-2wn – jwn (1.73)
S1 = -3.73wn
S2 = -2wn –jwn  -3
-3
= -2wn + jwn (1.73)
= -0.27  wn
wn
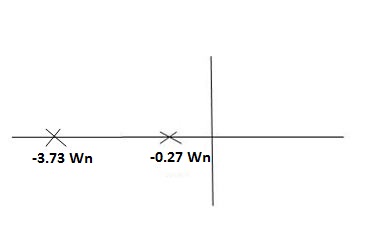
Fig 14 Location of poles for  >1
>1
Overdamped
Key takeaway
All practical systems are 2 order to, if R(e) =  (t) R(s) = 1 :. CLTF = 2nd order st eqn and hence already the system is possible.
(t) R(s) = 1 :. CLTF = 2nd order st eqn and hence already the system is possible.
CLTF = e(s)/ R(s) = wn2/s2+2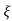 wns+wn2
wns+wn2
Now calculating c(s), c(t) for different values of input
1) Impulse I/p
R(t) = 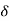 (t)
(t)
R(s) = 1
C(s) = R(s) wn2/s2+2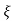 wns+wn2
wns+wn2
C(s) = wn2/s2 +2 wn+wn2
wn+wn2
Under this i/p (R(t) =  (t)) the output varies with different values of
(t)) the output varies with different values of 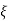 . So,
. So,
CONDITION 1: (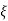 =0)
=0)
C(s) =wn2/s2 +wn2
Os2 +wn2 =0
S=+-jwn
C(t) = wn sinwnt
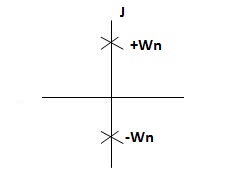
Sinwnt
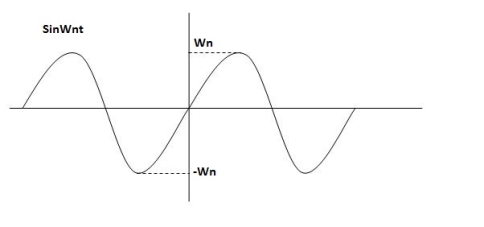
Fig 15 Undamped oscillations
As there in no damping i.e. oscillations at t= 0 are some at t  so, called UNDAMPED
so, called UNDAMPED
CONDITION 2: 0<<1
c(s) = R(s) wn2/s22 wn+wn2 R(t) =
wn+wn2 R(t) = 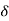 (t)
(t)
R(s) =1
C(s) = wn2/s2+2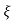 wns+wn2
wns+wn2
CE
S2+2 wns +wn2 =0
wns +wn2 =0
S2, S1 = -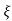 wn ±jwn
wn ±jwn 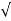 1-
1-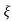 2
2
C(t) = e-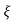 wnt sin( wn
wnt sin( wn 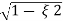 )t
)t
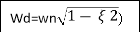
C(t)=e-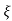 wnt sin (wdt)
wnt sin (wdt)
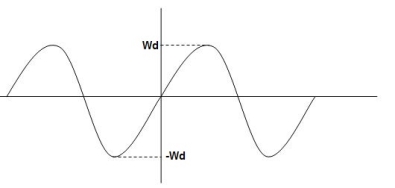

Fig 16 Underdamped oscillations
The oscillations are present but at t- infinity the Oscillations are 0 so, it is UNDERDAMPED
CONDITION 3: =1
=1
C(s) = R(s) wn2/s2+2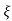 wns+wn2
wns+wn2
C(s)=wn2/S2 +2wns+wn2
=wn2/(s +wn)2
CE S= -Wn
Diagram
C(t)=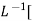 w2n /(
w2n /(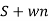 )2
)2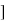
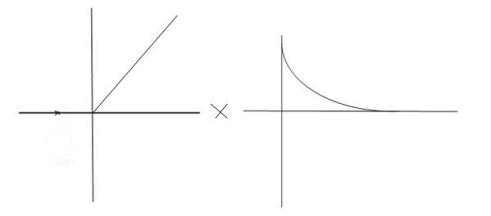 C(t)=
C(t)=
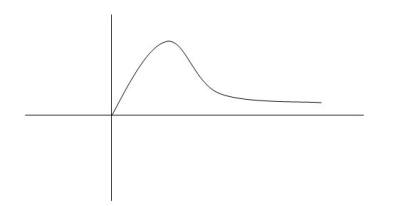
Fig 17 Critically damped oscillations
No damping obtained at 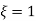 so is called CRITICALLY DAMPED.
so is called CRITICALLY DAMPED.
CONDITIONS 4: >1
>1
C(s) = wn2/s22 wnS+Wn2
wnS+Wn2
S1, s2 = 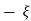 WN+-jwn
WN+-jwn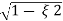
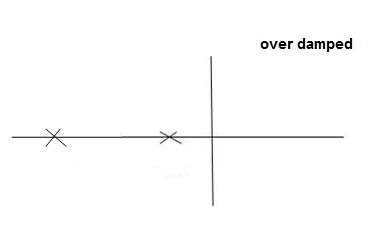
Fig 18 location of poles for over damped oscillations
b) UNIT Step Input:
R(s) = 1/s
C(s)/R(s) = wn2/s2+2 wns+wn2
wns+wn2
C(s) = R(s) wn2 /s2 +2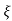 wns+wn2
wns+wn2
C(s) = R(s) wn2/s2+2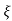 wns+wn2
wns+wn2
C(s) = R(s) wn2/s2+2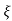 wns+wn2
wns+wn2
C(s) = wn2s(s2+2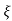 wns+wn2)
wns+wn2)
C(t) = 1- e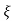 wnt/
wnt/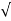 1-es2 sin (wdt + ø)
1-es2 sin (wdt + ø)
Wd = wn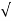 1-
1-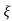 2
2
Ø= 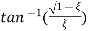
Where
Wd = Damping frequency of oscillations
Wn = natural frequency of oscillations
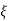 wn = damping coefficient.
wn = damping coefficient.
T= Time constant
Condition 1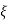 = 0
= 0
C(s) = wn2 /s(s2+wn2)
C(t) = 1- e° sin wdt +ø
C(t)= 1- sin(wn +90)
C(t) = 1+cos wnt
Constant
C(t) = 1+constant
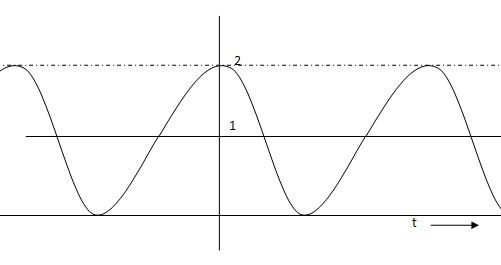
Fig 19 C(t) = 1+cos wnt
Condition 2: 0<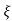 <1
<1
C(s) = 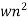 /s2+
/s2+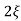 wns +wn2
wns +wn2
C(s) =1/s – s+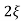 wn/s2+
wn/s2+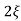 wns +wn2
wns +wn2
=1/s – s+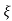 wn/(s+
wn/(s+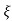 wn)2+wd2-
wn)2+wd2- 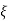 wn/(s+
wn/(s+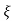 wn2) +wd2
wn2) +wd2
Wd = wn 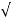 1-
1-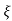 2
2
Taking Laplace inverse of above equation
L --1 s+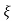 wn/(s+
wn/(s+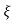 wn) +wd2= e-
wn) +wd2= e-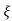 wnt cos wdt
wnt cos wdt
L-1 s+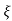 wn/(s+
wn/(s+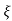 wn)2+wd2 = e-
wn)2+wd2 = e-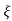 wnt sinWdt
wnt sinWdt
C(t) = 1-e-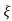 wnt [coswdt +
wnt [coswdt +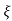 /
/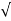 1-
1-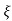 2 sinwdt]
2 sinwdt]
= 1-e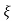 wnt /
wnt /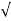 1-
1-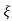 2 sin [wdt +
2 sin [wdt + 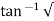 1-
1-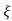 2/
2/ ] t>=0
] t>=0
C(t) = 1-e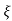 wnt/
wnt/ 1-
1- 2 sin(wdt+ø)
2 sin(wdt+ø)
Ø = 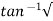 1+
1+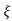 2/
2/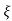
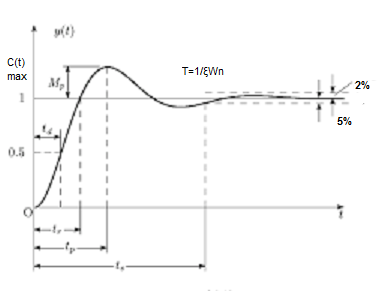
Fig 20. Transient Response of second order system
Specifications:
1) Rise Time (tp): The time taken by the output to reach the already status value for the first time is known as Rise time.
C(t) = 1-e-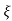 wnt/
wnt/ 1-
1- 2 sin (wdt+ø)
2 sin (wdt+ø)
Sin (wd +ø) = 0
Wdt +ø = n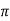
tr = n -ø/wd
-ø/wd
For first time so, n=1.
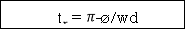
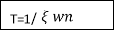
2) Peak Time (tp)
The peak value attained by the output is called peak time. The time required by the output to reach this value is lp.
d(cct) /dt = 0 (maxima)
d(t)/dt = peak value
tp = n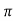 /wd for n=1
/wd for n=1
tp = 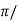 wd
wd
3) Peak Overshoot Value:
Maximum deviation of output from steady state value is called peak overshoot value (Mp).
(ltp) = 1 = Mp
(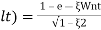 Sin(Wat + φ )
Sin(Wat + φ )
(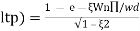 Sin( Wd∏/Wd + φ)
Sin( Wd∏/Wd + φ)
Mp = e-∏ξ / √1 –ξ2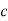
Condition 3 ξ = 1
C( S ) = R( S ) Wn2 / S2 + 2ξWnS + Wn2
C( S ) = Wn2 / S(S2 + 2WnS + Wn2) [ R(S) = 1/S ]
C( S ) = Wn2 / S( S2 + Wn2 )
C( t ) = 1 – e-Wnt + tWne-Wnt
The response is critically damped.
(4). Settling Time (ts) :
ts = 3 / ξWn ( 5% )
ts = 4 / ξWn ( 2% )
Key takeaway
Rise Time tr = 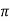 -ø/wd
-ø/wd
Peak Time tp = n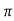 /wd for n=1
/wd for n=1
tp = 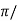 wd
wd
Peak Overshoot Value
Mp% = e-∏ξ / √1 –ξ2
Settling Time
ts = 3 / ξWn ( 5% )
ts = 4 / ξWn ( 2% )
Q.1. The open loop transfer function of a system with unity feedback gain G( S ) = 20 / S2 + 5S + 4. Determine the ξ, Mp, tr, tp.
Soln : Finding closed loop transfer function,
C( S ) / R( S ) = G( S ) / 1 + G( S ) + H( S )
As it is unity feedback so, H(S) = 1
C(S)/R(S) = G(S)/1 + G(S)
= 20/S2 + 5S + 4/1 + 20/S2 + 5S + 4
C(S)/R(S) = 20/S2 + 5S + 24
Standard equation for second order system,
S2 + 2ξWnS + Wn2 = 0
We have,
S2 + 5S + 24 = 0
Wn2 = 24
Wn = 4.89 rad/sec
2ξWn = 5
(a). ξ = 5/2 x 4.89 = 0.511
(b). Mp% = e-∏ξ / √1 –ξ2 x 100
= e-∏ x 0.511 / √1 – (0.511)2 x 100
Mp% = 15.4%
(c). tr = ∏ - φ / Wd
φ = tan-1√1 – ξ2 / ξ
φ= tan-1√1 – (0.511)2 / (0.511)
φ = 1.03 rad.
tr = ∏ - 1.03/Wd
Wd = Wn√1 – ξ2
= 4.89 √1 – (0.511)2
Wd = 4.20 rad/sec
tr = ∏ - 1.03/4.20
tr = 502.34 msec
(d). tp = ∏/4.20 = 747.9 msec
Q.2. A second order system has Wn = 5 rad/sec and is ξ = 0.7 subjected to unit step input. Find (i) closed loop transfer function. (ii) Peak time (iii) Rise time (iv) Settling time (v) Peak overshoot.
Soln: The closed loop transfer function is
C(S)/R(S) = Wn2 / S2 + 2ξWnS + Wn2
= (5)2 / S2 + 2 x 0.7 x S + (5)2
C(S)/R(S) = 25 / S2 + 7s + 25
(ii). tp = ∏ / Wd
Wd = Wn√1 - ξ2
= 5√1 – (0.7)2
= 3.571 sec
(iii). tr = ∏ - φ/Wd
φ= tan-1√1 – ξ2 / ξ = 0.795 rad
tr = ∏ - 0.795 / 3.571
tr = 0.657 sec
(iv). For 2% settling time
ts = 4 / ξWn = 4 / 0.7 x 5
ts = 1.143 sec
(v). Mp = e-∏ξ / √1 –ξ2 x 100
Mp = 4.59%
Q.3. The open loop transfer function of a unity feedback control system is given by
G(S) = K/S(1 + ST)
Calculate the value by which k should be multiplied so that damping ratio is increased from 0.2 to 0.4?
Soln: C(S)/R(S) = G(S) / 1 + G(S)H(S) H(S) = 1
C(S)/R(S) = K/S(1 + ST) / 1 + K/S(1 + ST)
C(S)/R(S) = K/S(1 + ST) + K
C(S)/R(S) = K/T / S2 + S/T + K/T
For second order system,
S2 + 2ξWnS + Wn2
2ξWn = 1/T
ξ = 1/2WnT
Wn2 = K/T
Wn =√K/T
ξ = 1 / 2√K/T T
ξ = 1 / 2 √KT
Forξ1 = 0.2, for ξ2 = 0.4
ξ1 = 1 / 2 √K1T
ξ2 = 1 / 2 √K2T
ξ1/ ξ2 = √K2/K1
K2/K1 = (0.2/0.4)2
K2/K1 = 1 / 4
K1 = 4K2
Q.4. Consider the transfer function C(S)/R(S) = Wn2 / S2 + 2ξWnS + Wn2
Find ξ, Wn so that the system responds to a step input with 5% overshoot and settling time of 4 sec?
Soln:
Mp = 5% = 0.05
Mp = e-∏ξ / √1 –ξ2
0.05 = e-∏ξ / √1 –ξ2
Cn 0.05 = - ∏ξ / √1 –ξ2
-2.99 = - ∏ξ / √1 –ξ2
8.97(1 – ξ2) = ξ2∏2
0.91 – 0.91 ξ2 = ξ2
0.91 = 1.91 ξ2
ξ2 = 0.69
(ii). ts = 4/ ξWn
4 = 4/ ξWn
Wn = 1/ ξ = 1/ 0.69
Wn = 1.45 rad/sec
Please refer section 2.4 it is already covered.
So, for difficult input, ess will be different Input still be
1) R(s) = unit step
2) R (s) = Ramp
3) R(s) = parabolic
1) R(s)= Unit step
R(t) = u(t)
R(s) = 1/s
Ess = 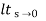 s[ R(s)/1+G(s)]
s[ R(s)/1+G(s)]
= 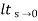 s[ys/1+G(s)]
s[ys/1+G(s)]
ess= 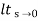 1+1/1+G(s)
1+1/1+G(s)
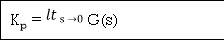 =1/1+lt G(s) s- 0
=1/1+lt G(s) s- 0
(Position error coefficient)

1) R(s) = Ramp
R(t) = t
R(s) = 1/s2
ess= 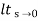 s[ R(s)/1+G(s)]
s[ R(s)/1+G(s)]
= 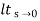 s[ys2/1+G(s)]
s[ys2/1+G(s)]
= 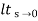 1/s(1+G(S)
1/s(1+G(S)
=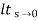 1/s+SG(s)
1/s+SG(s)
ess =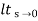 l/s-0 SG (s)
l/s-0 SG (s)
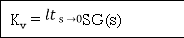 ess =
ess = 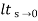 t L/SG (s)
t L/SG (s)
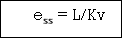 velocity errors coefficient
velocity errors coefficient
(3) Parabolic
R(t) = t2
R(s) =1/s3
Ess = 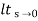 s[ R(s)/1+G(s)]
s[ R(s)/1+G(s)]
= 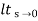 s(1/s3)/1+G(s)
s(1/s3)/1+G(s)
= 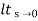 1/s2+s2G(s)
1/s2+s2G(s)
 Ess =
Ess = 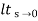 1/s2G(s)
1/s2G(s)
Acceleration error coefficient
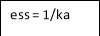
I/p error coefficient
(1) Unit step ess= 1/1+kv kv = 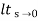 G(S)
G(S)
(2) Ramp ess= 1/kv kv = 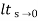 sG(s)
sG(s)
(3) Parabolic ess = 1/ka ka =  s2 G(s)
s2 G(s)
Now finding errors in type 0,1,2 system
1) Type 0:-
G(s) = 1/(s+a) (s+b)
2) Kp :
Kp =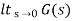
=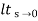 1/(s+a)(s+b)
1/(s+a)(s+b)
Kp= 1/ab
Ess=1/1+np = 1/1+(1/ab) 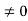
o/p not locking the input
(b) kv:-
Kv = 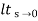 s G(s)
s G(s)
= 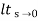 s/(s+a) (s+b)
s/(s+a) (s+b)
=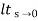 s/(s+a) (s+b)
s/(s+a) (s+b)
Kv = 0
ess = 1/kv = 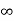
o/p not locating the input
(3)ka:-
Ka = 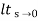 s2 G(s)
s2 G(s)
=  s2 /(s+a) (s+b)
s2 /(s+a) (s+b)
Ka =0
ess = 1/ka = 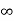
o/p not locking the input
(2)Type –I :-
G(s) = 1/s(s+a) (s+b)
(a)Kp:-
Kp = 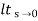 G(s)
G(s)
=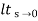 1/s(s2+as+ab)
1/s(s2+as+ab)
Kp = 1/0 = 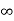
ess = 1/1+kp = 0
o/p is tracking the input
(b)kv:-
Kv = 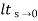 S G(s)
S G(s)
=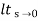 1/(s+a) (s+b)
1/(s+a) (s+b)
=1/ab
Kv = 1/ab
ess =1/ka = ab 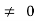
o/p is not tracking the input
3)ka :
Ka= 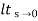 s2G(s)
s2G(s)
= 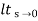 s2 /s(s+a)(s+b)
s2 /s(s+a)(s+b)
= 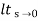 s/(s+a)(s+b)
s/(s+a)(s+b)
Ka= 0
Ess = 1/ka = 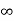
O/p is not tracking the input.
3) Type 2:
G(s) = 1+/(s2(s+a) (s+b)
a) Kp:-
Kp =  G(s)
G(s)
=  1/s2 (s+a) (s+b)
1/s2 (s+a) (s+b)
Kp = 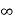
ess = 1/1+kp = 0
o/p tracking the i/p
b) kv:
Kv =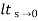 s G(s)
s G(s)
=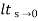 1/s(s+a) (1+b)
1/s(s+a) (1+b)
kv = 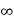
ess =1/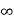 = 0
= 0
o/p tracking the o/p
(b) ka:
Ka= 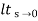 s2G(s)
s2G(s)
=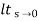 1/(s+a) (s+b)
1/(s+a) (s+b)
Ka = 1/ab
ess = 1/(yab) ≠0
o/p not locking the i/p
Key takeaway:
ess | Type 0 | Type 1 | Type 2 |
Unit step | ≠0 | 0 | 0 |
Ramp | 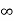 | ≠0 | 0 |
Parabolic | 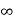 | 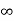 | ≠0 |
References:
1. Benjamin C. Kuo, “Automatic control systems”, Prentice Hall of India, 7th Edition.
2. M. Gopal, “Control System – Principles and Design”, Tata McGraw Hill, 4th Edition.
3. N. J. Nagrath and M. Gopal, “Control System Engineering”, New Age International Publishers, 5th Edition.
4. K. Ogata, “Modern Control Engineering”, Prentice Hall India Learning Private Limited; 5th Edition.