Unit 5
State Space Representation
The state of a system is a minimal set of variables known as state variables. The knowledge of these variables at any instance of time together with the knowledge of the inputs for the same instance of time, determines the complete behaviour of the system. The fewer drawbacks in the transfer function method for representing any system led to the use of state variables in analysis of system. Few advantages are listed below:
- The state space can be used for linear or nonlinear, time-variant or time-invariant systems.
- It is easier to apply where Laplace transform cannot be applied.
- The nth order differential equation can be expressed as 'n' equation of first order.
- It is a time domain method.
- As this is time domain method, therefore this method is suitable for digital computer computation.
- On the basis of the given performance index, this system can be designed for an optimal condition.
Representation of state space: The system shown below has ‘m’ inputs, ‘p, outputs and ‘n’ number of state variables. The state equation gives us the relation between the state variables and the inputs.
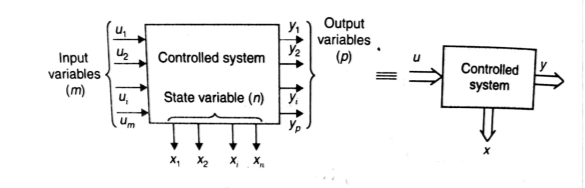
Fig 1 Representation of State space
So, the above system shown can be described through equations as
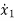 =f1 (x1, x2,…….xn , u1, u2……… ,um)
=f1 (x1, x2,…….xn , u1, u2……… ,um)
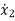 = f2 (x1, x2,…….xn , u1, u2……… ,um)
= f2 (x1, x2,…….xn , u1, u2……… ,um)
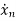 =f1 (x1, x2,…….xn , u1, u2……… ,um) (1)
=f1 (x1, x2,…….xn , u1, u2……… ,um) (1)
The above set of equations can be represented as
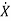 =f(x(t),u(t)) (2)
=f(x(t),u(t)) (2)
As we are concerned for time invariant system, for which the term 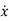 in (1) is linear combination of state variables and input. So,
in (1) is linear combination of state variables and input. So,
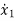 (t)=2tx1+x2+u1+u2 (3)
(t)=2tx1+x2+u1+u2 (3)
 =a11x1(t)+a12x2(t)+…a1nxn(t)+b11u1(t)+b12u2(t)+…….+b1mum(t)
=a11x1(t)+a12x2(t)+…a1nxn(t)+b11u1(t)+b12u2(t)+…….+b1mum(t)
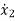 =a21x1(t)+a22x2(t)+…a2nxn(t)+b21u1(t)+b22u2(t)+…….+b2mum(t)
=a21x1(t)+a22x2(t)+…a2nxn(t)+b21u1(t)+b22u2(t)+…….+b2mum(t)
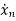 =an1x1(t)+an2x2(t)+…annxn(t)+bn1u1(t)+bn2u2(t)+…….+bnmum(t)
=an1x1(t)+an2x2(t)+…annxn(t)+bn1u1(t)+bn2u2(t)+…….+bnmum(t)
The above equation can be represented in matrix form as given below
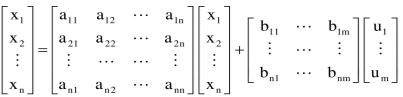 (4)
(4)
The above coefficients aij and bji in equation (4) can be written in vector matrix form as
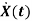 =Ax(t)+Bu(t) (5)
=Ax(t)+Bu(t) (5)
The output of the system can be represented by linear combination of state variables and inputs.
y1=c11x1(t)+c12x2(t)+…….+c1nxn+d11u1+………..+d1mum
y2=c21x1(t)+c22x2(t)+…….+c2nxn+d21u1+………..+d2mum
yr=cr1x1(t)+cr2x2(t)+…….+crnxn+dr1u1+………..+drmum (6)
The equation (6) can be represented in matrix form as  (7)
(7)
Where coefficients cij and dji are constants. The output equation is given as
Y=CX+DU (8)
Key takeaway
i) The state equation is given as  =Ax(t)+Bu(t)
=Ax(t)+Bu(t)
Ii) The output equation is given asY=CX+DU
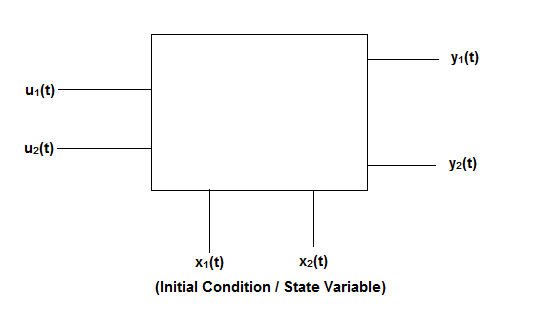
Fig2: State model
The above figure shows the state model of a system with two inputs u1(t) and u2(t), and having outputs y1(t) and y2(t). As discussed in above section 5.1, we know that the output equation is given as
Y(t)=Cx(t)+Du(t) (9)
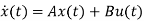 (10)
(10)
Taking L.T of equation (9)
Y(s)=CX(s)+DU(s) (11)
Taking L.T of equation (10)
SX(s)=AX(s)+BU(s) (12)
X(s)=[SI-A]-1BU(s) (13)
Y(s)=CX(s)+DU(s)
Y(s)=C{[SI-A]-1BU(s)} + DU(s)
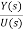 = C{[SI-A]-1B} + D (14)
= C{[SI-A]-1B} + D (14)
[SI-A]-1=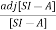
The denominator of equation (14) is the characteristic equation
[SI-A]=0
The state variables selected here are the physical quantities of the system, which can be measured. The selection of these variables can be directly related to the physical system because the solution of state equation is related to the time variation of the system variables.
The number of energy - storing elements in any system is equal to the number of state variables. Below shown are few electrical circuits, just to brush up the concept of energy storing elements and state variable relation.

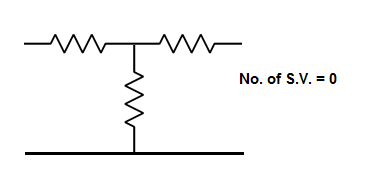
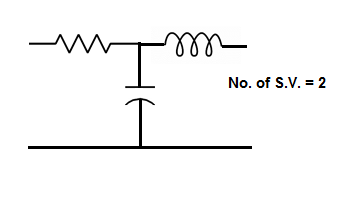
Fig 3 Electrical Circuits with energy storing elements
Now calculating the state equation and output equation for state variable analysis.
State Equation and Output equation:
Number of output = Number of output equation
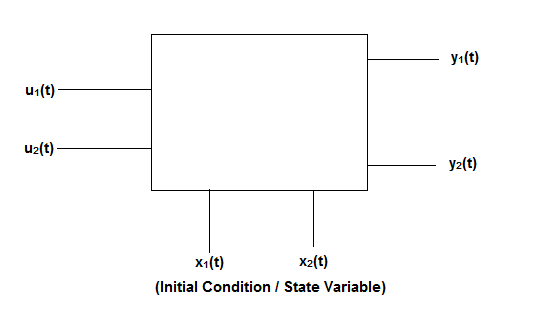
Fig 4 State Model
Considering multiple input and multiple output system, with two inputs u1(t)and u2(t), and two outputs y1(t) and y2(t) respectively.
y1(t)=c11x1(t)+c12x2(t)+d11u1(t)+d12u2(t)
y2(t)=c21x1(t)+c22x2(t)+d21u1(t)+d22u2(t)
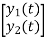 =
=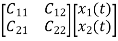 +
+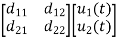
The output equation is given as
Y(t)=CX(t)+DU(t)
Y(t)=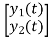 X(t)=
X(t)=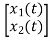
C=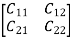 D=
D=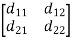
U(t)=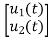
# Now finding State Equation
Number of energy storing elements= Number of state variables 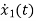 =
=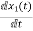 =a11x1(t)+a12x2(t)+b11u1(t)+b12u2(t)
=a11x1(t)+a12x2(t)+b11u1(t)+b12u2(t)
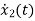 =
= =a21x1(t)+a22x2(t)+b21u1(t)+b22u2(t)
=a21x1(t)+a22x2(t)+b21u1(t)+b22u2(t)
 =
=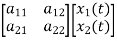 +
+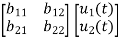
The state equation is then given as
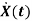 =Ax(t)+Bu(t)
=Ax(t)+Bu(t)
Key takeaway
i) The number of energy storing element= Number of state variables
Ii) We should always take voltage across the inductor L, and current through capacitor C.
Question: Obtatin the state space representation for the given electircal system
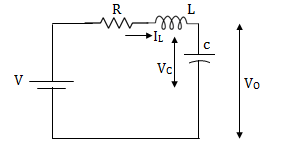
Solution: The state model is given as
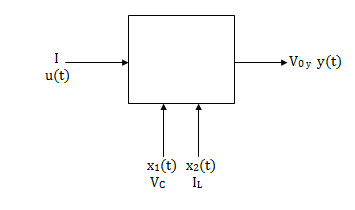
Fig 5 State Model
The state model shows that there are two energy storing elements L, C. As we already know that Number of state variables is equal to the number of energy storing elements.Hence we have two state variables[x1(t) and x2(t)]. We have one output V0(taken across capacitor) and input u(t).
The output equation is then given as
Y(t)=CX(t)+DU(t)
V0=Vc= x1(t) ….(a)
Hence output equation becomes
V0= x1(t)
y(t)=[1 0] +[0]u(t)
+[0]u(t)
So, C=[1 0] D=[0]
Now writing the state equation
 =Ax(t)+Bu(t)
=Ax(t)+Bu(t)
For that applying KVL in the above circuit
V=ILR+L +Vc
+Vc
State Equation is 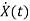 =Ax(t)+Bu(t)
=Ax(t)+Bu(t)
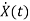 =
=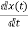
x1(t)=Vc
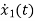 =
=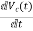
IL=C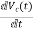
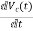 =
=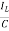
 =
=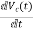 =
=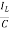
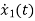 =(1/C) x2(t) ……….(b)
=(1/C) x2(t) ……….(b)
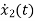 =
=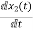 =
=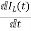
VL=L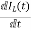
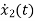 =
=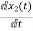 =VL/L
=VL/L
From KVL
L =VL=V-ILR-VC
=VL=V-ILR-VC
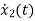 =
=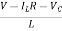 =
=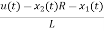
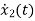 =
=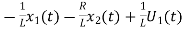 …………….(c)
…………….(c)
From equation (b) and (c)
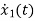 = [0 1/c]
= [0 1/c]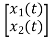 + [0 0]u(t)
+ [0 0]u(t)
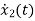 =[-1/L -R/L]
=[-1/L -R/L]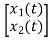 + [1/L 0]
+ [1/L 0]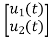
Now writing the state equation
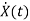 =Ax(t)+Bu(t)
=Ax(t)+Bu(t)
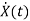 =
=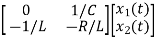 +
+ 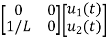
Hence A=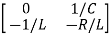 B=
B= 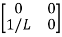
Question: Obtatin the state space representation for the given electircal system
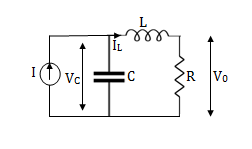
Solution: The state model shows that there are two energy storing elements L, C. As we already know that Number of state variables is equal to the number of energy storing elements.Hence we have two state variables[x1(t) and x2(t)]. We have one output V0(taken across capacitor) and input u(t).
Fig 6 State Model
Here output is V0. But from above electrical circuit V0=ILR
V0=x2(t)R
y(t)= V0= [0 R]  + [0] u(t)
+ [0] u(t)
The output equation is given as
Y(t)=CX(t)+DU(t)
C=[0 R] D=[0]
Now finding state equation,we apply KCL in the given electrical circuit
I=IC+IL
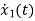 =
=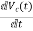
But I-IL=IC
 =
=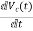
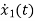 =
=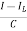
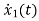 =
=
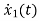 =
=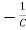 x2(t)+
x2(t)+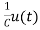 ……..(a)
……..(a)
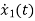 =[0 1/C]
=[0 1/C]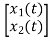 + [1/C 0]
+ [1/C 0]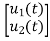 …….(b)
…….(b)
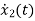 =
=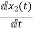 =
=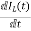
Applying KVL in the given electrical circuit we get
VC=VL+ILR
VC-ILR=VL=L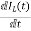
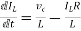
 =
=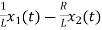
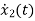 =[1/L -R/L]
=[1/L -R/L]  + [0] u(t) ………….(c)
+ [0] u(t) ………….(c)
From equation (b) and (c) we have
Now writing the state equation
 =Ax(t)+Bu(t)
=Ax(t)+Bu(t)
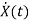 =
=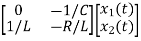 +
+ 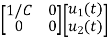
Hence A=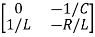 B=
B= 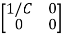
Note: We should always take voltage across the inductor L, and current through capacitor C.
The phase variables are defined as the state variables obtained from any one of the system variables and its derivatives. The nth order linear differential equation for given input y(t) and output u(t) is given as
y(n)+a1y(n-1)+………..+an-1 +any=bou(m)+……+bm-1
+any=bou(m)+……+bm-1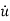 + bm u. ….. (15)
+ bm u. ….. (15)
The initial conditions are expressed as y(0),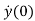 ,…..,y(n-1)(0).
,…..,y(n-1)(0).
The transfer function assuming all initial conditions zero is
T(s)=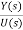 =[b0sm+b1sm-1+….+bm-1s+bm/[sn+a1sn-1+……..+an-1s+an] ……(16)
=[b0sm+b1sm-1+….+bm-1s+bm/[sn+a1sn-1+……..+an-1s+an] ……(16)
Considering simple case when there are no zeros in the system, the transfer function becomes
T(s)= =[b]/ [sn+a1sn-1+……..+an-1s+an] …….(17)
=[b]/ [sn+a1sn-1+……..+an-1s+an] …….(17)
For above transfer function the differential equation is given as
y(n)+a1y(n-1)+………..+an-1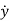 +any=b u …….(18)
+any=b u …….(18)
Let x1=y
x2=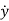
…….
xn=y(n-1)
From (18) the differential equation is given as
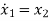

……….
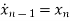
 =-anx1-an-1x2-…….-a1xn+bu
=-anx1-an-1x2-…….-a1xn+bu

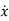 =Ax+Bu ……….(19)
=Ax+Bu ……….(19)
Note: Matrix A is known as Bush form or companion form. Matrix B has all elements zero except the last element.
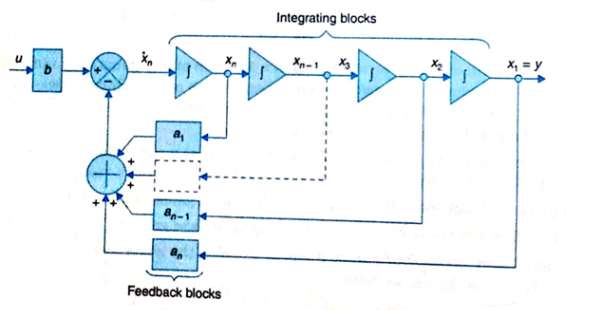
Fig 7 Phase Variable form realisation
The output equation is given as y=x1
y=Cx ……….(20)
Where C =[1 0 0………..0]
The phase variable formation for the transfer function can be obtained by the below mentioned two canonical forms.
Controllable canonical form, Observable canonical form
Observable Canonical Form:
An Observable canonical form is used to analyse and design control systems because this form allows observability. A system is observable if all its states can be determined by the output. Consider a transfer function of third order
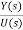 =T(s)=(b0s3+b1s2+b2s+b3)/(s3+a1s2+a2s+a3)
=T(s)=(b0s3+b1s2+b2s+b3)/(s3+a1s2+a2s+a3)
T(s)=(b0+b1/s+b2s2+b3/s3)/[1-(-a1/s-a2/s2-a3/s3)] …………(1)
By Mason’s Gain Formula
T=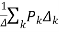 …………(2)
…………(2)
Pk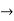 forward path transmittance of k+n path from a specified i/p node to n o/p nodes
forward path transmittance of k+n path from a specified i/p node to n o/p nodes
While calculating ipnode to n o/p nodes.
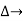 it is the graphics determined which involves of transmittances and multiple increases b/w non touching loops.
it is the graphics determined which involves of transmittances and multiple increases b/w non touching loops.
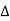 = 1- [sum of all individual loop transmitting]
= 1- [sum of all individual loop transmitting]
+[ sum of loop transmittance product of all possible non- touching loops]
-[sum of loop transmittance of all possible triples of non- touching loops]
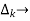 path factor associated with concered path & involves all a in the graphic which are isolated from forward path under consideration.
path factor associated with concered path & involves all a in the graphic which are isolated from forward path under consideration.
The path factor  for kthis equal to graph determinant of SFG which effect after erasing the kth path from the graph.
for kthis equal to graph determinant of SFG which effect after erasing the kth path from the graph.
The required SFG is shown below, we can conclude
y=x1+b0u
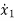 =-a1(x1+b0u)+x2+b1u
=-a1(x1+b0u)+x2+b1u
=-a1x1+x2+(b1-a1b0)u ……….(3)
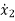 =-a2x1+x3+(b2-a2b0)u ……….(4)
=-a2x1+x3+(b2-a2b0)u ……….(4)
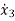 =-a3x1+(b3-a3b0)u …………(5)
=-a3x1+(b3-a3b0)u …………(5)
y=[1 0 0] +b0u ………….(6)
+b0u ………….(6)
The resulting matrix is given below
The above equations in matrix form can be easily interpreted through the signal flow graph. From the equation (3) and (5) we can say that
a) There are three feedback loops touching each other and having gain -a1/s, -a2/s2 and -a3/s3.
b) There are four forward paths touching the loop and having gain b0, b1/s, b2/s2, b3/s3.
So, the signal flow graph is shown below
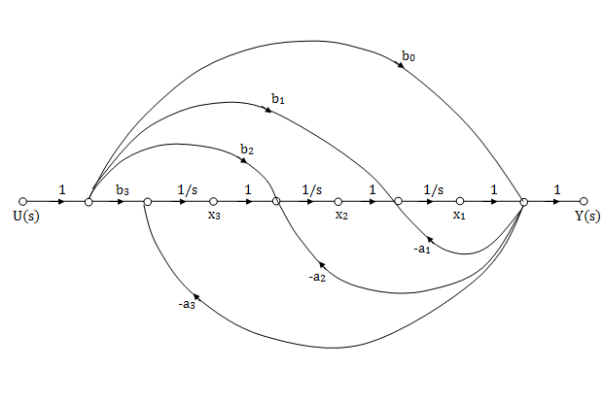
Fig 8: SFG for observable Form
Question: Find the observable canonical realization of the system H(s)=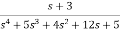
Solution: The above transfer function can be also written as
H(s)=
Comparing above equation with standard equation we conclude that
The gains of forward paths are 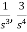
The feedback loop gains are 
The SFG satisfying above conditions will be
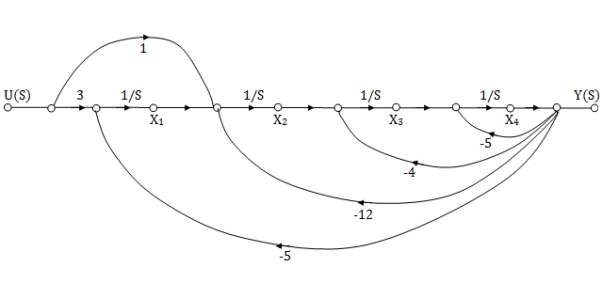
The observable canonical form can be obtained by converting the above SFG to block diagram
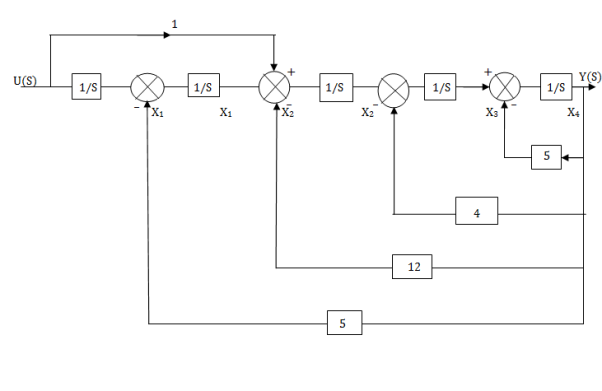
Fig 9 observable canonical form can be obtained by converting the above SFG to block diagram
Controllable Canonical Form: In this the transfer function is divided into two parts as shown in below figure.
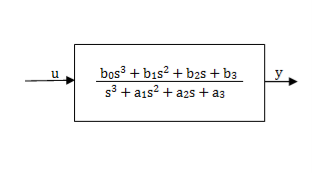
Fig 10: A third order system

Fig 11: Simplified representation of above system
G(s)=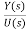 =
= 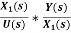
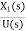 =
= ………..(7)
………..(7)
 =b0s3+b1s2+b2s+b3
=b0s3+b1s2+b2s+b3
The equation relating phase variable to input is given as

The equation relating output to phase variable can be given as(refer eq.(7))
y=b0 +b1
+b1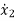 +b1
+b1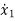 +b3x1
+b3x1
=b0(-a3x1-a2x2-a1x3+u)+b1x3+b2x2+b3x1
=(b3-a3b0)x1+(b2-a2b0)x2+(b1-a1b0)x3+b0u
The above equation in vector matrix form can be written as
y=[((b3-a3b0) (b2-a2b0) (b1-a1b0)]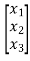 +b0u ……..(8)
+b0u ……..(8)
The signal flow graph for above vector matrix equations is shown below
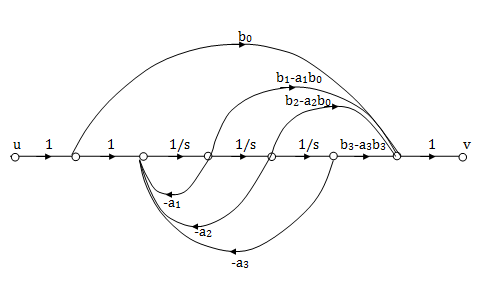
Fig 12: SFG for controllable form
Key takeaway
i) Matrix A is known as Bush form or companion form. Matrix B has all elements zero except the last element.
Ii) A system is observable if all its states can be determined by the output
Question: Find the controllable canonical realization of the following systems
a) H(s)=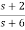
b) H(s)=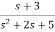
Solution: a) H(s)=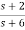
Let H(s)=
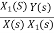 =
=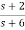
H1(s)= 1/s+6
1/s+6
X(s)=sX1(s)+6X1(s)
SX1(s)= X(s) +6X1(s)
We can get X1(s) by passing sX1(s) through integrator. The above equation can be realised as
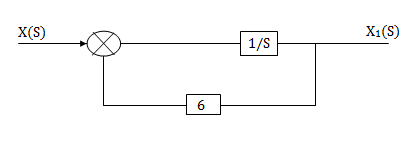
Fig 13 H1(s)= 1/s+6
1/s+6
H2(s)= s+2
s+2
Similarly, Y(s)= sX1(s)+2X1(s)
H2(s)= s+2
s+2

Fig 14 H2(s)=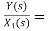 s+2
s+2
The complete realization of transfer function can be obtained by combining the above two realizations. The complete realization will be
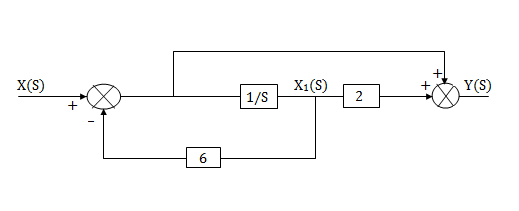
Fig 16 complete realization of H(s)=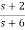
b)H(s)=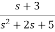
Let H(s)=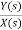 =
= 
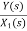 =s+3
=s+3
Y(s)=sX1(s)+3X1(s)
The above transfer function can be realised as
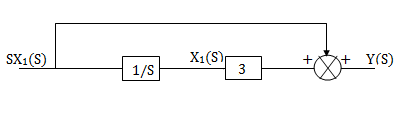
Fig 17 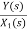 =s+3
=s+3
Now, 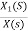 =
=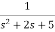
s2X1(s)=X(s)-2sX1(s)-5X1(s)
Assuming s2X1(s) is available the above transfer function can be realised as
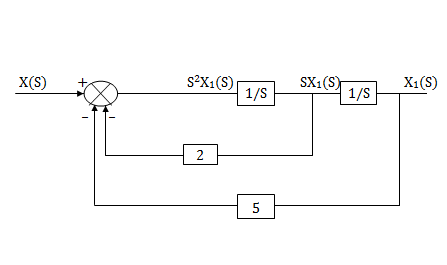
Fig 18 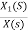 =
=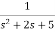
The complete realization of transfer function can be obtained by combining the above two realizations. The complete realization will be
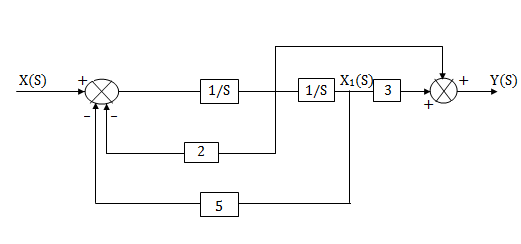
Fig 19 H(s)=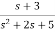
The first order differential equation is given as
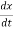 =ax x(0)=x0
=ax x(0)=x0
x(t)=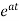 x0=
x0=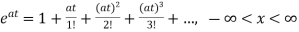
Consider state equation
 =Ax(t); x(0)=x0
=Ax(t); x(0)=x0
The solution will be of the form
x(t)=a0+a1t+a2t2+a3t3+….+aiti
Substituting value in above equation
a1+2a2t2+3a3t3+……….=A[a0+a1t+a2t2+a3t3+….+aiti]
a1=Aa0
a2= Aa1=
Aa1=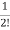 A2a0
A2a0
ai= Aia0
Aia0
Solution for x(t) will be
x(t)=[I+At+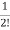 A2t2+………+
A2t2+………+ Aiti]x0
Aiti]x0
The matrix exponential form can be written as

The solution x(t) will be x(t)=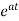 x0
x0
 =Ax(t)+Bu(t) and x(0)=x0
=Ax(t)+Bu(t) and x(0)=x0
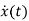 - Ax(t)=Bu(t)
- Ax(t)=Bu(t)
Multiplying both sides by 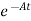
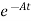 [
[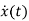 - Ax(t)]=
- Ax(t)]= =
=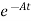 Bu(t)
Bu(t)
Integrating both sides w.r.t t we get
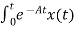 =
= 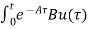 d
d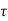
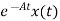 =
=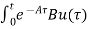 d
d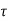
Multiplying both sides by 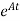
x(t)=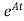 x(0)+
x(0)+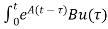 d
d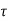
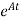 x(0) is called as Homogeneous solution
x(0) is called as Homogeneous solution
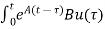 d
d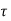 is the Forced solution
is the Forced solution
At t=t0
x(t)=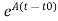 x(t0)+
x(t0)+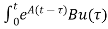 d
d
The above equation is the required solution.
State Transition Matrix and its Properties:
y(t)=Cx(t)+Du(t)
x(t)=Ax(t)+Bu(t)
 -Ax(t)=Bu(t)
-Ax(t)=Bu(t)
SX(s)-X(0)-AX(s)=BU(s)
SX(s)-AX(s)=BU(s)+X(0)
[SI-A]X(s)=X(0)+BU(s)
X(s)=[SI-A]-1[X(0)+BU(s)]
X(s)=[SI-A]-1X(0)+[SI-A]-1BU(s) (a)
This is solution of state differential equation
L-1X(s)= L-1{[SI-A]-1X(0)+[SI-A]-1BU(s)}
x(t)= [SI-A]-1x(0)+ [SI-A]-1Bu(t) (b)
From above x(t) we can find output equation by replacing x(t) in output equation by its value from above equation(b)
For the given system below
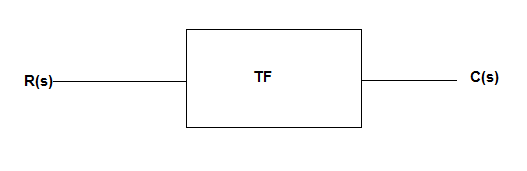
Fig 20 System with Transfer function TF
TF=c(t)/r(t)
This c(t) is output of present system, which is not equal to above y(t), as their initial conditions are not considered.
If initial conditions are zero than both y(t) and c(t) will be equal to
L-1[SI-A]-1=φ(t)…….. State transition matrix
Φ(s)=[SI-A]-1
x(t)=φ(t)x(0)+L-1[φ(s)* BU(s)] (c)
State transition matrix satisfies the solution of state equation when input is zero. [u(t)=0]
 =Ax(t)+Bu(t)
=Ax(t)+Bu(t)
As u(t)=0
 =Ax(t)
=Ax(t)
 -Ax(t)=0
-Ax(t)=0
Solution to above equation is
y(t)=Ke-Pt+e-Pt∫ ePt Q d(t)
But 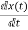 -Ax(t)=0
-Ax(t)=0
Hence above equation becomes
X(t)=AeAt
Substitute t=0
x(0)=ke0
x(0)=k
x(t)=x(0)eAt (zero input response)
Properties of state transition matrix:
From equation (31) when u(t)=0
x(t)=φ(t) x(0)
And from zero input response we have
φ(t)=eAt
Property 1:
φ(0)= [I]
Property 2:
Φ-1(t)= [φ(t)]-1=e-At=eA(-t)
Φ-1(t)= Φ(-t)
Property 3:
ΦK(t)= [Φ(t)]K
ΦK(t)=[eAt]K=eA(tK)
ΦK(t)= Φ(Kt)
Property 4:
Φ(t1+t2)=eA(t1+t2)
=e(At1+At2)=eAt1 * eAt2
Φ(t1+t2)= Φ(t1)Φ(t2)
Property 5:
Φ(t2-t1) * φ(t1-t0)=eA(t2-t1) * eA(t1-t0)
=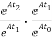
=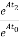 =eA(t2-t0)
=eA(t2-t0)
Φ(t2-t1) * φ(t1-t0)= Φ(t2-t0)
Key takeaway
i) x(t)= x (0) eAt (zero input response)
Ii) L-1[SI-A]-1=φ(t) state transition matrix
Iii) Φ (0) = [I]
Iv) Φ-1(t)= Φ(-t)
v) ΦK(t)= Φ(Kt)
Vi) Φ(t1+t2) = Φ(t1) Φ(t2)
Vii) Φ(t2-t1) * φ(t1-t0) = Φ(t2-t0)
Question: A=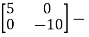 . Find the state transition matrix?
. Find the state transition matrix?
Solution: The state transition matrix is given by L-1[SI-A]-1=φ(t)
[SI-A]=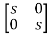
 -
-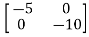
=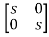 -
-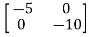
=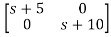
Taking inverse Laplace of above, we get
[SI-A]-1=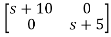 /(S+5)(S+10)
/(S+5)(S+10)
=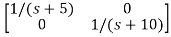
Hence φ(t)=L-1[SI-A]-1=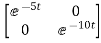
Question: Find state transition matrix if A=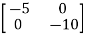
Solution: The state transition matrix is given by L-1[SI-A]-1=φ(t)
[SI-A]=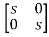 -
-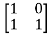
=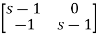
[SI-A]-1=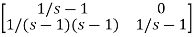
Hence φ(t)=L-1[SI-A]-1=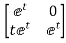
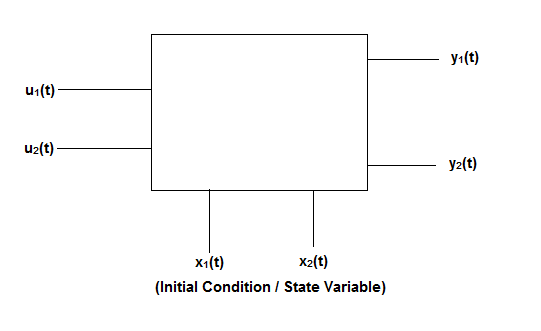
Fig 21: State model
The above figure shows the state model of a system with two inputs u1(t) and u2(t), and having outputs y1(t) and y2(t). As discussed in above section 5.1, we know that the output equation is given as
Y(t)=Cx(t)+Du(t) (9)
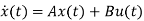 (10)
(10)
Taking L.T of equation (9)
Y(s)=CX(s)+DU(s) (11)
Taking L.T of equation (10)
SX(s)=AX(s)+BU(s) (12)
X(s)=[SI-A]-1BU(s) (13)
Y(s)=CX(s)+DU(s)
Y(s)=C{[SI-A]-1BU(s)} + DU(s)
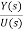 = C{[SI-A]-1B} + D (14)
= C{[SI-A]-1B} + D (14)
[SI-A]-1=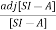
The denominator of equation (14) is the characteristic equation
[SI-A]=0
Key takeaway
The characteristic equation [SI-A]=0
Q.1) A= . Calculate characteristic equation and stability?
. Calculate characteristic equation and stability?
Sol: The characteristic equation is given as [SI-A]=0
S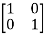 -
- 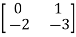 =0
=0
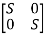 -
- = 0
= 0
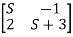 =0
=0
S(S+3)-(-1)*2=0
Hence, the characteristic equation is
S2+3S+2=0
(S+1)(S+2)=0
S=-1,-2
Both roots on left-half of s-plane, real and different, system absolutely stable.
Q.2)A= 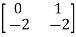 Find the characteristic equation and comment on stability?
Find the characteristic equation and comment on stability?
Sol: The characteristic equation is given by [SI-A]=0
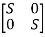 -
-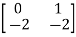 =0
=0
 =0
=0
S(S+2)+2=0
S2+2S+2=0
S=-1±j
Roots on left-half of s-plane, complex conjugate, system absolutely stable.
References:
1. Benjamin C. Kuo, “Automatic control systems”, Prentice Hall of India, 7th Edition.
2. M. Gopal, “Control System – Principles and Design”, Tata McGraw Hill, 4th Edition.
3. N. J. Nagrath and M. Gopal, “Control System Engineering”, New Age International Publishers, 5th Edition.
4. K. Ogata, “Modern Control Engineering”, Prentice Hall India Learning Private Limited; 5th Edition.