Unit - 5
Uniform Plane Waves
The static electric field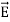 
exist without a magnetic field 
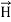demonstrated by a capacitor with static charge Q.
Similarly, a conductor with constant current I has magnetic field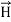 
in absence of an electric field
.
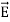But in time varying fields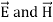 
cannot exist without each other.
Maxwell’s equations are nothing but set of four expressions derived from Ampere’s circuit law, Farady’s law, Gauss’s law for electric field and Gauss’s law for magnetic field.
- Maxwell’s equation derived from Faradays law:
According to the concept from electrostatic field the work done over a closed path or closed contour that is starting point same as terminating point is always zero.
Mathematically it can be represented as
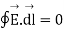-----------------------(1)
The above equation is called integral form of Maxwell’s equation derived from Faradays law of static field.
Using Stroke’s theorem converting close line integral into surface integral we get
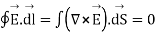
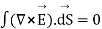
But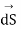 
cannot be zero which means 
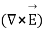= 0.
Point form of Maxwell’s equation derived from differential form.
- Maxwell’s equation derived from Ampere’s Circuital Law:
According to the basic concept of magnetostatics an Amper’s circuital law states that the line integral of magnetic field intensity 
around closed path is exactly equal to direct current enclosed by that path.
Mathematically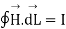 
Now the current enclosed is equal to the product of current density normal to the closed path and area of closed path. Hence, we get
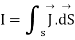where
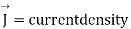
Hence evaluating the above equations, we get
The above expression is integral form of Maxwell’s equation from Ampere circuital law for static field.
Now by applying Stoke’s theorem LHS of the equation can be converted into surface integral
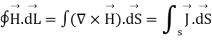
Hence, we get
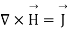
- Maxwell’s equation derived from Gauss Law:
According to Gauss law of electrostatic fields the electric flux through any closed surface is equal to the total charge enclosed by that surface. Mathematically we can write
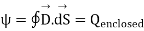1
The most common form to represent Gauss law mathematically is volume charge density Pv hence, we can write
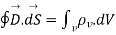----2
The above equation is called integral form of Maxwell’s equation derived from Gauss Law.
To establish the relationship between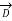 
and Pv converting closed surface integral into volume integral using divergence theorem as
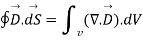----3
Comparing 2 and 3 we get
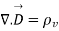
- Maxwell’s equation derived from Gauss Law for Magnetostatic field.
According to Gauss law for magneto static field the magnetic flux cannot reside in closed surface due to non-existence of single magnetic pole.
Mathematically we can write
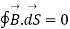
The above equation is called Integral form of Maxwell’s equation derived from Gauss law for static magnetic field.
Now using divergence theorem, we can write
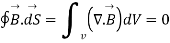
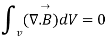
Now dV cannot be zero that means 
.
From Faradays Law we have specifications µ,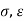
0.
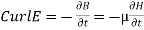---------(1)
Applying µ,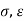
0
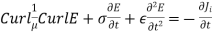------------------(2)
Because µ is constant we can take it out of the curl and multiply the whole equation
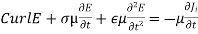----------------------(3)
We can rewrite the curl in the following form
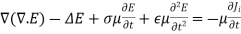--------------------------------(4)
Furthermore, we also know that
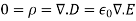
This relation brings us nearly to the Helmholtz equation in vector form
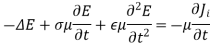
Maxwell’s equation in free space is given by
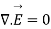------------------------(1)
This gives a relation between the amplitude vector E~ 0 and the wave vector ~k as
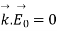-------------------------(2)
Since E~ 0 gives the direction of the electric field at all points in space, and ~k gives the direction of propagation of the wave, equation (2) tells us that plane electric waves in free space are transverse waves.
We can also derive a wave equation for the magnetic field, starting from Maxwell’s equation (in free space):
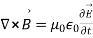---------------------------(3)
Taking the curl, as before, and using a vector identity gives:
-------------------------(4)
Using ∇· B~ = 0, and substituting for ∇× E~ from Maxwell’s equation gives:
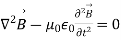--------------------------------(5)
Which has the solution:
------------------------------------------(6)
To check that our solution for the magnetic wave equation satisfies Maxwell’s equations.
In this case, we find from ∇· B~ = 0 that the wave is once again a transverse wave
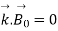-----------------------------------------(7)
The solutions for the electric and magnetic fields simultaneously satisfy Maxwell’s equations. We find
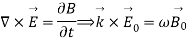
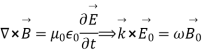
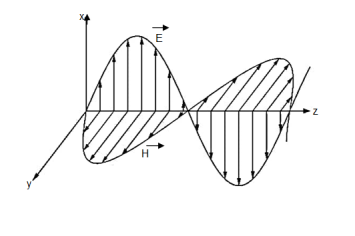
These results tell us that the electric and magnetic fields and the wave vector must be mutually perpendicular.
We also find the relationship between the amplitudes of the electric and magnetic fields
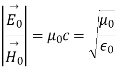
Where c is
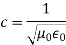
The ratio between the amplitudes of E~ and H~ in a plane wave in free space defines the impedance of free space, Z0:
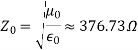
The penetration of a wave in a material is about its wavelength.
- The penetration is expressed in cm or dm.
- The penetration of waves of low frequency (HF, MF and BF) is expressed in m.
- The penetration of light waves and infrared is expressed in microns.
Penetration of different mediums
From Maxwell’s equation in electric field E and magnetic field H the following equations of the propagation of the wave is:
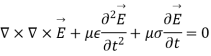
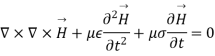
Let us pass in the field of Fourier then
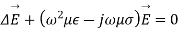
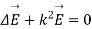
The last equation is known as Helmholtz where:
Ist case:
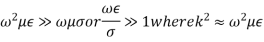
Here k is real. Hence, EM waves are sensitive to the dielectric permittivity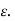 
For temporal field we have
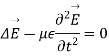
It is the term of propagation.
2nd case: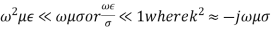 
The physical property is the electrical conductivity σ . In the temperal field
The amplitude decreases with distance characteristics.
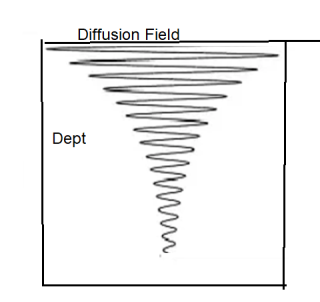
An EM wave will see its amplitude decreasing by a factor 1/e to a depth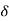 
= 1/β m.
The electromagnetic wave consists of electric and magnetic fields vibrating at right angles to each other therefore it is necessary to adopt a convention to determine the polarisation of the signal. For this purpose, an electric field is used.
Vertical and horizontal polarisation fall into the category known as linear polarisation. The wave can be thought of as vibrating in one plane which is up and down or side to side.
Circular polarisation can be visualised by imagining a signal propagating from an antenna that is rotating. The tip of the electric field vector can be seen to trace out a helix or corkscrew as it travels away from the antenna.
Circular polarisation can be either right or left- handed dependent upon the direction of rotation as seen from the transmitting antenna.
Elliptical polarisation. This occurs when there is a combination of both linear and circular polarisation. This can be visualised by imagining the tip of the electric field tracing out an elliptically shaped corkscrew.
Problem:
Determine the polarization of a plane wave with
a)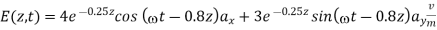 
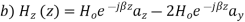
Solution
(a) From the given E,
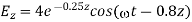
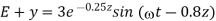
In the z=0 plane, we have
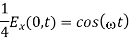
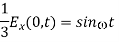
Squaring and adding gives
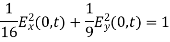
Which describes an ellipse. Hence the wave is elliptically polarized.
(b) The two components of H are in phase; hence, the polarization is linear. For proper characterization, it is expedient to find the electric field component. This can be done in many ways. Using Maxwell’s equation,
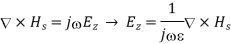
Dividing both sides by j and setting =bl yields
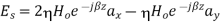
In the time domain,
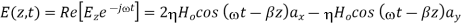
If we set z=0
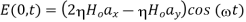
At t=0, E has components 2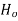
In the x-direction and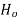 
in the -direction. The ration 
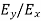remains the same as t changes. Hence E is linearly polarized.
A uniform plane wave with x-directed electric field is normally incident upon a perfectly conducting plane at z =0, as shown in Figure. The presence of the boundary gives rise to a reflected wave that propagates in the -z direction. There are no fields within the perfect conductor. The known incident fields traveling in the +z direction can be written as
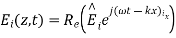
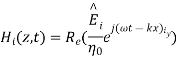
While the reflected fields propagating in the -z direction are similarly
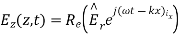
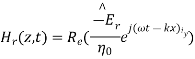
Where in the lossless free space
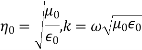
The minus sign difference in the spatial exponential phase factors of (1) and (2) as the waves are traveling in opposite directions. The amplitude of incident and reflected magnetic fields are given by the ratio of electric field amplitude to the wave impedance.
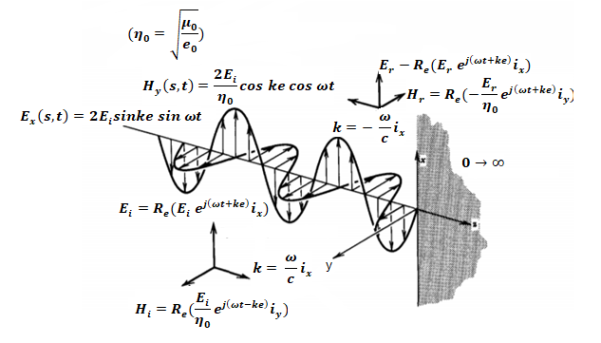
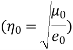
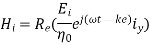
The negative sign in front of the reflected magnetic field for the wave in the -z direction arises because the power flow S, = E, x H, in the reflected wave must also be in the -z direction. The total electric and magnetic fields are just the sum of the incident and reflected fields. The only unknown parameter E, can be evaluated from the boundary condition at z =0 where the tangential component of E must be continuous and thus zero along the perfect conductor:
The total fields are the sum of incident and reflected fields
=
=
=
=
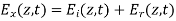
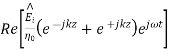
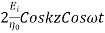The electric and magnetic fields are 90* out of phase with each other both in time and space.
The perfect conductor with a lossless dielectric of permittivity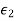 
and permeability 
, as in Figure with a uniform plane wave normally incident from a medium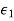 
with permittivity and permeability 
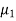. In addition to the incident and reflected fields for z 0.
The unknown quantities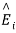 
and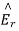 
can be found from the boundary conditions of continuity tangential E and H at z=0,
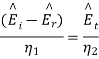
From which we find reflection R and transmission field T field coefficients as
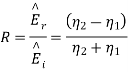
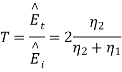
Where 1 + R = T
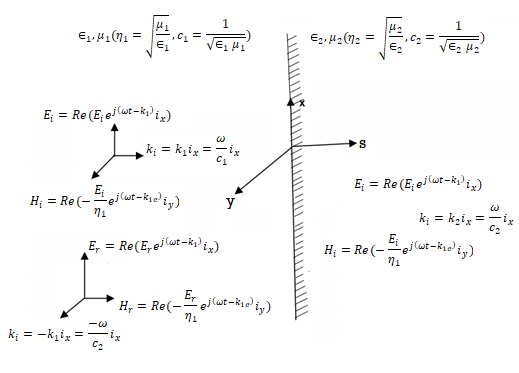
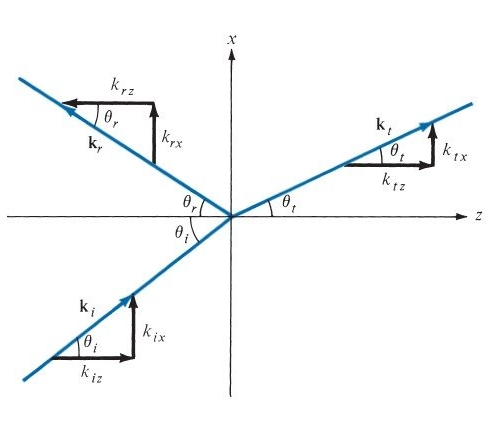
Consider reflection and refraction of uniform linearly polarized homogenous plane at horizontal interface. The incident wave is confined to xy-plane. The interface is denoted by S which has normal vector n and separates two homogeneous media with physical properties σ1, µ1,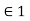
and σ2, µ2, 
.
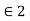The incident wave ki arrives at angle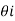 
. Once it reaches the interface it breaks into reflected wave (kr) and transmitted wave (kt). The transmitted wave experiences change in propagation direction thus it is a refracted wave.
The reflected and refracted travel in directions characterized by angles θr and θt.
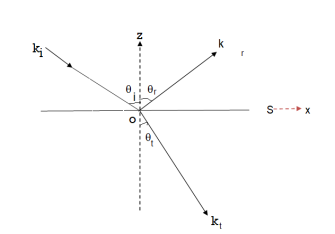
The reflection and refraction angles θr and θt can be derived by considering either the electric field or the magnetic field carried by the incident EM wave.
Here, we will derive these angles by considering an electric field. The respective incident, reflected and refracted waves are given by:
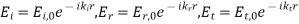
Where kis the wave vector (Poynting vector) for each wave and:
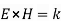
They state that components of the electric field parallel to surface SS must be equal across the interface. As a result:
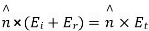
Also,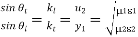 
And 
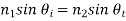
Where
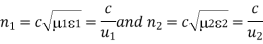
Are the refractive indices of the media.
Problem:
A uniform plane wave in air with 
Is incident on a dielectric slab (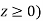
with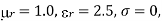 
find
(a) The polarization the wave
(b) The angle of incidence
(c) The reflected E field
(d) The transmitted H field
Solution:
(a) From the incident E field, it is evident that the propagation vector is
Hence
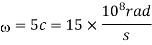
A unit vector normal to the interface (z=0) is a. The plane containing k and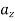 
is y=costant, which is the xz-plane, theplane of incidence. Since 
is normal to this plane. We have perpendicular (similar to figure 10.18)
(b) The propagation vectors are illustrated in figure 10.19 where it is clear that
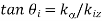=4/3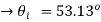 
Alternatively, without fig 10.19, we can obtain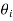 
from the fact htat 
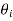is the angle between k and 
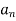that is,
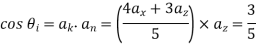
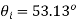
(c) An easy way to find 
is use because we have that this problem is similar to that considered in section. Suppose we are not aware of this. Let
Which is similar to form to the given 
The unit vector 
is chosen in view of the fact that the tangential component of E must be continuous at the interface. From figure,
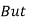
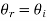and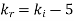 
because both 
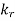and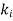 
are in the same medium. Hence,
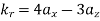
To find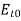 
, we need 
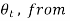Snell’s law
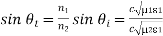
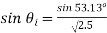
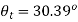
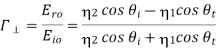
Where 
Hence,
(d) Similarly let the transmitted electric field be
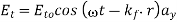
Where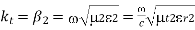 
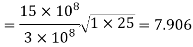
From figure,
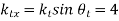
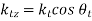=6.819
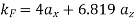
Notice that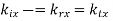 
expected
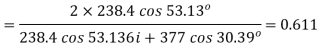
The same result could be obtained from the relation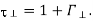 
Hence
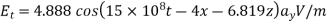
From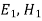 
is easily obtained as
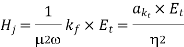
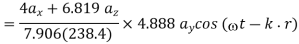
Circuit Theory
Circuit theory deals with electrical circuit. The main variables are voltage and current which are scalar quantities. This theory uses basic laws like Ohm’s law, Kirchhoff’s laws. The limitation of this theory is that it cannot be applied in free space and it is applicable at low frequencies. Also, this theory is unsuccessful in explaining the radiation of electromagnetic waves into space in radio communications.
It cannot be used to analyse or design a complete communication system. Example: Radio Communication System.
Field Theory
It involves the usage of vector quantities E and H. The main equations involved here are Maxwell’s equation, Helmholtz equation, Poisson’s equation. This theory has following advantages in comparison to circuit theory:
It is also applicable in free space.
It is useful at all frequencies, particularly at high frequencies
The radiation effect can be considered.
This theory can be used to analyze or design a complete communication system. Example: Wireless Communication, Radio Communication.
Antenna
The IEEE Standard Definitions of Terms for Antennas (IEEE Std 145–1983) defines the antenna or aerial as ―a means for radiating or receiving radio waves. In other words, the antenna is the transitional structure between free-space and a guiding device. The guiding device or transmission line may take the form of a coaxial line or a hollow pipe (waveguide), and it is used to transport electromagnetic energy from the transmitting source to the antenna or from the antenna to the receiver.
Radiation Mechanism
The radiation from the antenna takes place when the Electromagnetic field generated by the source is transmitted to the antenna system through the Transmission line and separated from the Antenna into free space.
Radiation from a Single Wire
From the principle of radiation, there must be some time varying current. For a single wire antenna,
1. If a charge is not moving, there is no current and there is no radiation.
2. If charge is moving with a uniform velocity:
There is no radiation if the wire is straight and infinite in extent.
There is radiation if the wire is curved, bent, discontinuous, terminated, or truncated, as shown in Figure.
3. If charge is oscillating in a time-motion, it radiates even if the wire is straight
Figure: Wire Configurations for Radiation
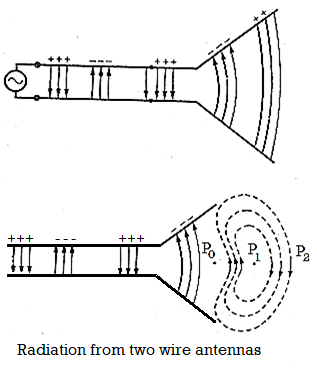
Radiation from a Two Wire
Let us consider a voltage source connected to a two-conductor transmission line which is connected to an antenna. This is shown in Figure (a). Applying a voltage across the two-conductor transmission line creates an electric field between the conductors. The electric field has associated with it electric lines of force which are tangent to the electric field at each point and their strength is proportional to the electric field intensity. The electric lines of force have a tendency to act on the free electrons (easily detachable from the atoms) associated with each conductor and force them to be displaced. The movement of the charges creates a current that in turn creates magnetic field intensity. Associated with the magnetic field intensity are magnetic lines of force which are tangent to the magnetic field. We have accepted that electric field lines start on positive charges and end on negative charges. They also can start on a positive charge and end at infinity, start at infinity and end on a negative charge, or form closed loops neither starting or ending on any charge. Magnetic field lines always form closed loops encircling current-carrying conductors because physically there are no magnetic charges. In some mathematical formulations, it is often convenient to introduce equivalent magnetic charges and magnetic currents to draw a parallel between solutions involving electric and magnetic sources.
The electric field lines drawn between the two conductors help to exhibit the Distribution of charge. If we assume that the voltage source is sinusoidal, we expect the electric field between the conductors to also be sinusoidal with a period equal to that of the applied source. The relative magnitude of the electric field intensity is indicated by the density (bunching) of the lines of force with the arrows showing the relative direction (positive or negative). The creation of time varying electric and magnetic fields between the conductors forms electromagnetic waves which travel along the transmission line, as shown in Figure (a). The electromagnetic waves enter the antenna and have associated with them electric charges and corresponding currents. If we remove part of b the antenna structure, as shown in Figure (b), free-space waves can be formed by ―connecting‖ the open ends of the electric lines (shown dashed). The free-space waves are also periodic but a constant phase point P0 moves outwardly with the speed of light and travels a distance of λ/2 (to P1) in the time of one-half of a period. It has been shown that close to the antenna the constant phase point P0 moves faster than the speed of light but approaches the speed of light at points far away from the antenna (analogous to phase velocity inside a rectangular waveguide).
Propagation of EM Energy:
Electromagnetic waves are waves, which can travel through the vacuum of outer space. Mechanical waves, unlike electromagnetic waves, require the presence of a material medium in order to transport their energy from one location to another. Sound waves are examples of mechanical waves while light waves are examples of electromagnetic waves.
Electromagnetic waves are created by the vibration of an electric charge. This vibration creates a wave, which has both an electric and a magnetic component. An electromagnetic wave transports its energy through a vacuum at a speed of 3.00 x 108 m/s (a speed value commonly represented by the symbol c). The propagation of an electromagnetic wave through a material medium occurs at a net speed, which is less than 3.00 x 108 m/s.
The mechanism of energy transport through a medium involves the absorption and reemission of the wave energy by the atoms of the material. When an electromagnetic wave impinges upon the atoms of a material, the energy of that wave is absorbed. The absorption of energy causes the electrons within the atoms to undergo vibrations. After a short period of vibrational motion, the vibrating electrons create a new electromagnetic wave with the same frequency as the first electromagnetic wave. While these vibrations occur for only a very short time, they delay the motion of the wave through the medium. Once the energy of the electromagnetic wave is reemitted by an atom, it travels through a small region of space between atoms. Once it reaches the next atom, the electromagnetic wave is absorbed, transformed into electron vibrations and then reemitted as an electromagnetic wave. While the electromagnetic wave will travel at a speed of c (3 x 108 m/s) through the vacuum of interatomic space, the absorption and reemission process cause the net speed of the electromagnetic wave to be less than c.
The actual speed of an electromagnetic wave through a material medium is dependent upon the optical density of that medium. Different materials cause a different amount of delay due to the absorption and reemission process. Furthermore, different materials have their atoms more closely packed and thus the amount of distance between atoms is less. These two factors are dependent upon the nature of the material through which the electromagnetic wave is traveling. As a result, the speed of an electromagnetic wave is dependent upon the material through which it is traveling.
Summary:
Maxwell’s Equations:
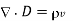
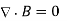
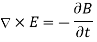
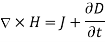
Helmholtz’s Equation: In vector form
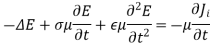
Relationship between E and H: Both vectors are mutually perpendicular.
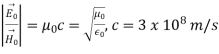
Polarization may be regarded as the locus of the tip of the electric field (in a plane perpendicular to the direction of propagation) at a given point as a function of time.
Reflection by perfect conductor-normal incidence
, 
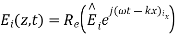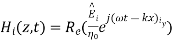are incident waves
, 
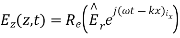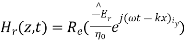are reflected waves
The total fields are the sum of incident and reflected fields
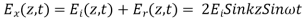
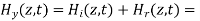
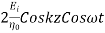
Reflection by perfect dielectric- normal incidence
R: Reflection Coefficient,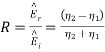 
T: Transmission Coefficient,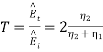 
Where 1 + R = T
Snell’s Law:
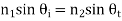
Where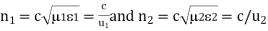 
Are the refractive indices of the media.
Circuit Theory involves voltages and currents, which are scalar quantities. Ohm’s Law and Kirchhoff’s laws are applied here. It is applicable at low frequencies and it cannot explain radiations.
Field Theory involves E and H vectors. Maxwell’s equations, Helmholtz equation are a part of this theory. It is applicable at High frequencies and can be applied in free space.
Antenna is defined as a means for radiating or receiving radio waves. The radiation from the antenna takes place when the Electromagnetic field generated by the source is transmitted to the antenna system through the Transmission line and separated from the Antenna into free space. Radiations can take place from a single wire or a two-wire antenna.
Electromagnetic waves are created by the vibration of an electric charge. Unlike mechanical waves, EM waves do not require the presence of a material medium in order to transport their energy from one location to another.
The mechanism of energy transport in EM waves through a medium involves the absorption and reemission of the wave energy by the atoms of the material. Also, the speed of EM wave is dependent on the the material through which it is traveling.
References:
1. Kraus and Flemish, “Electromagnetics with Applications”, McGraw Hill International Editions, 5th Edition.
2. Jordan and Balmain, “Electromagnetic Waves and Radiating Systems”, PHI, 1964.
3. Faraday, Maxwell, and the Electromagnetic Field: by Basil Mahon and Nancy Forbes.
4. Electromagnetism: Theory and Applications Book by Ashutosh Pramanik
5. Field and wave electromagnetics Textbook by David K. Cheng
