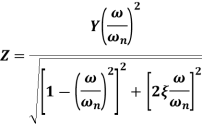Unit 2
Single Degree of Freedom Systems – Forced Vibrations
Forced Vibration
If the system vibrates under the influence of external periodic force, the vibrations are known as forced vibration.
Longitudinal Forced Vibration
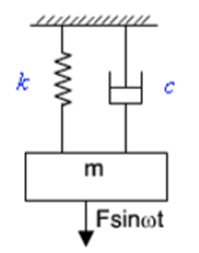
Consider a spring-mass-damper system as shown in figure.
The equation of motion of this system subjected to a harmonic force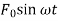
can be given by
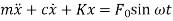
where, m , k and c are the mass, spring stiffness and damping coefficient of the system, F is the amplitude of the force, w is the excitation frequency or driving frequency.
Torsional Forced Vibration
Consider a disc having mass moment of inertia ‘I’ suspended on a shaft with negligible mass subjected to a harmonic torque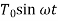 
The equation of motion for this system is given by
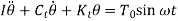
Where,
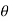= angular displacement of disc from mean position in rad
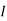= mass moment of inertia of disc = 
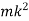kg m2
= torsional stiffness of shaft in Nm/rad
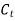= torsional damping coefficient
Consider a spring-mass-damper system as shown in figure.
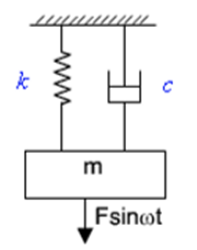
The equation of motion of this system subjected to a harmonic force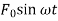
can be given by
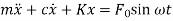
where, m, k and c are the mass, spring stiffness and damping coefficient of the system, F is the amplitude of the force, w is the excitation frequency or driving frequency.
Solution for differential equation
The complete solution of linear second order differential equation consists of two parts
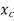
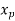
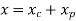
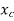
It is obtained by considering no force condition,
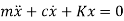
The equation is same as that of damped free vibration. So the solution is
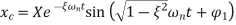
2. Particular Integral 
:
Particular Integral is in the form of
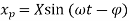
Differentiating above equation w. r. t time ‘t’, we get velocity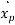 
,
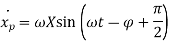
Again differentiating above equation w. r. t time ‘t’, we get acceleration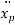 
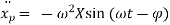
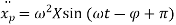
Substituting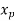 
, 
, 
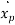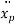in differential equation we get,
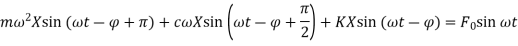
After solving trigonometrically, we get
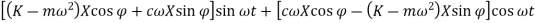
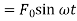
Comparing coefficients of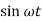 
and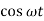 
we get
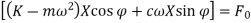
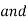
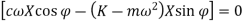
From the above equation, we get,
Phase angle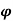 
as
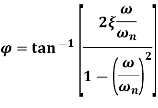
Amplitude X is
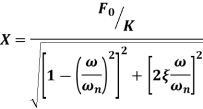
Particular integral becomes
General solution becomes,
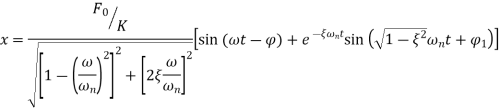
One may find many rotating systems in industrial applications. The unbalanced force in such a system can be represented by a mass m with eccentricity e, which is rotating with angular velocity as shown in Figure
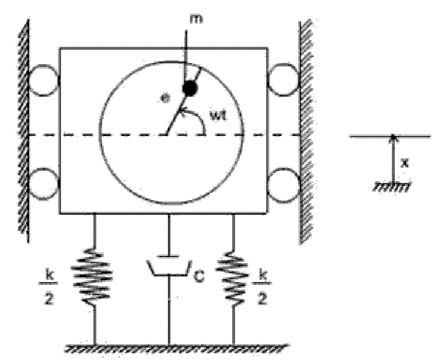
Rotating Unbalance
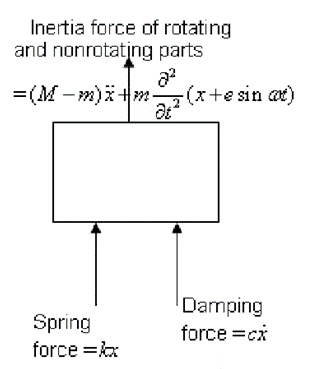
FBD of system
Let x be the displacement of the nonrotating mass (M) from the static equilibrium position, then the displacement of the rotating mass m is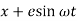 
From the free-body diagram of the system shown in figure, the equation of motion is
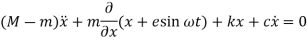
Or
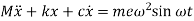
Comparing this equation with equation of forced harmonic vibration
we get
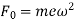
Therefore,
Since,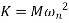 
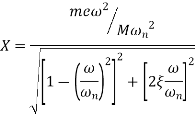
And Phase angle is
Frequency Response
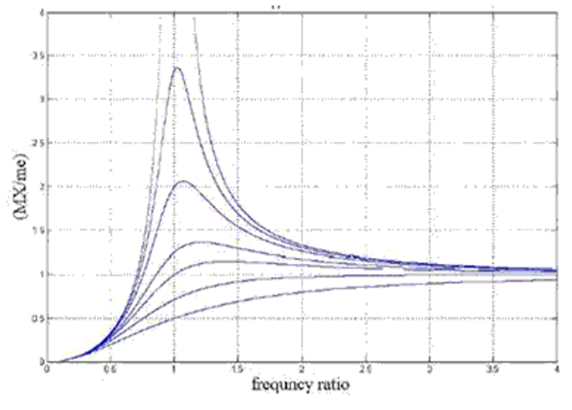
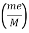– Frequency ratio plot
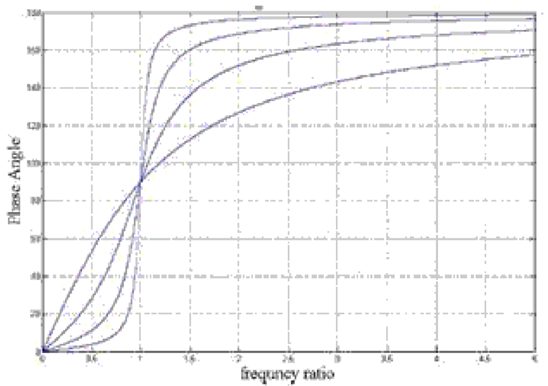
Phase angle – frequency ratio plot
From figure following observations may be made for a rotating unbalanced system
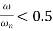
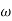
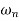
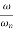
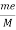
Excitation due to reciprocating unbalance
Consider a reciprocating machine as shown in figure, with M as total mass of system, m as reciprocating mass
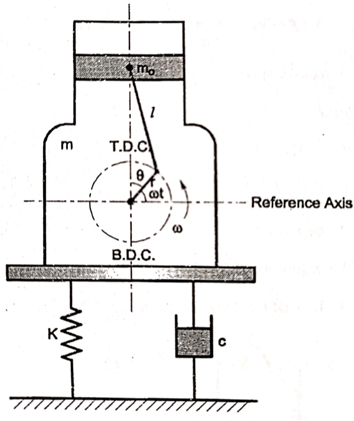
Let,
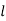= length of connecting rod
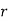= length of crank
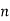= obliquity ratio
The inertia force due to mass of reciprocating parts acts as the excitation force in reciprocating machines. The inertia force due to mass of reciprocating parts are given by,
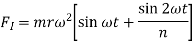
As n is large,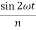 
is very small and can be neglected
From the above equation it is seen that, the exciting force due to reciprocating unbalance is same as due to rotating unbalance.
Hence, analysis of the reciprocating unbalance is same as that of rotating unbalance.
In many cases, the excitation of the system is through the support or base instead of being applied to the mass as shown in figure.
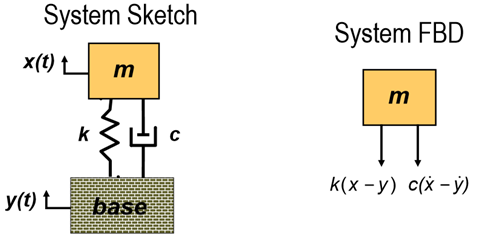
In such condition, the support is considered to be excited by a sinusoidal motion y(t) = y = Y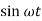 
The analysis of forced vibration due to excitation of support can be done by considering absolute amplitude and relative amplitude of mass w. r. t. support of base.
x(t) = x = X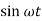 
is absolute displacement of mass
Deflection of spring = x – y
And,
Velocity between two ends of damper =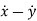 
Where,
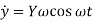
The differential equation is
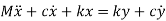
The above equation finally becomes
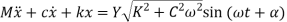
Where,
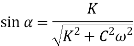
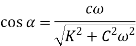
By comparing above equation with equation of forced harmonic vibration
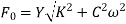
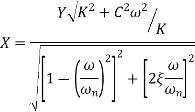
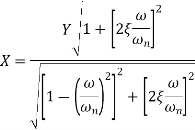
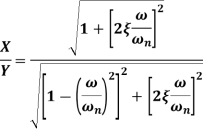
Phase angle = (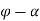
)
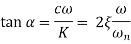
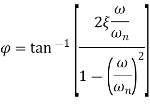
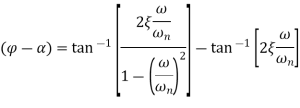
Steady state relative amplitude (Z)
2.5 Magnification Factor
Magnification factor is defined as the ratio of amplitude of steady state vibrations ‘X’ to the zero-frequency deflection ‘Xst’
Where,
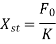
The amplitude X of the steady state forced harmonic vibration is given as
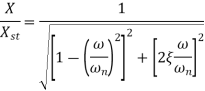
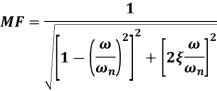
Figure below shows the magnification factor – frequency ratio plot and phase angle – frequency ratio plot.
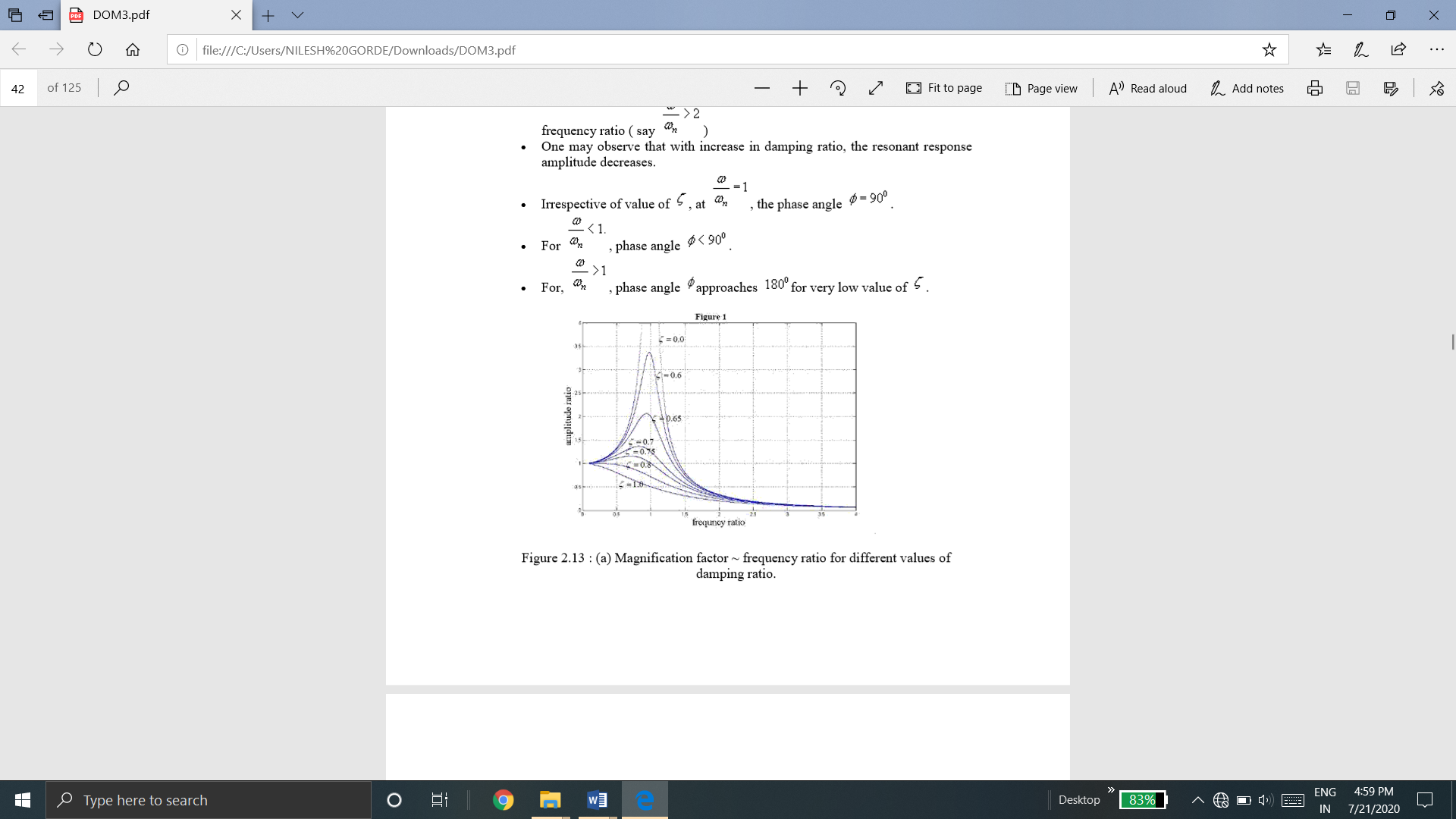
(a) magnification factor – frequency ratio plot
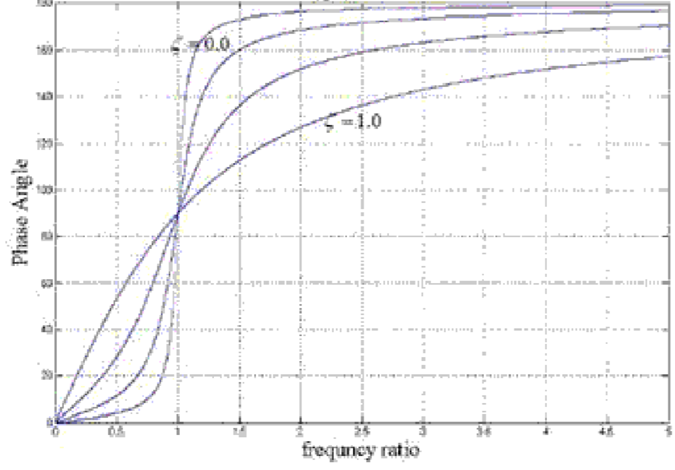
(b) phase angle – frequency ratio plot
Following observation can be made from these plots.
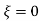
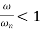
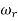
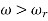
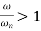
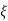
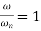
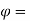
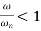
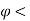
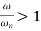
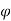
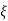
Quality factor
The magnification factor or amplitude ratio of a system at resonance is called as Quality Factor or Q factor of the system
At resonance means,
At, 
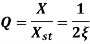
Transmissibility
Force Transmissibility
Force Transmissibility is defined as the ratio of the force transmitted to the supporting structure of foundation Ft to that of force imposed upon the system F0. Force transmissibility measures the effectiveness of the vibration isolating material.
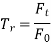
Motion Transmissibility
Motion Transmissibility is defined as the ratio of absolute amplitude X of the mass to the amplitude of the base excitation Y.
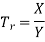
In many industrial applications, one may find the vibrating machine transmit forces to ground which in turn vibrate the neighboring machines. So, in that contest it is necessary to calculate how much force is transmitted to ground from the machine or from the ground to the machine.
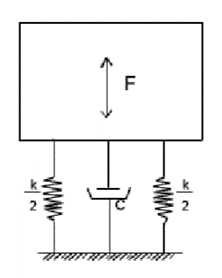
Vibrating system
Figure. shows a system subjected to a force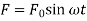 
and vibrating with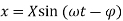
This force will be transmitted to the ground only by the spring and damper.
Force transmitted to the ground
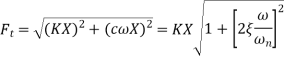
It is known that for a disturbing force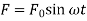 
, the amplitude of resulting oscillation
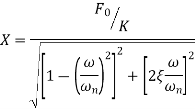
Substituting these equations and defining the transmissibility TR as the ratio of the force transmitted Force to the disturbing force one obtains
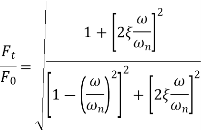
Comparing equations for support motion, it can be noted that
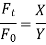
i.e. Mathematically, Force Transmissibility = Motion Transmissibility
When damping is negligible,
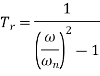
Bandwidth
Fig below shows a response curve of amplitude ratio 
versus frequency ratio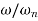 
for values of 
less than 0.1
Let r1 and r2 be the frequency ratio where, the amplitude ratio falls to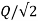 
and are called as half power points.
The difference between the frequencies associated with the half power points is called as bandwidth of the system.
We have,
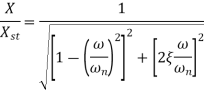
Substituting,
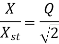
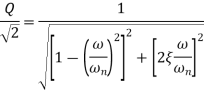
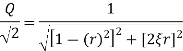
Now,
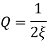
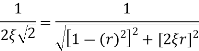
Squaring both sides and solving, we get
For small values of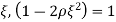 
and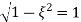 
,
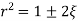
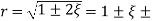higher power terms of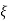 
Neglecting higher power terms
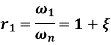
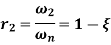
Bandwidth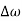 
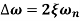
Critical speed of shaft
When rotor is mounted on a shaft its center of gravity usually not coincide with the rotation of the shaft. This C.G. is displaced from axis of rotation although amount of displacement may very slow.
As a result, shaft is subjected to a centrifugal force when it begins rotate. The CF acting radially outward, which make the shaft to bend in the direction of eccentricity of the C.G. This unbalance CF, a shaft start vibrating violently in the direction perpendicular to the axis of the shaft. This phenomenon is known as whirling of shaft.
The speed at which the shaft starts to vibrate violently in the direction perpendicular to the axis of the shaft is known as critical speed.
Consider a vertical shaft having negligible inertia and carrying a single rotor is shown in fig
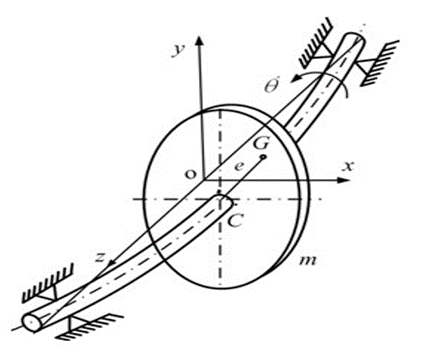
When the shaft is in rotating condition, two forces acts on the shaft
In equilibrium condition, CF = RF
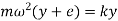
Where,
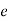= eccentricity of the rotor. i.e. distance between CG and geometric centre.
= deflection of geometric center from the axis passing from O.
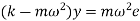
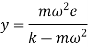
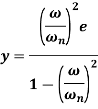
Critical speed is given by
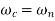
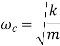
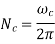
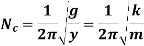
Where,
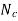= Critical speed of shaft in r.p.s
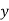= Static deflection of shaft
Ranges of speed
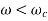
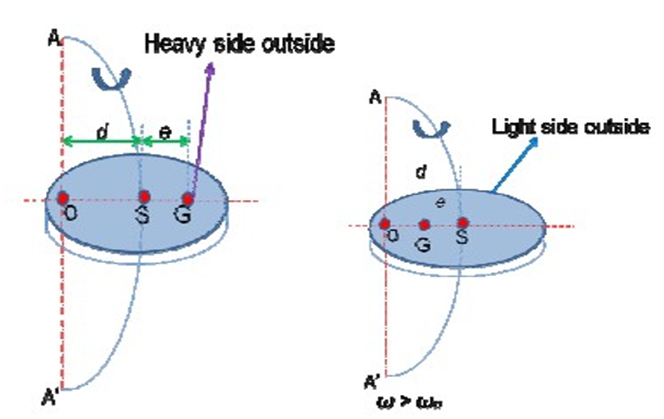
When the speed of shaft is less than the critical speed, then the deflection of shaft is positive.
Deflection of shaft increases with shaft speed. Fig (a)
2. 
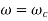
When the speed of shaft is equal to the critical speed, then the deflection of shaft is tending to infinity. This may lead to failure of shaft
3. 
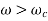
When the speed of shaft is greater than the critical speed, then the deflection of shaft is negative. Fig (b)
References
1. Weaver, Vibration Problems in Engineering, 5th Edition Wiley India Pvt. Ltd, New Delhi.
2. Bell, L. H. and Bell, D. H., Industrial Noise Control – Fundamentals and Applications, Marcel Dekker Inc.
3. Alok Sinha, Vibration of Mechanical System, Cambridge university Press , India
4. Debabrata Nag, Mechanical Vibrations, Wiley India Pvt. Ltd, New Delhi.
5. Kelly S. G., Mechanical Vibrations, Schaums outlines, Tata McGraw Hill Publishing Co.Ltd., New Delhi.
6. Meirovitch, L., Elements of Mechanical Vibrations‖, McGraw Hill.
7. Ver, Noise and Vibration Control Engineering, Wiley India Pvt. Ltd, New Delhi.
8. Bies, D. and Hansen, C., Engineering Noise Control - Theory and Practice, Taylor and Francis.
9. Shrikant Bhave, Mechanical Vibrations Theory and Practice, Pearson, New Delhi
