UNIT 6
Optimum Design
For a design problem a large number of solutions are available which basically fulfil the functional requirement. Optimum design helps to choose the best alternative of the all available keeping a certain target in mind like minimizing weight or maximum strength or minimum cost. Following are the main objectives
Adequate design:
Optimum Design:
The design parameter that make the design complete and successful are classified into three groups
1) Functional requirement parameters:The condition required to be satisfied by mechanical element for which the machine/mechanism has to function satisfactorily.
Characteristics
2) Material Parameters:It describes the material with values.
Characteristics
3) Geometrical parameter:It is defined as the geometry of mechanical element.
Characteristics
Johnson's method involves developing three major design equations and solving these equations. These three equations are
1) Primary design equation (PDE): It is most important equation which outlines the most significant functional requirement to be maximized or the most significant undesirable effect which is to be minimized. For example in design of a tensile bar the primary target of minimum weight, then the equation for weight is the PDE.
2) Secondary design equation (SDE) The secondary or subsidiary design equation are the important equation other than the primary design equation. For example in case of tensile bar design the equation of tensile stress is the SDE.
3) Limit Equation (LE): The limit equations are the important design equation that define the satisfactory ranges of certain design parameters. Like the limiting value of stress, or torsional stiffness etc.
Following steps are followed in optimum design using Johnsons Method for normal specifications
Shear stress
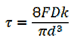
Wahl’s stress factor

Also refer for k value from Data hand book

Where d = diameter of spring wire ‘generally varies from 4 to 12 for general use
Mean coil diameter D = cd
Outer diameter of coil Do= D d
Inner diameter of coil Di= D - d
Axial Deflection
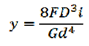
where i = Number of active turns or coils
Where,
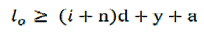
y = Maximum deflection
Clearance ‘a’ = 25% of maximum deflection or a = xdi, for x value refer figure in DHB Assume squared and ground end
∴Number of additional coil n = 2
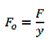
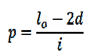
Shafts are designed on the basis of strength or rigidity or both. Design based on strength is to ensure that stress at any location of the shaft does not exceed the material yield stress. Design based on rigidity is to ensure that maximum deflection and maximum twist of the shaft is within the allowable limits.
In designing shafts on the basis of strength, the following cases may be considered:
Shafts Subjected to Torque
Maximum shear stress developed in a shaft subjected to torque is given by,
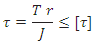
where T = Twisting moment acting upon the shaft,
J = Polar moment of inertia
= 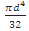 for solid shafts
for solid shafts
= 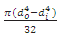 for hollow shafts
for hollow shafts
r= Distance from neutral axis to the outer most fiber = d/2
Shafts Subjected to Bending Moment
Maximum bending stress developed in a shaft is given by,
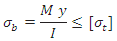
where M = Bending Moment
I = Moment of inertia
=  for solid shafts
for solid shafts
= 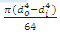 for hollow shafts.
for hollow shafts.
y = Distance from neutral axis to the outer most fiber = d / 2
Shafts Subjected to Combination of Torque and Bending Moment
When the shaft is subjected to combination of torque and bending moment, principal stresses are calculated and then different theories of failure are used. Bending stress and torsional shear stress can be calculated using the above relations.
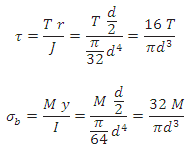
Maximum shear stress is given by,
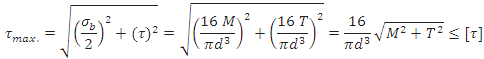
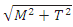 is called equivalent torque, such that
is called equivalent torque, such that

Maximum principal stress is given by,
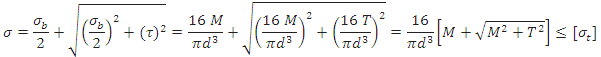
 is called equivalent bending moment, such that
is called equivalent bending moment, such that
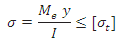
In this section, it is assumed that the cylinder is subjected to only internal pressure. Consider an elemental ring of radius r and radial thickness dr. (sr) and (st) are radial and tangential stresses respectively. Considering the equilibrium of vertical forces
2σtdr + 2(r+dr)(σr+dσr) = 2rσr
Neglecting the term (dr x dσr), the above expression is written as
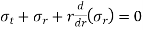 (a)
(a)
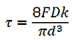
It is further assumed that the axial stress (σ1) is uniformly distributed over the cylinder wall thickness. Therefore, the strain (ε1) isconstant.

 (b)
(b)
where E is the modulus of elasticity and (m) is Poisson’s ratio. The right-hand side of Eq. (b) is constant and is denoted by (–2Cl ).
σr - σt =–2Cl (c)
Adding Eqs. (a) and(c),

Multiplying both sides of the above equation by (r),
 (d)
(d)
Since,
 (e)
(e)
From (d) and (e),

Integrating with respect to r,
 or,
or,
 =
=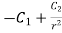 (f)
(f)
Substituting the above value in the Eq. (c),
 =
=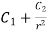 (g)
(g)
The constants C1 and C2 are evaluated from the following two boundary conditions:
 when
when 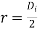
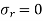 when
when 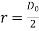
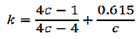


Substituting the constants in Eqs. (f) and (g),

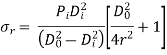
The negative sign is introduced in theexpression for (σr) since it denotes compressivestress.
At the inner surface of the cylinder,

and the stresses are given by,
σr = –Pi
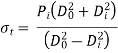
At the outer surface of the cylinder,

and the stresses are given by
σr = 0
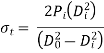
The variation of principal stresses (σr) and (σt) across the cylinder thickness is shown in above fig
The principal stress in axial direction (s1) is assumed to be uniform over the cylinder wall thickness. Considering equilibrium of forces in the axial direction,
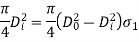

In engineering, redundancy is the duplication of critical components or functions of a system with the intention of increasing reliability of the system, usually in the form of a backup or fail-safe, or to improve actual system performance
The two functions of redundancy are passive redundancy and active redundancy. Both functions prevent performance decline from exceeding specification limits without human intervention using extra capacity.
Passive redundancy uses excess capacity to reduce the impact of component failures. One common form of passive redundancy is the extra strength of cabling and struts used in bridges. This extra strength allows some structural components to fail without bridge collapse. The extra strength used in the design is called the margin of safety.
Eyes and ears provide working examples of passive redundancy.
Active redundancy eliminates performance declines by monitoring the performance of individual devices, and this monitoring is used in voting logic. The voting logic is linked to switching that automatically reconfigures the components. Error detection and correction and the Global Positioning System (GPS) are two examples of active redundancy.
Electrical power distribution provides an example of active redundancy.


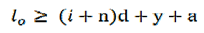
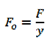
Reference books: