Unit -1
Properties of Fluid
A fluid may be defined as follows:
“A fluid is a substance which is capable of flowing.”
Fluid Mechanics: -
Fluid Mechanics may be defined as that branch of engineering Science which deals with the behavior of fluid under the conditions of rest and motion. The fluid mechanics may be divided into three parts: Statics, Kinematics and dynamics.
Statics: The study of incompressible fluids under static conditions is called hydrostatics and that dealing with the compressible static gases is termed as aerostatics.
Kinematics: It deals with the velocities, accelerations and the patterns of flow only. Forces or energy causing velocity and acceleration are not dealt under this heading.
Dynamics: It deals with the relations between velocities accelerations of fluids with the forces or energy causing them.
A continuous distribution of matter with no voids or empty space is called as continuum.
For mechanical analysis, a fluid is considered to be continuum. Example-water flowing through pipes, channel.
Continuum is based on assumption that fluid is continuous. That is the properties such as density, pressure temperature and velocity are takes to be well defined at infinitely small points and are assumed to vary continuously from one point to another. Air is considered as a continuum.
Density or mass density of a fluid is defined as the ratio of the mass of a fluid to its volume.
It is denoted by the symbol (rho).
The unit of mass density in SI unit is kg/m3.
= Mass of fluid / Volume of fluid = m/v
The value of density of water is 1000 kg/m3
Specific weight or weight density of a fluid is the ratio between the weight of a fluid to its volume.
It is denoted by the symbol w.
w = Weight of fluid / Volume of fluid= W/v
= x g
The value of specific weight or weight density(w) for water is 9810N/m3.
Specific Volume:
Specific Volume of a fluid is defined as the volume of a fluid occupied by a unit mass or volume per unit mass of a fluid is called specific volume.
Mathematically, it is expressed as,
Specific Volume = Volume of Fluid / Mass of Fluid= v/m
= 1/
It is expressed as m3 /kg.
Specific Gravity is defined as the ratio of the weight density of a fluid to the weight density of standard fluid.
Specific gravity is also called relative density. It is dimensionless gravity and is denoted by the symbol S.
S (For Liquids) = Weight density(density) of liquid / Weight density(density) of
Water.
The specific gravity of mercury is 13.6 and specific gravity of water is 1.
Viscosity may be defined as the property of fluid which determines its resistance to shearing stresses. It is a measure of the internal fluid friction which causes resistance to flow.
Viscosity of fluids is due to cohesion and interaction between particles.
du/dy
= du/dy
= Constant of proportionality and is known as co-efficiency of dynamic viscosity.
du/dy = Rate of shear stress or rate of shear deformation or velocity gradient.
We have,
= / [du/dy]
Thus, viscosity may also be defined as the shear stress required to produce unit rate of shear strain.
Units Of Viscosity:
In S.I. units: N.s/m2
Kinematic Viscosity:
Kinematic Viscosity is defined as the ratio between the dynamic viscosity and density of fluid. It is denoted by v (called nu).
v = Viscosity / Density
= /
Units Of Kinematic Viscosity:
In SI units: m2/s
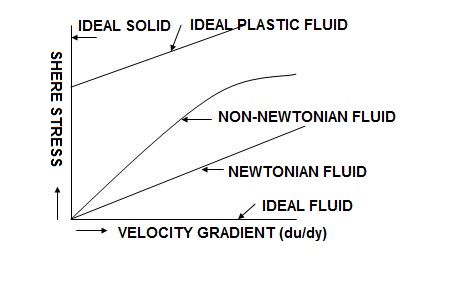
Newton’s Law of Viscosity:
This law states that the shear stress () on a fluid element layer is directly proportional to the rate of shear strain. The constant of proportionality is called the co-efficient of viscosity.
= du / dy
The fluids which follow this law are known as Newtonian fluids.
Ideal Fluid: A fluid which is incompressible and is having no viscosity, is known as an ideal fluid. Ideal Fluid is only an imaginary fluid as all the fluids. which exist have some viscosity.
Real Fluid: A fluid, which possesses viscosity, is known as real fluid. All the fluids in actual practice are real fluids.
Newtonian Fluid: A real fluid, in which the shears stress is directly proportional to the rate of shear strain is known as a Newtonian fluid.
E.g., Water, Kerosine.
Non - Newtonian Fluid: A real fluid, in which the shear stress is not proportional to the rate of shear stain Known as a Non – Newtonian Fluid.
Example Blood, mud.
Ideal Plastic Fluid: A fluid, in which shares stress is more than the yield value and shear stress is proportional to the rate of shear strain is known as ideal plastic fluid.
Cohesion: Cohesion means intermolecular attraction between molecules of same liquid. It enables a liquid to resist small amount of tensile stresses. Cohesion is a tendency of the liquid to remain as one assemblage of particles.
Adhesion: Adhesion means attraction between the molecule of a liquid and the molecule of a solid boundary surface is contact with the liquid. These properties enable a liquid to stick to another body.
1. Rotating cylinder method
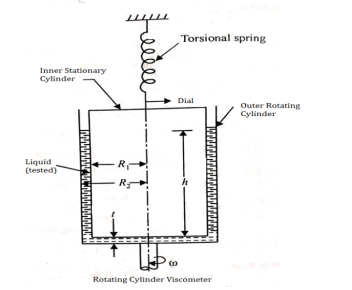
According to Newton’s law of viscosity,
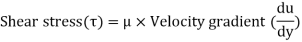
Since the annular space t = (R2 – R1) is quite small (where R2 and R1 are the radii of the outer and inner cylinders respectively), the velocity gradient
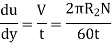
(Where N= the rotational speed of the outer cylinder in rpm)
Shear stress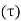
= 
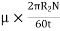
Viscous drag = Shear stress × Area
= 
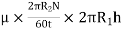
(Where h = height of liquid)
Viscous torque = Viscous drag x radius
=
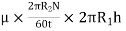x 
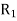
Viscous torque must be equal to the torque T exerted by the torquemeter.
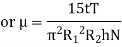
Thus, a rotational type viscometer can be calibrated to directly give u for given speed of rotation N.
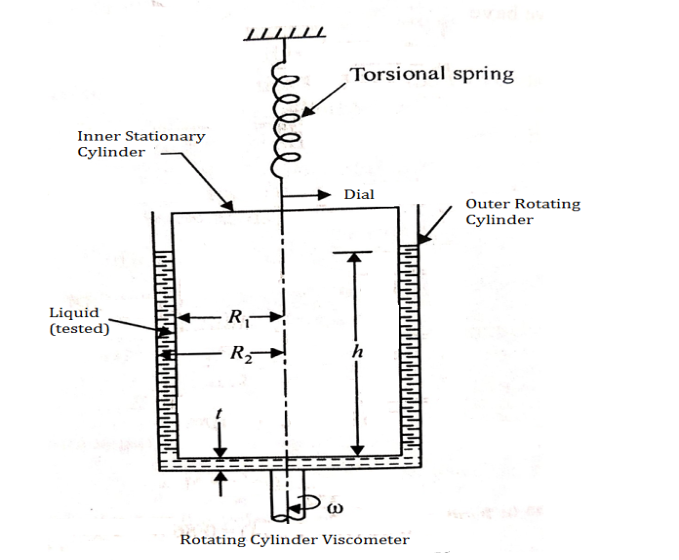
2. Falling Sphere Method
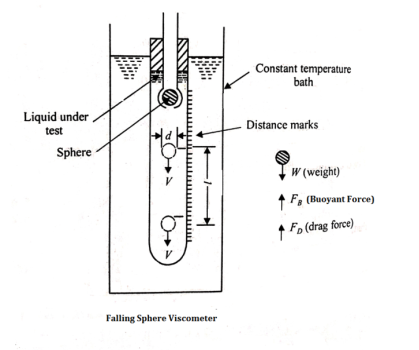
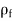
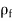
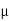
The force acting on the sphere are-
1) Weight W, acting vertically downward.
2) Buoyant force FB, acting vertically upward
3) Drag force FD, acting vertically upward.
W= volume × Density of sphere × g
=
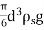
FB = weight of liquid displaced
= volume of liquid displaced × density of liquid × g
=
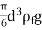
FD = 3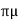
VD
For equilibrium
FD + FB = W
FD = W – FB
3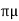
VD =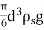 
- 
= 
= 
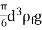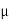From the above eqn the value of dynamic viscosity u can be determined.
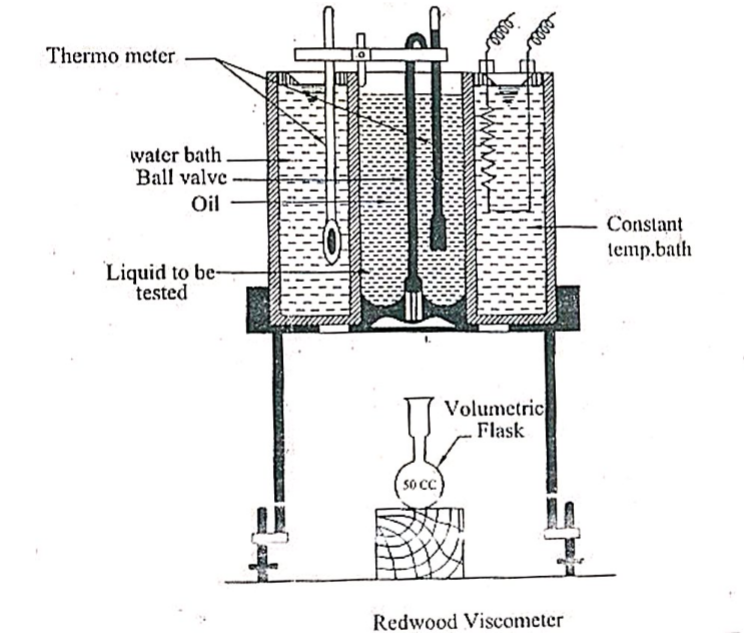
3. Redwood viscometer
1]. Calculate the specific weight, density & specific gravity of one liter of liquid which weighs 7 N
Given
V = 1 lit = 1/1000 = 1 x 10-3 m3,, S
W = 7 N
i). Specific weight = W/V = 7/1 x 10-3 = 7000 N/m3
ii). Density = /g = 7000/9.81 = 713.5 kg/m3
iii). Specific gravity S = /w = 7000/9810 = 0.713
2]. The absolute viscosity of liquid having specific gravity of 0.87 is 0.073 poise. Find kinematic viscosity in m2/s & stoke.
Given
S = 0.87
= 0.073 poise = 0.073/10
= 7.3 x 10-3 Ns/m2
1). Density = S x w
= 0.87 x 1000
= 870 kg/m3
2). Kinematic viscosity = v = / = 7.3 x 10-3 / 870
= 8.39 x 10-6 m2/s
= 8.39 x 10-6/10-4
= 0.0839 stoke
3] A flat plate of area 1.5 x 106 mm2 is pulled with a speed of 0.4 m/s relative to another plate located at a distance of 0.15 mm from it. Find the force & power required to maintain this speed, if the fluid separating them is having viscosity as 1 poise.
Given
A = 1.5 x 106 mm2 = 1.5 m2
du = 0.4 m/s
dy = 0.15 mm = 0.15 x 10-3 m
= 1 poise = 1/10 = 0.1 Ns/m2
1). = du/dy = 0.1 x 0.4/0.15 x 10-3 = 266.67 N/m2
2). F = x A = 266.67 x 1.5 = 400 N
3). Power(P) = F x u
= 400 x 0.4
= 160 watts
4]. Calculate the dynamic viscosity of an oil, which is used for lubrication between a square plate of size 0.8 m x 0.8 m &an inclined plane with angle of inclination 300 as shown in fig. The weight of the square plate is 300 N & it slides down the inclined plane with a uniform velocity of 0.3 m/s. The thickness of oil film is 7.5 mm.
Given
A = 0.8 x 0.8 = 0.64 m2
= 300
W = 300 N
u = 0.3 m/s
dy = 1.5 mm = 1.5 x 10-3 m
1). F = 300Sin = 300 sin30 = 150 N
2). = F/A = 150/0.64 = 234.375 N/m2
3). = du/dy
xdy/du =
234.375 x 1.5 x 10-3/0.3 =
= 1.17 Ns/m2
5]. The dynamic viscosity of an oil, used for lubrication between a shaft & sleeve is 6 poise. The shaft is of diameter 0.4m & rotates at 190 rpm. Calculate the power lost in the bearings for a sleeve length of 90 mm. The thickness of the oil film is 1.5 mm.
Given
= 6 poise = 6/10 = 0.6 Ns/m2
D = 0.4 m
N = 190 rpm
L = 90 mm = 0.09 m
dy = 1.5 mm = 1.5 x 10-3 m
1). u = πDN/60 = π x 0.4 x 190/60 = 3.98 m/s
2). du = u-0 = 3.98 m/s
3). = du/dy = 0.6 x 3.98/1.5 x 10-3 = 1592 N/m2
4). F = x Area
= 1592 x π x D x L
= 1592 x π x 0.4 x 0.09
= 180.05 N
5). Torque = F x D/2 = 180.05 x 0.4/2 = 36.01 Nm
6). Power lost = 2πNT/60 = 2π x 190 x 36.01/60 = 716.48 W
6]. Two large plane surfaces are 2.4 cm apart. The space between the surfaces is filled with glycerin. What force is required to drag a very thin plate of surface area as square meter between the two large plane surfaces at a speed of 0.6 m/s if,
i). The thin plate is in the middle of the two plane surfaces.
ii). The thin plate is at a distance of 0.8 cm from one of the plane surfaces?
Take = 8.10 x 10-1 Ns/m2
Given:
A = 0.5 m2
u = 0.6 m/s
= 8.10 x 10-1 Ns/m2
Case 1. When the thin plate is in the middle of the two planes.
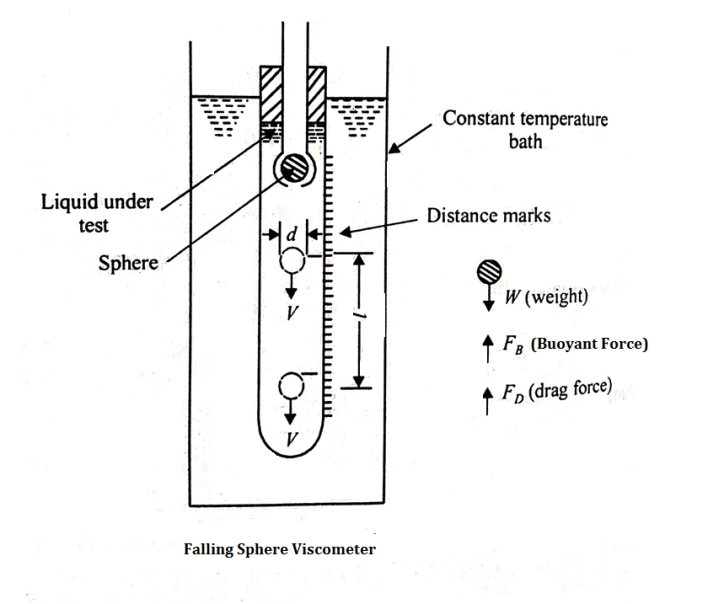
dy = 0.024/2 = 0.012 m
= du/dy
= 8.10 x 10-1 x 0.6/0.012 = 40.5 N/m2
F = x A x 2
= 40.5 x 0.5 x 2
= 40.5 N
ii). When the thin plate is at a distance of 0.8 cm from one of the planes.
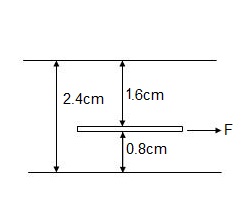
dy1 = 0.008 m
dy2 = 0.024 – 0.008 = 0.016 m
1 = du/dy1 = 8.10 x 10-1 x 0.6/0.008
= 60.75 N/m2
F1 = 1 x A = 60.75 x 0.5 = 30.375 N
2 = du/dy2 = 8.10 x 10-1 x 0.6/0.016
= 30.375 N/m2
F2 = 2 x A = 30.375 x 0.5 = 15.187 N
F = F1 + F2
= 30.375 + 15.187
= 45.562 N
7] A vertical gap 2.2 cm wide of infinite extent contains a fluid of viscosity 2 Ns/m2& sp.gr 0.9. A metallic plate 1.2m x 1.2m x 0.2cm is to be lifted up with a constant velocity of 0.15 m/sec, through the gap. If the plate is in the middle of the gap. Find force required.
The weight of the plate is 40N.
Width of gap = 2.2 cm = 0.022 m
= 2 Ns/m2
S = 0.9
= S x 9810 = 0.9 x 9810
= 8829 N/m3
Size of plate = (1.2 x 1.2 x (2 x 10-3)) m
du = 0.15 m/sec
Weight of plate = 40 N
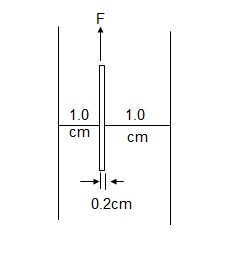
1). Distance of plate from vertical surface of the gap, when plate is in the middle.
dy = 0.022 – 2 x 10-3/2 = 0.01 m
2). = x du/dy = 2 x 0.15/0.01 = 30 N/m2
3). Total shear force = 2 x x A
F = 2 x 30 x (1.2 x 1.2)
= 86.4 N
4). The upward thrust = weight of fluid displaced
= x v
= 8829 x 1.2 x 1.2 x 2 x 10-3
= 25.43 N
5). Effective weight of= weight of plate – Upward thrust
the plate
= 40 – 25.43
= 14.57 N
6). Total force required to = F + 14.57
lift the plate up
= 86.4 + 14.57
= 100.97 N
8] Using Buckingham’s Π theorem, show that velocity through circular orifice is given by
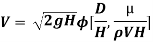
Where H= Head causing flow
D = Diameter of orifice
µ = co-efficient of viscosity
ρ = Density
Solution: V is the function of H, D, µ, ρ, and g
Mathematically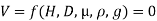 
Or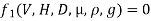 
Total number of variables n = 6
Writing dimensions of each variable
V = LT-1, H = L, D = L, µ = ML-1T-1, ρ = ML-3, g = LT-2
No. of fundamental dimensions m = 3
No of Π terms = n-m = 6-3 = 3
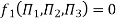
Each Π term contains (m+1) variables where m=3 and is also equal to repeating ‘variables. Choosing H, g, ρ as repeating variables.
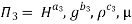
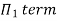
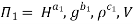
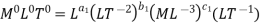
For M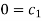 
For L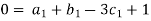 
For T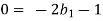 
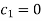and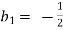 
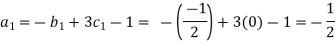
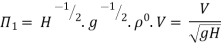
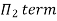
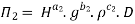
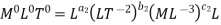
For M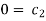 
For L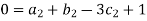 
For T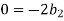 
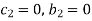
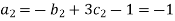
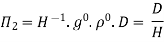
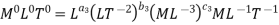
For M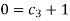 
For L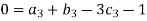 
For T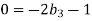 
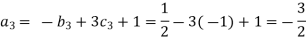
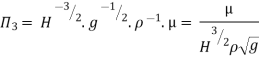
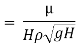
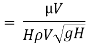
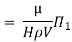
Substituting the values of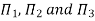 
in equation 1
Or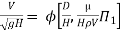 
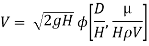
9] The discharge Q of a centrifugal pump depends upon the mass density of fluid (ρ), the speed of the pump (N), the diameter of the impeller D, the manometric head Hm and the viscosity of fluid µ. Show that
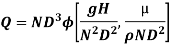
Solution: The discharge Q is function of N, g, D, H, µ, ρ.
Mathematically,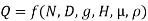 
Or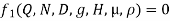 
Total number of variables n = 7
Q = L3T-1, N = T-1, D = L, g = LT-2, H = L, µ = ML-1T-1, ρ = ML-3
No. of fundamental dimensions m =3
Number of Π terms = n – m = 7 – 3 = 4
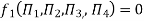-------- 1
Each Π term contains (m+1) variables where m =3 and also equal to repeating variables. Choosing D, N, ρ as repeating variables.
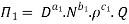
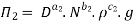
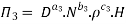
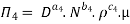
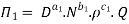
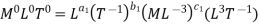
For M 
For L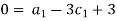 
For T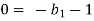 
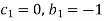
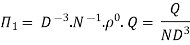
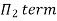
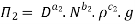
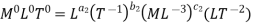
For M 
For L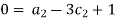 
For T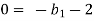 
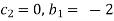
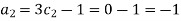
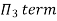
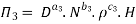
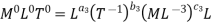
For M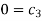 
For L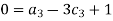 
For T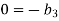 
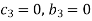
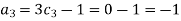
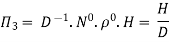
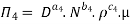
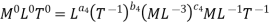
For M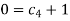 
For L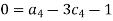 
For T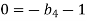 
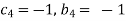
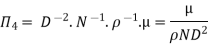
Substituting the values of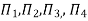 
in equation 1
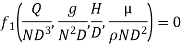
As the product of two Π – terms are also dimensionless, the terms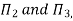 
can be replaced by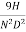 
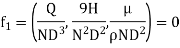
Or 
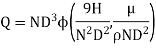
Lubricant fluids are liquid mixtures typically used for lubrication, protection, friction reduction and cooling of metal surfaces belonging to mechanical gears in operation. These mixtures are composed of a base oil of hydrocarbon nature in which a variety of additives are dissolved (e.g., mineral or synthetic additives). Lubricating oils used in vehicles are also identified with the name of "motor oils".
For a first look at how fluids behave when they are deformed, here is an experiment you could attempt on your own kitchen table. Arrange two horizontal parallel plates, spaced a distance LL apart, with a fluid at rest between them. You could justifiably argue that it would be hard to make such an experiment, because how could you keep the fluid from leaking out at the margins of the plates? Do not worry about such practicalities; just suppose that the plates are very broad relative to their spacing, or that the fluid you have chosen is “thick”, i.e., has a high viscosity (you are likely to have a number of high- viscosity household fluids, like honey, or molasses, or corn syrup, or motor oil, available), which would ooze out from the between the plates only slowly, giving you time to do the experiment described below.
Fig. Shearing a fluid between two parallel plates.
Accelerate the upper plate rapidly to a constant velocity V parallel to itself by applying a force per unit area, call it F, over its entire surface, while you hold the lower plate fixed by applying to it an equal and opposite force per unit area. You could do that by taping the lower plate to the table and attaching handles with suction cups to the top of the upper plate. The fluid is set in motion by friction from the moving plate.
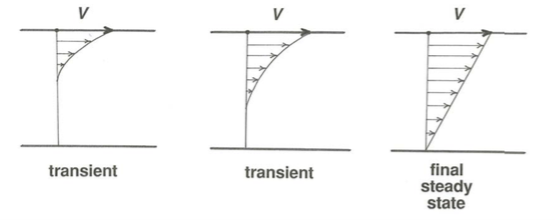
Figure Development of the velocity profile in a fluid sheared between two parallel plates. From Figure you can see that the fluid in contact with each of the plates has exactly the same velocity as the plates themselves. This is a manifestation of what is known as the no-slip condition: fluid in contact with a solid boundary has exactly the same velocity as that boundary. Although this no- slip condition might seem counterintuitive to you, it is a fact of observation, and it can be justified by considerations on intermolecular forces. The flow of the continuously deforming fluid past the solid boundary is not the same as sliding a rigid slab, like a brick, across a table top. Intermolecular forces act between the fluid and the solid at the boundary just as they do across planes of shearing in the interior of the fluid, so there’s no more reason to expect a discontinuity in velocity at the boundary than within the fluid.
Surface tension is caused by the force of cohesion at the free surface.
A liquid molecule in the interior of the liquid mass is surrounded by the other molecules all around and is in equilibrium.
At the free surface of the liquid, there are no liquid molecules above the surface to balance the force of the molecules below it.
Consequently, as shown in fig there is net inward force on the molecules at the free surface.
The force is normal to the liquid surface.
At the free surface a thin layer of molecules is formed.
It is denoted by letter .
Its SI unit is N/m.
Capillarity is defined as a phenomenon of rise or fall of a liquid surface in small tube relative to the adjacent general level of liquid when the tube is held vertically in the liquid.
The rise of liquid surface is known as capillary rise while the fall of the liquid surface is known as capillary depression.
It is expressed in terms of cm or mm of liquid.
Its value depends upon the specific weight of the liquid, diameter of the tube and surface tension of the liquid.
h =Height of the liquid in the tube.
d = Diameter of tube
= Surface tension of liquid.
= Angle of contact between liquid and glass tube.
= Density Of liquid.
h= 4cos / e*g*d.
Compressibility The property by virtue of which fluids undergo a change in volume under the action external pressure is known as compressibility. It decreases with the increase in pressure of fluid.
References:
1. Kundu, Cohen, Dowling, “Fluid Mechanics”, Elsevier India
2. Chaim Gutfinger David Pnueli, “Fluid Mechanics” Cambridge University press.
3. Edward Shaughnessy, Ira Katz James Schaffer, “Introduction to Fluid Mechanics”, Oxford University Press
