UNIT 2

Kinematic Analysis of Mechanisms: Analytical Method

2.1           Position analysis of a slider-crank mechanism

A position analysis of a slider-crank mechanism is shown here exploitation analytical methodology. The pure mathematics equations obtained through pure mathematics relationship were solved for unknown joint angles or values. These results enable one to search out the position and therefore the orientation of every link. The language accustomed outline the links and angles are shown in Figure. 2.1.

Figure 2.1 Position Analysis of the slider-crank mechanism

Consider the mechanism to possess links named Link one, Link a pair of and Link three, and having link position vectors 𝐫𝟏, 𝐫𝟐, and 𝐫𝟑 having magnitudes r1, r2, and r3 severally. The slider is known as Link four that is connected to the bottom link, i.e., Link 1, through a prismatic joint and is liberal to endure reciprocal motion. Slider Link, four has AN offset from the bottom Link one whose vector is 𝐫𝟒 with magnitude r4. Let the input crank angle be 𝜃2 and also the remainder of the angles square measure shown within the figure. The vector loop equation is given by,

𝒓𝟐+𝒓𝟑=𝒓𝟏+𝒓𝟒 (1)

Equation (1) can be arranged in the components form as

𝑟2cos𝜃2+𝑟3cos𝜃3=𝑟1 (2)

𝑟2sin𝜃2+𝑟3sin𝜃3=𝑟4 (3)

From Equation (3), the orientation of Link 3 can be obtained as

𝜃3=sin−1𝑟4−𝑟2sin𝜃2𝑟3 (4)

The Slider (Link 4) position can be found using Equation (2) as

𝑟3=𝑟1−𝑟2cos𝜃2cos𝜃3 (5)

After calculating 𝜃3 and 𝑟3, an equivalent position diagram can be drawn which is shown in Figure 2.2.

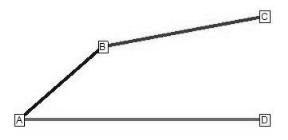
Figure.2.2. Vector diagram for the position of slider-crank mechanism

Key Takeaways:

A position analysis of slider-crank mechanism, calculation of the position in slider-crank mechanism.

2.2           Velocity analysis of the slider-crank mechanism

In the graphical technique, the orientation of every link obtained from the position analysis is employed for the rate analysis. If a link features a motion with reference to the other link, the direction of motion of the link and thus its speed vector is going to be perpendicular to the link. On the opposite hand, if the motion is translatory, the direction of its speed vector is going to be in the direction of the motion. within the case of the slider-crank mechanism at hand, a vector for Link two (crank) is drawn on an appropriate scale that magnitude of speed and direction area unit well-known from the input parameters. The direction of the rate vector of Link three i.e., rod, is perpendicular thereto. The direction of the speed vector of Link four (slider) is on its translatory motion. The point may be determined for these 2 directions and thus a vector plane figure is obtained. Sides of the plane figure represent speed vectors that correspond to the direction of the rate, and by mapping its magnitude to the initial scale, the linear speed of the links area unit is calculated. additional data on the graphical ways may be found in the next unit. For the implementation of the Mech analyzer, the magnitude of the linear speed at the terminus of every link resolves to urge the rate plane figure. Product of the magnitude of angular speed and also the length of the link provides the linear speed of the top purpose of every link. concerning Figures.2.3, let the angular speed of Link two be 𝜔2 and its length be 𝑟2 (≡|𝐀𝐁⃗|). The linear speed of purpose B with reference to purpose A can be:

𝑣2= 𝜔2 𝑟2 (6)

First draw speed vector 𝐚𝐛⃗⃗⃗⃗⃗ for Link two (Figure 6) traditional to AB (Figure 5) with a magnitude as 𝑣2. Now, draw the rate traditional to 𝐁𝐂⃗⃗⃗⃗⃗ and 𝐃𝐂⃗, severally, so as to get the rate polygonal shape. Note purpose|that time} D is drawn continuously below point C. Magnitudes of 𝐛𝐜⃗⃗⃗⃗ and 𝐝𝐜⃗⃗⃗⃗ area unit up to the linear speed of Link three and Link four, severally. speed vector diagram obtained during this means for a slider-crank mechanism is shown in Figure six. Let the angular speed for Link three be 𝜔3 with its length as 𝑟3 (≡|𝐁𝐂⃗⃗⃗⃗⃗ |). The angular speed is then given by

𝜔3= |𝒃𝒄⃗⃗⃗⃗ |𝑟3 (7)

The linear velocity of Link 4 (slider) can be obtained as

𝑣4=|𝒅𝒄⃗ | (8)

Figure.2.3. Velocity vector diagram for the slider-crank mechanism

ACCELERATION ANALYSIS OF THE SLIDER-CRANK MECHANISM

In the case of the acceleration analysis, there are two components of the linear acceleration of each link. They are radial and tangential. Let a2^r and a2^t be radial and tangential components of acceleration respectively for link 2. Angular acceleration 𝛼2 of Link 2 will be taken as the input from the user. Its radial and tangential components are determined using,

                                       a2r=w2 r2 (9)

                                       a2t= a2r2 (10)

So the resultant acceleration of Link 2 can be obtained as,

𝑎2=√ ((𝑎2𝑟2)2+ (𝑎2𝑡2)2) (11)

Link 4 (slider) has only linear velocity so it will have only a tangential acceleration component. The radial acceleration component for Link 3 will be:

𝑎3𝑟=𝜔32𝑟3 (12)

The implementation of the acceleration vector diagram is shown in Figure 2.4.

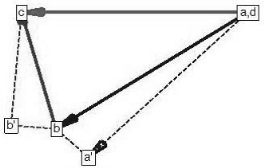
Figure.2.4. Acceleration diagram for the mechanism

First draw speed vector 𝐚𝐛⃗⃗⃗⃗⃗ for Link two (Figure 6) traditional to AB (Figure 5) with a magnitude as 𝑣2. Now, draw the rate traditional to 𝐁𝐂⃗⃗⃗⃗⃗ and 𝐃𝐂⃗, severally, so as to get the rate polygonal shape. Note purpose that time} D is drawn continuously below point C. Magnitudes of 𝐛𝐜⃗⃗⃗⃗ and 𝐝𝐜⃗⃗⃗⃗ area unit up to the linear speed of Link three and Link four, severally. speed vector diagram obtained during this means for a slider-crank mechanism is shown in Figure six. Let the angular speed for Link three be 𝜔3 with its length as 𝑟3 (≡|𝐁𝐂⃗⃗⃗⃗⃗ |). The angular speed is then given by

𝑎3= |𝐛𝐜⃗ | (14)

Key Takeaways:

Velocity analysis, ways of finding out the velocity of slider-crank mechanism,

acceleration analysis, resultant acceleration, velocity, and acceleration diagram.

2.3           Velocity and Acceleration Analysis of Four-Bar and Slider crank mechanisms using Vector and Complex Algebra Methods

2.3.1 Velocity and Acceleration by Complex Algebra Method

Using the slider-crank of Fig. 2.6. once more as an illustration with an x-axis along the

the centerline of the guide, and recalling that i^2=-1, we write the complex-number

equations as follows, with the equivalent vector equation below each:

Displacement:              ae^ia + be^ib+ce^ic=x        ……. (1) 

                                                    AB + BD + DC = AC           ……(2)

Velocity:                                iae^iawAB + (ibe^ib + ice^ic) +BC = dx/dt   …. (3)

VB +VD/B +VC/D=VC……..(4)

Note that wAB =da/dt is positive when counter-clockwise and negative when clockwise; in this problem wAB is negative.

The complex conjugate of Eq. (3)

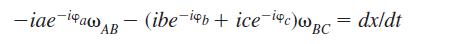
From Eqs. (3) and (4), regarded as simultaneous equations:

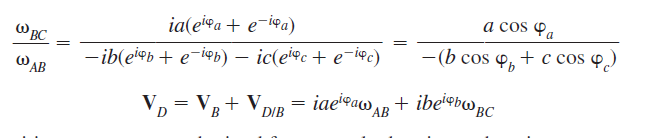
The quantities a, b, c square measure obtained from a scale drawing or by trig. Both the vector-polygon and therefore the complex-number ways is without delay extended to accelerations, additionally the} latter also to the upper accelerations.

Differentiating equation 3 we get,

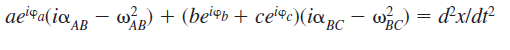
This is equivalent to the vector equation:

Combining the above equation and its complex conjugate, eliminate d^2x/dt^2 and solve for 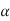BC in the following equation for AD:

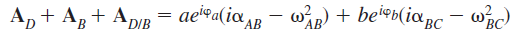
The higher than complex-number approach conjointly lends itself to the analysis of motions involving Coriolis acceleration. The latter is encountered within the determination of the relative acceleration of 2 outright coincident points on totally different links.

2.3.2 Velocity and Acceleration Analysis by Vector Method

The method is illustrated using a point D on the connecting rod of a slider-crank

mechanism (Fig. 2.5). The vector-velocity equation for C is

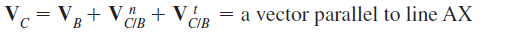
Where VB = velocity of B

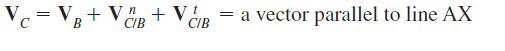
Where Vc= velocity of C

   Vb= velocity of B

Figure.2.6. Velocity – Vector Diagram

We continue with the slider-crank of Fig. 2.5. After solving for the velocities via the

velocity polygon, write out and “draw” the acceleration equations. Again, proceed in order of increasing difficulty: from B to C to D, and determine first the acceleration of point C:

Now, we can draw the acceleration diagram,

1. Choose an arbitrary origin o, as before.

2. Draw each acceleration of scale ka (inch per second squared), and label the appropriate vector terminals with the lowercase letter corresponding

to the point whose acceleration is designated, e.g., AB = (ob)/ka.

Draw ABn, ABt, Ac/B.

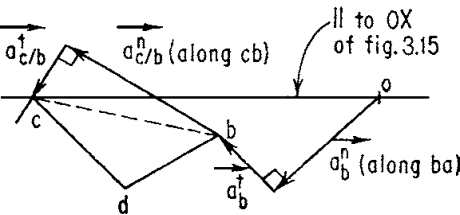
Figure.2.7. Acceleration vector Diagram

Key Takeaways:

Velocity and acceleration analysis of slider-crank chain mechanism by complex

algebra method and vector method, calculation, and analysis, understanding of

concepts.

2.4           Computer-Aided Analysis of Slider Crank and Four bar Mechanism

The sort of machine technique is as giant because of the variety of mechanisms. For specific mechanisms, like cams and gears, specialized codes are on the market. In general, pc codes are capable of analyzing each straightforward and sophisticated mechanism. As way as synthesis is bothered the case is difficult by the nonlinearity of the motion parameters in several mechanisms and by the impossibility of limiting most motions to little displacements. For easier mechanisms, synthesis codes are on the market. For a lot of advanced mechanisms parameter variation of study codes or heuristic, ways are in all probability the foremost powerful presently on the market tools. the topic remains underneath intensive development, particularly with reference to interactive lighting tricks [for example, CADSPAM, software of spatial mechanisms. At high speeds, the inertia forces related to the moving links cause shaking forces and moments to be transmitted to the frame. equalization will cut back or eliminate these. Three-dimensional mechanisms also are referred to as “spatial mechanisms.” Points on these mechanisms travel three-dimensional curves. the fundamental three- dimensional mechanisms are the “spherical four-bar mechanisms” (Fig. 2.8) and therefore the “offset” or “spatial four-bar mechanism” (Fig. 2.9.). The spherical four-bar mechanism of Fig. 2.9. consists of links AB, BC, CD, and DA, every on a good circle of the sphere with center O; turning joints at A, B, C, and D, whose axes meet at O; lengths of links measured by great-circle arcs or angles atomic number 83 subtended at O. Input _2, output _1; the single degree of freedom, though. Figure 2.9. shows a spatial four-bar mechanism; turning joint at D, turn-slide (also referred to as cylindrical) joints at B, C, and D; aij denote minimum distances between axes of joints; input = two at D; output at A consists of translation s and rotation ø1; Σfi=7; freedom, F = 1. Three-dimensional mechanisms utilized in apply are typically special cases of the above 2 mechanisms. Among these are Hooke’s joint,

   is further explained in other units.

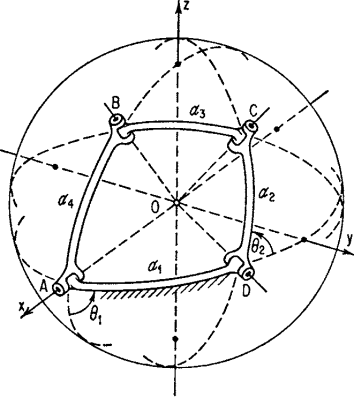
Figure.2.8. Spherical four-bar Mechanism

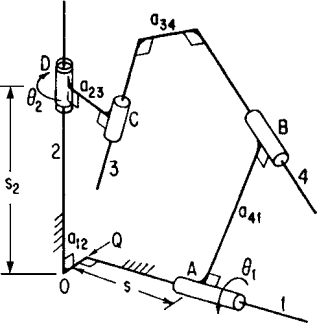
Figure.2.9. Spatial or four-bar Mechanism

Key Takeaways:

Computer-aided analysis of slider-crank and four-bar mechanism, Spherical four-bar mechanism, spatial or four-bar mechanism. Analysis with the help of designing

software.

2.5           Analysis of Single and Double Hooke’s Joint

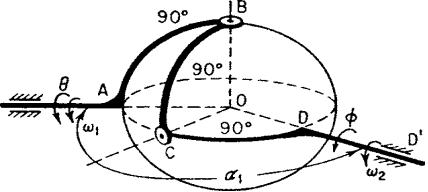
Figure.2.10 Hooke’s Joint

Key Takeaways:

Analysis of Hooke’s joint, calculation of angular velocity ratio, and its types.

Reference Books:

3.     Paul E. Sandin, “Robot Mechanisms and Mechanical Devices Illustrated”, Tata McGraw Hill Publication

4.     Ghosh Malik, “Theory of Mechanism and Machines”, East-West Pvt. Ltd.

5.     M.P. Groover, “Automation, production systems, and computer-integrated manufacturing”, Prentice-Hall of India Pvt. Ltd