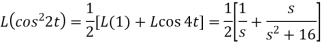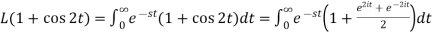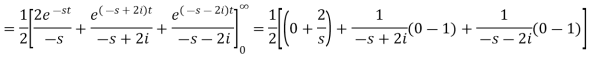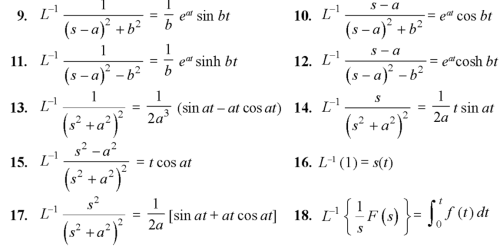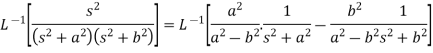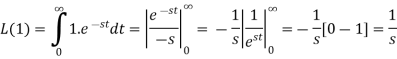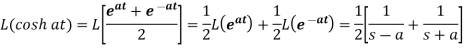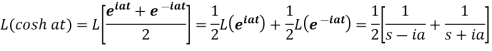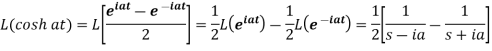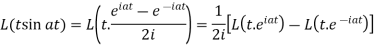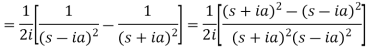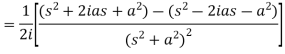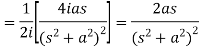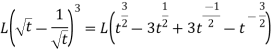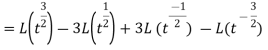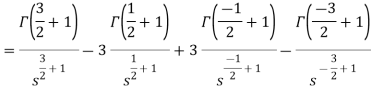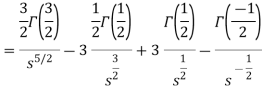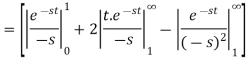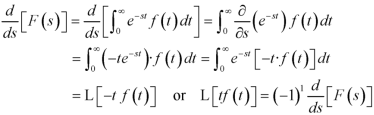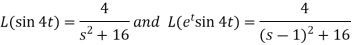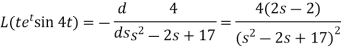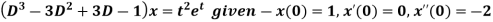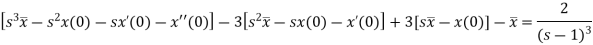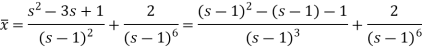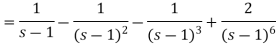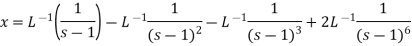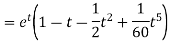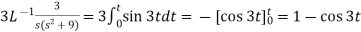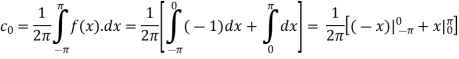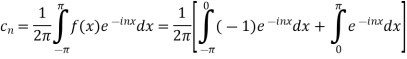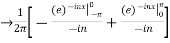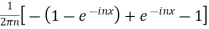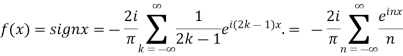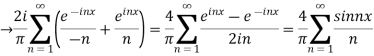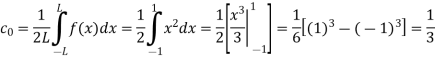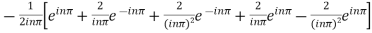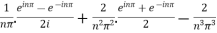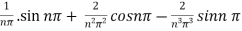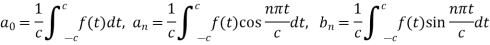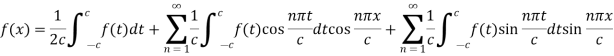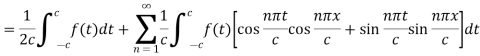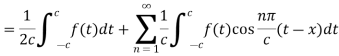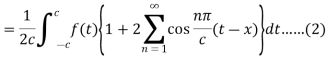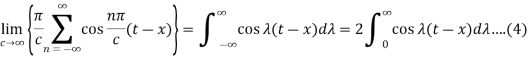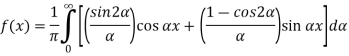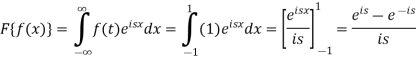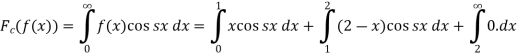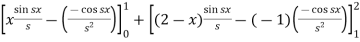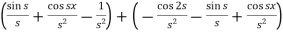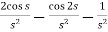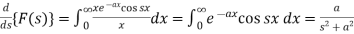Unit-2
Transforms
Let f(t) be any function of t defined for all positive values of t. then the Laplace transform of the function f(t) is defined as-
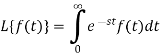
Provided that the integral exists, here ‘s’ is the parameter which could be real or complex.
The inverse of the Laplace transform can be defined as below-
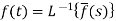
Here 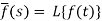
f(t) is called the inverse Laplace transform of 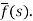
L is called the Laplace transformation operator.
Conditions for the existence of Laplace transforms-
The Laplace transform of f(t) exists for s>a, if
1. f(t) is a continuous function.
2.  is finite.
is finite.
Important formulae-
1. 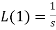
2. 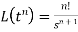
3. 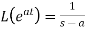
4. 
5. 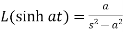
6. 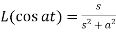
7. 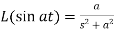
Example-1: Find the Laplace transform of the following functions-
1. 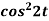 2.
2. 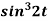
Sol. 1.
Here 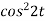
So that we can write it as-
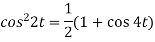
Now-
|
2. Since 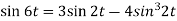
Or 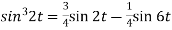
Now-
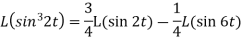
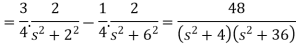
Example-2: Find the Laplace transform of (1 + cos 2t)
Sol. |
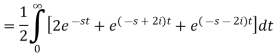
|
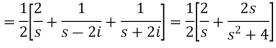
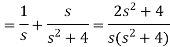
So that-
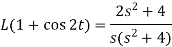
Inverse Laplace transforms-
The inverse of the Laplace transform can be defined as below-
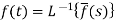
Here 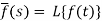
f(t) is called the inverse Laplace transform of 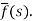
L is called the Laplace transformation operator.
Important formulae-
1.  2.
2. 
3. 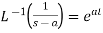 4.
4. 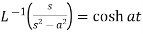
5. 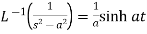 6.
6. 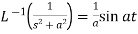
7. 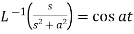 8.
8. 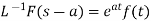
|
Example: Find the inverse Laplace transform of the following functions-
1. 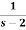
2. 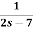
Sol.
1.
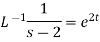
2.
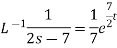
Example: Find the inverse Laplace transform of-
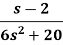
Sol.
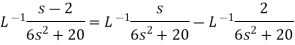
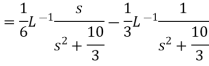
|
Multiplication by ‘s’ -

Example: Find the inverse Laplace transform of-
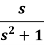
Sol.

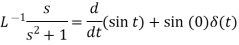

Division by s-

Example: Find the inverse Laplace transform of-
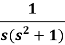
Sol.
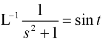
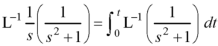
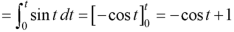
Inverse Laplace transform of derivative-
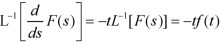
Example: Find 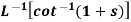
Sol.
|
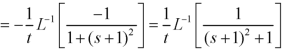
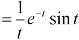
Inverse Laplace transform by using partial fraction
We can find the inverse Laplace transform by using partial fractions method described below-
Example: Find the Laplace inverse of-
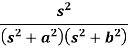
Sol.
We will convert the function into partial fractions-
|
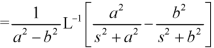
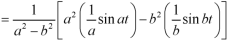
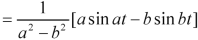
Example: Find the inverse transform of-
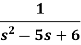
Sol.
First we will convert it into partial fractions-
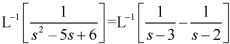
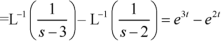
Inverse Laplace transform by convolution theorem-
According to the convolution theorem-
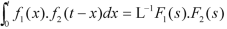
Example: Find
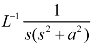
Sol.
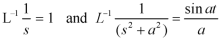
Therefore by the convolution theorem-
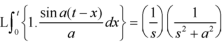

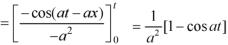
LT of standard functions-
1. 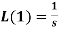
Proof: by the definition of Laplace transform-
|
So that-
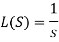
2. 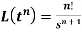
Proof: by the definition of Laplace transform-
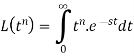
Let 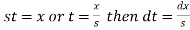
So that-
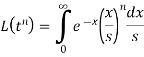
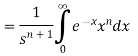
We know that-

Then-

3.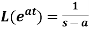
Proof: by the definition of Laplace transform-
|
|
4. 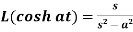
Proof: here we know that,
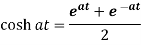
So that-
|
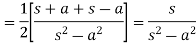
5. 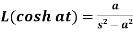
Proof: here we know that,
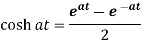
So that-
|
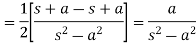
6. 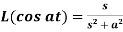
Proof: here we know that,
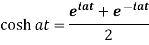
So that-
|
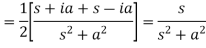
7. 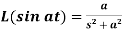
Proof: here we know that,
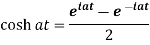
So that-
|
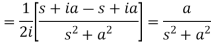
Key takeaways-
- The Laplace transform of the function f(t) is defined as-

2. The Laplace transform of f(t) exists for s>a, if
- f(t) is a continuous function.
2. 2. 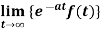 is finite
is finite
3. The inverse of the Laplace transform can be defined as below-

4. Multiplication by ‘s’ -
5. 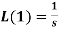
6. 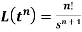
7. 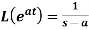
8. 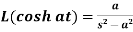
9. 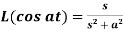
10. 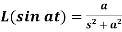
Properties and theorems of LT
1. Linearity property-
Let a and b be any two constants and  ,
,  any two functions of t, then-
any two functions of t, then-
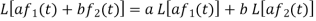
Proof: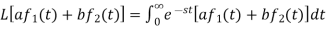

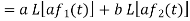
Hence proved.
2. First shifting property (Theorem)- If 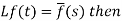
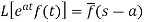
Proof: By definition-
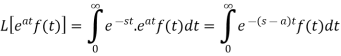
Let (s – a) = r
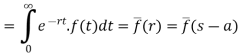
Hence proved.
We can find the following results with the help of the above theorem-
1. 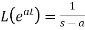
2. 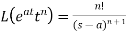
4. 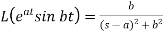
5. 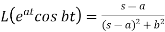
6. 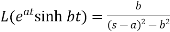
7. 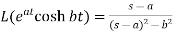
Here s>a in each case.
Example-1: Find the Laplace transform of t sin at.
Sol. Here-
|
Example-2: Find the Laplace transform of 
Sol. Here-
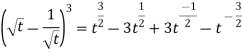
So that-
|
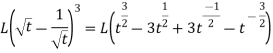
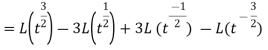

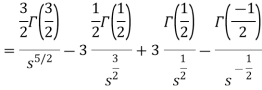
As we know that- 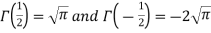
So that-

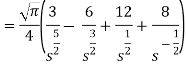
Hence-

Example-3: Find the Laplace transform of the following function-
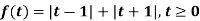
Sol. The given function f(t) can be written as-
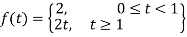
So that, by definition,
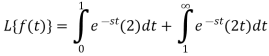
|
Existence theorem-
The Laplace transform of f(t) exists for s>a if –
- F(t) is continuous
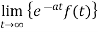 is finite.
is finite.
The above conditions are not necessary but sufficient.
Laplace transforms of derivatives and integrals
Laplace transform of the derivative of f(t)-
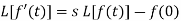
Here 
Proof: by the definition of Laplace transform-
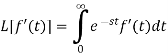
On integrating by parts, we get-
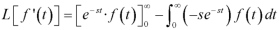
Since 
Then-

So that-
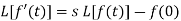
Laplace transform of integral of f(t) -
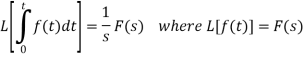
Proof: Suppose
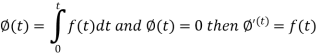
We know that-
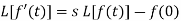
So that-
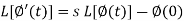
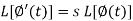
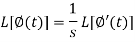
Putting the values of 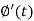 and
and 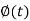 , we get-
, we get-
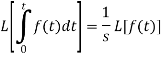
Laplace transform of the function 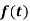 multiplied by t
multiplied by t
If 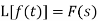 , then-
, then-
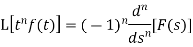
Proof: 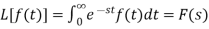
Differentiate w.r.t. x, we get-
|
Similarly-
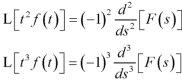
And
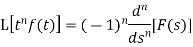
Example-4: Find the Laplace transform of 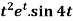 .
.
Sol. Here-
Now-
|
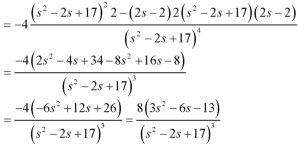
Key takeaways-
- Laplace transform of the function f(t) is defined as-
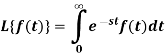
2. Conditions for the existence of Laplace transforms-
The Laplace transform of f(t) exists for s>a, if
1. f(t) is a continuous function.
2. 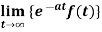 is finite.
is finite.
3. Linearity property-
Let a and b be any two constants and 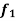 ,
,  any two functions of t, then-
any two functions of t, then-
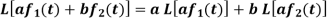
4. First shifting property (Theorem)- If 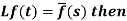
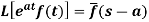
5. Laplace transform of the derivative of f(t)-

Here 
6. Laplace transform of integral of f(t) -

7. Laplace transform of the function 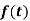 multiplied by t
multiplied by t
If 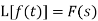 , then-
, then-
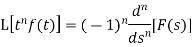
Step by step procedure to solve a linear differential equation by using Laplace transform-
1. Take Laplace transform of both sides of the given differential equation.
2. Transpose the terms with negative sign to the right.
3. Divide by the coefficient of 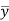 , getting
, getting 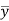 as a known function of s.
as a known function of s.
4. Resolve the function of s into partial fractions and take the inverse transform of both sides.
We will get y as a function of t. which is the required solution.
Example-1: Use Laplace transform method to solve the following equation-
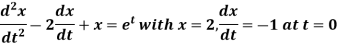
Sol. Here we have-
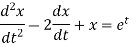
Take Laplace transform of both sides, we get-
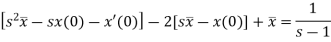
It becomes-
(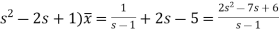
So that-
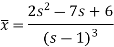
Now breaking it into partial fractions-
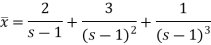
We get the following results on inversion-
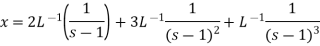
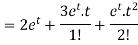
Example-2: Use Laplace transform method to solve the following equation-
|
Sol.
Here, taking the Laplace transform of both sides, we get
|
It becomes-
|
On inversion, we get-
|
Example-3: Use Laplace transform method to solve the following equation-
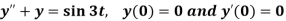
Sol. Here we have-
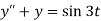
Taking Laplace transform of both sides, we get-
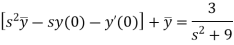
We get on putting given values-

On inversion, we get-


Example-4: Find the solution of the initial value problem by using Laplace transform-
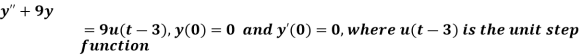
Sol. Here we have-
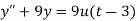
Taking Laplace transform, we get-
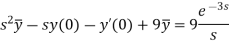
Putting the given values, we get-
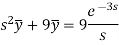
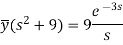
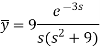
On inversion, we get-

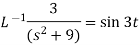
|
Now-
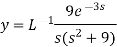
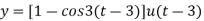
The Fourier integral of f(x) is-
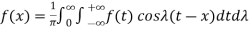 ………. (1)
………. (1)
Which can be written as-
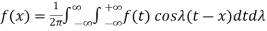 …………… (2)
…………… (2)
Because 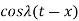 is an even function of
is an even function of 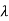 . Also since
. Also since 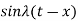 is an odd function of
is an odd function of 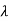 then we have-
then we have-
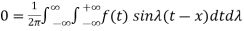 ……… (3)
……… (3)
Multiply (3) by ‘i’ and add to (2)-
We get-
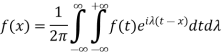
Which is the complex form of the Fourier integral.
Example 1:
Using complex form,find the Fourier series of the function
f(x) = sinx = 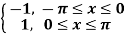
Solution:
We calculate the coefficients 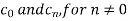
|
=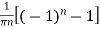
Hence the Fourier series of the function in complex form is
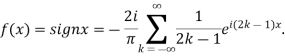
We can transform the series and write it in the real form by renaming as
n=2k-1,n=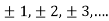
|
|
= 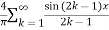
Example 2:
Using complex form find the Fourier series of the function f(x) = x2, defined on te interval [-1,1]
Solution:
Here the half-period is L=1.Therefore, the co-efficient c0 is,
|
For n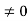
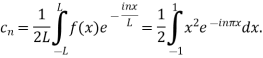
Integrating by parts twice,we obtain
=
=
=
=
|
Fourier integral theorem-
Fourier integral theorem can be stated as-
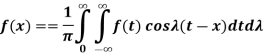
Proof: we have the Fourier series of a function f(x) in interval (-c, c) is-
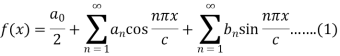
And  are given as-
are given as-
|
Put the values of  in equation (1), we get-
in equation (1), we get-
|
As we know that cosine functions are even functions, then-
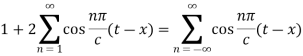
Equation (2) reduces to-
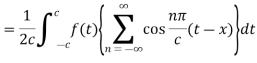
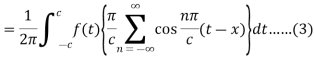
Here we will assume that c increases indefinitely, therefore we can take,
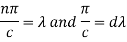
By this assumption, we get-
|
From equation (3) and (4), we get-
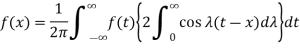
So that-
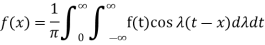
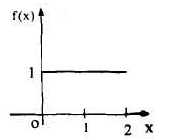
Example:1
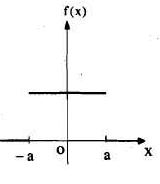
Find the fourier integral representation of the function
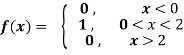
Solution:
The graph of the function is shown in the below figure satisfies the hypothesis of
Theorem -1 . Hence from Eqn,(5) and (6), we have
|

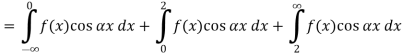
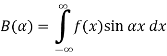

Substituting these coefficients in Eqn.(4) we obtain
|
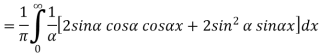
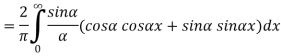
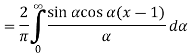
This is the Fourier integral representation of the given function.
Example:2
Find the Fourier integral representation of the function
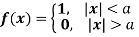
Solution:
The graph of the given function is shown in the below figure . Clearly, the given function f(x) is an even function. We represent f(x) by the fourier cosine integral . We obtain
|
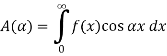
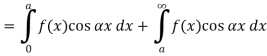

And thus ,
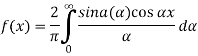
Key takeaways-
- The Fourier integral of f(x) is-
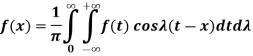
2. Complex form of the Fourier integral-

3. Fourier integral theorem-

In mathematics, a Fourier transform (FT) is a mathematical transform that decomposes a function (often a function of time, or a signal) into its constituent frequencies, such as the expression of a musical chord in terms of the volumes and frequencies of its constituent notes. The term Fourier transform refers to both the frequency domain representation and the mathematical operation that associates the frequency domain representation to a function of time.
The Fourier transform of a function of time is a complex-valued function of frequency, whose magnitude (absolute value) represents the amount of that frequency present in the original function, and whose argument is the phase offset of the basic sinusoid in that frequency. The Fourier transform is not limited to functions of time, but the domain of the original function is commonly referred to as the time domain. There is also an inverse Fourier transform that mathematically synthesizes the original function from its frequency domain representation, as proven by the Fourier inversion theorem
The function-
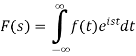
Is called the Fourier transform of the function f(x).
The function f(x) given below is called inverse Fourier transform of F(s)-
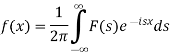
Properties of Fourier transform-
Property-1: Linear property- If F(s) and G(s) are two Fourier transforms of f(x) and g(x) respectively, then-
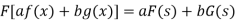
Where a and b are the constants.
Property-2: Change of scale- If F(s) is a Fourier transform of f(x), then
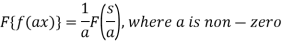
Property-3: Shifting property- If F(s) is a Fourier transform of f(x), then
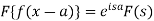
Property-4: Modulation- If F(s) is a Fourier transform of f(x), then
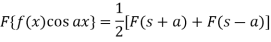
Example: Find the Fourier transform of-
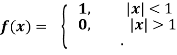
Hence evaluate 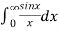
Sol. As we know that the Fourier transform of f(x) will be-
|
So that-
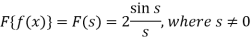
For s = 0, we get- F(s) = 2
Hence by the inverse formula, we get-
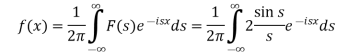
Putting x = 0, we get
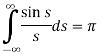
So-
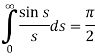
Example: Find the Fourier transform of 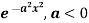
Sol. As we know that the Fourier transform of f(x) will be-
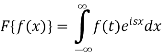
So that-
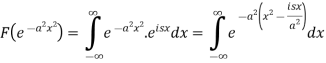
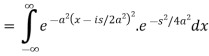
Now put 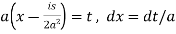

So that-
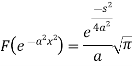
Key takeaways-
- The function-

Is called the Fourier transform of the function f(x).
2. Linear property- If F(s) and G(s) are two Fourier transforms of f(x) and g(x) respectively, then-
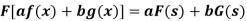
3. Change of scale- If F(s) is a Fourier transform of f(x), then
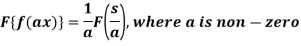
4. Shifting property- If F(s) is a Fourier transform of f(x), then

5. Modulation- If F(s) is a Fourier transform of f(x), then
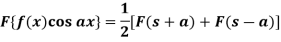
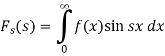
Then-

The function 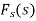 is known as the Fourier sine transform of f(x) in 0<x<∞
is known as the Fourier sine transform of f(x) in 0<x<∞
And the function f(x) s called the inverse Fourier sine transform of  .
.
And-
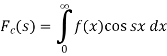
Then
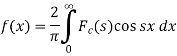
The function 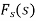 is known as the Fourier cosine transform of f(x) in 0<x<∞
is known as the Fourier cosine transform of f(x) in 0<x<∞
And the function f(x) s called the inverse Fourier cosine transform of 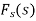 .
.
Finite Fourier sine and cosine transforms-
The finite Fourier sine transform of f(x), in 0<x<c, is given by-
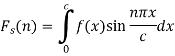
Where n is an integer.
And the function f(x) is called the inverse finite Fourier sine transform of 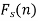 which is defined by-
which is defined by-
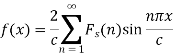
The finite Fourier cosine transform of f(x), in 0<x<c, is given by-
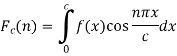
Where n is an integer.
And the function f(x) is called the inverse finite Fourier cosine transform of  which is defined by-
which is defined by-
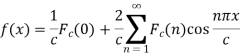
Inverse Fourier transforms
The f(x) given below is called inverse Fourier transform of F(s)-
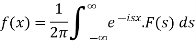
- Inverse Fourier sine transform of F(s)-

2. Inverse Fourier cosine transform of F(s)-
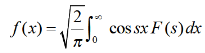
Example-1: Find the Fourier sine transform of 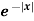
Sol. Here x being positive in the interval (0, ∞)
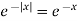
Fourier sine transform of 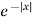 will be-
will be-
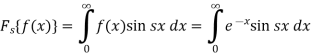
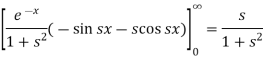
Example-2: Find the Fourier cosine transform of-
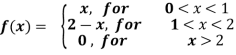
Sol. We know that the Fourier cosine transform of f(x)-
= = =
|
Example-3: Find the Fourier sine transform of 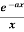
Sol. Let 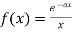
Then the Fourier sine transform will be-

Now suppose,
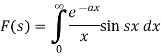
Differentiate both sides with respect to x, we get-
|
On integrating (1), we get-
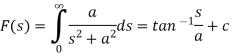
Key takeaways-

Where n is an integer.
2. The finite Fourier cosine transform of f(x), in 0<x<c, is given by-
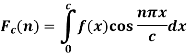
Where n is an integer.
3. Inverse Fourier sine transform of F(s)-
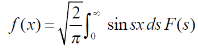
4. Inverse Fourier cosine transform of F(s)-
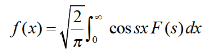
References
1. Erwin Kreyszig, Advanced Engineering Mathematics, 9thEdition, John Wiley & Sons, 2006.
2.N.P. Bali and Manish Goyal, A textbook of Engineering Mathematics, Laxmi Publications.
3. Higher engineering mathematic, Dr. B.S. Grewal, Khanna publishers