Unit - 3

Numerical Integration

3.1 Numerical Integration (1D): Trapezoidal rule

Numerical integration is a process of evaluating or obtaining a definite integral from a set of numerical values of the integrand f(x).In case of function of single variable, the process is called quadrature.

Trapezoidal rule

Let the interval 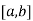be divided into n equal intervals such that 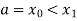<<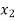…. <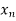=b.

Here.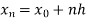

To find the value of.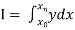

Setting n=1, we get

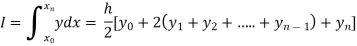
Or I =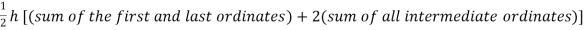

The above is known as Trapezoidal method.

Note: In this method second and higher difference are neglected and so f(x) is a polynomial of degree 1.

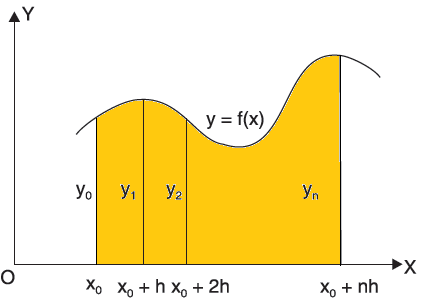
Geometrical Significance: The curve y=f(x), is replaced by n straight lines with the points (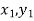);()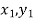 and (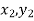)……. ;(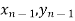) and ().

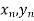The area bounded by the curve y=f(x), the ordinates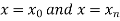,and the x axis is approximately equivalent to the sum of the area of the n trapeziums obtained.

Example1: State the trapezoidal rule for finding an approximate area under the given curve. A curve is given by the points (x, y) given below:

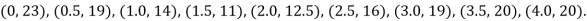
Estimate the area bounded by the curve, the x axis and the extreme ordinates.

We construct the data table:

Here length of interval h =0.5, initial value a = 0 and final value b = 4

By Trapezoidal method

Area of curve bounded on x axis =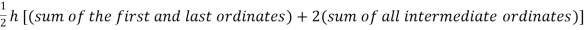

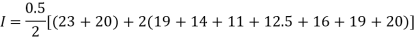
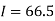
Example2: Compute the value of   ?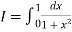

Using the trapezoidal rule with h=0.5, 0.25 and 0.125.

Here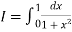

For h=0.5, we construct the data table:

By Trapezoidal rule

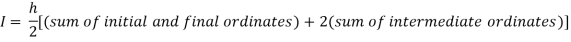
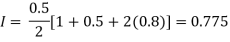
For h=0.25, we construct the data table:

By Trapezoidal rule

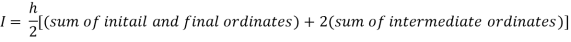
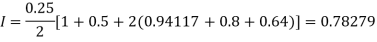
For h = 0.125, we construct the data table:

By Trapezoidal rule

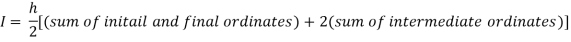
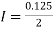[(1+0.5) +2(0.98461+0.94117+0.87671+0.8+0.71910+0.64+0.56637)]

Example3: Evaluate, using trapezoidal rule with five ordinates

Here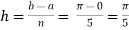

We construct the data table:

X	0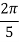
Y	0	0.3693161	1.195328	1.7926992	1.477265	0

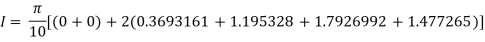
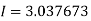
Key takeaways

1. Numerical integration is a process of evaluating or obtaining a definite integral 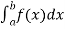from a set of numerical values of the integrand f(x).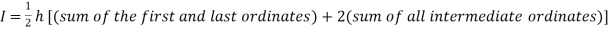
2. 

3.2 Simpson’s 1/3rd Rule

Overview-

Generally fundamental theorem of calculus is used find the solution for definite integrals, but sometime integration becomes too hard to evaluate, numerical methods are used to find the approximated value of the integral.

Simpson’s rules are very useful in numerical integration to evaluate such integrals.

Here we will understand the concept of Simpson’s rule and evaluate integrals by using numerical technique of integration.

We find more accurate value of the integration by using Simpson’s rule than other methods

Simpson’s rule

We will study about Simpson’s one-third rule and Simpson’s three-eight rules.

But in order to get these two formulas, we should have to know about the general quadrature formula-

General quadrature formula-

The general quadrature formula is gives as-

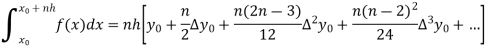
Simpson’s one-third and three-eighth formulas are derived by putting n = 2 and n = 3 respectively in general quadrature formula.

Simpson’s one-third and three-eighth formulas are derived by putting n = 2 and n = 3 respectively in general quadrature formula.

Let the interval 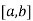be divided into n equal intervals such that 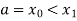<<…. <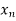=b.

Here.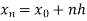

To find the value of.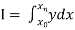

Setting n = 2,

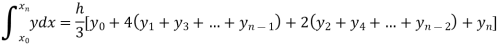
Which is known as Simpson’s 1/3- rule or Simpson’s rule.

Note: In this rule third and higher differences are neglected a so f(x) is a polynomial of degree 2.

Example: Estimate the value of the integral

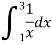
By Simpson’s rule with 4 strips and 8 strips respectively.

For n=4, we have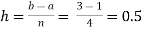

Construct the data table:

By Simpson’s Rule

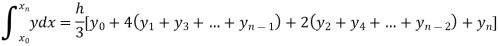
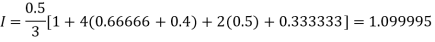
For n = 8, we have

By Simpson’s Rule

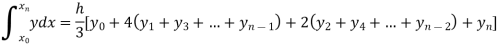
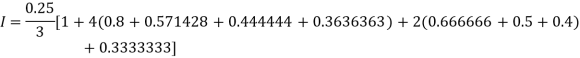
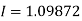
Example: Evaluate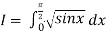

Using Simpson’s 1/3 rule with .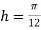

For 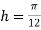, we construct the data table:

X	0
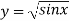	0	0.50874	0.707106	0.840896	0.930604	0.98281	1

By Simpson’s Rule

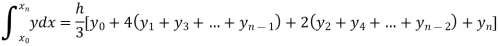
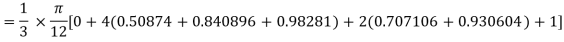
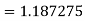
Example: Using Simpson’s 1/3 rule with h = 1, evaluate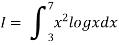
 

For h = 1, we construct the data table:

X	3	4	5	6	7
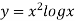	9.88751	22.108709	40.23594	64.503340	95.34959

By Simpson’s Rule
 

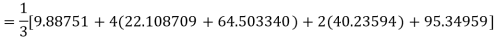
= 177.3853

Example: Evaluate the following integral by using Simpson’s 1/3rd rule.

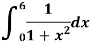
Solution-

First, we will divide the interval into six parts, where width (h) = 1, the value of f(x) is given in the table below-

x	0	1	2	3	4	5	6
f(x)	1	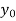0.5	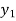0.2	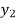0.1	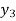1/17 = 0.05884	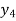1/26 = 0.0385	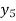1/37 = 0.027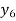

Now using Simpson’s 1/3rd rule-

We get-

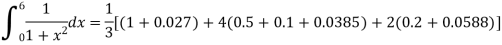
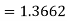
Example: Find the approximated value of the following integral by using Simpson’1/3rd rule.

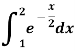
Solution-

The table of the values-

x	1	1.25	1.5	1.75	2
f(x)	0.60653	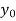0.53526	0.47237	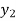0.41686	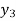0.36788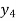

Now using Simpson’s 1/3rd rule-

We get-

Example2: Evaluate 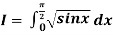Using Simpson’s 1/3 rule with .

For 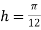, we construct the data table:

X	0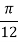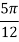
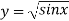	0	0.50874	0.707106	0.840896	0.930604	0.98281	1

By Simpson’s Rule

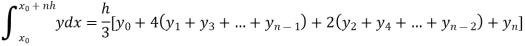
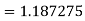
Example3: Using Simpson’s 1/3 rule with h = 1, evaluate

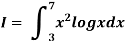
For h = 1, we construct the data table:

X	3	4	5	6	7
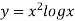	9.88751	22.108709	40.23594	64.503340	95.34959

By Simpson’s Rule

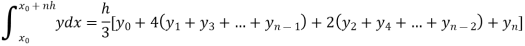
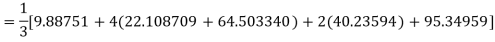
= 177.3853

3.3 Simpson’s 3/8 rule

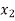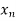Let the interval be divided into n equal intervals such that <<…. <=b.

Here.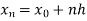

To find the value of .

Setting n=3, we get

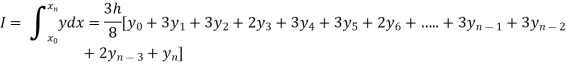
Is known as Simpson’s 3/8 rule which is not as accurate as Simpson’s rule.

Note: In this rule the fourth and higher differences are neglected and so f(x) is a polynomial of degree 3.

Example1: Evaluate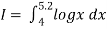

By Simpson’s 3/8 rule.

Let us divide the range of the interval [4, 5.2] into six equal parts.

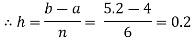
For h=0.2, we construct the data table:

X	4.0	4.2	4.4	4.6	4.8	5.0	5.2
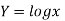	1.3863	1.4351	1.4816	1.5261	1.5686	1.6094	1.6487

By Simpson’s 3/8 rule

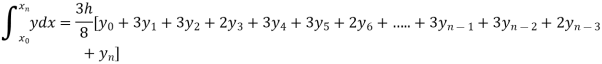
= 1.8278475

Example2: Evaluate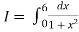

Let us divide the range of the interval [0,6] into six equal parts.

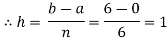
For h=1, we construct the data table:

X	0	1	2	3	4	5	6
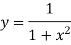	1	0.5	0.2	0.1	0.0588	0.0385	0.027

By Simpson’s 3/8 rule

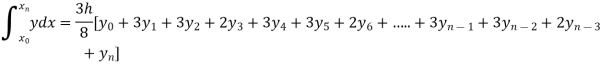
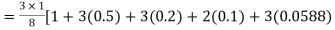+3(0.0385) +0.027]

=1.3571

Error in Trapezoidal method

The total error in trapezoidal method is given by

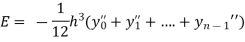
Let 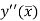is the largest value of the n quantities on the right hand side of the above equation then

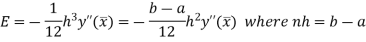
Error in Simpson’s Rule

The error in the Simpson’s rule is given by

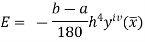
Where 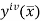is the largest value of the fourth derivative of y(x).

Error in Simpson’s 3/8 Rule

The error in this rule is given by

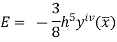
Where 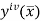is the largest value of the derivative of y(x).

Key takeaways

1. The general quadrature formula is gives as-

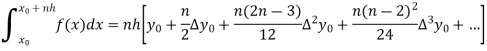
2.     Simpson’s one-third rule-

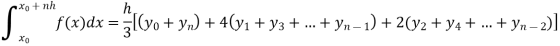
3.     Simpson’s three-eighth rule-

3.4 Gauss Quadrature 2-point and 3-point method

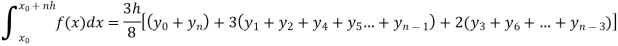
Quadrature: It is the process to evaluate the value of the functions at the chosen point, to its exact value for polynomial up to higher degree as possible.

The general form Gaussian quadrature is given by

Where 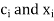depends on the choice of n (number of points).

Also note that the possible polynomial of degree up to .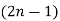

. …... (1)

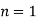For point

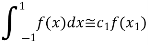
Which gives exact value of the polynomial up to degree 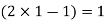degree

i.e.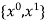

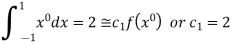
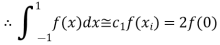
For 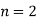point and using (1)

Which gives exact value of the polynomial up to degree 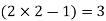degree

i.e.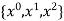

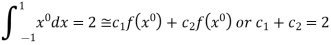
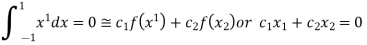
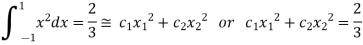
On solving we get

.

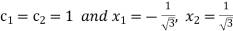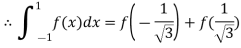
Gauss Quadrature 3-point method:

The general form Gaussian quadrature is given by

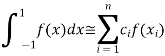
Where depends on the choice of n (number of points).

Also note that the possible polynomial of degree up to .

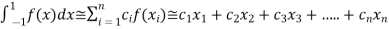. …... (1)

For point

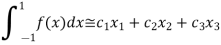
Which gives exact value of the polynomial up to degree 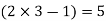degree

i.e.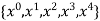

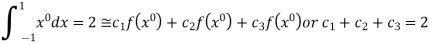
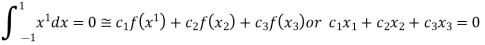
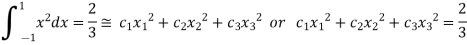
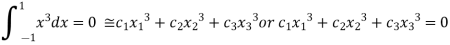
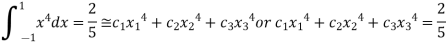
On solving we get

.

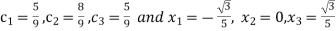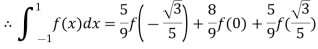
For n=3,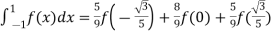

Note:  To evaluate 

The above integral can be converted into Gauss quadrature by substituting

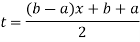
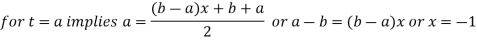
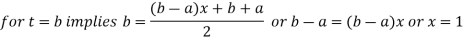
Hence  .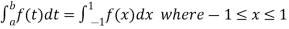

Example: Evaluate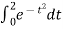

Here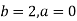

Using =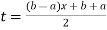

Also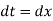

For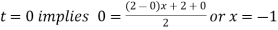

For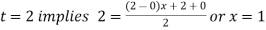

Hence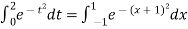

Here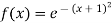

By Gauss quadrature 3 point rule

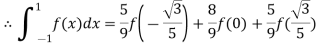
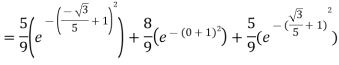
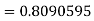
Example: Evaluate 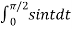 by 2-point Gaussian rule.

Here

Using =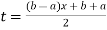

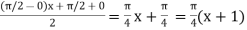
Also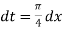

For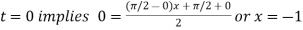

For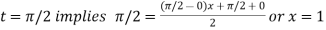

Hence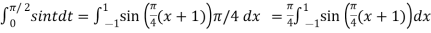

Here

By Gauss quadrature 2 point rule

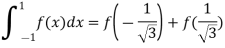
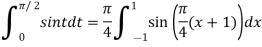
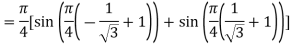
=0.99847

Example: Solve by Gauss quadrature 3-point method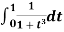

Given

Here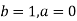

Using =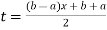

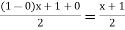
Also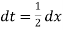

For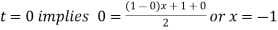

For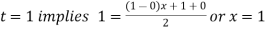

Hence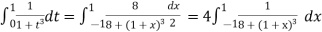

Here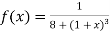

By Gauss quadrature 3 point rule

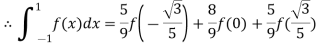
Hence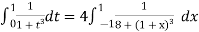

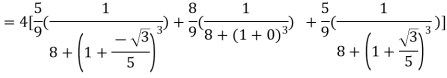
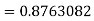
3.5 Double Integration: Trapezoidal rule

The double integration is defined by

Where.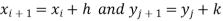

Trapezoidal Rule:

The double integration is defined by

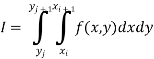
Where.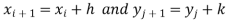

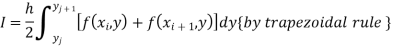
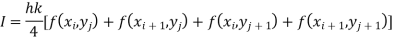
Or    

Also, the double integration is defined by

Where.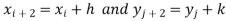

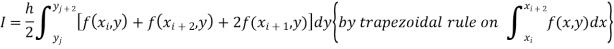
Again, Applying Trapezoidal rule to each term with respect to y.

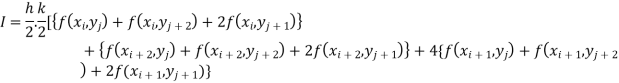
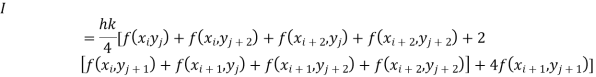
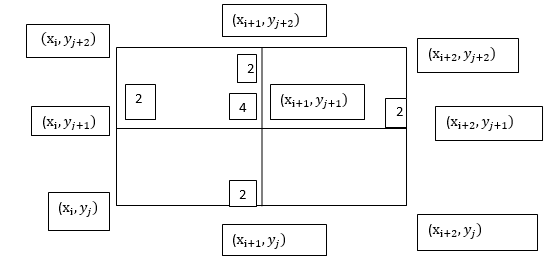
To remember we can use

Example1: Evaluate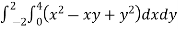

Let

Here the interval of x and y are 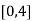and .

Let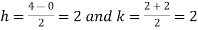 

Consider the following table:

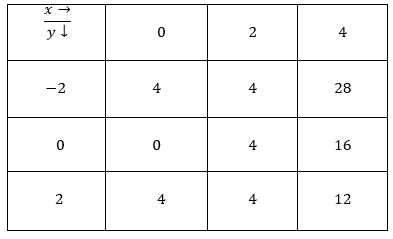
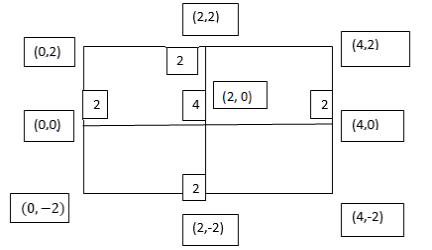
By Trapezoidal Rule

.

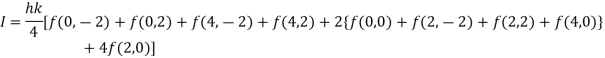
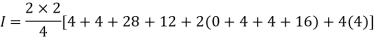
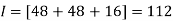Example2: Evaluate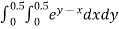 

Let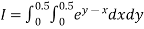

Here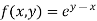

Let the number of intervals be .

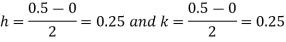
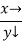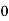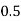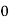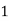
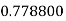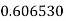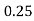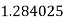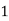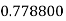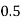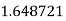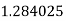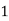By Trapezoidal Rule

.

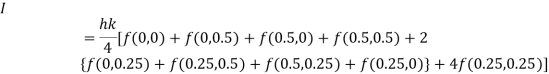
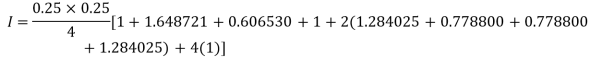
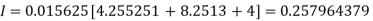Example3: Evaluate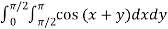

Let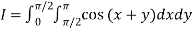 

And

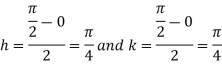
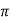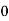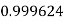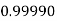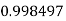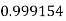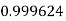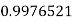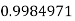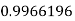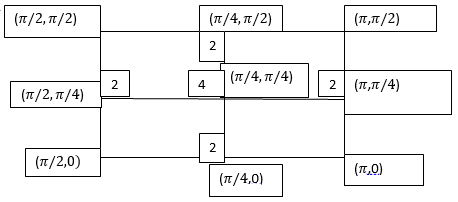
By Trapezoidal Rule

3.6 Simpson’s 1/3rd rule:

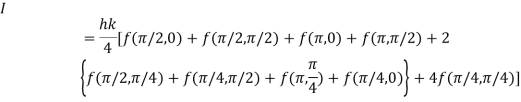
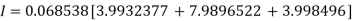
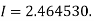
The double integration is defined by

By Simpson’s 1/3 rd Rule

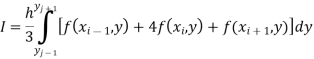
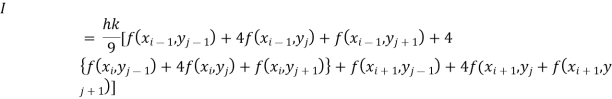
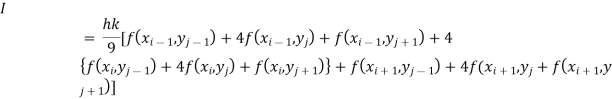
Also, the double integration is defined by

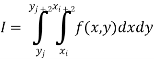
Where.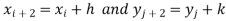

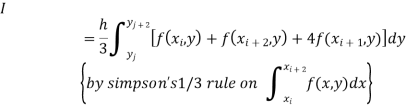
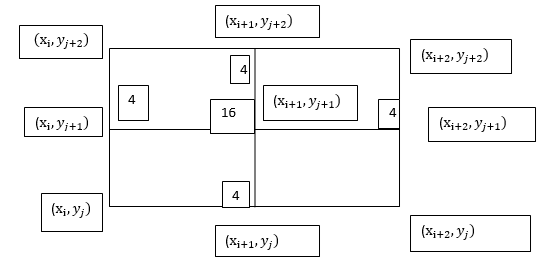
Again, Applying Simpson’s 1/3 rd rule to each term with respect to y.

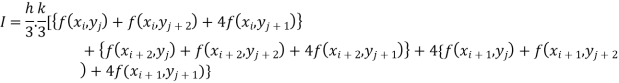
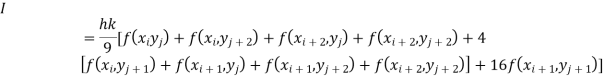
To remember we can use

Example1: Evaluate 

Let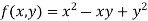

Here the interval of x and y are 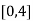and .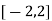

Let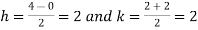 

Consider the following table:

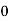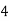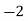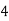
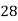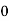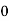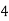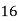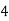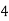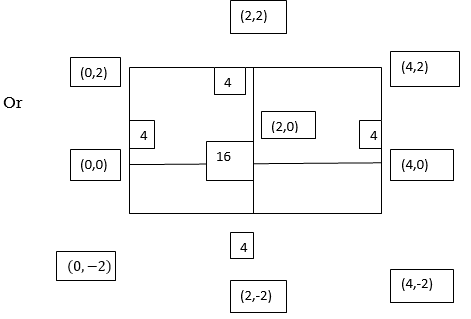
By Simpson’s 1/3 Rule

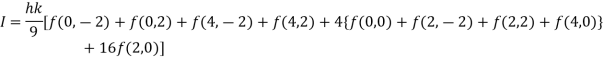
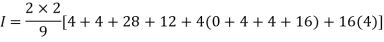
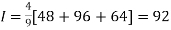.4444444

Example2: Evaluate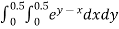 

Let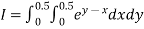

Here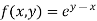

Let the number of intervals be .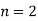

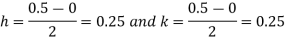
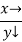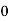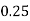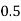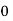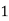
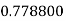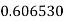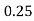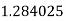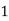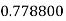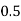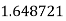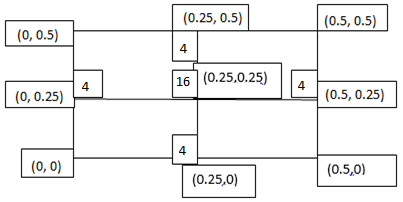
By Simpson’s 1/3 Rule

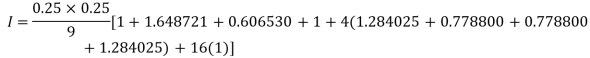
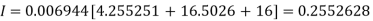
Example3: Evaluate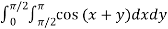

Let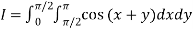 

And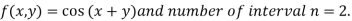

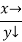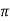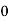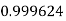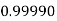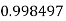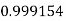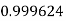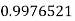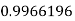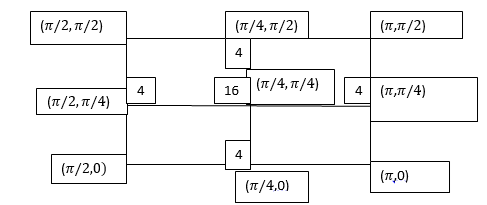
By Simpson’s 1/3 Rule

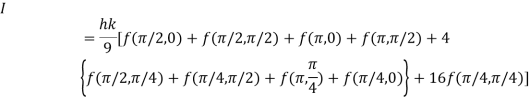
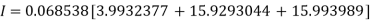
References:

1. E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
2. P. G. Hoel, S. C. Port and C. J. Stone, “Introduction to Probability Theory”, Universal Book Stall, 2003.
3. S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
4. W. Feller, “An Introduction to Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
5. N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
6. B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
7. T. Veerarajan, “Engineering Mathematics”, Tata Mcgraw-Hill, New Delhi, 2010
8. Higher engineering mathematics, HK Dass
9. Higher engineering mathematics, BV Ramana.
10. Computer based numerical & statistical techniques, M goyal