Unit - 4
Curve Fitting and Regression Analysis
Suppose we are fitting the nth degree curve

To the given values  of two variables x and y.
of two variables x and y.
For that we need to find a, b, c,….,k i.e. (n+1) constant that would fits best in the above curve of given degree.
Case1: if m=n+1, we get (n+1) equation by substituting the unknowns we get a unique solution
Case 2: if m>n+1 then no unique solution is possible. For such cases the method of least square is used.
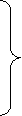 Let us suppose we get
Let us suppose we get 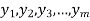 values corresponding to
values corresponding to 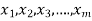 respectively. So that,
respectively. So that,
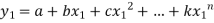
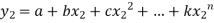
………………………………. (2)
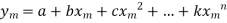
A curve which has the properties of best fitting curve in the sense of least square of given data, is called a least square curve.
Let 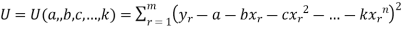
The necessary condition for U to be maximum or minimum are given by
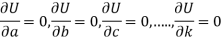
It reduces
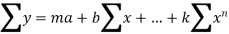
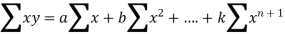
………………………………………
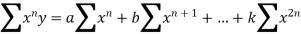
By solving this simultaneous (n+1) equations we get the values of a, b, c,…,k.
The Second order partial derivative of U is to be calculated and on substitution of a, b, c,…,k we get the minimum value of U.
Particular:
I) When n=1 or fitting on a straight line:
Let the equation be 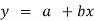
And its normal equation is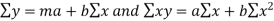
II) When n=2 or fitting of second degree parabola:
The equation of curve is 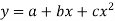
The normal equations are
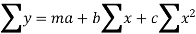
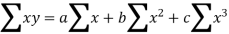

The values of 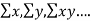 etc are calculated by means of table (S.D.) and then the value a, b, c…. Are determined.
etc are calculated by means of table (S.D.) and then the value a, b, c…. Are determined.
Example: Fit a straight line to the following data regarding x as the independent variables:
X | 0 | 1 | 2 | 3 | 4 |
Y | 1 | 1.8 | 3.3 | 4.5 | 6.3 |
The equation of straight line is
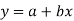
And the normal equations
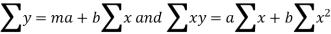
We construct the data table:
X | Y | XY | 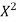 |
0 1 2 3 4 | 1 1.8 3.3 4.5 6.3 | 0 1.8 6.6 13.5 25.2 | 0 1 4 9 16 |
Total  | 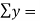 | 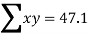 |  |
Here 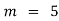 (no. Of steps)
(no. Of steps)
Substituting the values from table in normal equations:
16.9=5a+10b
47.1=10a+30b
On solving we get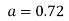 and
and 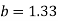
Therefore, the required equation of the straight line is 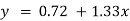 .
.
Example: Find the straight line that best fits of the following data by using method of least square.
X | 1 | 2 | 3 | 4 | 5 |
y | 14 | 27 | 40 | 55 | 68 |
Sol.
Suppose the straight line
y = a + bx…….. (1)
Fits the best-
Then-
x | y | Xy |  |
1 | 14 | 14 | 1 |
2 | 27 | 54 | 4 |
3 | 40 | 120 | 9 |
4 | 55 | 220 | 16 |
5 | 68 | 340 | 25 |
Sum = 15 | 204 | 748 | 55 |
Normal equations are-
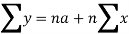

Put the values from the table, we get two normal equations-
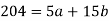
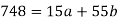
On solving the above equations, we get-
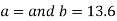
So that the best fit line will be- (on putting the values of a and b in equation (1))
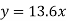
Example2: Fit a second-degree parabola to the following data regarding x as an independent variable:
X | 0 | 1 | 2 | 3 | 4 |
Y | 1 | 5 | 10 | 22 | 38 |
The equation of second-degree curve is

The normal equations are
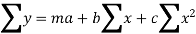
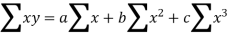
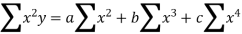
We construct the data table:
X | Y | 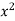 | 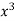 | 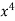 | 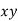 | 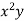 |
0 1 2 3 4 | 1 5 10 22 38 | 0 1 4 9 16 | 0 1 8 27 64 | 0 1 16 81 256 | 0 5 20 66 152 | 0 5 40 198 608 |
Total 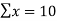 |  | 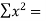 | 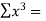 | 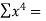 | 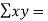 |  |
Substituting these values from the table in the above equations
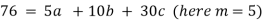


On solving we get 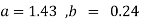 and
and 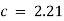
Therefore equation of parabola is 
Example: Find the best values of a and b so that y = a + bx fits the data given in the table
x | 0 | 1 | 2 | 3 | 4 |
y | 1.0 | 2.9 | 4.8 | 6.7 | 8.6 |
Solution.
y = a + bx
x | y | Xy | 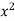 |
0 | 1.0 | 0 | 0 |
1 | 2.9 | 2.0 | 1 |
2 | 4.8 | 9.6 | 4 |
3 | 6.7 | 20.1 | 9 |
4 | 8.6 | 13.4 | 16 |
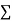 | 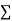 | 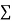 | 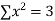 |
Normal equations, 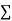 y= na+ b
y= na+ b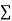 x (2)
x (2)
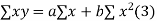
On putting the values of 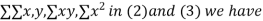
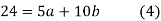
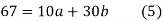
On solving (4) and (5) we get,
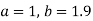
On substituting the values of a and b in (1) we get
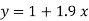
Example3: Predict y at x = 3.75 by fitting a power curve 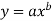 to the given data
to the given data
X | 1 | 2 | 3 | 4 | 5 | 6 |
Y | 2.98 | 4.26 | 5.21 | 6.10 | 6.80 | 7.50 |
Given equation is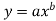
Taking log on both sides,

Let 
Therefore, its normal equation is
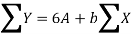

We construct the data table:
 |  | 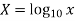 | 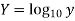 | XY | 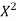 |
1 2 3 4 5 6 | 2.98 4.26 5.21 6.10 6.80 7.50 | 0 0.301030 0.477121 0.602060 0.698970 0.778151 | 0.474216 0.629410 0.716838 0.785330 0.832509 0.875061 | 0 0.189471 0.342018 0.472816 0.581899 0.680930 | 0 0.090619 0.227644 0.362476 0.488559 0.605519 |
Total
|
| 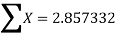 | 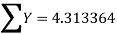 |  | 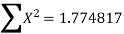 |
Substituting the values from the table in the above equations
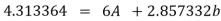
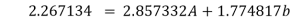
On solving we get 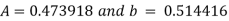
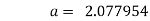
Hence the required equation is 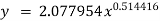
So, 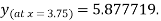
Example4: Use the least square method to determine a and b in the formula
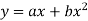
For the following observations
X | 1 | 2 | 3 | 4 | 5 |
Y | 1.8 | 5.1 | 8.9 | 14.1 | 19.8 |
The given equation by
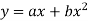
Therefore its rational equation is

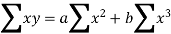
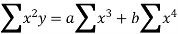
We construct the data table:
X | Y |  | 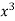 | 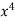 | 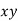 | 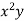 |
1 2 3 4 5
| 1.8 5.1 8.9 14.1 19.8 | 1 4 9 16 25 | 1 8 27 64 125 | 1 16 81 264 625 | 1.8 10.2 26.7 56.4 99.0 | 1.8 20.4 80.1 225.6 495 |
Total 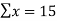 | 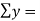 | 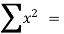 55 | 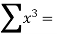 225
| 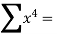 987
| 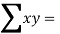 194.1
| 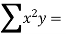 822.9 |
Substituting the above values from the table to the above equations
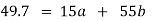
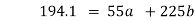
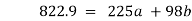
On solving we get 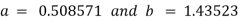
Hence the required equation is 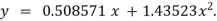
Example: Fit a second degree parabola to the following data by least squares method.
 | 1929 | 1930 | 1931 | 1932 | 1933 | 1934 | 1935 | 1936 | 1937 |
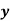 | 352 | 356 | 357 | 358 | 360 | 361 | 361 | 360 | 359 |
Solution: Taking 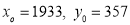
Taking 

The equation 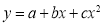 is transformed to
is transformed to 
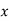 | 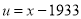 | 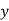 |  | 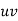 | 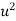 |  | 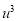 | 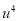 |
1929 | -4 | 352 | -5 | 20 | 16 | -80 | -64 | 256 |
1930 | -3 | 360 | -1 | 3 | 9 | -9 | -27 | 81 |
1931 | -2 | 357 | 0 | 0 | 4 | 0 | -8 | 16 |
1932 | -1 | 358 | 1 | -1 | 1 | 1 | -1 | 1 |
1933 | 0 | 360 | 3 | 0 | 0 | 0 | 0 | 0 |
1934 | 1 | 361 | 4 | 4 | 1 | 4 | 1 | 1 |
1935 | 2 | 361 | 4 | 8 | 4 | 16 | 8 | 16 |
1936 | 3 | 360 | 3 | 9 | 9 | 27 | 27 | 81 |
1937 | 4 | 359 | 2 | 8 | 16 | 32 | 64 | 256 |
Total | 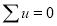 |
| 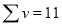 |  | 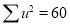 | 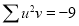 | 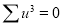 | 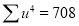 |
Normal equations are
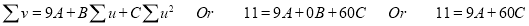
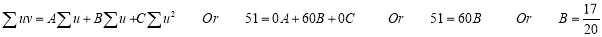
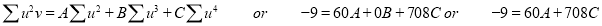
On solving these equations, we get 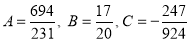
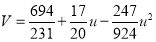

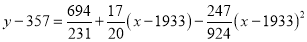
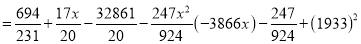
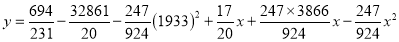
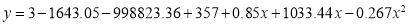
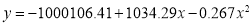
Example: Find the least squares approximation of second degree for the discrete data
x | 2 | -1 | 0 | 1 | 2 |
y | 15 | 1 | 1 | 3 | 19 |
Solution. Let the equation of second degree polynomial be 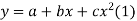
x | y | Xy | 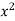 | 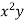 | 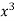 | 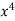 |
-2 | 15 | -30 | 4 | 60 | -8 | 16 |
-1 | 1 | -1 | 1 | 1 | -1 | 1 |
0 | 1 | 0 | 0 | 0 | 0 | 0 |
1 | 3 | 3 | 1 | 3 | 1 | 1 |
2 | 19 | 38 | 4 | 76 | 8 | 16 |
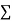 | 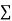 | 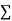 | 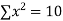 | 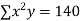 |  |  |
Normal equations are 
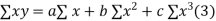
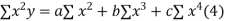
On putting the values of 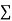 x,
x, 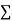 y,
y,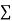 xy,
xy, 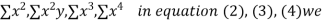 have
have
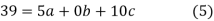
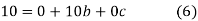
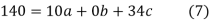
On solving (5), (6), (7), we get, 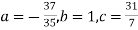
The required polynomial of second degree is
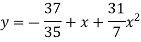
Example: Fit a second-degree parabola to the following data.
X = 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Y = 1.1 | 1.3 | 1.6 | 2.0 | 2.7 | 3.4 | 4.1 |
Solution
We shift the origin to (2.5, 0) antique 0.5 as the new unit. This amounts to changing the variable x to X, by the relation X = 2x – 5.
Let the parabola of fit be y = a + bX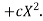 The values of
The values of 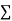 X etc. Are calculated as below:
X etc. Are calculated as below:
x | X | y | Xy | 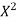 | 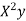 | 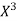 | 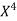 |
1.0 | -3 | 1.1 | -3.3 | 9 | 9.9 | -27 | 81 |
1.5 | -2 | 1.3 | -2.6 | 4 | 5.2 | -5 | 16 |
2.0 | -1 | 1.6 | -1.6 | 1 | 1.6 | -1 | 1 |
2.5 | 0 | 2.0 | 0.0 | 0 | 0.0 | 0 | 0 |
3.0 | 1 | 2.7 | 2.7 | 1 | 2.7 | 1 | 1 |
3.5 | 2 | 3.4 | 6.8 | 4 | 13.6 | 8 | 16 |
4.0 | 3 | 4.1 | 12.3 | 9 | 36.9 | 27 | 81 |
Total | 0 | 16.2 | 14.3 | 28 | 69.9 | 0 | 196 |
The normal equations are
7a + 28c =16.2; 28b =14.3; 28a +196c=69.9
Solving these as simultaneous equations we get
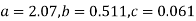

Replacing X bye 2x – 5 in the above equation we get
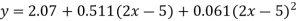
Which simplifies to y =
This is the required parabola of the best fit.
I. The simple linear regression is given by
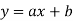
Where 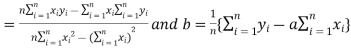 , n is number of given data.
, n is number of given data.
II. The multiple linear regression is
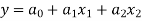
The normal equations are
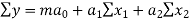 … (1)
… (1)
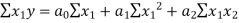 … (2)
… (2)
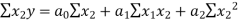 … (3)
… (3)
Example1: Create least square regression line of set of points
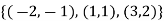
Here 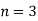 is number of data points.
is number of data points.
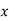 |
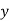 |
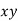 |
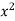 |
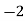 |
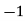 |
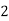 |
 |
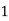 |
 |
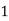 |
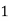 |
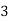 |
 |
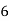 |
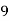 |
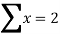 |
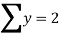 |
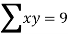 |
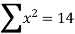 |
The simple linear regression is given by
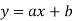
Where 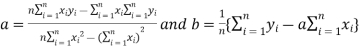
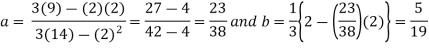
Here 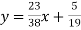 which is straight line.
which is straight line.
Example2: Find the linear square regression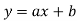 for the following data. Also find y when
for the following data. Also find y when 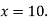
X | 0 | 1 | 2 | 3 | 4 |
Y | 1 | 3 | 5 | 4 | 6 |
Here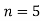 , number of data given.
, number of data given.
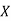 |
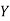 |
 |
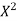 |
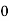 |
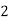 |
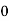 |
 |
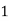 |
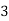 |
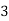 |
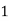 |
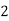 |
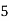 |
 |
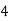 |
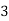 |
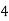 |
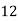 |
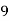 |
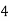 |
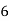 |
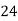 |
 |
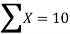 |
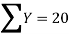 |
 |
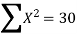 |
The simple linear regression is given by
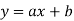
Where 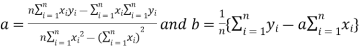
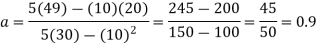
And 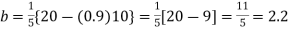
Hence the straight line is given by
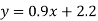
Also 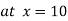

Example3: Fit the equation
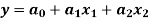
To the following data
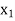 | 0 | 1 | 2 | 3 |
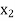 | 10 | 1 | 2 | 3 |
 | 12 | 18 | 24 | 30 |
The multiple linear regression is
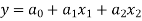
The normal equations are
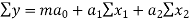 … (1)
… (1)
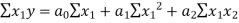 … (2)
… (2)
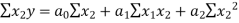 … (3)
… (3)
Consider the following table
|
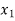 |
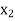 |
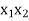 |
 |
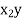 |
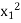 |
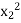 |
12 | 1 | 10 | 10 | 12 | 120 | 1 | 100 |
18 | 2 | 1 | 2 | 36 | 18 | 4 | 1 |
24 | 3 | 2 | 6 | 72 | 49 | 9 | 4 |
30 | 4 | 3 | 12 | 120 | 90 | 16 | 9 |
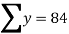 | 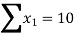 | 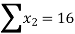 | 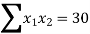 | 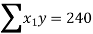 |
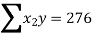 |
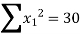 |
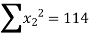 |
Substituting the values from the table in the above equations we get
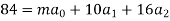
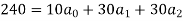
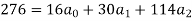
On solving we get 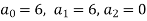
Hence the equation will be
 .
.
Or 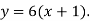
In multiple regression the number of variables is more than two (with one dependent variable and two or more independent variables).
We know that in agriculture, the crops does not depend on rainfall only but also fertilizers, pesticides, quality of seeds, soil etc.
Thus in multiple regression, the dependent variable Y is a function of more than one independent Variables.
Y= f (X1, X2, X3…, Xk)
Linear multiple regression
Let Y depends on two independent variables X1 and X2,
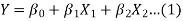
Then the linear multiple regression problem is to fit the regression plane given by Equation (1) to a
Given set of N triples.
To estimate the coefficient 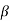 0,
0, 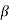 1,
1, 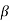 2, apply the least squares method to minimize
2, apply the least squares method to minimize
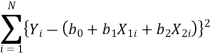
This results in three normal equations given by
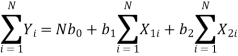
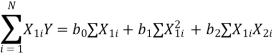
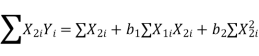
Here b0, b1, b2 are the least squares estimates of 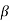 0,
0, 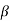 1,
1, 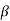 2
2
Example: Fit a regression plane to estimate 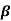 0,
0, 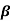 1,
1, 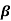 2 to the following data of a transport company on the weights of 6 shipments, the distances they were moved and the damage of the goods that was incurred. Estimate the damage when a shipment of 3700 kg is moved to a distance of 260 km.
2 to the following data of a transport company on the weights of 6 shipments, the distances they were moved and the damage of the goods that was incurred. Estimate the damage when a shipment of 3700 kg is moved to a distance of 260 km.
Weight(x1) in kg | 4 | 3 | 1.6 | 1.2 | 3.4 | 4.8 |
Distance(x2)km | 1.5 | 2.2. | 1.0 | 2.0 | 0.8 | 1.6 |
Damage(y)Rs, | 160 | 112 | 69 | 90 | 123 | 186 |
Sol.
Suppose the dependent variable damage be y, the two independent variables be weight x1 and distance x2. Thus assume the equation of the regression plane as
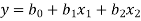
Where b0, b1, b2 are the estimates of β0, β1, β2.
The three normal equations are
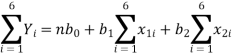
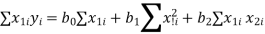
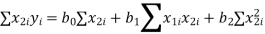
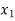 | 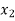 |  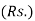 | 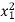 | 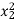 | 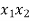 | 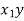 | 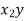 |
4.0 3.0 1.6 1.2 3.4 4.8 | 1.5 2.2 1.0 2.0 0.8 1.6 | 160 112 69 90 123 186 | 16 9 2.56 1.44 11.56 23.04 | 2.25 4.84 1.0 4.0 0.64 2.56 | 6.0 6.0 1.6 2.4 2.72 7.68 | 640 336 110.4 108 418.2 892.8 | 240 246.6 69 180 98.4 297.6 |
18 | 9.1 | 740 | 63.6 | 15.29 | 27 | 250.54 | 1131.4 |
The required regression plane we get
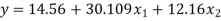
For a weight of 3700 kg (x1 = 3.7) and for a distance of 260 km (x2 = 2.6), the damage incurred in rupees is
y (x1 = 3.7, x2 = 2.6) = 14.56+30.109(3.7) +12.16(2.6)
= Rs. 714.5798 ≈ Rs. 715.
Let

Represent a polynomial in X of degree N.
For a given set of N pair of observations (Xi, Yi) the unknowns a0, a1, a2, . . ., aN are estimated by least square method by minimizing
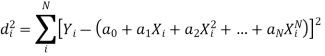
This results in the following (N + 1) normal equations for the determination of (N + 1) unknowns a0, a1, a2, . . ., aN.
Normal equations are
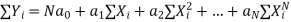

Let 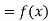 , be defined function we get
, be defined function we get
X | 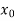 | 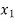 | 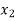 | ….. | 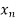 |
f(x) | 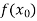 | 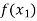 | 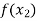 | …… | 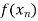 |
Where the interval is not necessarily equal. We assume f(x) is a polynomial of degree n. Then Lagrange’s interpolation formula is given by


Example1: Deduce Lagrange’s formula for interpolation. The observed values of a function are respectively 168,120,72 and 63 at the four position3,7,9 and 10 of the independent variables. What is the best estimate you can for the value of the function at the position of the independent variable?
We construct the table for the given data:
X | 3 | 6 | 7 | 9 | 10 |
Y=f(x) | 168 | ? | 120 | 72 | 63 |
We need to calculate for x = 6, we need f (6) =?
Here 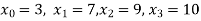
We get 
 By Lagrange’s interpolation formula, we have
By Lagrange’s interpolation formula, we have
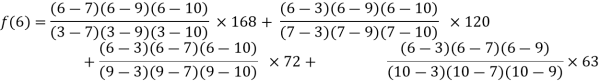
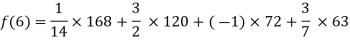
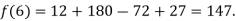
Hence the estimated value for x=6 is 147.
Example2: By means of Lagrange’s formula, prove that
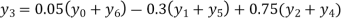
We construct the table:
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
Y=f(x) | 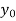 | 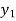 | 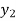 | 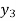 | 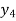 | 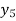 | 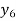 |
Here x = 3, f(x)=?
 By Lagrange’s formula for interpolation
By Lagrange’s formula for interpolation
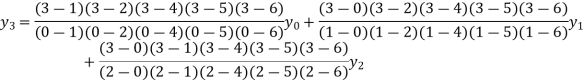
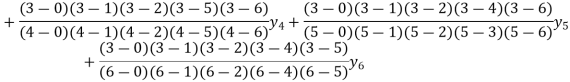
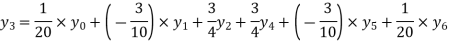
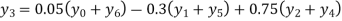
Hence proved.
Example3: find the polynomial of fifth degree from the following data
X | 0 | 1 | 3 | 5 | 6 | 9 |
Y=f(x) | -18 | 0 | 0 | -248 | 0 | 13104 |
Here 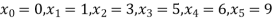
We get 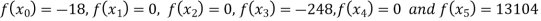
 By Lagrange’s interpolation formula
By Lagrange’s interpolation formula

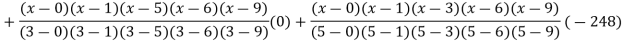
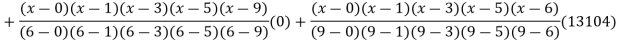

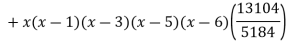
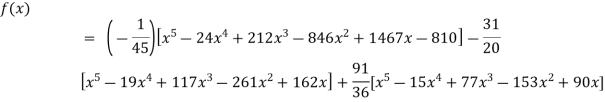
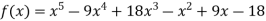
Interpolation
Definition: Interpolation is a technique of estimating the value of a function for any intermediate value of the independent variable while the process of computing the value of the function outside the given range is called extrapolation.
Let 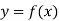 be a function of x.
be a function of x.
The table given below gives corresponding values of y for different values of x.
X | 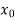 | 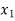 | 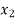 | …. | 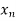 |
y= f(x) | 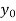 | 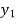 | 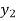 | …. |  |
The process of finding the values of y corresponding to any value of x which lies between 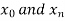 is called interpolation.
is called interpolation.
If the given function is a polynomial it is polynomial interpolation and given function is known as interpolating polynomial.
Conditions for Interpolation
1) The function must be a polynomial of independent variable.
2) The function should be either increasing or decreasing function.
3) The value of the function should be increase or decrease uniformly.
Finite Difference
Let 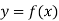 be a function of x. The table given below gives corresponding values of y for different values of x.
be a function of x. The table given below gives corresponding values of y for different values of x.
x | 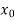 | 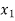 | 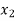 | …. | 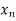 |
y= f(x) | 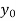 | 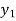 | 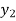 | …. | 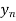 |
a) Forward Difference: Then 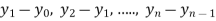 are called differences of y, denoted by
are called differences of y, denoted by 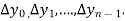
The symbol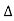 is called the forward difference operator. Consider the forward difference table below:
is called the forward difference operator. Consider the forward difference table below:




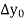

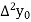

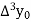

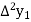
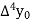
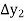
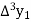


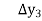


Where 
And 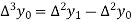 third forward difference so on.
third forward difference so on.
b) Backward Difference:
The difference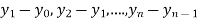 are called first backward difference and is denoted by
are called first backward difference and is denoted by  Consider the backward difference table below:
Consider the backward difference table below:

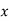 | 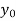 | | 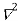 |  | 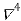 |

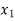
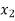
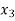
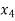 | 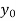
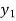
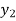
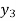
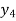 |
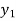
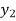

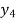 |
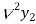

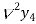 |
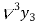
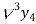 |
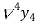 |
Where 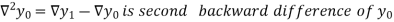
And 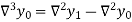 third backward differences so on.
third backward differences so on.
Newton Forward Difference formula:
This method is useful for interpolation near the beginning of a set of tabular values.
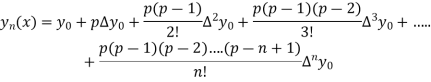
Where 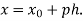
Example1: Using Newton’s forward difference formula, find the sum
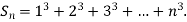
Putting 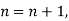
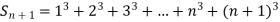
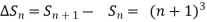
It follows that

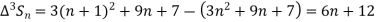
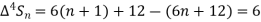
Since 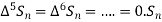 is a fourth-degree polynomial in n.
is a fourth-degree polynomial in n.
Further,
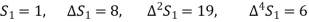
By Newton Forward Difference Method
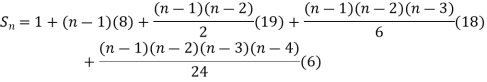
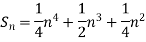
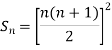
Example2: Given 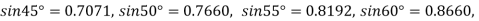 find
find  , by using Newton forward interpolation method.
, by using Newton forward interpolation method.
Let  , then
, then
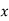 | 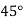 | 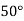 | 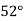 | 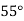 | 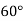 |
 | 0.7071 | 0.7660 | - | 0.8192 | 0.8660 |
The table of forward finite difference is given below:
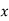 | 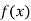 | 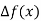 | 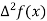 | 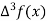 |
45
50
55
60 | 0.7071
0.7660
0.8192
0.8660 |
0.0589
0.0532
0.0468 |
-0.0057
-0.0064 |
-0.0007 |
By Newton forward difference method
Here initial value  = 45, difference of interval h = 5 and the value to be calculated at x=52.
= 45, difference of interval h = 5 and the value to be calculated at x=52.
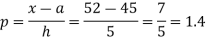
By Formula
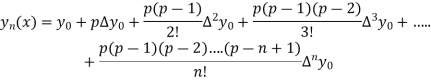
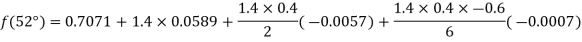
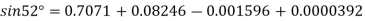

Example3: Find the missing term in the following:
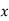 | 0 | 1 | 2 | 3 | 4 |
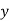 | 1 | 3 | 9 | ? | 81 |
Let 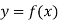
First we construct the forward difference table:
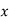 | 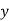 | 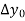 | 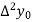 | 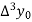 |
0
1
2
3
4 | 1
3
9
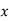
81 |
2
6
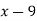
 |
4
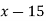
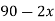 |
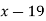
 |
Now, 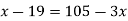
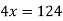
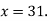
Newton Backward Difference Method:
This method is useful for interpolation near the ending of a set of tabular values.
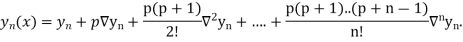
Where 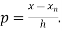
Example1: Find  from the following table:
from the following table:
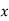 | 0.20 | 0.22 | 0.24 | 0.26 | 0.28 | 0.30 |
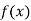 | 1.6596 | 1.6698 | 1.6804 | 1.6912 | 1.7024 | 1.7139 |
Consider the backward difference method
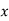 | 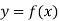 | 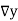 | 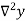 |  | 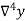 | 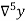 |
0.20
0.22
0.24
0.26
0.28
0.30 | 1.6596
1.6698
1.6804
1.6912
1.7024
1.7139 |
0.0102
0.0106
0.0108
0.0112
0.0115 |
0.0004
0.0002
0.0004
0.0003 |
-0.0002
0.0002
-0.0001 |
0.0004
-0.0003 |
-0.0007 |
Here 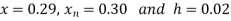
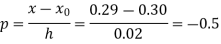
By Newton backward difference formula
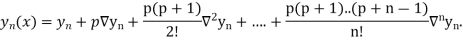
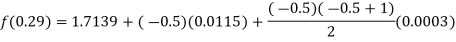
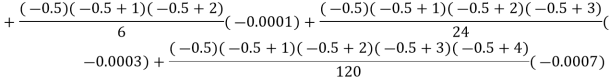
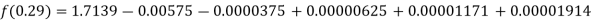

Example2: The following table give the amount of a chemical dissolved in water:
Temp. | 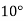 | 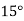 | 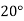 | 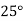 |  |  |
Solubility | 19.97 | 21.51 | 22.47 | 23.52 | 24.65 | 25.89 |
Compute the amount dissolve at 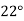
Consider the following backward difference table:
Temp. x | Solubility y |  |  |  | 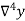 | 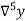 |
10
15
20
25
30
35 | 19.97
21.51
22.47
23.52
24.65
25.89 |
1.54
0.96
1.05
1.13
1.24 |
-0.58
0.09
0.08
0.11 |
0.67
-0.01
0.03 |
-0.68
0.04 |
0.72 |
Here 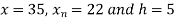
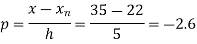
By Newton Backward difference formula
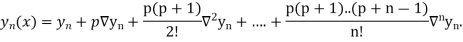

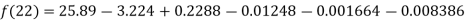
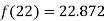
Example3: The following are the marks obtained by 492 candidates in a certain examination
Marks | 0-40 | 40-45 | 45-50 | 50-55 | 55-60 | 60-65 |
No. of candidates | 210 | 43 | 54 | 74 | 32 | 79 |
Find out the number of candidates:
a) Who secured more than 48 but not more than 50 marks?
b) Who secured less than 48 but not less than 45 marks?
Consider the forward difference table given below:
Marks upto x | No. Of candidates y |  |  |  | 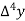 | 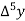 |
40
45
50
55
60
65 | 210
210+43=253
253+54=307
307+74=381
381+32=413
413+79= 492 |
43
54
74
32
79 |
11
20
-42
47 |
9
-62
89 |
-71
151 |
222 |
Here 

By Newton Forward Difference formula
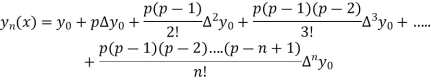
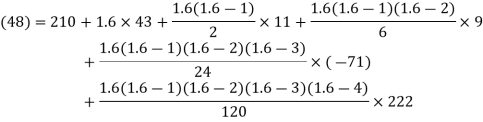
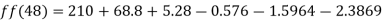
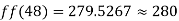
a) No. Of candidate secured more than 48 but not more than 50 marks
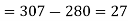
b) No. Of candidate secured less than 48 but not less than 45 marks
Given a set of values of x and y, the process of finding the value of x for a certain value of y is called inverse interpolation.
Lagrange’s Inverse interpolation:
Let 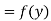 , be defined function we get
, be defined function we get
x |  |  |  | ….. | 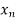 |
f(Y) | 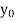 | 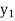 | 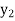 | …… | 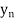 |
Where the interval is not necessarily equal. We assume f(x) is a polynomial of degree n. Then Lagrange’s inverse interpolation formula is given by
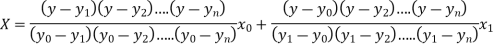

Example1: Use the inverse interpolation to find value of x at 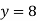 for the following data:
for the following data:
X | 1 | 3 | 4 |
Y | 4 | 12 | 19 |
Here 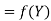 , we have the data
, we have the data
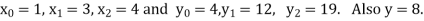
The Lagrange’s inverse interpolation formula is given by
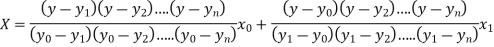
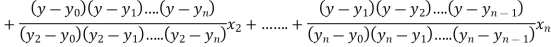
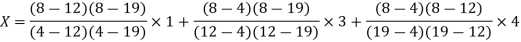
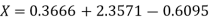
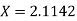 .
.
Example2: Use the inverse Lagrange’s method to find the root of the equation 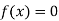 , give data
, give data 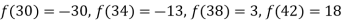
X | 30 | 34 | 38 | 42 |
F(x) | -30 | -13 | 3 | 18 |
Here 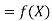 , we have the data
, we have the data

Also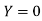 .
.
The Lagrange’s inverse interpolation formula is given by
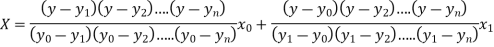
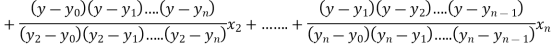
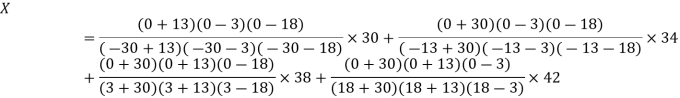
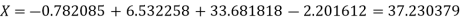
Thus, the approximate root of the given equation is 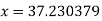 .
.
Example3: Find the value of x at 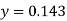 for the following data:
for the following data:
X | 1 | 2 | 4 | 5 | 8 |
Y | 1.000 | 0.500 | 0.250 | 0.200 | 0.125 |
Here 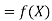 , we have the data
, we have the data
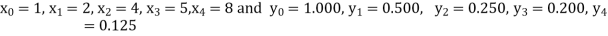
Also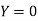 .
.
The Lagrange’s inverse interpolation formula is given by
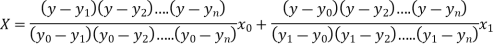
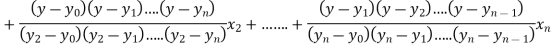


Thus the value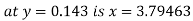
References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port and C. J. Stone, “Introduction to Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction to Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
- T. Veerarajan, “Engineering Mathematics”, Tata McGraw-Hill, New Delhi, 2010
- Higher engineering mathematics, HK Dass
- Higher engineering mathematics, BV Ramana.
- Computer based numerical & statistical techniques, M goyal