Unit – 2
Impulse Water Turbines
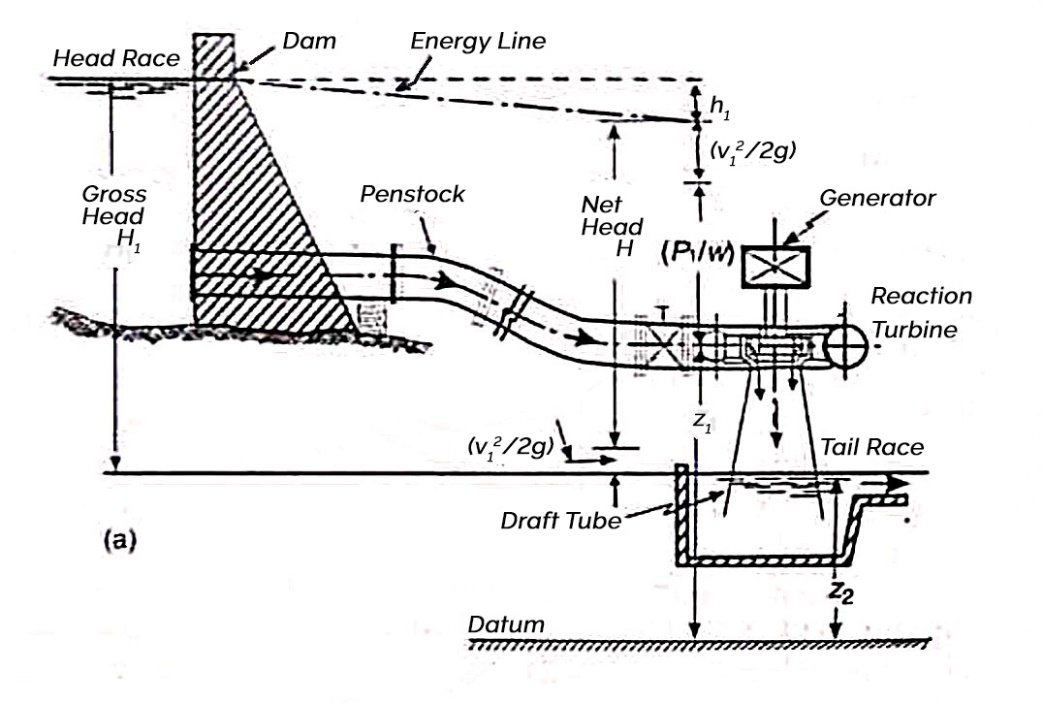
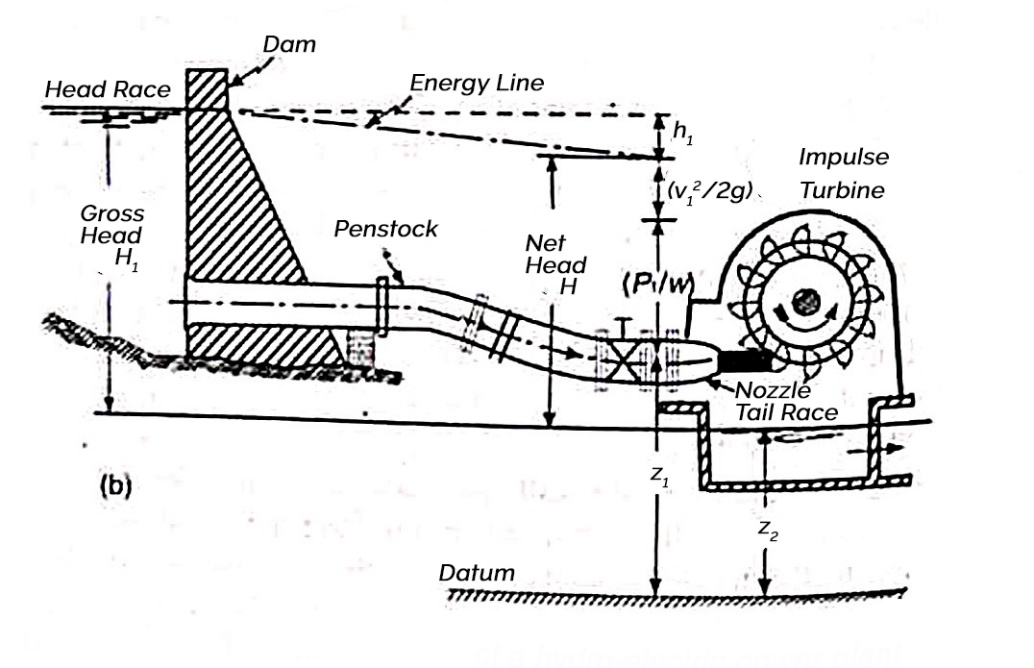
A dam
Penstock
Turbine
Tail race
- impulse turbine
- reaction turbine
- Tangential flow turbine
- Radial flow turbine
- Axial flow turbine
- Mixed flow turbine
- High head turbine
- Medium head turbine
- Low head turbine
- Low specific speed turbine
- Medium specific speed turbine
- High specific speed of turbine
H= Net head acting on the Pelton wheel
= 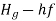
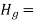 Gross head
Gross head
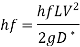
 Dia of penstock
Dia of penstock
N= Speed of the wheel in r.p.m
D= diameter of the wheel
d=diameter of the jet
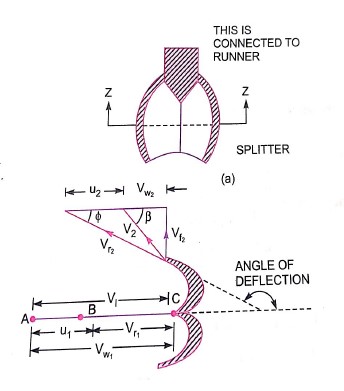
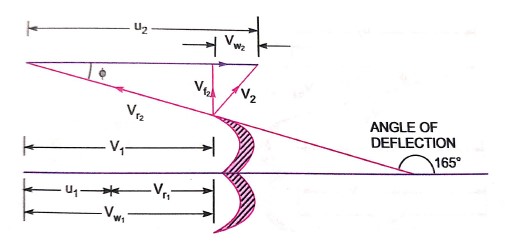
Then, 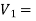 Velocity of jet at inlet
Velocity of jet at inlet

The velocity triangle at inlet will be a straight line where
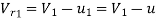
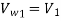
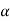 =0 and
=0 and 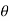 =0
=0
From the velocity triangular at outlet, we have
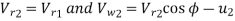
The force exerted by the of water in the direction of motion is given by equation
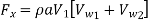
As the angle 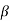 is an acute angle, positive sign should be taken
is an acute angle, positive sign should be taken
a=area of jet 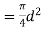
Work done by the jet on the runner per second
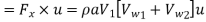
Power given to the runner by the jet
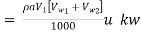
Work done per second per unit weight of water striking
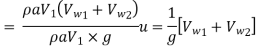
The energy supplied to the jet at inlet is in the form of kinetic energy and is equal to 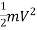
Kinetic energy of jet per second 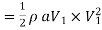
Hydraulic efficiency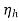
=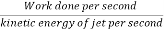

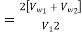 u
u
Now 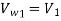
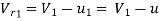

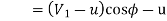

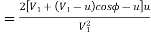
=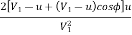

The ideal velocity of jet usually known as spoutting velocity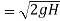
Actual velocity of the jet is slightly less due to friction loss in the nozzle
Thus V = 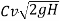
Where, Cv=coefficient of velocity
Velocity of wheel u= 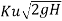
Where Ku = speed ratio
= 0.43 to 0.47
Angle through which jet of water gets deflected in buckets =1650
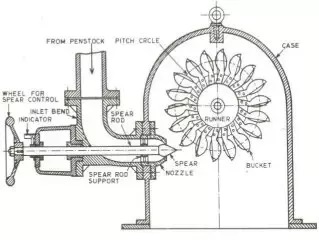
Least diameter d of the jet

Where Q = discharge through jet in 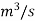
Mean diameter D of Pelton wheel may be obtained as follows
D= 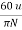
Jet ratio m= 
For maximum efficiency jet ratio should be from 11 to 14
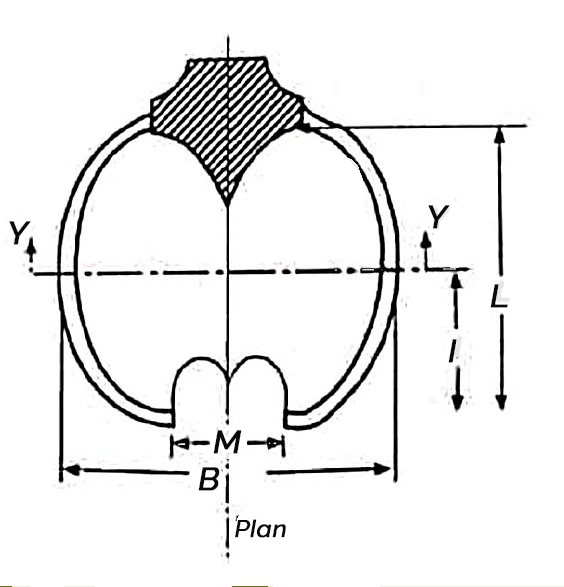
Some of the main dimensions of the bucket of Pelton wheels as shown
B= (4 to 5) d
C= (0.81 to 1.05) d
M=(1.1 to 1.25) d
Angle 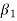 = 5° to 8°
= 5° to 8°
L= (2.4 to 3.2) d
l= (1.2 to 1.9) d
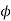 = 10° to 20°
= 10° to 20°
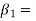 50 to 80
50 to 80
Number of buckets = Z= 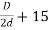
1) Speed (N)
2) Head (H)
3) Discharge (Q)
4) Power (P)
5) Overall efficiency (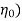
6) Gate opening
Constant head curves
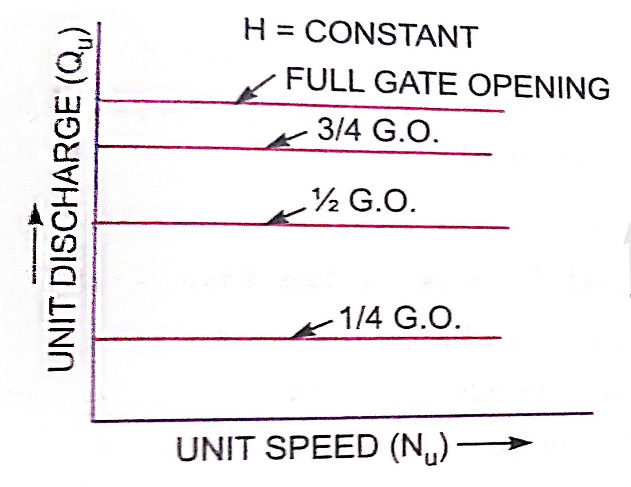
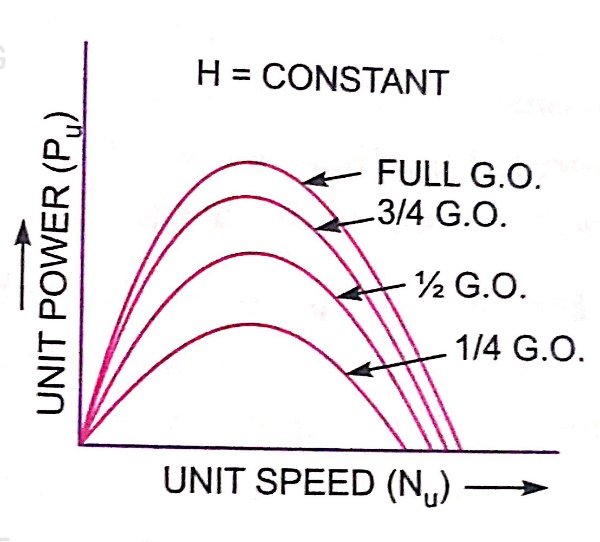
For a Pelton wheel
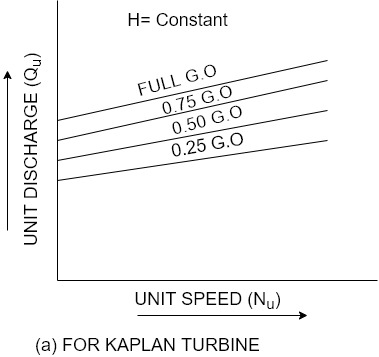

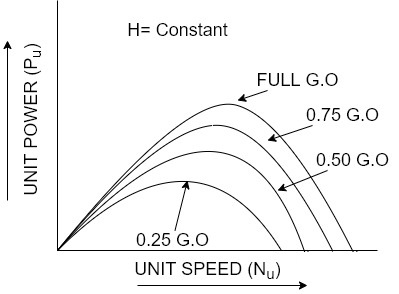
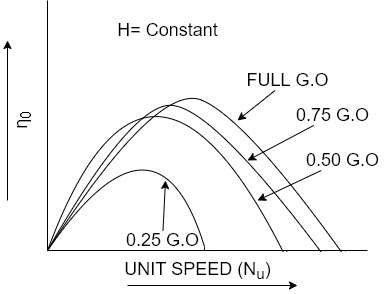
For reaction turbines
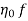

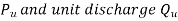
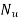
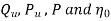
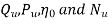
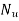
Operating characteristic curves for constant speed curves
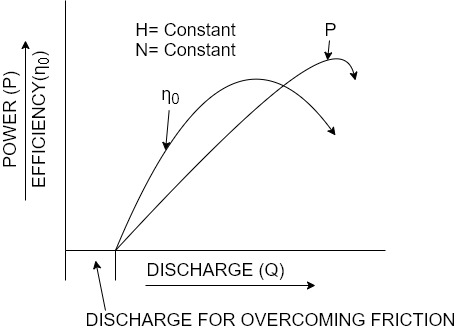
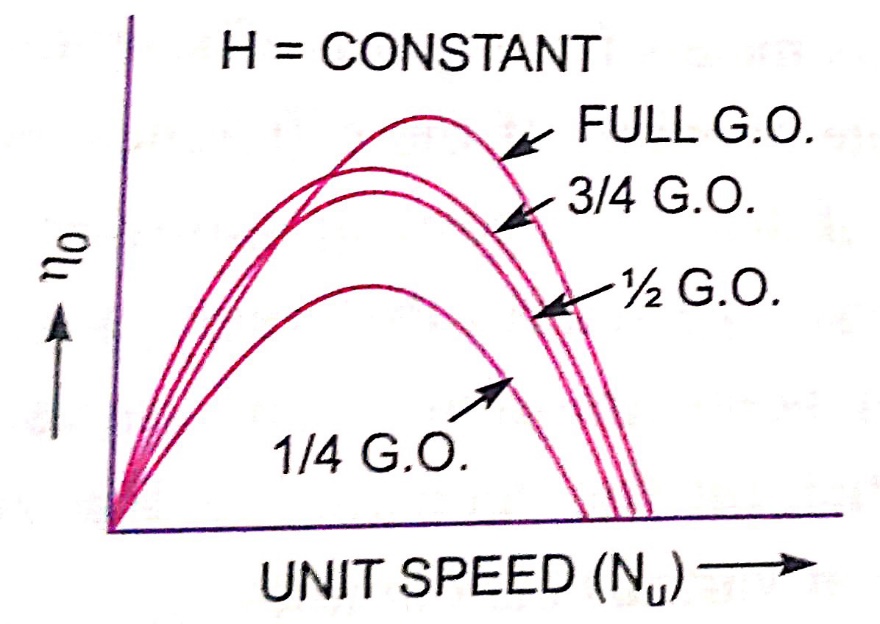
Constant efficiency curves or Muschel curves or iso-efficiency curves


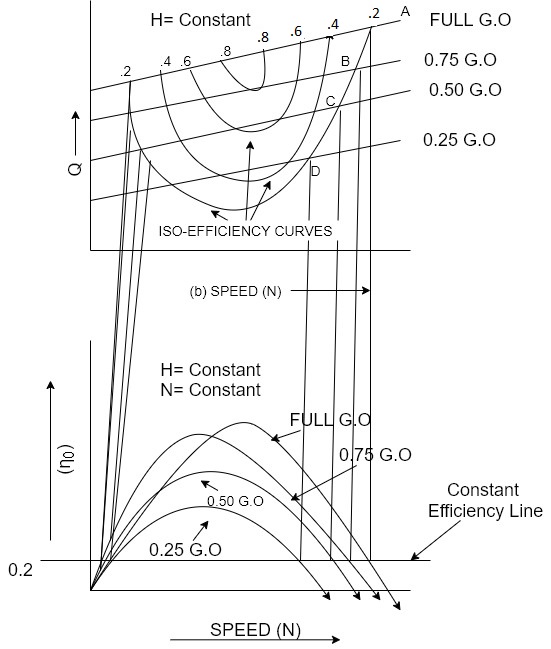
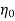
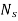
Overall efficiency 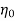 =
=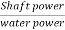
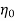 =
= 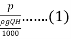
Where H=head under which the turbine is working
Q=discharge through turbines
P=power developed for shaft power
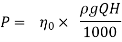
P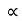 Q× H
Q× H
As 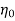 and
and 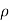 are constant …..(ii)
are constant …..(ii)
D= diameter of actual turbine
N=speed of actual turbine
u=tangential velocity of the turbine
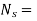 Specific speed of turbine
Specific speed of turbine
V=absolute velocity of water
But. u 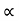 V where V
V where V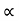 √H
√H
u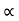 √H (iii)
√H (iii)
But. u=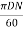
u DN….(iv)
DN….(iv)
From equation (iii) and (iv)
√H. 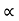 DN
DN
Or D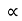

Discharge Q= A×V
A 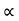 B×D
B×D
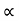
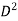
V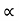 √H
√H
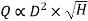
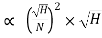
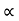
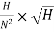
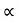
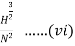
Put the value of Q in equation (ii)
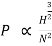 ×H
×H
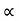

P=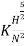
where K=constant of proportionality
If P=1 and H=1 Speed N=Specific speed
Put these values in above equation

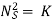
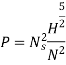
Or 

Significance:-
Following factors are considered for selecting a particular turbine at place
1) Head:- The net head under which the turbine is working plays an important role for selecting turbine.
The type of turbine for different heads
Net head in m | Types of turbine |
300m or more | Pelton turbine |
150m to 300m | Pelton or Francis |
50m to 150m | Francis turbine |
Less than 50 m | Kaplan or propeller |
2) Specific speed :- The specific speed is also an important factor for deciding the type of turbine to be installed at a place.
Specific speeds | Types of turbines |
85 to 30 | Pelton wheel with single jet |
31 to 50 | Pelton wheel with double jet |
51 to 225 | Francis |
256 to 860 | Kaplan or propeller |
3) Part load operation :-
4) overall cost of installation and cavitation characteristics :-
Numericals :
1. A Pelton turbine develops 3000 kW power under the head of 300 m. The overall efficiency of the turbine is 83%. If the ratio is 0.46 coefficients of nozzles 
i) diameter of the turbine
ii) Diameter of the jet
P=3000 kW
H=300m
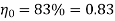
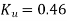
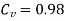
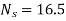
Find D and d.
Sol. 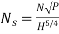
16.5= 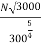
N= 376.11 r.p.m
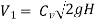
= 0.98×√2×9.81×300
= 75.18 m/s
u=Ku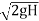
= 0.45×√2×9.81×300
=34.52 m/s

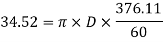
D=1.75 m
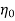 =
= 
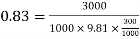
Q=1.228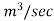
Q = A×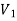
1.228 = 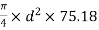
d=0.144 m
2. The mean bucket speed of a Pelton wheel is 40 m/s and discharge is 1.2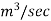 The head over the turbine is 385 m. The head loss due to friction in penstock is 9 m. The bucket deflects the jet through 165°. If coefficient of velocity of nozzle is 0.9, determine
The head over the turbine is 385 m. The head loss due to friction in penstock is 9 m. The bucket deflects the jet through 165°. If coefficient of velocity of nozzle is 0.9, determine
i) Power developed by the turbine
ii) Hydraulic efficiency of turbine neglect bucket friction.
Sol.
u=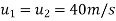
Q= 1.2
Hg=385m
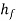 = 9m
= 9m
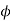 = 180-165=15°
= 180-165=15°
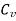 =0.9
=0.9
Net head available = H = 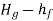
= 385 - 9
= 376 m
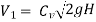
=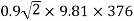
= 77.30m/s
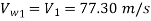
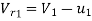
= 77.30-40
= 37.30 m/s
 37.30 m/s
37.30 m/s
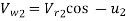
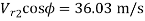
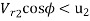
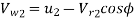
=40 - 36.03
= 3.97 m/s
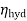 =
= u
u
=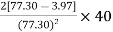
=0.9817
=98.17%
Power developed = 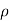 Q
Q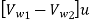
=1000×1.2[77.30-3.97]
=3.52×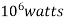
=3520 KW
3. A Pelton wheel is working under a head at 300m and mean bucket speed of 10m/s. Discharge through the turbine is 700 lit/sec. The buckets deflect the jet through an angle of 160°. Calculate power given by water to the runner and hydraulic efficiency of the turbine. Assume coefficient of velocity as also calculate overall efficiency and shaft power if mechanical efficiency is 85%.
Sol. H=300m
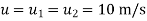
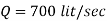
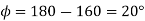

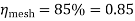

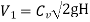
= 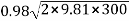
= 75.18m/s
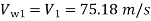
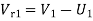
= 75.18 - 10
= 65.18m/s
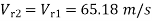
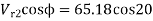
= 61.25m/s
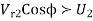
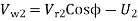
= 61.25 - 10
= 51.25m/s
Power given by water to the runner
(Runner power)=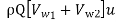
=1000 x 0.7 [75.18 + 51.25] x 10
= 885.01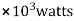
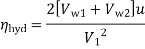
=
= 0.4473
= 44.73%
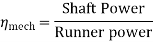
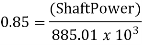
Shaft power = 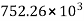 watts
watts
Overall efficiency=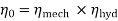
= 0.85  0.44
0.44
= 0.374
=37.4%
Ques
4. A Pelton wheel is to be designed for a head of 60m when running at 200 rpm . The Pelton wheel develops 95.6475 KW Shaft power the velocity of buckets =0.45 times the velocity of the jet , overall efficiency = 0.85 & coefficient of the velocity is equal to 0.98.
Solution
H=60m
N=200m
S.P.= 95.6475 KW
u = 0.45 V
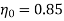
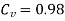
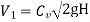
= 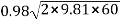
= 33.62m/s
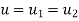 = 0.45 V
= 0.45 V
= 0.45 x 33.62
=15.13m/s
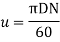
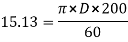
D=1.44m
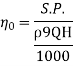
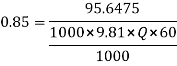
Q=0.1912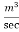
Q=A x 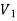
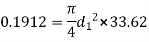
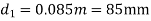
Width of buckets=5d=5 x 85
=425mm
Depth of buckets=1.2d=1.2 x 85
=102mm
Number of buckets=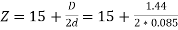
= 23.5 = 24
Reference:
1. Fluid Mechanics & Hydraulics Machines- R.K. Bansal
2. Hydraulics & Fluid Mechanics – Modi & Seth