Unit 6
Impact and collision
Introduction:-
We have seen that if a glass ball is allowed to fall on marble floor from certain height it rebounds i.e. rises up after striking the floor. To certain height we observe that rebound height is always less than height from it dropped. If same ball is dropped on wooden floor from same height it will rebound but rebound height much lesser than height observed for marble floor. We will see that if base of different materials are allowed to fall on marble floor they will rebound two different heights. This property of bodies by virtue of which they rebound after impact is called elasticity. The body which rebound to greater height is said to be more elastic than that which rebound to lesser height. But if a body does not rebound at all after impact it is called on inelastic body.
Whenever two elastic bodies collide with each other they tend to compress each other, they tend to compress each other. Immediately after this two bodies attempt to regain its original shape due to their elasticity. This process of regaining original shape is called restitution.
Some definitions
Time of compression
The time taken by two bodies in compression after the instant of collision is known as time of compression.
Time of restitution
The time taken by two bodies to regain the original shape after compression is known as time of restitution.
Time of collision
The sum of time of compression and time of restitution is known as time of collision or period of collision or period of impact.
Law of conservation of momentum
It states that, “The total momentum of two bodies remains constant after their collision or any other mutual action.”
Mathematically,
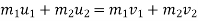
Where
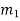=mass of first body
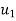=initial velocity of first body
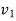=final velocity of first body
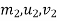=corresponding values for second body.
Newton's law of collision of elastic bodies
Its state,” when two moving bodies collide with each other, their velocity of separation there's a constant ratio to their velocity of approach.”
Mathematically,
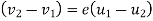
Where,
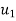=initial velocity of first body
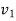=final velocity of first body
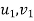=corresponding values for second body
e=constant of proportionality, also known as coefficient of restitution.
Coefficient of restitution:-
It is defined as the ratio of velocity of separation (of to moving bodies collide with each other) to their velocity of approach.
It is also defined as the ratio of relative velocities of colliding bodies after impact to their relative velocity before impact.
It is denoted by symbol 'e'
The relative velocities are measured along the line of impact which is the common normal to colliding surfaces.
Consider two bodies A and B having direct impact as shown in figure 1
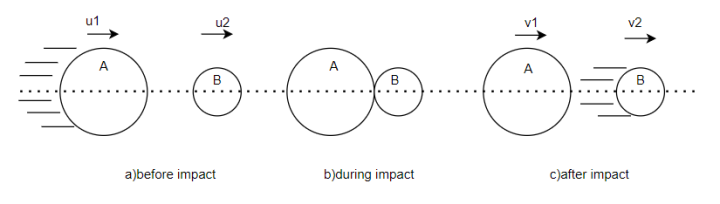
Let,
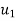=initial velocity of body A
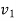=final velocity of body A
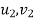=corresponding values for body B
The impact will take place only if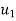 
is greater than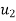 
Velocity of approach=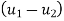
After impact separation will take place only if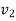 
is greater than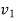 
Velocity of separation=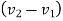
According to Newton’s law of origin for elastic bodies
Velocity of separation=e× velocity of approach
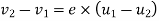
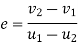
Where
e=constant of proportionality and is called coefficient of restitution
Its value lies between 0 and 1
If e=0 => two bodies are inelastic
If e=1 => two bodies are perfectly elastic
Notes:-
1) The velocity of approach or separation of two bodies which are moving in same direction before or after impact is difference of their velocities.
2) For the two bodies moving in opposite direction the velocity of approach or separation is some of their velocities.
Type of impacts:-
Impact means the collision of two bodies which occurs in very small interval of time and during which two bodies exert very large force on each other.
Types of impacts are
1) Direct impact
2) Indirect impact oblique impact
Direct impact:-
The line of impact of two colliding bodies is the line joining the centres of these bodies and passes through the point of contact as point of collision as shown in figure 2
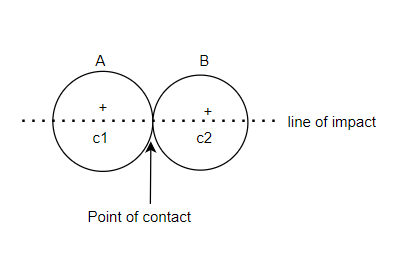
Now consider two bodies A and B having direct impact as shown in figure 2
Let
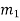=mass of first body
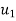=initial velocity of first body
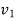=final velocity of first body
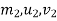=corresponding values for second body
According to law of conservation of momentum
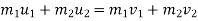
Note:-
1) Since the velocity is vector quantity, therefore the direction should always be kept in view while solving examples
2) If one of the body is initially at rest then such collision is also called impact.
Example 6:- Ball A of mass 1 kg moving with velocity 2m/s strikes directly on ball B of mass 2 kg at rest. Ball A after striking comes to rest. Find velocity of ball B after striking and coefficient of restitution.
Solution:- given
Mass of ball A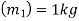 
Mass of ball B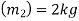 
Initial velocity of ball A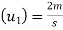 
Initial velocity of ball B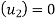 
Final velocity of ball A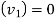 
This is the case of direct impact
According to law of conservation of momentum
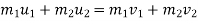
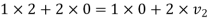
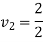
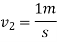
Coefficient of restitution=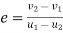
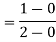
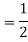
Example 2:- A ball of mass 20 kg moving with velocity of 5m/s strikes directly another ball of mass 10kg moving in opposite direction on with velocity 10m/s. If coefficient of restitution is equal to 5/6 then determine velocity of each ball after impact.
Solution:- given
Mass of first ball A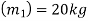 
Mass of second ball B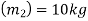 
Initial velocity of first ball A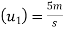 
Initial velocity of second ball B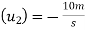 
-ve sign due to opposite direction
According to law of conservation of momentum
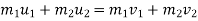
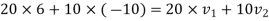
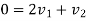
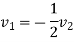
Also
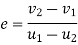
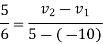
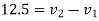
But
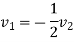
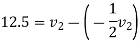
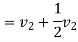
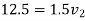
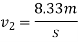
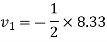
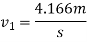
Example 3:- Three perfectly elastic balls A,B and C of masses 2kg,6kg and 12kg respectively are moving in same direction with velocities 12m/s,4m/s and 2m/s respectively. If ball A strikes with ball B, which interns strike with ball C, prove that the balls A and B will be brought to rest by impact.
Solution:- Given
For perfectly elastic balls e=1
Mass of first ball A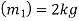 
Mass of second ball B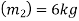 
Mass of third ball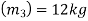 
Initial velocity of first ball A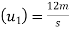 
Initial velocity of second ball B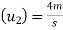 
Initial velocity of third ball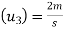 
a) Consider impact of first and second ball according to law of conservation of momentum
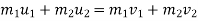
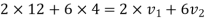
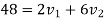
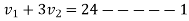
Also
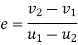
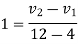
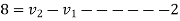
1+2
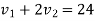
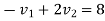
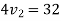
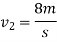
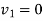
Velocity of ball A after striking is zero.
I.e. ball A brought to rest by impact A &B
b) consider impact of ball B and ball C
As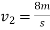 
for impact of ball A and ball B
Initial velocity of ball=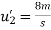
Applying law of conservation of momentum
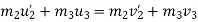
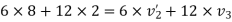
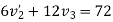
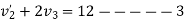
Also
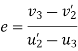
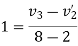
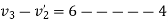
3+4
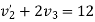
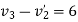
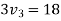
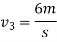
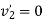
Hence velocity of second ball after impact with third ball is zero.
Hence second ball brought to rest after impact with third ball C.
In a direct impact of two bodies
If two bodies before impact are not moving along the line of impact the collision is called indirect (or oblique) impact. As shown in figure 3
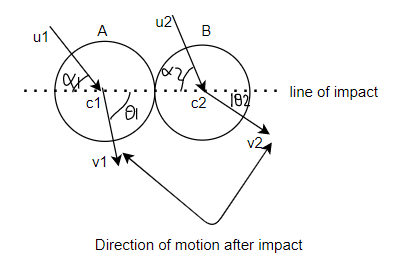
Consider two bodies A and B having an indirect impact as shown in figure 3
Let
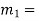mass of first body
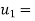initial velocity of first body
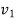=final velocity of first body
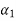=Angle which initial velocity of first body makes with the line of impact.
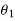=Angle which final velocity of first body makes with the line of impact.
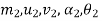=corresponding values for second body
The components of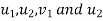 
along line of impact will cause the direct impact and all relation for direct impact will hold good for this component. Other components of 
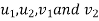(i.e. along the perpendicular to line of impact) will not affect the phenomenon of impact in anyway and component of initial velocity will be equal to component of final velocity of body.
Now,
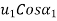=component of initial velocity along the line of impact for first body
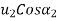=Component of initial velocity along the line of impact for second body
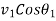=Component of final velocity along the line of impact for first body
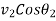=Component of final velocity along the line of impact for second body
Now,
The law of conservation of momentum, the total initial momentum in any direction must be equal to final momentum in that direction.
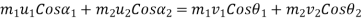
The Newton's law of collision of elastic bodies also hold good for indirect impact.
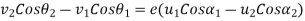
Direct impact of a body on a fixed plane
Consider a fixed plane which is at rest before impact and after impact. Consider a body having direct impact on fixed plane.
Let
u=initial velocity of the body
v=final velocity of the body
e=coefficient of restitution
Velocity of approach between body and fixed plane=initial velocity of body-final velocity of plane
=u-0
=u
Velocity of separation between body and fixed plane
=Final velocity of body-final velocity of plane
=v-0
=v
Coefficient of restitution is given by
e=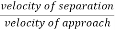
e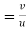
Important cases:-
A body is falling from some height
Let
H=height from which body is falling
u=velocity with which body strikes the floor
This velocity will be obtained by using the equation
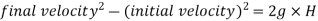
Initial velocity=0
Final velocity=u
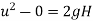
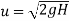
b) A body is projected upward initially and then strike the floor
When body is projected upwards with some initial velocity, the body will reach the greatest height and then will return to ground with same velocity with which it was projected.
Example 4:- from a point, on a smooth floor of a room a toy ball is a shot to hit a wall. The ball then returns back to point of projection. If time taken by ball in returning is twice the time taken in reaching the wall. Find the coefficient of restitution between ball and wall.
Solution:- given
Let s=distance point of shot and wall
t=time taken by ball to reach the wall
Time taken by ball to return point of shot=2t
e=coefficient of restriction between ball and wall
We know,
Velocity of ball with which it hits the wall=s/t
Velocity of ball with which return to the point of shot=s/2t
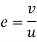
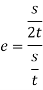
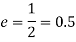
Example 5:- A ball is dropped from height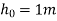 
on a smooth floor, knowing that the height of first bounce is 
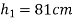determine
a) Coefficient of restitution (e)
b) Expected height 
second bounce
Solution:- given
Height from which ball is dropped=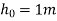
Height after first bounce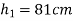 
=0.81m
a) Coefficient of restitution
We know velocity with which ball impinges on floor
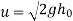
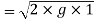
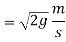
Velocity with which ball bound
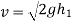
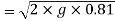
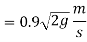
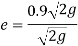
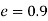
b) Expected height after 2nd bounce
Let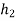 
=height after 2nd bounce
The velocity with which the ball impinges second time is same with which ball rebounded first time
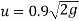
And velocity with which ball rebounds
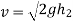
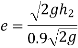
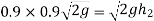
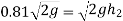
Squaring on both sides
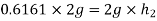
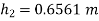
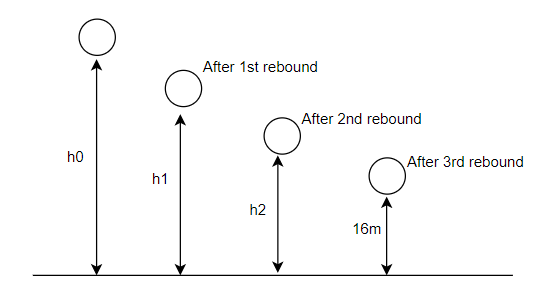
Example 6:- from what height, master heavy elastic ball be dropped on a floor so that after rebounding thrice it will reach a height of 16 metres take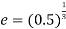 
Solution:- consider the following figure 4
Let
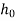=height from which ball is dropped
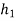=height after 1st rebound
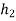=height after 2nd rebound
We know,
The velocity with which ball impinges on floor
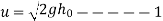
Velocity with which ball rebound first time
Similarly velocity with which ball impinges after first rebound
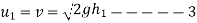
Velocity with which ball rebound second time
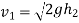
Velocity with which ball impinges after second rebound
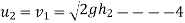
Velocity with which ball rebound third time
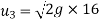
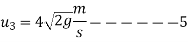
We know that during first impact
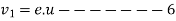
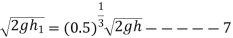
Similarly during second impact
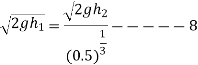
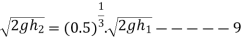
And during third impact
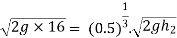
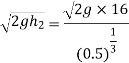
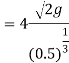
Now substituting value of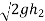 
in equation 8
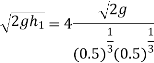
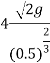
Now substituting value of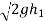 
in equation 7
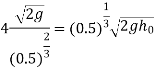
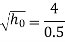
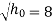
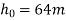
Reference Books
1.Engineering Mechanics by S. S. Bhavikattis, New Age International Pvt. Ltd.
2.Engineering Mechanics by R. K. Bansal and Sanjay Bansal.
3.Vector Mechanics for Engineers Vol.I and II by F. P. Beer and E. R. Johnston, Tata Mc-Graw Hill Publication.
4.Engineering Mechanics by Manoj K Harbola, Cengage Learning
5.Engineering Mechanics by K. I. Kumar, Tata Mc-Graw Hill Publication
6.Engineering Mechanics by S. B. Junnerkar.
7.Engineering Mechanics by Irving H. Shames, Prentice Hall of India, New Delhi.
8.Applied Mechanics by S. N. Saluja, Satya Prakashan, New Delhi.
9.Engineering Mechanics by Statics and Dynamics by Ferdinand Singer, Harper and Row Publications
10.Engineering Mechanics by R. S. Khurmi, S. Chand Publications
11.Fundamentals of Engineering Mechanics by S. Rajasekaran, G. Sankarasubramanian,VikasPublishing House
12) “Applied Mechanics- Dynamics &Statics ” by I.B.Prasad, Khanna Publisher, Delhi
