Unit - 1

Matrices and Solution of Linear System Equations

1.1           Rank of matrix: definition, normal form and echelon form

The rank of a matrix is the largest order of the non zero minor of the matrix( we search at least one non zero minor  to find the rank of the matrix).

A matrix A is said to have the rank r if and only if there exist at least one non zero minor of the given matrix of order r and every minor greater than order r is zero.

This is denoted by .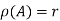

Normal form of a matrix:

Every non singular matrix A of rank r can be converted by applying sequence of the elementary transformation in the form of

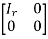
Is called the normal form of the matrix A.

Also the rank of a matrix can be calculated by converting it into normal form then the order of identity matrix obtained is the rank of the given matrix.

Example1: Reduce the following matrix into normal form and find its rank,

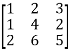
Let A =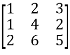

Apply 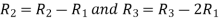we get

A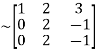 

Apply we get

A 

Apply

A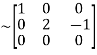 

Apply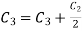

A 

Apply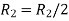 

A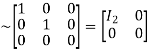 

Hence the rank of matrix A is 2 i.e. .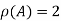

Example2: Reduce the following matrix into normal form and find its rank,

Let A =   

Apply 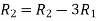and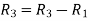

A

Apply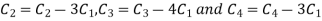

A

Apply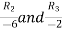

A

Apply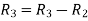

A

Apply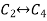

A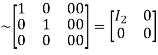

Hence the rank of the matrix A is 2 i.e. .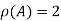

Example3: Reduce the following matrix into normal form and find its rank,

Let A =

Apply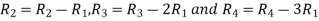

Apply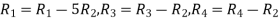

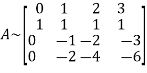
Apply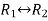

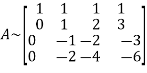
Apply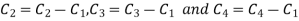 

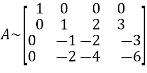
Apply 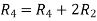and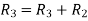

Apply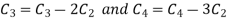

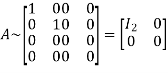
Hence the rank of matrix A is 2 i.e. .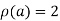

1.2           Consistency of linear system equations

A consistent linear system is a system of linear equations with at least one set of values satisfying all equations.

Explanation:

A system of linear equations is said to be consistent if there is a solution which satisfies all of the equations.

Example 1:

x+ y =1

x+2y=5 has the solution

x=−3; y=4 and thus is consistent.

The system

x+ y =12

x+2y=2 has infinitely many solutions, as any (x, y) pair will work so long as y=−x+1. As such, it is also a consistent system.

However, the following system is not consistent

x+ y= 1

x+ y =2 as there is clearly no pair of values (x, y) which fulfil both equations.

In other words, we can further classify consistent system of linear equation as following.,

Two or more linear equations are said to be consistent if they have same variables.

For example,

X+2y=14 & 2x+y=6 is said to consistent system of linear equations.

The system of linear equations is said to be consistent if have at least one solution in common.

Example 2:

X+y-6=0 &x-y-2=0 is consistent as the have one solution in common.

Example 3:

X=12-y & 3y-x=0 is also said to be consistent system of linear equations.

*A two-variable system of equations said to be consistent if the lines formed by equation are equal or parallel.

*A three-variable system of equations are said to be consistent if they have the following.,

1.All the three planes should be parallel.

2.Any two of the planes are parallel, and the third should meet at one point of the two planes and the other at some point.

1.3           System of linear homogeneous equations

The standard form of system of homogenous linear equation is

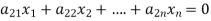                 (1)

…………………………………

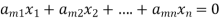
It has m number of equations and n number of unknowns.

Let   the coefficient matrix be A =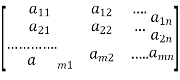

By elementary transformation we reduce the matrix A in triangular form we calculate the rank of matrix A, let rank of matrix A be r.

The following condition helps us to know the solution (if exists consistent otherwise inconsistent) of system of above equations:

1. If r =  n i.e. rank  of coefficient matrix is equal to number of unknowns then system of  equations has trivial zero  solution by

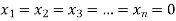
II.                 If   r < n i.e. rank of coefficient matrix is less than the number of unknowns then system of equations has (n-r) linearly independent solutions.

In this case we assume the value of (n-r) variables and other are expressed in terms   of these assumed variables. The system   has infinite number of solutions.

III.               If m < n i.e. number of equations is less than the number of unknowns then system of equations has non zero and infinite number of   solutions.

IV.              If   m=n number of equations is equal to the number of unknowns then system of equations has non zero unique solution if and only if |A|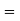0. The solution is consistent. The |A| is called eliminant of equations.

Example1: Solve the equations:

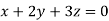
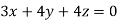
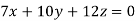
Let the coefficient matrix be A =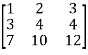  

Apply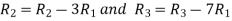

A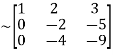

Apply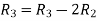 

A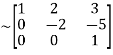

Since |A| ,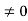 

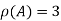
Also number of equation is m=3 and number of unknowns n=3

Since rank of coefficient matrix A = n number of unknowns

The system of equation   is consistent and has trivial zero solution.

That is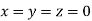  

Example2: Solve completely the system of equations

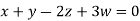
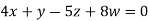
Solution: We can write the given system of equation as AX=0

Or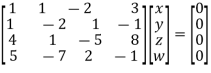

Where coefficient   matrix A  =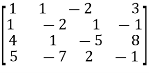

Apply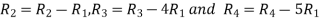 

A  

Apply

A 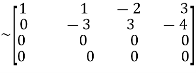       …(i)

Since  |A|=0   and  also 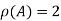, number of  equations m =4  and   number  of unknowns  n=4.

Here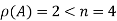 

So that the system has (n-r) linearly independent solution.

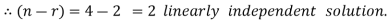
Let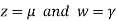

Then from equation (i) we get

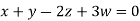
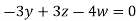
Putting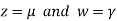 

We get 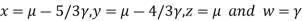  has infinite   number solution.

Example 3: find the value of λ for which the equations

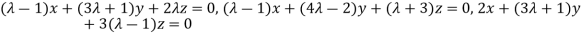
Are consistent, and find the ratio of x: y: z when λ has the smallest of these values. What happen when λ has the greatest o these values?

The system of equation is consistent only if the determinant of coefficient matrix is zero.

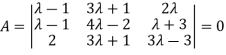
Apply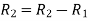

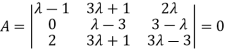
Apply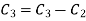 

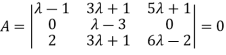
Or 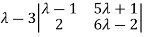=0

Or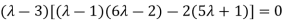

Or (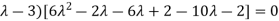

Or (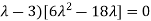

Or 

Or 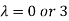………….(i)

1. When λ =0, the  equation become 

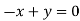
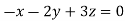
3z=0

On solving we get

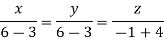
Hence x=y=z

II.                 When λ=3, equation become identical.

1.4 System of linear Non-homogeneous equations

The standard form of system of non- homogenous linear equation is

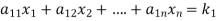
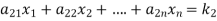                (1)

…………………………………

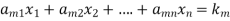
It has m number of equations and n number of unknowns.

Let   the coefficient matrix be A =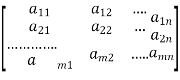

And the augmented matrix   be K =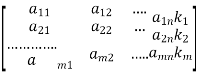

By elementary transformation we reduce the matrix A   and K in triangular form we calculate the rank of matrix A and K. 

Roache’s Theorem: The  system of equations(1)  is  consistent  if  and  only  if the coefficient matrix A and  the augmented  matrix K are the  same  rank otherwise  the  system  is inconsistent.

The following condition helps us to know the solution (if exists consistent otherwise inconsistent) of system of above equations:

Let the   rank   of matrix A is r and matrix K   is r’, number   of equations be   m and number   of   unknowns be n.

1. If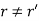, then system of   equations   is inconsistent i.e.  has no solution.
2. If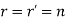, then system of   equations   is consistent i.e.  has unique solution.
3. If, then system of   equations   is consistent i.e.  has infinite number solution.  It has (n-r) linearly   independent solutions i.e.  we  assume arbitrary  values  for (n-r)  variable  and  rest variable  are  expressed  in  terms  of  these.

Example1:  Solve the system of equations:

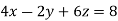
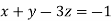
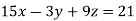
We can write the system as

Apply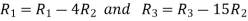

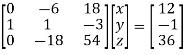
Apply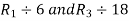

Apply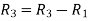 

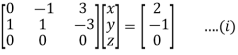
Here coefficient matrix A=  then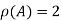 

And augmented matrix K= 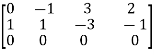 then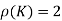 

Since rank of coefficient matrix and   augmented matrix are equal   and is less than the number of unknowns. Therefore system have (n-r) =3-2=1, linearly independent solutions.

From equation (i) we have

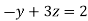
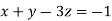
Let 

So,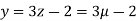

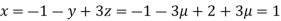
Hence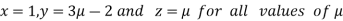 

Hence system   has infinite   number of solutions.

Example2: Investigate for what value of λ and µ the simultaneous equations:

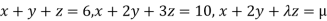
Have (i) no solution

(ii) Unique solution

(iii) An infinite number of solutions.

We can write the given system as

Apply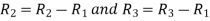

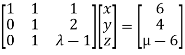
Apply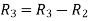

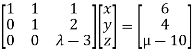
Here the coefficient matrix is A= 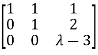and augmented matrix K=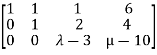

1. The system has no solution if rank of coefficient matrix is not equal to rank of augmented matrix. This is possible only if .

So, λ=3 and µ≠10 in case of no solution.

II.                 In case of unique solution we have rank of coefficient matrix, augmented matrix and number of unknowns must be equal.

This is possible only if 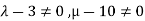as n=3

This implies that 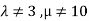  for unique solution.

III.               In case of infinite solution we have rank of coefficient matrix, augmented matrix are equal but less than number of unknowns

This is possible only if 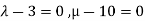as n=3.

This implies that 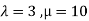  for infinite solution.

Example3: Find the values of a and b for which the equations

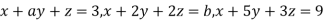
Are consistent. When will these equations have a unique solution?

We can write the above system as

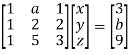
Apply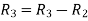

Apply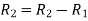

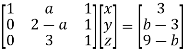
Apply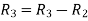

Here the coefficient matrix is A =

And augmented matrix K is

1. The system has no solution if rank of coefficient matrix is not equal to rank of augmented matrix. This is possible only if .

So, a=-1 and b≠6 in case of no solution

II.                 In case of unique solution we have rank of coefficient matrix, augmented matrix and number of unknowns must be equal.

This is possible only if

So, 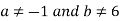  for unique solution.

III.               In case of infinite solution we have rank of coefficient matrix, augmented matrix are equal but less than number of unknowns

This is possible only if 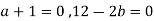as n=3.

This implies that   for infinite solution.

Reference Books:

1. Advanced Engineering Mathematics by Erwin Kreyszig, Wiley India Pvt. Ltd.

2. Advanced Engineering Mathematics by H. K. Dass, S. Chand, New Delhi.

3. A text book of Engineering Mathematics Volume I by Peter V. O’Neil and Santosh K.Sengar,Cengage Learning.

4. Mathematical methods of Science and Engineering by Kanti B. Datta, Cengage Learning.

5. Numerical methods by Dr. B. S. Grewal, Khanna Publishers, Delhi.

6. A text book of Engineering Mathematics by N. P. Bali, Iyengar, Laxmi Publications (P) Ltd.,NewDelhi.